博斯腾湖西岸湖滨绿洲土壤含盐量高光谱估算*

赵慧，李新国，靳万贵，麦麦提吐尔逊·艾则孜，牛芳鹏

（新疆师范大学地理科学与旅游学院/新疆干旱区湖泊环境与资源实验室，新疆乌鲁木齐830054）

土壤盐分在土壤中的含量决定了土壤盐渍化等级，土壤含盐量过高，会危害农作物减产或绝收、影响植被生长并间接造成生态环境恶化［1-3］。快速、准确地获取土壤盐分信息在土壤开发利用和土壤盐渍化防治等方面具有重要的意义［4］。传统土壤含盐量的测定需要耗费时间，且步骤繁琐，对大面积土壤盐分进行持续性和稳定性的动态检测比较困难，而高光谱遥感技术的出现成为估算土壤盐分强有力的工具，可以充分挖掘光谱信息和构建高精度的模型［5-7］。光谱一、二阶微分在进行土壤含盐量光谱建模中是一种常用的光谱数据预处理方法［8-9］。但一阶微分和二阶微分的光谱曲线中间相差较多，导致一些中间的光谱信息会被遗漏掉，而分数阶微分可以挖掘中间的光谱信息，能够使光谱信息被充分利用，且分数阶微分在模式识别和建模等方面被广泛应用［10-12］。亚森江·喀哈尔等［13］采用分数阶微分优化光谱指数的方式，认为1.6阶微分波段预测效果最佳，精度达到0.84。吾木提·艾山江等［14］通过高光谱估算含水量，分析到分数阶微分后的模型能够提高稳定性和预测能力。蒋明等［15］提出在不同采样间隔下分数阶微分对土壤重金属的影响。分数阶微分能够细化相关系数的趋势，丰富光谱数据的处理方式［16-18］。分数阶微分在高光谱预处理中，能够增加特征波段的数量，但对于有效地提高相关性还处于弱势，因此本文将分数阶微分与传统的数学光谱变换相结合，以提高相关性。基于此，以博斯腾湖西岸湖滨绿洲的土壤含盐量为研究对象，将分数阶微分引入高光谱数据预处理中，且对原始光谱曲线进行数学变化的基础上，利用偏最小二乘回归建模，比较原始光谱曲线及4种光谱变换的分数阶微分建模精度。

1 材料与方法

1.1 研究区概况

博斯腾湖西岸湖滨绿洲行政区划隶属于新疆博湖县，位于新疆焉耆盆地东南部，地理位置介于86°15′～86°55′E，41°45′～42°10′N。其是典型的人工绿洲和自然绿洲混合的山前湖泊绿洲，面积为1 360 km2。年平均气温8.2～11.5 ℃，无霜期175.8～211.3 d，年蒸发量1 880.0～2 785.8 mm，年降水量47.7～68.1 mm，蒸降比高达40∶1。研究区内土壤类型主要有草甸土、沼泽地、灌耕潮土、盐土、风沙土、棕漠土等，地下水埋深1.0～2.5 m，矿化度为0.1～10 g/L［19］。植物类型有芦苇（Phragmites australis）、柽 柳（Tamarix ramosissi⁃ma）、杨树（Populus），农作物有辣椒地（Capsi⁃cum field）、油葵地（oil sunflower field），以及裸地（Bare field）等。由于独特的地理位置，且蒸发强烈，降水稀少等气候条件，活跃的地表水以及地下水补给，富含盐分的母质环境等，平均土壤盐分含量为2.84 g/kg［20］。

1.2 土壤样品采集及测定

根据研究区土壤类型的现状，结合研究区的土壤盐分状况，采用GPS 定位技术，使采样点尽可能遍及研究区范围内的主要土地利用类型，考虑采样点的水文地貌条件、植被覆盖类型以及土壤盐渍化程度等因素，每个样本点范围分0～10 cm 深度进行，共采集37 个样点（图1）。将土壤样品带回实验室经过前期处理自然风干后除去枯枝、残叶等杂质，磨碎过2 mm 网筛后，分装自封袋中用于后续土壤含盐量测定和光谱采集。从37 个代表性的土壤样品中随机选取25个样本作为建模集，剩下的作为验证集，建模集和验证集的平均值分别为2.64、2.86。

土壤光谱测定采用ASD FieldSpec3 型光谱仪，波段范围为350～2 500 nm，重采样间隔为1 nm。每次采集回来之后的土壤样品预处理之后，尽快测量土壤光谱。野外测量需要选择晴朗无风的天气，测量时间为12：00～14：00，测定之前先进行白板校正，校正间隔控制在3～5 min，测定时始终保证传感器探头位于土面正上方15 cm处［21］，每个土壤样品重复测量15 条光谱曲线，取其平均值作为此样本的光谱数据。

图1 采样点及研究区示意图Fig.1 Sampling point and location of the study area

1.3 数据处理与研究方法

1）对均值处理后的光谱曲线去除水分吸收带波段1 340～1 450 nm、1 750～2 020nm、2 330～2 500 nm［22］，对去除干扰波段的光谱曲线用Savitz⁃ky-Golay滤波方法进行平滑处理。

2）分数阶微分是将整数阶微分的阶数扩展至任意阶［23］。目前，Grünwald-Letnikov［24-25］定义的分数阶微分较为常用，主要是应用一元函数差分来实现，表达式为：

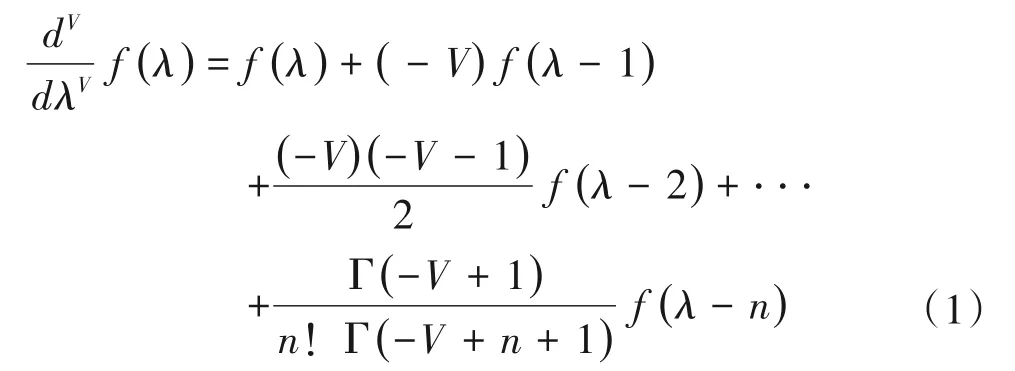
式中，V-阶数，Γ(⋅)-Gamma 函数，λ-对应的值，n-是微分上下限之差。

在平滑后的原始光谱曲线R的基础上，对均方根 R、对数lg R、倒数1/R、对数倒数1/lgR 进行变换，再利用（1）式分别对原始光谱曲线R 及4种变换进行0～2 阶的分数阶微分处理（阶数间隔为0.2）。

3）采用偏最小二乘回归（PLSR）方法进行建模及验证，PLSR 方法融合主成分分析、典型相关分析和多元线性回归分析［26-27］。在多元线性回归里采用逐步回归，逐步分解输入变量矩阵和输出变量矩阵，并综合考虑提取的主成分对输入变量矩阵和输出变量矩阵的解释能力，直到满足性能要求为止。建模和验证的精度分别用决定系数R2C、，均方根误差RMSEC、RMSEV［28］。R2用来判定建模的稳定程度，越接近1 说明模型越稳定；RMSE 用来说明模型的准确度，值越小表示模型的精度越高［29］。

2 结果与分析

2.1 土壤含盐量高光谱特征

对土壤含盐量光谱反射率进行聚类分析，以K-means 聚类算法进行划分。由图2 所示，利用聚类分析将土壤含盐量光谱反射率划分为4类，分别对4 类光谱反射率求数学平均，得到4 种土壤含盐量的光谱曲线，土壤含盐量的光谱特征整体较为相似。在波段为350～1 340 nm 之间，土壤含盐量为4.20 和2.51 g/kg 的光谱反射率值高于1.56 和3.17g/kg 的光谱反射率值；在1 340 nm 之后，这4种土壤含盐量光谱反射率值则显示相反的变化规律，土壤含盐量为3.17 g/kg 的反射率值较高。总体上看，350～2 100 nm 之间，土壤含盐量光谱反射率值随着波长的增加而增加，2 100 nm之后，光谱特征逐渐减弱。

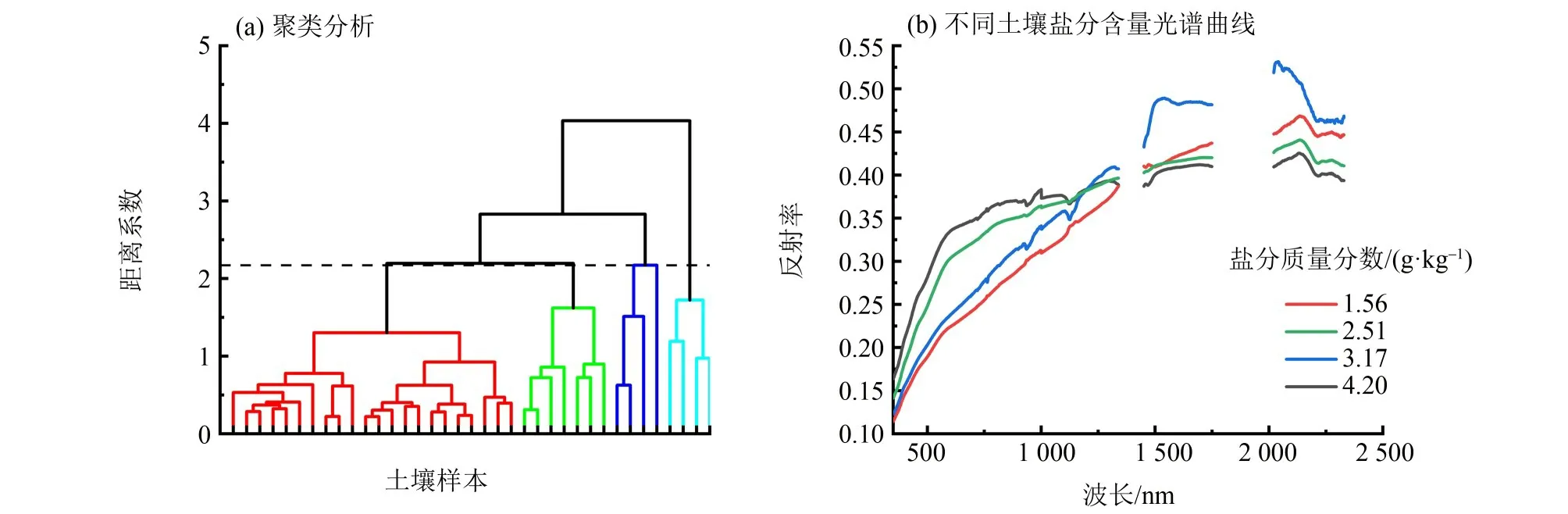
图2 土壤含盐量光谱曲线聚类分析和不同土壤含盐量平均光谱曲线特征Fig.2 Cluster analysis of soil salt content spectral curves and characteristics of different soil salt content average spectral curves

2.2 分数阶微分对相关系数的影响

将原始光谱反射率的分数阶微分及其4种不同变换形式下的分数阶微分与土壤含盐量在0.01 极显著水平下进行相关关系分析。如表2所示，通过显著性检验较多的特征波段数是1/R为691个波段，最少的是1/lgR，为300 个波段。原始光谱反射率通过显著性检验的特征波段主要集中在1阶～2阶，1/R 的0 阶微分是唯一通过显著性检验的阶数，且通过0.4 阶和0.6 阶的特征波段比其他光谱反射率分数阶微分的特征波段数多，分别为145 和150。随着阶数的增加，通过显著性检验的特征波段呈现先增加后减少的趋势，R 的1.2 阶的特征波段最多为142， R 的0.6 阶的特征波段最多为95，lgR的0.6 阶的特征波段最多为115，1/lgR 的0.8 阶特征波段最多为56。

由图3可知，通过显著性检验的特征波段集中的范围，原始光谱反射率R的特征波段分布在638～653，1 166～1 181，1 234～1 237，1 669～1 749 和2 021～2 329 nm。 R 与lg R 的特征波段集中范围较为相似，1/R 与1/lg R 的特征波段集中范围较为相似，且4 中数学变换的特征波段主要集中在600～1 000 nm 和2 020～2 330 nm，这与R 分布的特征波段数量有很大的不同。R 的相关性极大值绝对值是2 阶为0.53， R 的相关性极大值绝对值是0.8阶为0.67，1/R 的相关性极大值绝对值是0.6 阶为0.69，lgR 的相关性极大值绝对值是0.8阶为0.67，1/lgR的相关性极大值绝对值是0.6阶为0.64。

2.3 土壤含盐量分数阶微分的光谱建模与验证

分别利用通过显著性检验的R、 R、lg R、1/R、1/lg R 特征波段与土壤含盐量进行偏最小二乘回归，建立不同光谱变化下分数阶微分的土壤含盐量估算模型。由表2 可知，从总体上看1/lg R 的0.2 阶和1/R 的1.8 阶的建模效果较好，分别为0.78 和0.75，RMSEC分别为1.56和1.48。从原始光谱和4种光谱变换下的验证集可知，R 的1.8阶的估算模型较好为0.47，而RMSEV为1.65的1.2 阶的估算模型较好为0.57，RMSEV为1.48；1/R 的1 阶和2阶的估算模型精度较好，分别为0.52、0.53，RM⁃SEV分别为1.35、1.34；lg R 的0.8 阶和1 阶的估算模型精度较好，分别为0.52、0.52，RMSEV分别为1.43、1.33；1/lg R 的0.2 阶和0.4 阶的估算模型精度较 好，分 别 为0.63、0.62，RMSEV分 别 为1.44、1.42。由图4 可知，1/lgR 的分数阶微分拟合曲线较为集中，从来看，最小值为0.47，其他主要在0.50～0.54，R的分数阶微分拟合曲线较为杂乱。

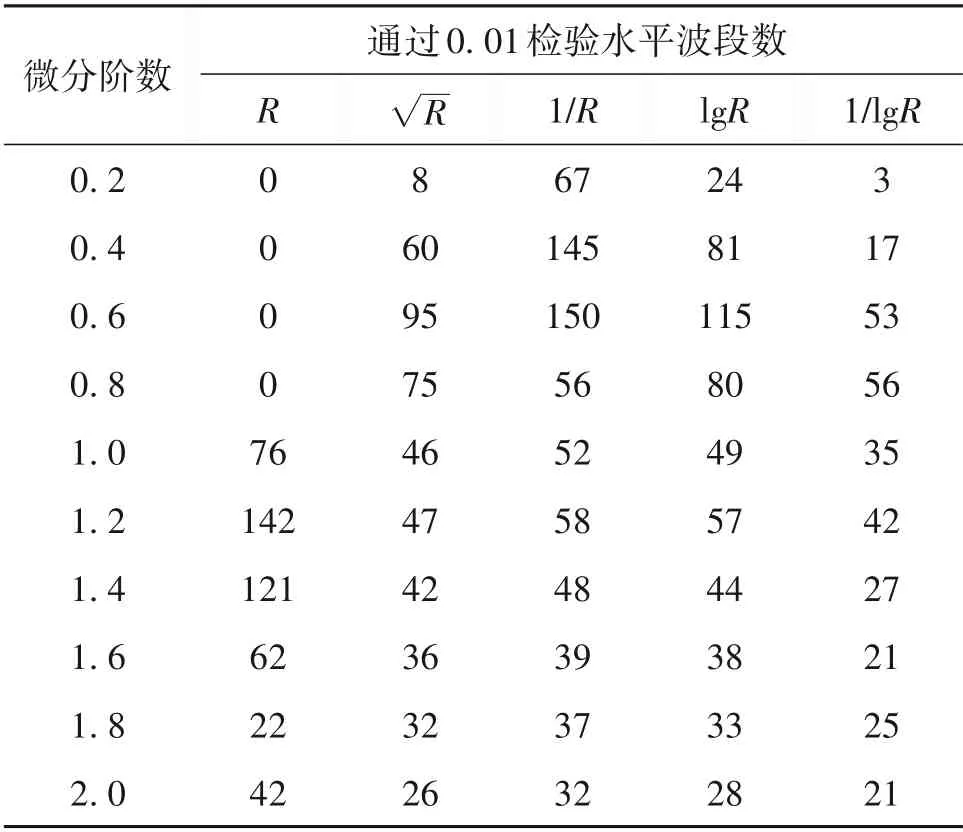
表1 分数阶微分通过显著性检验的波段数Table 1 Band numbers through significant test of each fractional-order differential

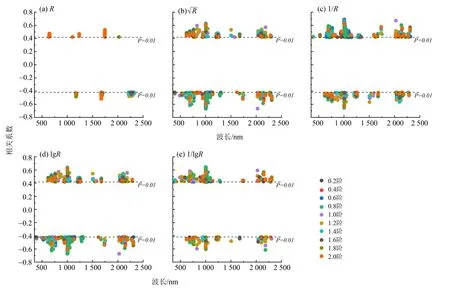
图3 土壤含盐量与不同光谱变换反射率分数阶微分的相关系数Fig.3 Correlation coefficients between soil salt content and various order differentials of reflectivity under different spectral transformations

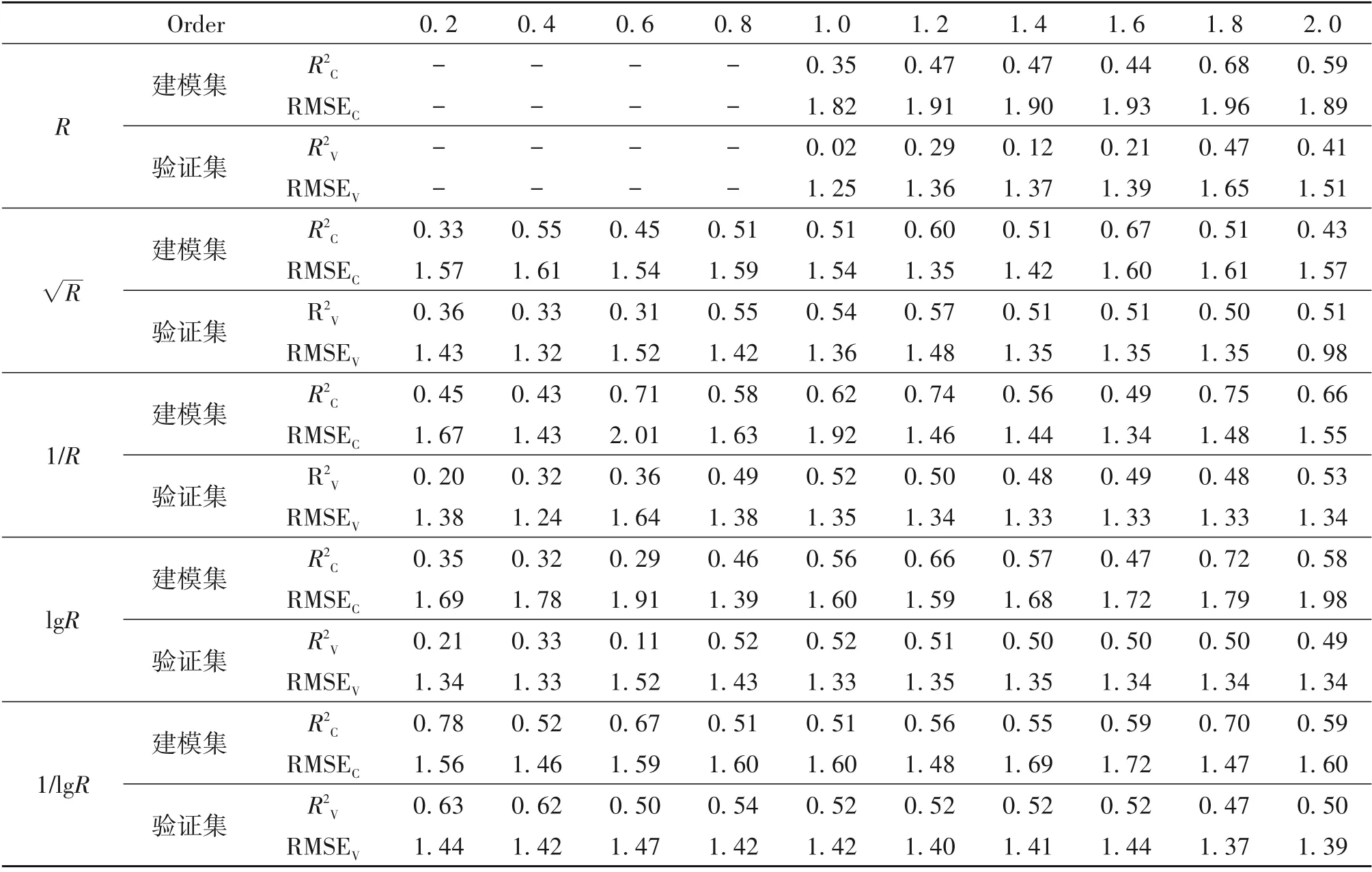
表2 土壤含盐量分数阶微分光谱建模与验证Table 2 Modeling and verification of fractional differential spectra of soil salinity

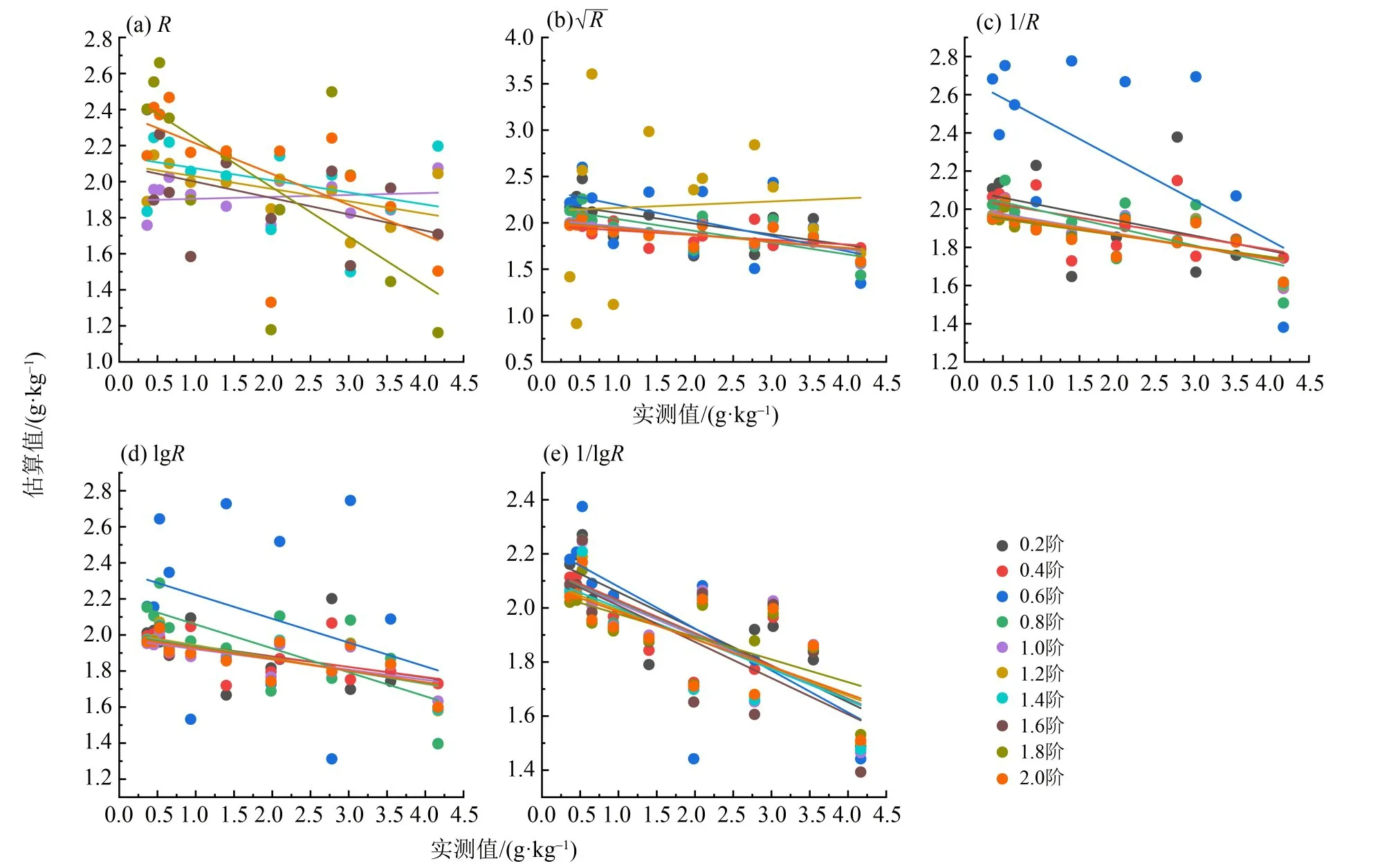
图4 基于不同分数阶微分光谱变换的土壤含盐量偏最小二乘回归模型验证Fig.4 Verification of soil salinity partial least squares regression model based on different fractional differential spectral transformation

3 讨 论

适当的光谱增强变换有利于土壤盐分信息的高光谱识别和提取，采用4 种数学光谱变换的分数阶微分进行预处理，有助于通过显著性检验优选最优光谱变换的分数阶微分特征波段。本文利用分数阶微分在阶数上，能够突破整数的限制，范围更加广泛的优势预处理数据，发现分数阶微分预处理方法可以有效地不同程度的提高数学光谱变换的相关性值。从光谱变换微分值与含盐量的相关关系数最大值，均出现在分数阶，这与文献［11，18］的研究结果基本一致。从建模集和验证集精度和误差来看，分数阶的建模效果优于整数阶，这与亚森江·喀哈尔等［13］的研究结果基本一致。分数阶微分为高光谱数据定量估算土壤盐分含量提供新的角度，说明该方法在利用高光谱数据估算研究区土壤盐分含量是可行的。研究区属于干旱区绿洲，因此，光谱变换的分数阶微分在不同地区的最佳参数并找出普适性高光谱参数，值得进一步研究。

4 结 论

1）不同的光谱数学变换的分数阶微分可以增加通过显著性检验的波段数，通过显著性检验较多的特征波段是1/R为691个波段，比通过R多226个波段；突显某些波段的光谱反射率与土壤含盐量的相关性，扩大特征波段的选择空间， R、lg R、1/R、1/lgR 通过显著性检验的特征波段主要集中在600～1 000 nm和2 020～2 330 nm。

2）随着分数阶微分的增加，通过显著性检验的特征波段呈现先增加后减少的趋势，1/R、 R、lgR均在0.6 阶通过的特征波段数最多，分别为150、95、115，R 的1.2 阶的特征波段最多为142，1/lgR 的0.8阶特征波段最多为56，均在分数阶微分达到最多。

3）在原始光谱R、均方根 R、对数lgR、倒数1/R、对数倒数1/lgR 的各分数阶微分利用偏最小二乘回归建模中，从总体上看1/lgR的建模效果优于其他4 种建模，且1/lgR 在0.2 的建模精度和验证精度较高，=0.78，RMSEC=1.56=0.63，RMSEV=1.44。通过光谱变换进行分数阶微分预处理优选特征波段，以提高土壤电导率的估算精度，为土壤盐分含量相关研究提供一种新的思路和方法。