基于特征贡献率的机械故障分类方法*
2020-08-06马波,赵祎
马 波, 赵 祎
(1.北京化工大学高端机械装备健康监控及自愈化北京市重点实验室 北京, 100029) (2.北京化工大学发动机健康监控及网络化教育部重点实验室 北京, 100029)
引 言
往复压缩机、航空发动机、大型风电装备等重大装备由于结构复杂、激励源多及工作环境恶劣,故障率通常较高。建立可靠的故障诊断系统是保证这些装备安全运行的必需举措[1]。人工神经网络(artificial neural network, 简称ANN)作为智能诊断技术的一种,已在复杂机械的故障诊断中取得了良好的应用效果[2-3]。在工程实际中,由于没有大量故障样本用于训练神经网络,限制了ANN在机械故障诊断中的进一步发展与应用。支持向量机(support vector machine,简称SVM)凭借其在处理小样本问题上的优越性,在机械故障诊断领域取得了广泛应用[4-5]。然而SVM的诊断准确率受核函数影响较大,在没有对核函数进行复杂的优化建模条件下,其识别率无法达到最优。文献[6]将Relief算法与K邻近分类器相结合,实现了复杂旋转机械的故障智能诊断且诊断效果较SVM有所提升。在设备运行状态发生变化的过程中,某些激励信号产生的变化在叠加后的响应信号中体现不明显,由于该方法只针对设备响应信号进行分析,其诊断精度难以进一步提升。文献[7]提出了一种基于GMM的故障诊断方法,该方法对设备各激励源所激发的激励信号进行深入分析,将各类故障数据的GMM作为分类指标,在给定观测数据的条件下,通过比较各故障模型的后验概率进行故障诊断,并取得了较好的诊断效果。然而其在构建机械振动信号高维特征的GMM时,分布分量的数目需人工设定,若选取不当,则所构建的模型难以符合信号实际的分布特点,使得某些种类故障数据的统计分布模型间差异不明显。因此,该方法的泛化性能较差。
DPMM是非参数贝叶斯统计的基石,能够自学习出数据所服从的统计分布,无需人工设定分布分量数目,且狄利克雷过程(Dirichlet process,简称DP)能够为模型参数的分布提供先验[8]。凭借这些优点,DPMM已在文本聚类、图像分割等方面的数据分布自学习上取得了良好的应用效果[9-10]。因此,若能将DPMM应用到机械振动信号的统计分布自学习中,则对于提高复杂机械故障诊断准确率具有重要意义。为提高建模后诊断方法的泛化性能,需选出一种具有高区分度的分类指标。BIC为突显复杂机械各类故障数据间的差异提供了新途径[11]。BIC是一种基于统计分布模型的特征评估算法,其算法原理是根据观测数据中各特征参数与统计分布模型中分布分量的相似度进行评估得到贡献率(即权值)。基于BIC的方法通过确定贡献率最高的主导变量,实现了多种工业过程中故障的准确诊断[12]。依据机械振动信号的特征参数对不同故障的敏感度存在差异这一特性,在准确构建出振动信号高维特征统计分布模型的基础上,计算特征贡献率并将其作为分类指标,能够突显各类故障数据间的差异。由于机械响应信号统计分布模型中的分布分量能够表征各激励信号所服从的分布,响应信号的特征贡献率则为特征参数在各激励信号分布中贡献率的综合表示,因此,该分类指标能够准确反应故障发生时各激励信号产生的细微变化。
基于上述说明,提出一种DPMM与BIC相结合的分析方法。采用DDPM方法自学习机械振动信号高维特征的统计分布模型,并依据BIC理论计算特征贡献率,通过分析观测数据与各类故障数据特征贡献率间的距离(即差异度),实现故障分类。试验结果证明了该方法的可行性与有效性。
1 理论基础
1.1 狄利克雷过程混合模型
若某层次模型的参数服从DP先验分布,则该模型被称为DPMM。DP定义为关于一组分布或者随机测度的分布,可以看作是推广的无限维狄利克雷分布。DP的截棍构造[13]表示如下
其中:vk与ηk为两个独立的随机变量;vk~Beta(1,α),k={1,2,…};ηk~G0,k={1,2,…};α与G0分别为DP的尺度参数与基础分布;δηk表示中心为ηk的Delta函数。
用截棍法构建DP,可得到DPMM的截棍构造表示
其中:Zn为指示变量且服从多项式分布;φ(v)为混合模型的权重向量;X为观测数据集;η为混合模型的参数集,包括均值向量μ与协方差矩阵Mcov。
向量φ(v)用于产生指示变量Zn,进而将Xn分配到指定的分布分量上,实现样本聚类。
1.2 模型的训练
采用平均场变分推断方法近似隐变量W={v,η,Z}在DPMM中的后验分布p(W|X,θ),其中θ={α,λ}为模型的超参。构造一个由变分参数ε索引的分布族qε(W),模型训练的目标是最小化qε(W)与p(W|X,θ)间的KL散度
(7)
利用KL散度为非负数的特点,对式(7)进行变换,得到
logp(X|α,λ)≥L
(8)
其中:
(9)
根据式(8),模型的训练目标转变为最大化边缘似然对数的下界L。
通过采用截断的截棍过程表示和因式分解假设,用于平均场变分推断的变分分布族可表示为
(10)
其中:qγt(vt)为beta分布;qτt(ηt)为拥有自然参数τt的指数分布族;qφi(zn)为多项分布;截断级T为能够被自由设置的变分参数。
根据式(10),自由变分参数可表示为
ε={γ1,γ2,…,γT-1,τ1,τ2,…,τT,φ1,φ2,…,φN}
(11)
通过迭代更新ε使得L逐步增大,最终得到一个局部最大值并获得模型参数。
1.3 贝叶斯推断贡献
BIC是一种基于统计分布模型的特征评估算法,可用来表征观测数据中各特征参数对统计分布模型的贡献率。其算法可描述如下:对于任意一个训练样本Y,其统计分布模型记为C={Cm|m=1,2,…,K},首先计算Y中各特征参数的平均值并得到一组特征向量y,然后分别计算y在各分布分量Cm中的后验概率
(12)
其中:K为统计分布模型中分布分量的个数;ηm为第m个分布分量的参数;φm为第m个分布分量的权重。
y中各特征参数与Cm的相似度可通过被分解的正则化马氏距离矩阵表示
(13)

若Mdm在某特征维度上数值越大,则表明该特征对Cm的贡献率越高。
y中各特征参数对统计分布模型C的贡献率可表示为
(14)
在实际应用中,R能够被归一化。
2 故障分类方法
复杂机械响应点的响应函数[14]为
(15)
其中:Y(t)为t时刻响应点的响应信号;Fm′(t)为t时刻第m′个激励源的激励力函数;Hm′(t)为t时刻第m′个激励源到响应点的激励信号传递路径的传递函数;K′为激励源数量。
由于设备激励信号变化过程服从某个未知分布,根据式(15),响应点响应信号的分布即为各未知分布的线性叠加。若设备发生故障,某些激励力响应函数会发生改变,使得响应点响应信号的分布产生相应变化。DPMM能够自学习出数据所服从的统计分布,因此可准确表征不同故障振动信号的分布特点。复杂机械都是多自由度非线性系统,即高维非线性系统。高维系统所有可能状态的集合称为相空间[15],若设备运行状态发生改变,其相空间必然发生变化。因此,构建设备振动信号的特征相空间矩阵,并将其作为DPMM的训练样本,能够提高模型的稳定性,使其更准确地表征设备在发生不同故障时的运行状态。
故障分类方法的流程如图1所示,主要包括构造特征相空间矩阵、训练模型、计算特征贡献率及故障分类4个部分。
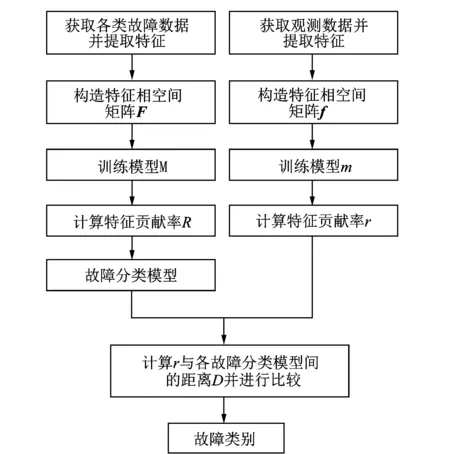
图1 故障分类方法流程图Fig.1 Flow diagram of fault classification method
2.1 特征相空间矩阵的构造
故障诊断实际上是一个模式识别问题,而特征的提取和选择是模式识别的关键。为了尽可能全面地反映设备运行状态,笔者从时域、时频域角度选取了机械故障诊断的常用特征,并依据往复压缩机运动特点增加了角度域特征。在运用类内类间距离准则对特征进行优化后,最终得到34个最优特征,如表1所示。获取N组不同类型故障的训练样本Xi,i∈[1,N],提取特征并构造特征相空间矩阵Fi,i∈[1,N]
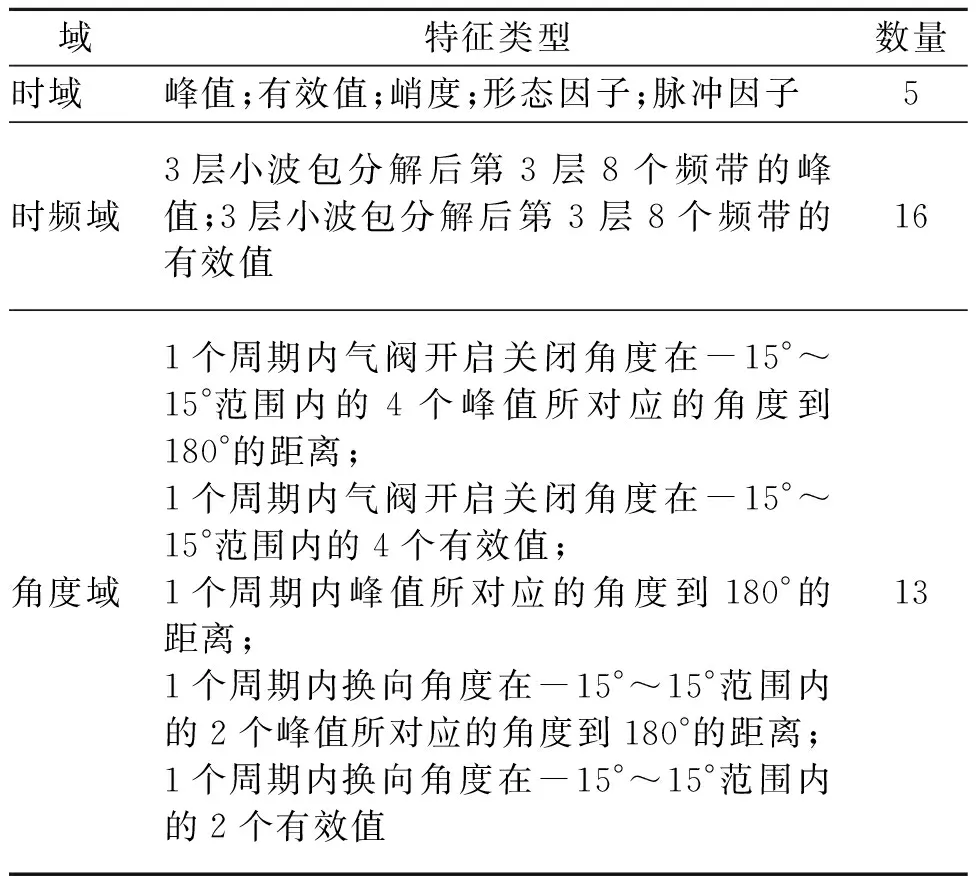
表1 特征类型说明
(16)
其中:b为每个训练样本中包含的数据组数;Fi(a)为第a组数据的特征矩阵;fe×g为第e个测点信号的第g个特征;q为监测点数量;p为特征数量。
2.2 模型训练
将Fi作为DPMM的训练样本,其与式(6)中观测数据集X相对应。输入样本后,采用平均场变分推断方法近似隐变量Wi={vi,ηi,Zi}在模型中的后验分布p(Wi|Fi,θi)。在求得变分分布族后,通过迭代变分参数εi,使logp(Fi|θi)的下界L达到一个局部最大值,进而求得各分布分量的权重与参数。
利用DPMM方法自学习出的机械不同故障振动信号的统计分布模型Mi,i∈[1,N]可表示为
其中:ηi和φ(vi)分别表示该分布模型的参数集与权重向量。
2.3 特征贡献率的计算
对于给定的Fi,首先计算其中各特征参数的平均值并得到一组特征向量yi,然后分别计算yi在Mi各分布分量中的后验概率
(21)
其中:K为Mi中分布分量的个数。
yi中各特征参数与Ci,m的相似度可表示为
(22)
根据式(14),计算各类故障数据的特征贡献率并将其作为分类模型
(23)
2.4 故障分类
计算观测数据的特征贡献率r,并将其与各分类模型Ri(i∈[1,N])进行比较,其间的差异反映了观测数据与各类故障数据的相似程度。由于特征贡献率维度较高,难以通过直接观察判断其间的差异,因此,提出一种基于距离的差异度表示方法
(24)
其中:L为特征种类的数目。
将特征贡献率间的差异表示为一个数值,能够直观有效地进行故障分类。
3 试验验证
3.1 故障数据
所提出的方法通过将设备振动信号中各激励信号成分进行准确区分,并在此基础上计算特征贡献率进行故障分类。往复压缩机作为复杂机械装备的一种,激励源较多,其响应点的响应信号与结构相对简单的机械装备的响应信号相比包含有更多的激励信号成分,由故障引起的激励信号的细微变化在叠加后的响应信号中更难以体现。该装备故障数据较为丰富,易于获取。因此,笔者采用往复压缩机不同类型故障的振动数据验证提出方法的有效性。
以4缸往复压缩机为例说明振动信号监测传感器的测点布局,如图2所示。加速度传感器安装在十字头上方的中体测点,速度传感器安装在曲轴箱壳体上。传感器的采样频率为10 240 Hz,往复压缩机转速为300 r/min,采样长度为往复压缩机运转的2个周期。
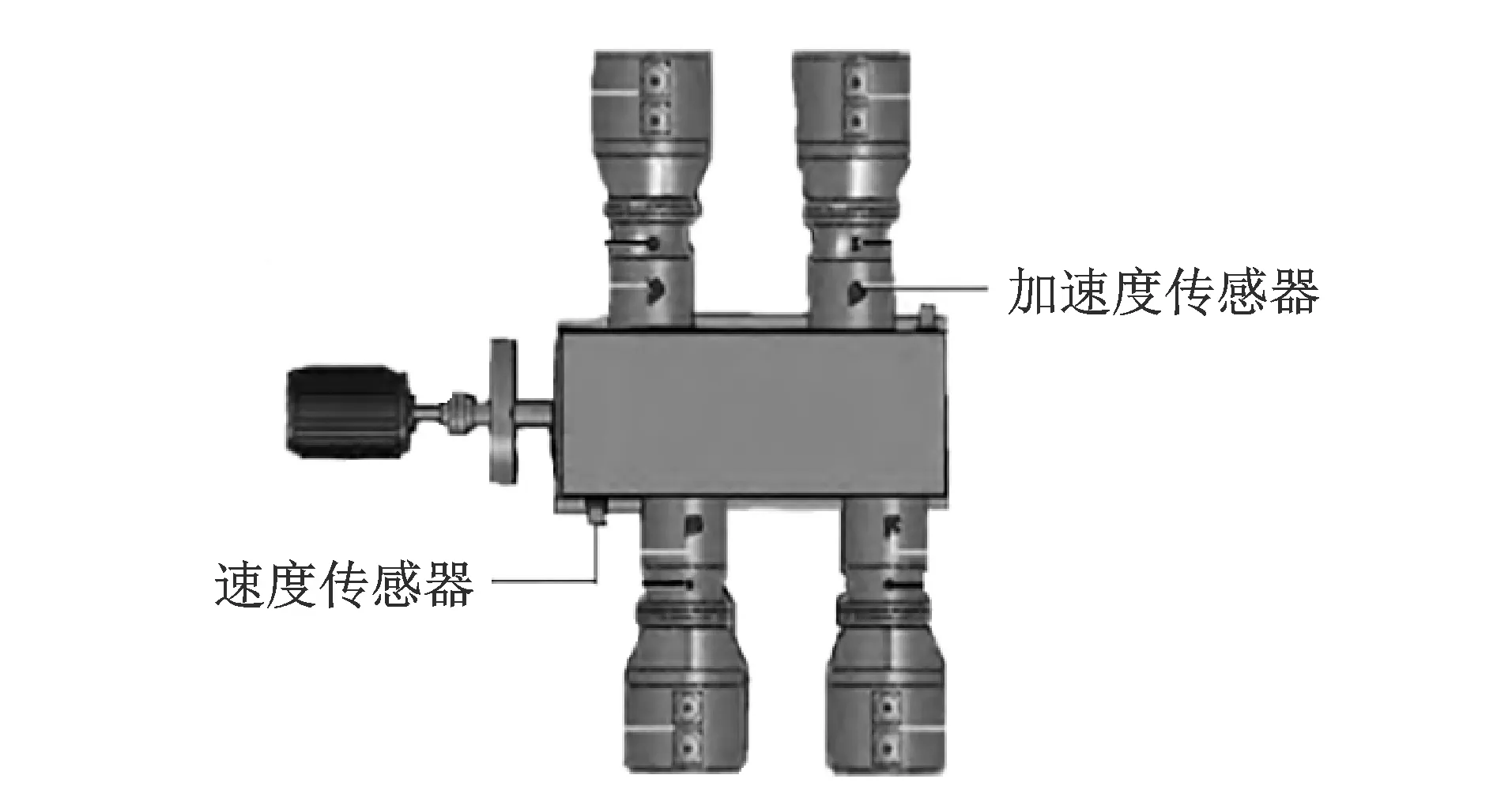
图2 传感器测点布局Fig.2 Layout of sensor measuring points
用于试验的故障案例数据均采集于石化企业的生产现场,如表2所示。由于各企业生产需求不同,同类故障案例中往复压缩机的结构形式及负荷状态不尽相同。从6种不同类型故障案例数据中各选取1组作为训练数据,其余作为测试数据。对各组数据进行样本划分,综合考虑模型训练效率和故障分

表2 故障案例数据详情
类准确率,每个样本包含的数据组数设为400,划分后的各组数据均包含丰富的样本。从6组训练数据中各随机选取1个样本用于构建分类模型,从测试数据中各随机选取1个样本用于对所提方法进行测试。为了减少随机因素的影响,试验重复进行20次。
3.2 试验结果及分析
该方法的试验结果如图3所示,可以看到,20次试验的分类准确率均为100%,充分说明提出的方法可以准确识别往复压缩机不同故障模式下的6种健康状况。为了比较,使用文献[7]方法(GMM方法)与基于Relief算法的故障诊断方法(Relief方法)诊断相同的数据。测试GMM方法时,分布分量的数目设置为3。测试Relief方法时,使用与提出方法相同的距离计算方法来表示不同特征权重间的差异。两种对比方法的试验结果也示于图3中。观察分类结果可以看出:GMM方法20次试验的分类准确率在60%~94.29%范围内, 变化幅度较大,分类精度不稳定;Relief方法的20次试验分类准确率在62.86%~74.29%范围内波动,准确率整体偏低。为了定量对比3种方法的分类精度,计算20次试验的平均分类准确率以及相应的标准差,如表3所示。可以看到,在分类精度方面,所提方法最高,其平均分类准确率为100%;Relief方法最低,其平均分类准确率仅为67.29%。在分类稳定性方面,所提方法最稳定,其分类准确率的标准差为0;GMM方法最不稳定,其分类准确率的标准差高达8.54%。当训练样本相同时,提出的方法训练模型的时耗较少,具有更高的时效性。以上结果表明,笔者所提方法的故障分类能力相比于其他两种方法均有明显优势。
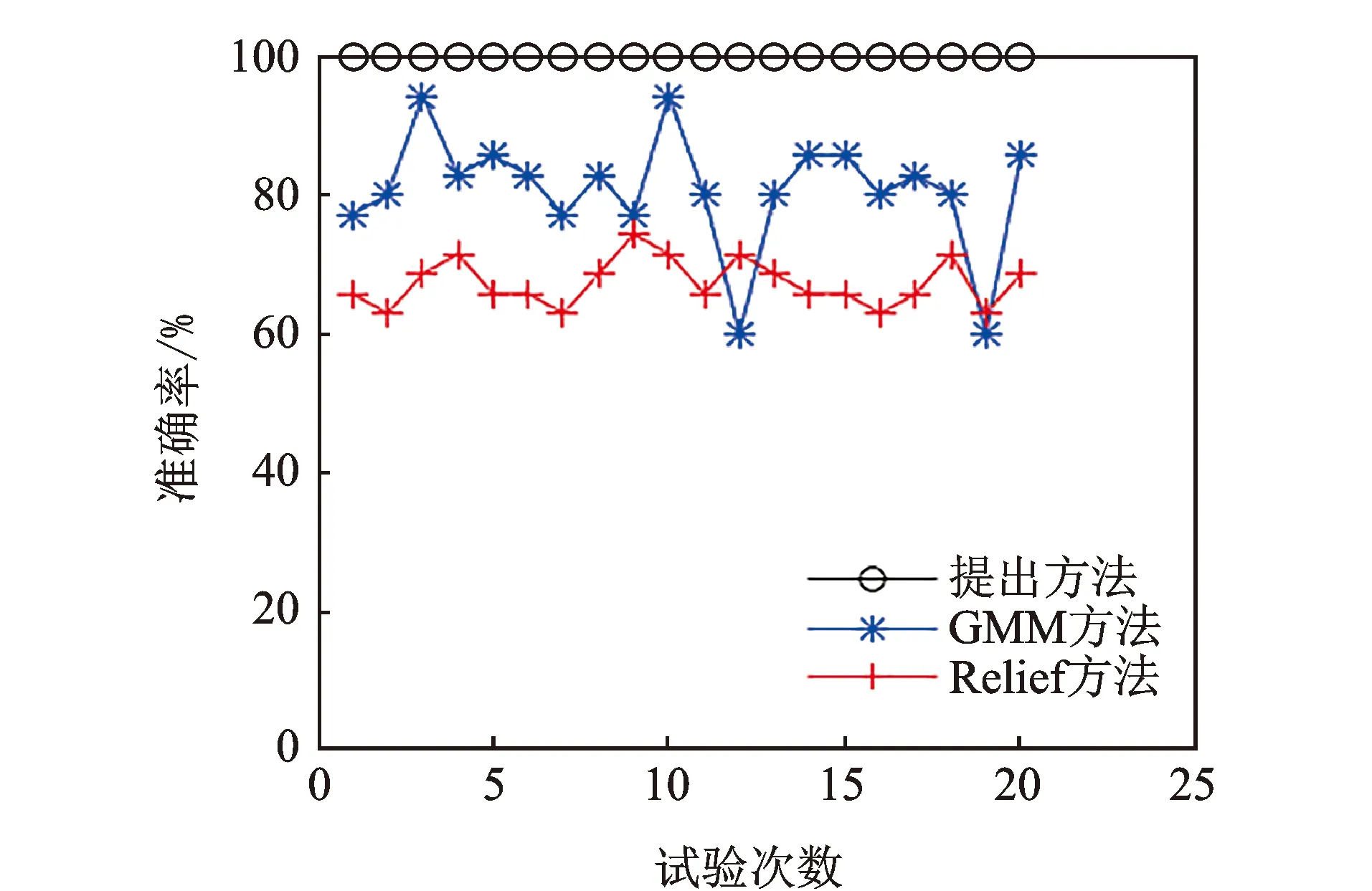
图3 20次试验中的分类准确率Fig.3 Classification accuracy of 20 tests
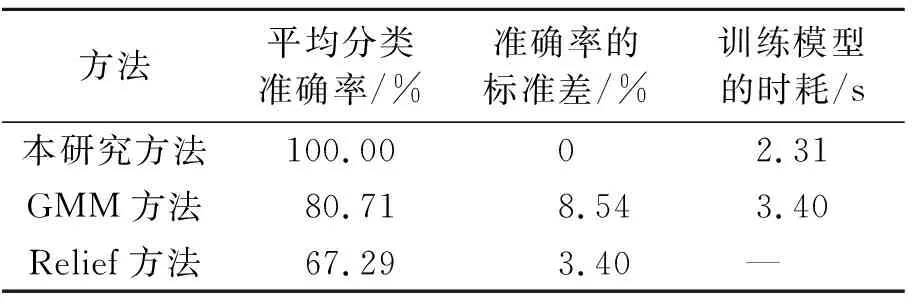
表3 3种方法的试验结果对比
通过对图3的观察,发现GMM方法的第12次与第19次试验只获得了60%的分类准确率,第3次与第10次试验却获得了94.29%的分类准确率,因而以第12次与第19次试验为代表具体分析。表4为2次试验的结果详情,可以看到,GMM方法在2次试验中都无法对撞缸、液积以及拉缸故障进行准确分类。
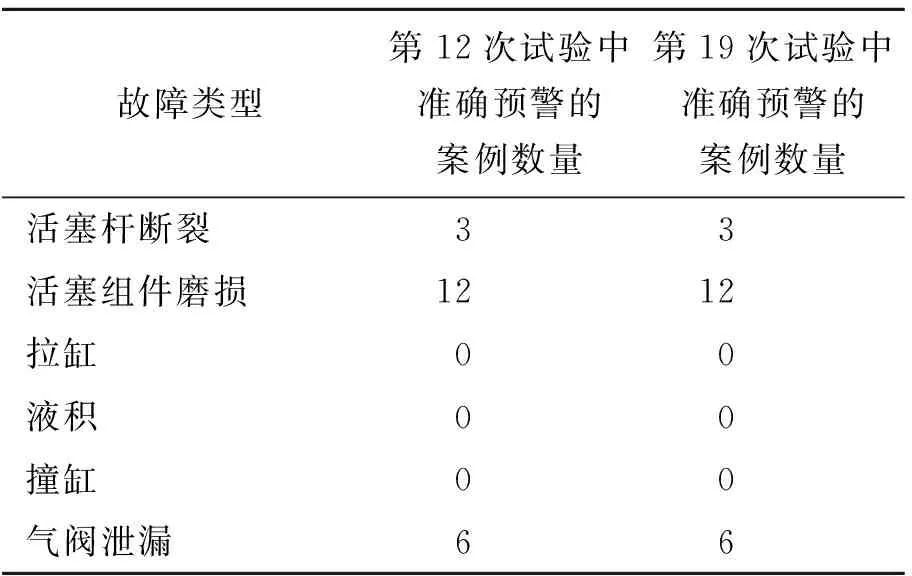
表4 试验结果详情
以撞缸故障为例,GMM方法对20组测试样本的故障分类效果如图4(a)所示。通过观察可以看出,在给定测试样本的条件下,撞缸、液积与拉缸故障模型的后验概率(无量纲)较为接近,存在误报警现象。GMM方法由于在构建往复压缩机振动信号的GMM时,分布分量的数目需人工设定,难以准确表征信号实际的分布特点,导致撞缸、液积与拉缸故障数据的统计分布模型间差异较小,无法进行准确的故障分类。
DPMM由于可以自动确定准确的分布分量数目,能够更精确地表征往复压缩机振动信号的分布特点。将GMM方法中的GMM更换为DPMM,并用相同测试样本对修改后的方法(DPMM方法)进行对比测试,试验结果如图4(b)所示。可以看出,拉缸故障模型与撞缸及液积故障模型有了明显区分,且撞缸故障模型的后验概率较GMM方法有所提升。然而撞缸与液积故障模型间差异不明显,依然存在误报警现象。所提方法将特征贡献率作为分类指标,其试验结果如图4(c)所示。可以看到,测试样本的特征贡献率与撞缸故障分类模型间的距离(无量纲)远小于其与拉缸故障分类模型间的距离,20次试验的分类准确率达到100%。该方法所构建的撞缸与液积故障的分类模型如图5所示,通过比较可以看出,机组发生不同故障后,各特征参数的贡献率(无量纲)会发生相应变化,两种分类模型间有着较明显的区别。因此,在准确表征振动信号分布特点基础上,将特征贡献率作为分类指标,能够突显不同故障数据间的差异。
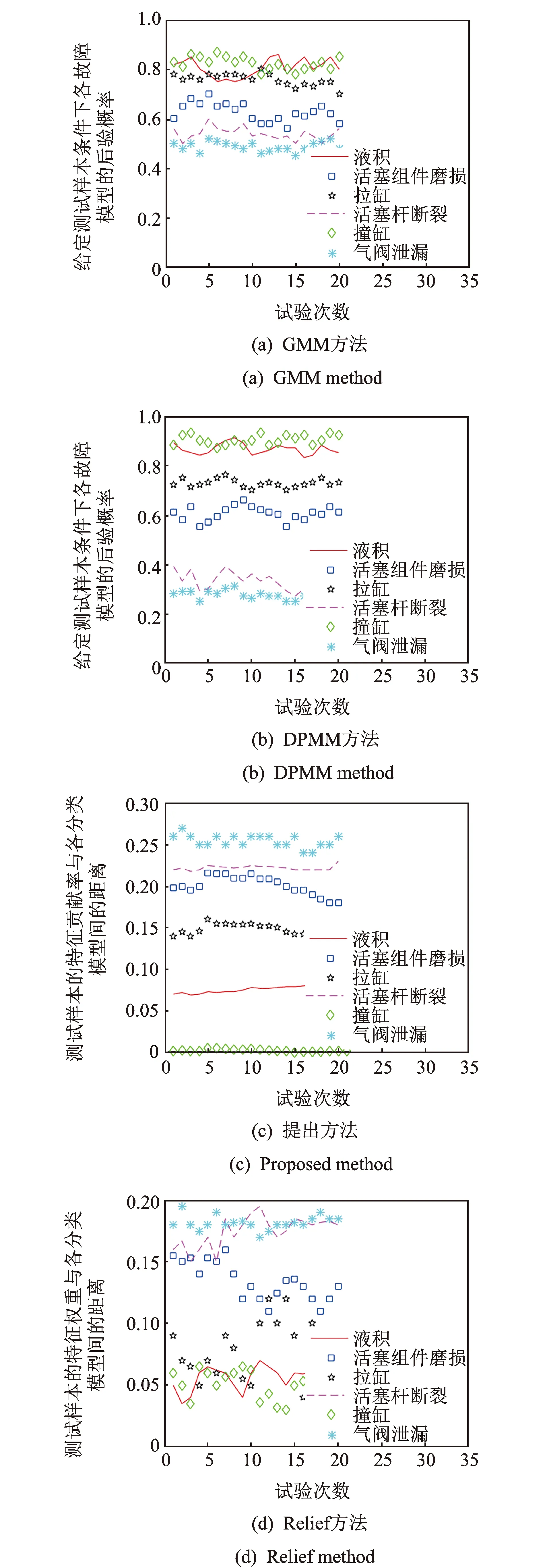
图4 撞缸故障分类效果Fig.4 Classification effect for cylinder collision fault
与提出方法的分类方式相近,Relief方法将特征权重作为分类指标,通过比较测试样本的特征权重与各类故障数据特征权重间的距离(无量纲)进行故障分类。然而该方法仅对设备响应信号进行分析,由于某些激励信号的变化在叠加后的响应信号中体现不明显,通过该方法计算得到的特征权重中难以包含有效的故障信息,且由于往复压缩机振动信号呈现非平稳性,该分类指标稳定性较差。观察图4(d)可以看出,测试样本的特征权重与各分类模型间的距离波动较大,难以进行准确的故障分类。
4 结束语
提出了一种DPMM与BIC相结合的机械故障分类方法。该方法基于机械振动信号的高维特征参数,采用DPMM方法自学习高维特征的统计分布模型,并依据BIC理论计算各特征参数在统计分布中的贡献率,通过比较观测数据与各类故障数据特征贡献率间的差异实现故障分类。试验结果表明:相对于基于Relief算法的故障分类方法,提出的方法能够深入分析设备各激励信号产生的细微变化,使分类指标中包含更丰富的故障信息;与基于GMM的故障诊断方法相比,提出的方法能够更准确地表征机械振动信号的分布特点并突显各类故障数据间的差异。该方法能够实现复杂机械常见故障的准确分类,时效性高,泛化性能强,具有重要的工程应用价值。
