含弹性约束复合阻尼板的振动机理与特性*
2020-08-06黄逸哲黄其柏
艾 振, 黄逸哲, 李 壮, 黄其柏
(1.汽车噪声振动和安全技术国家重点实验室 重庆,401120) (2.华中科技大学机械科学与工程学院 武汉,430074)
引 言
目前,基于黏弹性阻尼材料的减振结构主要有自由阻尼结构和约束阻尼结构两种,前者利用黏弹性材料的拉伸弯曲变形耗能,后者则以黏弹性材料的剪切变形耗能为主[1]。阻尼薄板结构的建模方法主要有解析法和有限元法,解析法适用于对简单结构、具有规则外形和特殊约束条件对象的建模与求解;有限元法则有效地处理各种结构形式和边界条件,并得到满足精度要求的黏弹性阻尼结构的动力学特性数值解。国内外对此进行了广泛的研究。Wang等[2]使用Kantorovich方法研究了在对边固支对边自由边界条件下局部敷设带状约束层阻尼板的动力学特性和响应问题。李恩奇等[3]采用分布参数传递函数法研究了对边简支约束层阻尼板的动力学特性。Ferreira等[4]通过Carrera统一公式,建立了含黏弹性材料核的夹芯板的分层有限元模型,并求解了频域动态问题。王慧彩等[5]构造了阻尼夹层板单元,用层合板理论建立了复合板结构的有限元模型。针对阻尼敷设的型式,目前主要有全局敷设和局部敷设,局部敷设能充分发挥单元阻尼的减振降噪作用,提高其耗能效率,更贴合工程实际应用需求。Parthasarathy等[6]研究了局部敷设自由阻尼层板的振动特性、阻尼材料的优化敷设位置。Khalfi 等[7-8]研究了局部约束黏弹性层阻尼板的瞬态响应以及不同参数下的瞬态谐波响应。在复合阻尼层研究方面,杨轩等[9]研究了缝合式复合材料夹芯板,探讨了缝合密度和缝合线角度对夹芯板动态特性的影响。漆文凯等[10]针对复合材料层合板的阻尼机理和预报方法进行了分析,采用有限元法编制了相关的模态阻尼计算程序。
区别于传统的自由阻尼层和约束阻尼层,笔者研究的含弹性约束的黏弹性复合阻尼层(composite damping layer with elastic constraints,简称ECCDL)结构由上、下黏弹性层及分界弹性层胶合而成。在振动激励作用下,其下层黏弹性层将发生剪切应变变形,上层黏弹性层产生拉伸弯曲变形,这种复合阻尼层结构综合了自由与约束阻尼层的耗能机制,并能够根据减振降噪需求进行多相材料的组合设计,具有重要的理论和实际意义。
笔者根据含弹性约束的复合阻尼层板结构的振动耗能机理,建立其控制方程、能量方程及动力学模型,并通过数值求解获取阻尼复合板结构振动耗能特性与规律,为薄板结构阻尼减振降噪提供理论基础。
1 位移场与控制方程
1.1 几何与位移
含弹性约束的复合阻尼板如图1所示,由基板b和复合阻尼层组成,其中复合阻尼层由两种不同的黏弹性材料层v1,v2及其分界层c黏贴复合而成。为便于描述,自底而上记为:b板,v1板,c板,v2板。复合阻尼层板采取以下假设:①层间完全黏着,界面位移连续;②4层具有相同的横向挠度(z向位移);③上、下板剪应力为零,c板为薄金属层,刚性大,忽略其剪切变形,故b,c,v2板采用Kirchhoff假设;④黏弹性v1层只承受横向剪切,为充分考虑剪切效应,采用Mindlin板假设。
基于假设,复合阻尼层中,黏弹性v1层剪切耗能,黏弹性v2层拉伸、弯曲耗能,其综合了约束阻尼、自由阻尼的耗能模式。描述其位移场时,采用各层板内位于中性面上的局部坐标系,均平行于图1所示的全局坐标系,图2为宽度方向的截面图,图3为板y向的变形图。

图1 含弹性约束的复合阻尼板示意图Fig.1 Composite damping plate with elastic constraints

图2 宽度向剖面示意图 图3 板y向变形图 Fig.2 Width-to-profile diagram Fig.3 y-directional deformation
建立位移场如下
(1)
(i=b,c,v2)
对于黏弹性v1层
(2)
其中:下标i代表b,c,v2,v1各层板;ui,vi为i板中性面上在x,y方向的位移;w为层合板在z方向上的位移;Ui,Vi,Wi分别为i板内点在x,y,z方向上的位移;αv,βv为黏弹性v1层变形发生在x-z,y-z平面上的截面转角[11]。
考虑到分界面完全黏着,层间无滑移,各层z向位移相同,故对于v1,v2层由分界面上x,y向位移连续条件可得黏弹性v1层上、下界面位移连续。
(3)
联立式(1)~(3),解得
(4)
(5)
剪切应变γxz,γyz为

(6)
黏弹性v2层,下界面位移连续
(7)
联立式(1)和式(7),解得
(8)
其中:hi(i=b,c,v1,v2)为各层板的厚度,此处黏弹性v1层的厚度不能为零。
经过上述方程推导转化,研究对象复合阻尼层板的位移场简化为由{ub,vb,uc,vc,w}5个场分量控制的位移场。
1.2基于应变能的能量方程
由前述假设和几何变形可知:b,c和v2板拉伸、弯曲变形时,其应变能为拉伸应变能和弯曲应变能;v1板剪切变形时,其应变能为剪切势能。设i板的应变列向量为εi,应力列向量为σi,则复合黏弹性阻尼层板的应变势能U为
(9)
对于b板
(10)
(11)
对于c板
(12)
对于v2板,结合式(8)和式(12)可得
(13)
对于v1板,应变εv1=[γxzγyz]T,应力σv1=Gv1[γxzγyz]T,结合式(6)可得
(14)
其中:Ei为弹性模量;μi为泊松比;Gv1剪切模量。
采用复常模量[12]模型描述v1和v2的黏弹性行为

(15)
其中:ζ为黏弹性材料损耗因子。
板四边约束,其x,y方向动能较小可忽略,复合阻尼层板的动能T为

(16)
其中:ρi为密度;hi为厚度。
1.3 边界、位移函数及控制方程
对四边简支板,采用假设模态法,取如下满足全部边界条件的广义位移函数[7,13]
(17)
令
则
(18)
其中:Lxb,Lyb,Lxf,Lyf为基板和阻尼层板的边长度,如图1所示;m,n为模态指标数[12];A,B,P,M,N为满足边界条件且只依赖空间x,y的位移函数的列向量表示;Γ,Θ,Λ,Ψ,Ω为只依赖时间t的新广义位移的列向量表示。
控制方程由Lagrange方程得到,定义Lagrange量为L,L=T-U,则研究的物理系统的Lagrange方程为
(19)
其中:qi=Γ,Θ,Λ,Ψ,Ω。
2 四边简支板的自由振动解与验证
结合式(9)~(19),整理转化可得广义坐标下系统的运动微分方程形式

(20)
其中:M为系统质量矩阵;K为包括耗散量的复刚度矩阵。
求解该系统的特征值方程为
(21)

2.1 算例验证
笔者研究的复合黏弹性阻尼板为4层复合板,采用退化验证。为了验证文中公式推导的正确性及解析解的正确性,计算以下两个算例。
算例1四边简支自由阻尼层合板[14-15]。令hc=0,hv2=0,为两层板,且此时v1层为自由层,拉伸弯曲耗能同前述板v2层,采用类似式(7)的位移连续关系,结合式(9)~(19)类推运动方程求解,此时广义位移只有{Γ,Θ,Ω}。如图1所示,yb=0.6 m,xb=0.8 m,hb=3.14 mm,Eb=68.5 GPa,ρb=2 700 kg/m3,μb=0.34。自由阻尼层y1=x1=0,yf=0.6 m,xf=0.8 m,hv1=4.25 mm,Ev1=4.768 MPa,ρv1=1 100 kg/m3,μv1=0.49,ζv1=0.5。表1为本研究计算结果与文献[14]解析结果、文献[15]实验结果的比较。

表1 自由阻尼板计算结果比较
算例2四边简支约束阻尼层合板[12]。令hv2=0为3层板,且v1层为约束层,如图1所示,yb=yf=0.304 8 m,xb=xf=0.348 m,hb=hc=0.762 mm,y1=x1=0,hv1=0.254 mm,ρb=2 740 kg/m3,ρv1=999 kg/m3,ρc=2 740 kg/m3,Eb=68.9 GPa,Gv1=0.869 MPa,Ec=68.9 GPa,μb=μc=0.3,μv1=0.49,ζv1=0.5。表2为本研究计算结果与文献[12]解析结果的比较。
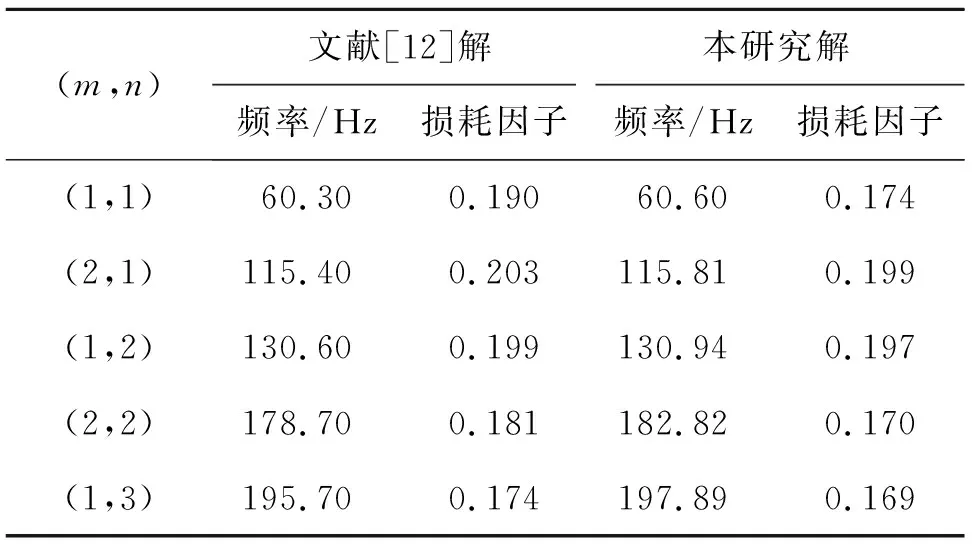
表2 约束阻尼板计算结果比较
由表1、表2中的计算结果看出,本研究求解得到的频率、损耗因子与文献中的计算结果吻合较好,验证了本研究的机理公式推导与解析计算的正确性。
2.2研究模型计算结果
研究复合阻尼层板,其参数如下。b层(铝)板:yb=0.3 m,xb=0.4 m,hb=1 mm,Eb=68.9 GPa,ρb=2 740 kg/m3,μb=0.3。复合阻尼层:y1=0.1 m,x1=0.05 m,yf=0.1 m,xf=0.3 m。v1层板:hv1=1 mm,Ev1=2.590 MPa,ρv1=999 kg/m3,μv1=0.49,ζv1=0.5。c层(钢)板:hc=0.2 mm,Ec=212 GPa,ρc=7 850 kg/m3,μc=0.31。v2层板:hv2=1 mm,Ev2=24 MPa,ρv1=1 200 kg/m3,μv2=0.45,ζv2=0.5。
计算其前5阶模态振型,如图4所示。

图4 复合阻尼层板振型图Fig.4 Mode shapes of composite damping laminates
计算3种对比算例:复合阻尼层、经典约束阻尼层和经典自由阻尼层,如图5所示。其中,控制复合板的基板厚为1 mm,板总厚3.2 mm保持不变。

图5 对比算例几何示意图Fig.5 Geometric sketch of a comparative example
对比计算结果如表3、图6所示。可以看出复合阻尼层的减振效果远大于经典自由阻尼层,效果接近经典约束阻尼。复合阻尼层综合了约束阻尼的剪切耗能和自由阻尼的拉伸弯曲耗能,其减振效果也介于两者之间。由图6可看出,模态越高,结构损耗因子减小。其第3阶损耗因子特别小,初步分析为复合阻尼层敷设位置的影响。

表3 对比算例板计算结果比较

图6 不同结构下模态损耗因子对比曲线Fig.6 Contrast curve of modal loss factor under different structures
3 不同参数下的振动耗能变化
设复合阻尼层厚度hf=hv1+hc+hv2,令基板、阻尼层厚度保持不变,研究不同hv1/hv2配比下夹层板耗能变化。夹层板的固有频率变化甚小,故只讨论模态损耗因子的变化。
如表4、图7所示,随着比值的增大,每阶的模态损耗因子均增大,即复合阻尼层中v1层比重越大,减振效果越好,这也说明了约束阻尼层的减振性能大于自由阻尼层。

图7 不同厚度比下模态损耗因子对比曲线Fig.7 Contrast curve of modal loss factor under different thickness ratios

表4 hv1/hv2不同比值下的损耗因子
如表5所示,研究复合阻尼层在不同材料参数下的损耗因子可以看出:增大上层v2层材料刚度,阻尼效果越好,即v2层刚度越大,拉伸弯曲耗能更多;对于两相黏弹性材料,下层v1层材料的变化对整体复合阻尼性能影响最大,其材料的损耗因子越大,减振性能越好。

表5 不同材料参数下的损耗因子
由于敷设位置没变,第3阶模态损耗因子依然很小。进一步分析,在将复合阻尼层的厚度及总面积保持不变的前提下,依据板前5阶模态振型形状,将夹层块变形、切分敷设在特定位置处。其敷设形状与对应阶模态振型如图8所示。

图8 不同敷设形状位置与对应阶模态振型图Fig.8 Modal shapes of different laying shapes, positions and corresponding orders
表6、表7和图9、图10列出了Ⅰ,Ⅴ型敷设下模态频率与损耗因子计算结果,敷设的形状位置如图8所示,可以看出其针对第1阶和第5阶振型敷设。结合Ⅰ型、Ⅴ型分析,Ⅴ型敷设下第1阶模态损耗因子最小,这是因为阻尼敷设位置避开了1阶振型变形密集区,1阶减振效果差,损耗因子小。Ⅴ型敷设下虽然整体减振效果不佳,但2,3,4,5阶模态下减振比重上升。由此可知,在相应模态应变能大的位置敷设阻尼有更好的减振效果,这也为局部敷设阻尼层的结构位置优化提供了一定的支持。

表6 Ⅰ型的模态频率和损耗因子

表7 Ⅴ型的模态频率和损耗因子

图9 Ⅰ型的各阶模态损耗因子曲线图Fig.9 Curves of mode loss factor of type Ⅰ

图10 Ⅴ型的各阶模态损耗因子曲线图Fig.10 Curves of mode loss factor of type Ⅴ
4 结 论
1) 建立了含弹性约束的复合阻尼板动力学模型,揭示了其剪切和弯曲复合耗能机制,分析了复合阻尼层结构参数与阻尼耗能的特性与规律。
2) 复合阻尼层的减振性能优于经典的自由阻尼层,其性能与弹性约束层的位置有关,随着弹性层位置的上移,减振性能越好。对于单一黏弹性材料,在其极限位置时复合阻尼层为约束层,减振性能达到最大。
3) 复合阻尼层中弹性层起分层作用,上层材料刚度越大,减振效果越好。对于整体复合层,下层材料对整体阻尼特性影响最大。
4) 复合板的敷设位置影响其耗能效果,基于模态振型,在相应阶模态应变能大的位置敷设复合阻尼层具有更好的减振效果。
