基于累积前景理论的组合出行交通分配模型

张雪妍，贺 锋

(中国人民解放军军事科学院 国防工程研究院，北京 100091)

0 引言

随着城市交通出行方式的多样化，出行者的出行模式从单一的交通方式出行转变为多交通方式的组合出行，如停车换乘(P&R，park and ride)出行方式。相比单一出行方式，组合出行更能刻画出行者的实际出行行为。Fernández等最早建立了固定需求下的组合出行交通分配模型[1]，在此基础上，国内外学者进行了相应的扩展研究，主要包括混合交通分配模型[2]、弹性交通分配模型[3]、随机交通均衡分配模型[4]和动态交通分配模型[5]。这些组合出行模型与单一出行方式的模型相比，不仅能够分析出行者的广义路径选择行为，同时还能研究出行者的换乘站点选择行为，为网络换乘站点的规划提供理论支持。然而，上述研究均是在确定性网络中展开的，并没有考虑交通网络的不确定性。

交通系统是典型的不确定性系统[6]，比如受天气、交通事故的影响，路网通行能力将会衰减，考虑该种不确定性，孟梦等[7]研究了降级路网下组合出行交通流分配模型与算法。但是除了交通系统的不确定性外，出行者本身还存在观测误差和非完全理性行为，因此并非所有出行者均会选择实际费用最小的路径[8]。累积前景理论是Tversky和Kahneman[9]在一系列心理学实验基础上提出的，用于描述经济行为主体面临不确定条件时的决策行为过程。研究者们通过一系列实证调研，发现累积前景理论能够很好地描述出行者在不确定环境下的路径选择行为，并将其应用于交通网络分配和路径优化等问题[10-11]。

为了定量分析随机组合网络中出行者的交通选择行为和网络均衡状态，在现有文献的基础上，引入累积前景理论，采用前景值描述出行者在不确定交通网络中的选择效用，基于随机效用理论分析了网络随机用户均衡条件，并建立了相应的变分不等式模型。该模型同时考虑了交通系统不确定性、组合出行方式、出行者观测误差和风险决策行为，可以更加精确地描述出行者的交通选择行为和网络均衡状态。

1 基本符号和理论

1.1 基本符号

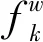
1.2 累积前景理论

累积前景理论将风险的前景和不确定性因素纳入前景理论中，用决策权重函数替换决策概率值，分别考虑损失和收益，主要包含了3个基本观点：①收益和损失是相对于参考点而言的；②面对收益人们倾向于风险规避，面对损失人们倾向于风险偏好；③人们会高估小概率事件发生的可能，而低估大概率事件发生的概率。

在累积前景理论框架下，每条可行路径对应着相应的价值函数和决策权重函数，它们的乘积为路径前景值。根据累积前景理论，出行者将路径的前景值作为路径选择依据。计算路径的前景值，需要3个基本要素，分别为路径的价值函数、参照点和决策权重函数。

(1)路径的价值函数与参照点密切相关，可以由下式表示：

(1)

式中：参数m>0，n≤1，表示出行者对价值收益和损失的敏感程度；λ≥1表示出行者对损失的规避系数；uw为参照点。

(2)采用内生的方式确定参考点[12]，即该OD对所有路径中出行时间预算的最小值：

(2)

(3)为了确保权重函数是关于到达概率的单调递增函数，采用Prelec给出决策权重函数的形式[13]：

w(p)=exp[-(-lnp)γ],0<γ<1。

(3)

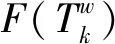
(4)

2 模型建立

2.1 路径出行时间预算

小汽车网络路段出行时间采用BPR(Bureau of Public Road)函数，即

(5)

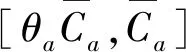
(6)

(7)

换乘时间通常由步行时间和等待时间组成。步行时间由换乘点到地铁站点的距离la,a∈E和步行速度vwalk决定，等待时间与发车间隔tf相关，假设其服从[0,tf]的均匀分布。则换乘时间的均值和方差为：

(8)

(9)

地铁运行时间相对比较平稳，几乎不受路段上流量的影响，因此可假设地铁网络的路段出行时间为一个常数定值Ta,a∈D。

假设路段出行时间相互独立，根据中心极限定理，路径的出行时间总是服从正态分布，则路径k的均值和方差为：

(10)

(11)

若给定到达概率p，则路径k的出行时间预算为：

(12)

式中：Φ-1(·)为标准正态分布反函数。

2.2 随机用户均衡条件

(13)

假设观测误差项服从独立同Gumbel分布，根据随机效用理论，选择路径k的概率为

(14)

式中：θ>0,为参数，反映出行者对路网的熟悉程度。

根据网络均衡条件，达到随机用户均衡状态时应满足如下条件：

(15)

(16)

(17)

qw≥0；

(18)

(19)

式(15)为随机用户均衡条件，式(16)为流量守恒约束，式(17～18)为流量非负约束，式(19)为路径-路段流量关系。

2.3 变分不等式模型

将随机用户均衡条件转化为等价的变分不等式模型，对模型解的存在性和等价性进行证明。

首先定义期望最小费用[16]，其表达式为：

(20)

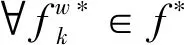
(21)

(1)等价性证明。根据变分不等式定理，变分不等式等价于如下的互补松弛条件：

(22)

(23)

(24)

(25)

对式(25)进行等价变换，即可得到：

(26)

不难看出，式(26)等价于随机用户均衡条件，从而得证变分不等式模型(21)等价于随机用户均衡条件(14～19)。

3 求解算法

如前文所述，出行者将路径的前景值作为路径选择依据，采用基于路径的相继平均算法MSA对模型进行求解，其具体步骤如下：

step4收敛检验：

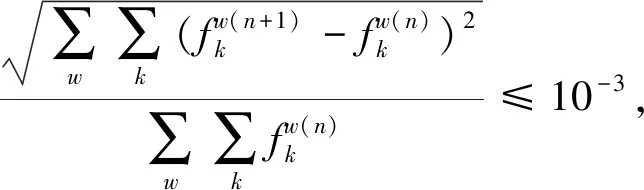
4 算例

引入“超级网络”的概念[18]，将交通网络表达为包含多个交通方式子网络的超级网络，同时在各子网络节点间添加虚拟弧段表示交通方式之间的换乘。图1展示了一个传统网络转换为超级网络的过程。

图1 超级网络Figure 1 Super network

表1 小汽车网络路段参数Table 1 Parameters for links in network of cars

表2 换乘和地铁网络路段参数Table 2 Parameters for links in network of transfer and metro

对于组合出行下的分配结果，相比路径流量，本文更加关注每个OD对中选择小汽车出行和换乘出行的流量，以及每个换乘站点的流量。下面将分析参数变化对均衡条件下出行者交通选择行为的影响。

(1)路网降级程度和到达概率。其他参数的设置情况为，路径价值函数(1)中m=n=0.88，λ=2.25，决策权重函数(3)中γ=0.74。同时对到达概率和通行能力降级系数进行参数敏感性分析。设置高中低3种到达概率，分别对应p=0.8,p=0.5,p=0.3 3种情况；设置高中低3种通行能力降级系数，分别对应θa=0.8，θa=0.7，θa=0.6，a∈R，综合下来，共9种情形。其结果如表3所示。

由表3可知，随着路网降级程度越严重，选择P&R出行方式的出行者越多，这是因为随着θa的减小，小汽车网络出行费用均值和方差都将变大。此外，出行者更加倾向于选择离终点较远的地铁站点进行换乘，这是因为出行者换乘距离越长，获得地铁出行费用稳定性的优势越大。

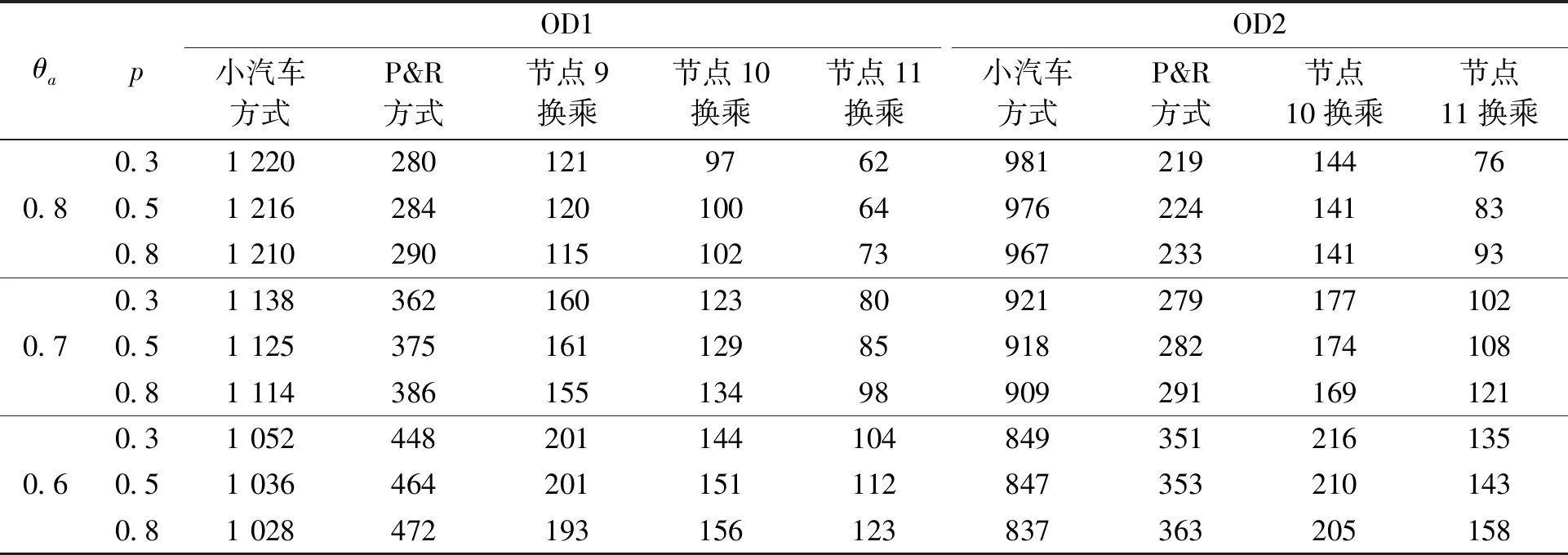
表3 不同参数下出行选择结果Table 3 Results of travel mode under different parameters pcu/h

此外，随着到达概率增加，选择P&R出行方式的出行者会增多，但并不显著。由式(2)和(12)可知，参照点会随到达概率p的取值变化而不同，对比参考文献[12]中累积前景理论下出行者的路径选择行为，出行者交通方式和换乘节点的选择行为参考点依赖效应并不显著。

(2)收益和损失的敏感性m和n。令p=0.8，θa=0.7，λ=2.25，其他参数固定不变。设置m=n，取值由低到高为0.4, 0.5, 0.6, 0.7, 0.8和0.88。由表4可知，出行者对于收益和损失的敏感性，对出行模式选择具有一定影响，且OD间距离(即OD2)越小，影响越大，其具体表现为：出行者对收益和损失越敏感，那么两种出行方式中，流量大的将越大，流量小的将越小。

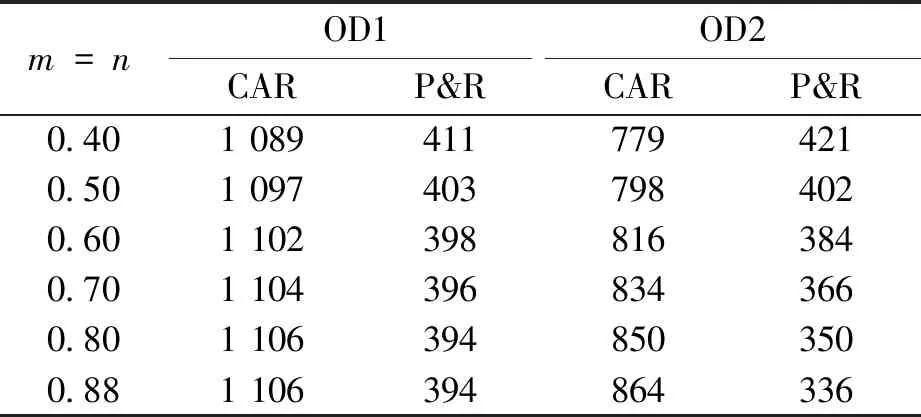
表4 不同m和n下的交通方式选择结果Table 4 Results of mode choice with variation of m and n pcu/h

(3)出行者损失规避程度λ。令p=0.8，θa=0.7，m=n=0.88，其他参数固定不变。设置λ取值由低到高为1, 1.25, 1.5, 1.75, 2和2.25。由表5可知，出行者损失规避程度对于出行模式选择影响程度较弱，但从中也能发现：出行者损失规避程度越大，两种出行方式中，流量大的将越大，流量小的将越小，这与出行者对于收益和损失的敏感性参数分析结论是一致的。

表5 不同λ下的交通方式选择结果Table 5 Results of mode choice with variation of λ pcu/h

综上所述，累积前景理论框架下出行方式的选择规律，与现有文献中路径选择规律有着一定的相似性，这是因为出行方式选择是广义路径选择的集计过程。此外，组合交通出行模型还能够辨析出行者的交通方式和换乘节点的选择行为，比单一交通出行模型具有更广泛的应用价值。

5 结论

对组合出行网络交通分配模型和算法进行了研究。为了考虑不确定环境下，组合出行网络中出行者的观测误差和风险决策行为，基于累积前景理论和随机用户均衡条件，构建了相应的变分不等式模型，对模型解的存在性和等价性进行了分析，并提出了求解算法。最后通过构建包含小汽车网络和地铁网络的超级网络作为算例，对模型的参数进行了敏感度分析。算例结果表明:模型能够有效地描述出行者的交通方式和换乘站点的选择行为，此外，路网降级系数和出行者风险态度均会影响网络的均衡分配结果。本文的研究工作为城市多模式交通规划提供了理论支持，能够应用到交通方式划分，停车换乘选址及停车场容量规划等工作中。