基于灰色理论的铁路线路方案多目标优选分析及决策模型研究

花 超

(中铁工程设计咨询集团有限公司，北京 100055)

1 概述

铁路选线是一项复杂的系统工程，需要从经济、技术、环保及社会影响等多个层面进行综合考虑[1]。在勘察设计的各个阶段，都需要对线路方案进行比选，然后得出符合要求的推荐方案[2]。推荐方案的优劣性直接影响铁路本身的施工运营条件和经济效益[3]。

早期的铁路建设项目只考虑工程投资、工程技术和运营条件等因素，对路网和沿线经济带等综合性概念缺乏足够的认识，比选方法大多为线性比选，主要依赖于决策者的主观经验[4]。近年来，铁路线路方案比选经历了从单一目标到多目标、从线性比较到综合交叉比选的过程[5]，虽然在一定程度上扩大了比选范围，但大多数比选方法的实质仍是将各项工程技术指标及社会环境指标换算成经济指标，在追求经济指标最优的同时，结合其他定性因素得出最优方案。然而，当各方案的指标差异不大，定性指标又互相影响时，方案比选就显得十分复杂和困难。因此，对于铁路线路方案的多目标优选问题，亟需一种可综合考虑人的主观需求和比选目标客观性的比选方法。

层次分析法(AHP法)能够对定性指标进行量化处理，利用加权的方式对各项指标进行权衡和比较，是解决多目标、多层次系统性问题的常用方法[6]。在铁路线路方案的比选中，各指标之间可视为不相互独立、关系不明确，其本质是一种灰色关系[7]。以下基于AHP法和灰色关联决策理论建立方案优选决策模型，综合考虑指标间的相对权值与关联性，为铁路线路方案的比选提供了一种新的思路。

2 铁路线路方案优选决策模型

2.1 灰色理论

灰色理论由邓聚龙提出[7]。灰色关联度分析法是灰色理论的重要组成部分，能够在充分利用白化信息的基础上减少分析误差。

2.2 递阶层次结构

建立铁路线路方案优选决策模型的关键在于能否科学地选定评价指标和评价层次。一般情况下，AHP法构建的评价体系包含三个层次：目标层、指标层和子指标层[8]。根据实际工程经验，铁路线路方案评价的层次结构如图1所示[9]。

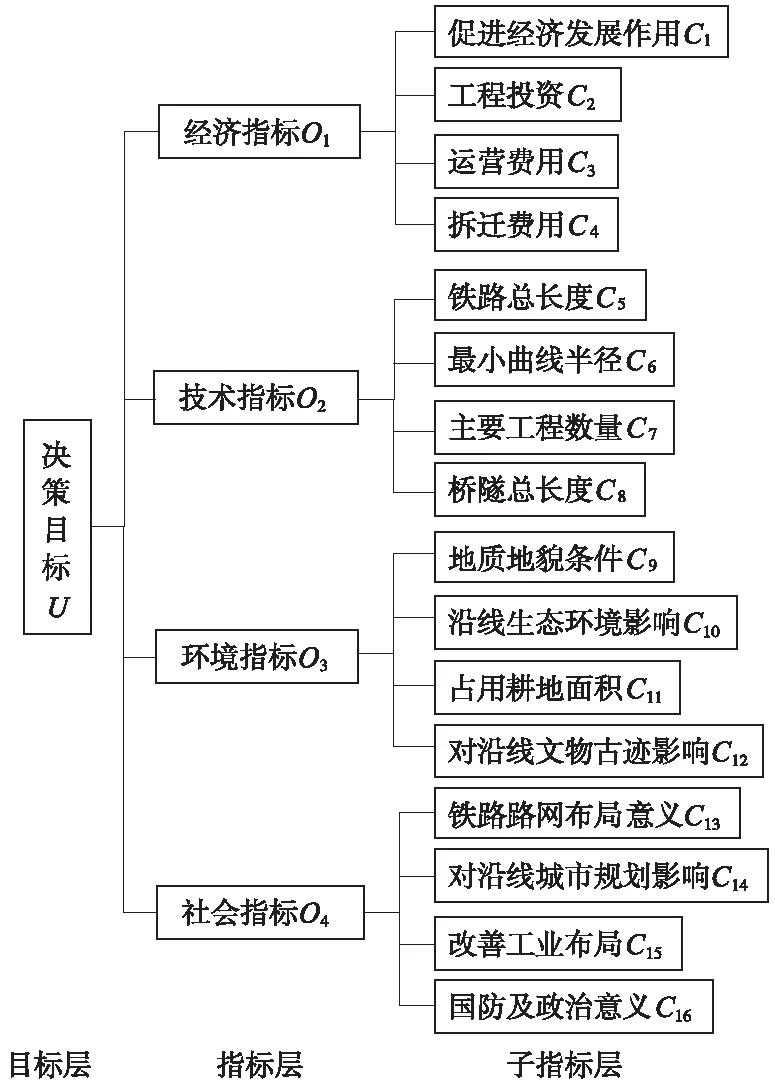
图1 铁路线路方案评价递阶层次结构

采用标度法分别对各层指标进行单排序，将层内指标两两比较，构造如表1所示的判断矩阵[10]。

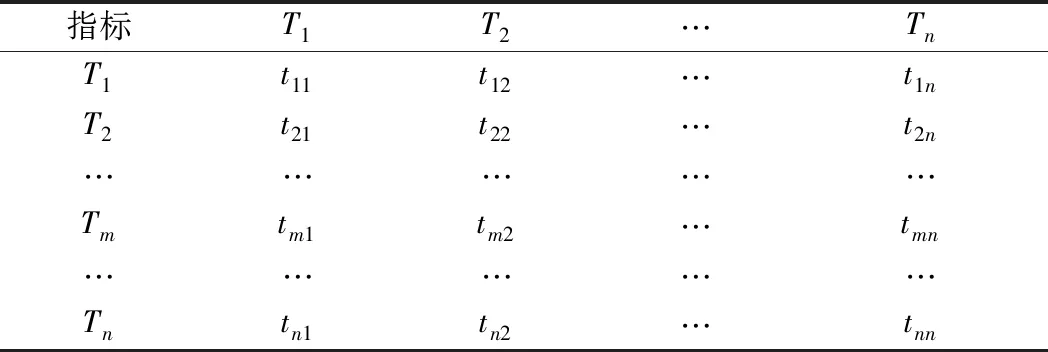
表1 判断矩阵

表1中，N为各层指标总数；Tm和Tn分别为各层第m和第n个指标；tmn为层中Tm相对Tn的重要性。

2.3 指标权值分配

确定指标权值的主要方法有行和归一法、方根法和乘幂法。其中，方根法公式简单、便于理解和编程，是目前应用最广的方法[11]。以下采用方根法，分别求解单排序和层次总排序中各层级指标的特征向量和最大特征值，有

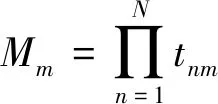
(1)

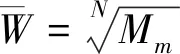
(2)

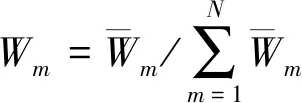
(3)

W=(W1，W2，…，WN)T

(4)

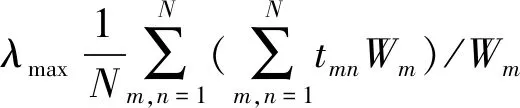
(5)

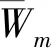
为了保证权重的合理性，需要对判断矩阵进行一致性检验，观察其是否满足一致性要求，否则应修改判断矩阵，直到满足一致性要求[12]，即

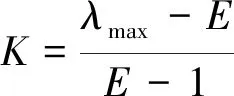
(6)

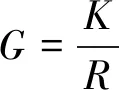
(7)

式中：K为一致性指标；G为随机一致性比率；E为判断矩阵的阶数；R为判断矩阵阶数E对应的随机一致性指标，见表2。

表2 随机一致性指标

在判断矩阵满足一致性检验的基础上，计算评价指标相对于总目标的权值

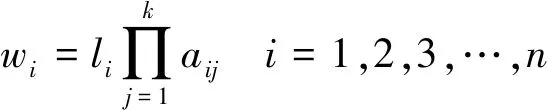
(8)

式中：li为评价指标vi在最底层单排序中计算的权值；k为子指标层vi的上一层指标个数aij；为子指标层vi的上一层指标权值，根节点ai1=1。

2.4 优选决策模型

根据灰色关联决策理论，将比选方案指标向量与相对最优方案指标向量的关联度作为评价方案优劣性的准则[13]。

假定相对最优方案为u0=(f01，f02，…，f0n)，规范化后有u0=(1，1，…，1)，比选方案ui的评价指标vi与相对最优方案u0的评价指标vj之间的灰色关联度[14]为

(9)

式中：ξ∈(0,1)ξ∈(0,1)ξ∈(0,1)ξ∈(0,1)ξ∈(0,1)ξ∈(0,1)为分辨系数，一般取0.5；i=1，2，3，…，m；j=1，2，3，…，n。

m×n个指标的铁路线路方案优选决策的灰色关联度矩阵为

(10)

n个子准则层的评价指标相对于总目标的权值向量W=(w1，w2，…，wn)T，比选方案ui与相对最优方案u0的加权关联度γi构成的关联矢量γ′为

γ′=γW=(γ1，γ2，…，γi，γn)

(11)

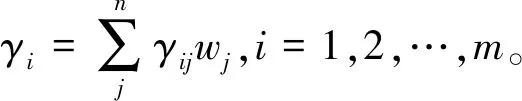
根据式(11)的物理意义，γi值越大，说明比选方案ui中的指标与相对最优方案u0中的指标越接近，故当γi=max(γ1，γ2，…，γm)时，方案ui为比选方案中的最优方案。

3 算例分析

3.1 方案数据

结合某新建铁路站位及线路方案比选进行算例分析。比较段位于某城镇内，房屋分布较为集中。确定了三个比选方案，分别为1号村庄设站方案(方案一)、2号村庄设站方案(方案二)和工业园区设站方案(方案三)，三个方案都不具备特别明显的优势，方案比选较为困难(见图2)。

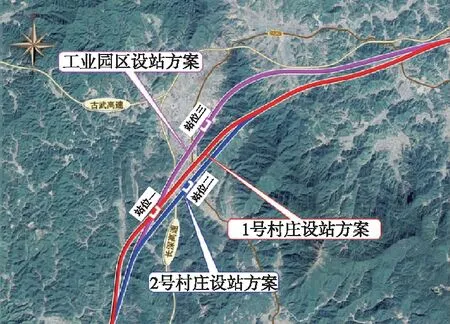
图2 比选方案平面示意

限于篇幅，仅选取部分与本段方案有关的定性和定量指标进行计算比较。对于定性指标的量化处理，采用百分制专家打分的方法。即通过咨询多位专家意见并打分，去掉最高分和最低分后取均值作为定性指标的评价参量，分数越高说明该方案在这一指标上的优势越明显[15]。三个方案的指标见表3。

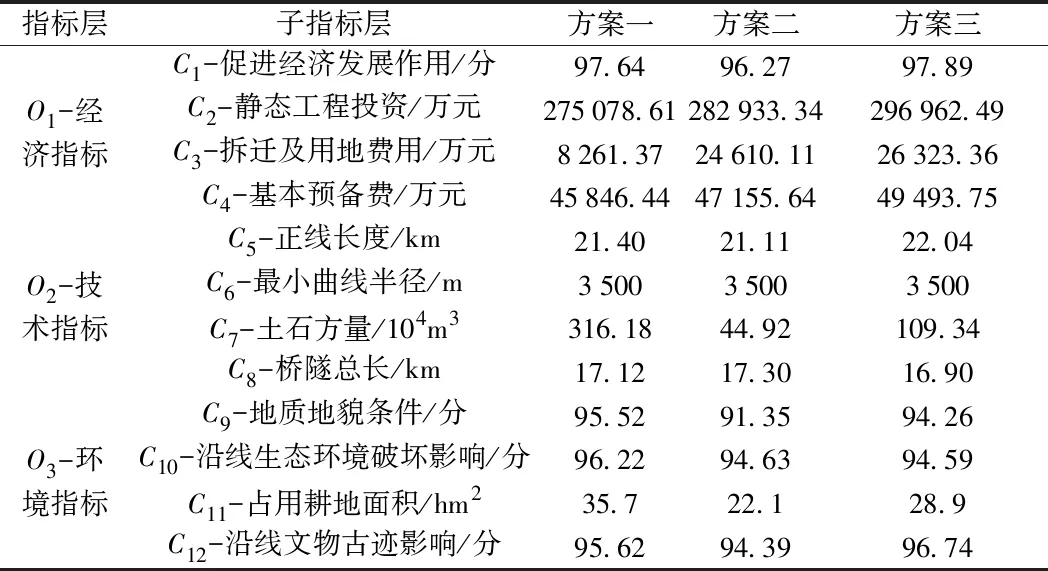
表3 评价指标

3.2 确定灰色关联度矩阵

由表3可建立方案子指标层的评价矩阵F，并选取相对最优方案u0，有

规范化处理后的评价指标矩阵为

取ξ=0.5，由式(10)确定灰色关联度矩阵，有

3.3 确定评价指标权值

根据实际工程经验和既有案例，采用标度法对各指标进行两两比较打分，本层次各元素之间的相对重要性见表4～表6。

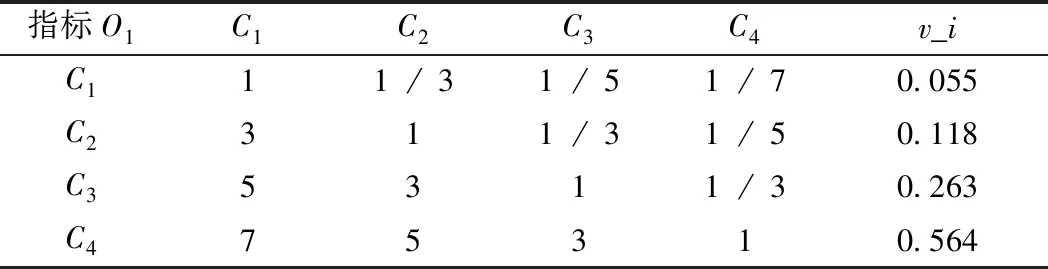
表4 O1层相对重要性矩阵

λmax=4.117

K=0.039

G=0.043<0.1

表5 O2层相对重要性矩阵

λmax=4.240

K=0.080

G=0.052<0.1

λmax=4.139

K=0.046

G=0.052<0.1

表6 O3层相对重要性矩阵

上述结果中，Ci(i=1，2，3，4)表示4项经济指标，Ci(i=5，6，7，8)表示四项技术指标，Ci(i=9，10，11，12)表示4项环境指标。设经济、技术和环境三项指标等同重要，即O1、O2和O3相对于评价总目标u的权值均为0.333。评价指标相对于总目标的权值向量为

W=(0.018 0.039 0.088 0.188 0.018 0.204

0.074 0.040 0.021 0.079 0.192)T

由式(11)可知，三个方案的加权关联度矢量为

γ′=γW=(γ1，γ2，γ3)=(0.929，0.913，0.858)

综上，方案一的评价指标与相对最优方案关联度最大，即方案一优于其他两个方案。

3 结论

采用灰色关联决策理论和层次分析法相结合的方式，提出了铁路线路方案多目标优选方法。将线路方案之间的关系视为灰色关系，首先利用层次分析法确定评价指标的权值，然后以评价指标间的加权灰色关联度作为方案优劣性的评价准则。

该方法综合了层次分析法的系统性和灰色理论的独立不确定性，在考虑了决策者主观因素的同时，也保证了评价结果的客观性。