CAPM模型的适应性研究

王向荣

摘要：CAPM模型（CapitalAssetPricingModel，资本资产定价模型）因其简便性、可理解性及可操作性，在金融学界受到了广泛应用，并对后期金融理论的发展产生了巨大影响。但随着金融体系的不断完善，一部分国内学者对该模型的有效性提出质疑。文章为检验CAPM模型对于我国股票市场的适用情况，选择了深市A股30只房地产股票进行实证分析。

关键词：CAPM模型;有效性;实证分析

一、引言

1964年，美国学者夏普夏普（WilliamSharpe）、林特尔（JohnLintner）、特里诺（JackTreynor）和莫辛（JanMossin）等人在资产组合理论、资本市场理论基础上发展出了CAPM模型。该模型得出一个非常简单的结论：如果想要获得高收益，就要投资高风险的股票。20世纪末以来，越来越多的学者开始对我国证券市场进行该模型的实证分析，有不少学者发现，我国市场不适用CAPM模型。但是随着市场机制的不断规范和完善，为了更好推动我国市场的发展，对深市进行CAPM的实证分析仍是有必要的。

二、CAPM模型介绍

（一）模型假设

1. 证券市场有效、无摩擦。

2. 投资者都是理性的。

3. 投资者具有相同预期。

4. 期望收益率和风险是影响投资决策的主要因素。

5. 可以在无风险折现率Rf的水平下无限制地借入或贷出资金。

（二）模型公式

CAPM的标准形式为：对于资产i，有

三、文献回顾

（一）国外学者对CAPM模型的研究

CAPM起源于Markowitz（1952）提出的资产组合理论，其目的是寻找有效边界，通过期望收益和方差来评价组合，投资者是理性的：想要规避风险，又想尽可能地获益。

随后，WilliamSharpe（1962）对资产组合模型进行了简化，提出了CAPM模型。

（二）国内学者对CAPM模型的研究

杨立芬（2011）选取了20只样本股票，采用FamaandMacbeth模型进行CAPM的横截面检验和采用BJS检验进行时间序列的检验，结果发现CAPM模型不适用于中国深圳的A股市场，原因是中国资本市场结构尚不健全，市场效率不高等。

张文静（2012）采用横截面检验方法和时间序列方法，对沪市进行实证分析，因为选取样本的限制、CAPM模型本身与现实情况有很大差異、我国市场相对还不够成熟等，结果显示CAPM模型在上海股市市场是无效的。

肖恒（2018）对我国证券市场中CAPM模型的适用性进行实证检验，最终得出了该理论在沪市中仅存在弱适用性的结论。原因在于：我国股票市场机制不够成熟，信息管理、披露不及时，机构投资者占比不高等，据此其提出加强法律法规建设，改善投资结构，加强市场调节机制等合理化建议。

四、实验步骤

（一）样本选取

选取深圳市场A股上市30只房地产股票的日收益率，股票的选择主要考虑以下两大因素：1.使每只股票在可用数据区间上基本保持一致，尽量减少无效数据的出现;2.对同一行业的股票进行集中选择，让CAPM实证检验结果更具说服力。采用一年期的居民存款利率2%作为无风险利率，其中一年按365天计算，这样得出的无风险利率为0.005479%。

（二）样本时期选择

2013年1月至2013年12月;2014年1月至2014年12月;2015年1月至2016年12月。

（三）数据处理过程

1. 首先将这30只股票的日收益率（对数的形式，ln（收盘价）-ln（前收盘价））整理到一个总的表格中，将表格中对数收益率计算格式有误的数据（当日收盘价与前收盘价相同）修改为0，如图1所示。

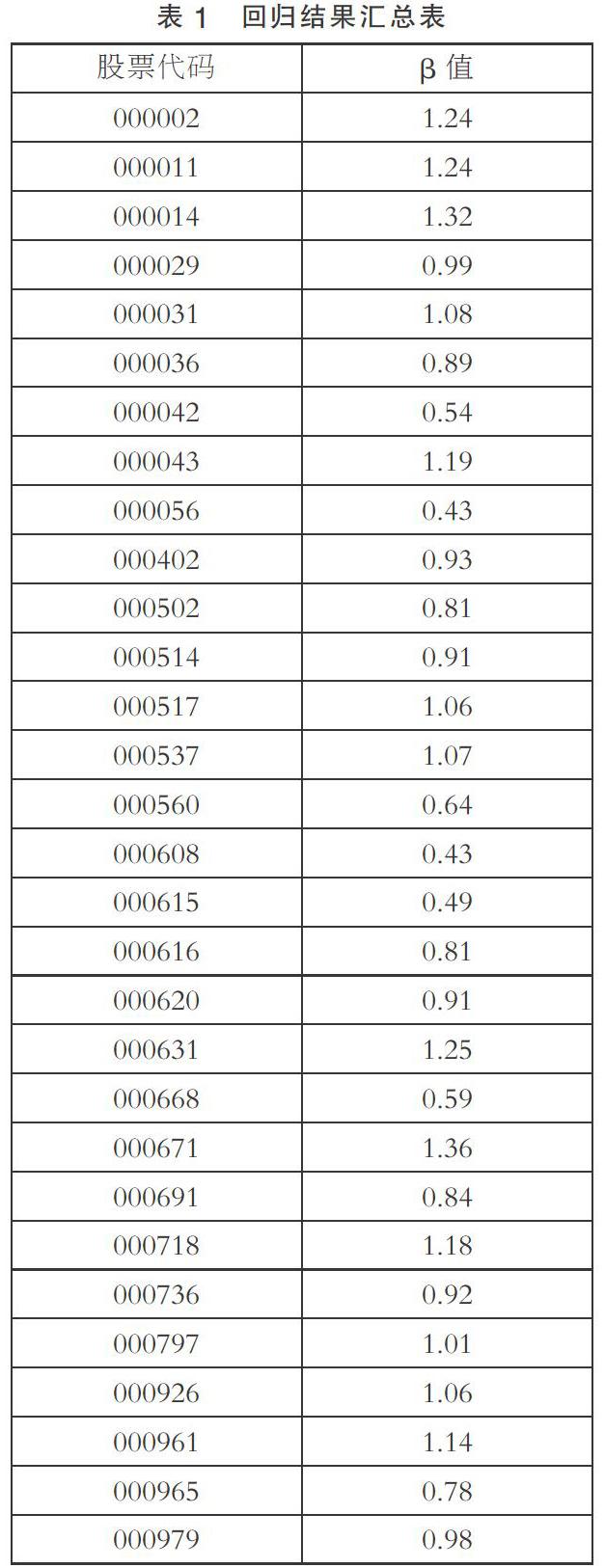
2. 运用Eviews软件，利用第一期的数据，运用OLS法进行时间序列回归，按照Rit=αit+βitRmt+εit计算单只股票βi值。回归结果如表1所示。

3. 将单只股票的βi值从小到大进行排序，并分成6个股票组合，每组含5只股票。组合结果使βi最大的5只股票分在第六组合。

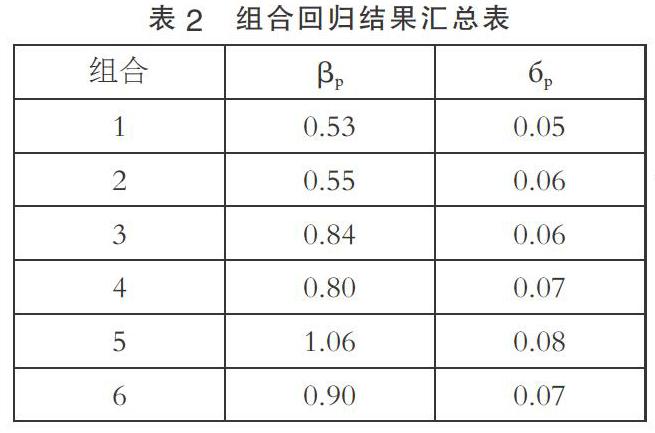
4. 在图1所示的汇总表中，根据过程3中得出的分组情况，将每一个组合的对数日收益率求平均数。

根据第二期的数据对组合的收益率与市场收益率运用OLS法进行时间序列回归，并按Rpt=αp+βpRmt+εpt计算每个组合的βp和бp。结果如表2所示。

5. 根据第三期各组合的日平均收益率和第4步计算所得的各组合βp及σp进行横截面数据回归。结果如表3所示。

Rpi是2015年1月至2015年12月的平均日收益率;βpi是组合i的β系数;λ0、λ1是待估参数;εi为残差;σpi为非系统风险。

首先采用只包括β系数的回归方程：（1）Rpi=λ0+λ1βpi+εi，结果显示：R2=0.250174，调整的R2=0.062717，说明整体性显著性差，样本拟合度弱;自变量的P值大于临界值0.05，说明自变量的显著性很差，即股票的收益与风险关系不显著;λ0为正值0.002812，与无风险收益率0.005479存在偏差，说明市场存在一定的投机行为;的值为负，说明股票系统性风险越大收益率越低，这有悖于CAPM的预期。

对于模型：（2）结果显示：Rpi=λ0+λ1βpi+λ2σpi+εi结果显示：R2=0.282481，调整的R2=-0.195865，说明方程整体性显著性很差，样本拟合度弱;但是常数项和两个自变量的P值均大于临界值0.05，说明变量的显著性很差，即股票的收益率与系统性风险和非系统性风险相关性不强。

回归结果显示，R2=0.4089，调整R2=-0.4777，各自变量的P值均大于0.05，因此方程整体及各自变量均不显著。

根据以上回归结果，深市A股地产股的收益与市场收益、系统风险、非系统风险等都没有严格的线性关系，CAPM模型不适用深市A股地产股的估值。

五、小结

根据上面的实证分析结果来看，深市房地产行业的平均收益率与系统性风险没有明显的线性关系，究其原因，可能存在以下两点：1. 样本选择的问题。本次实证分析选用了对数日收益率数据进行回归，使得检验结果或许存在误差;2. 我国深圳股票市场的不成熟。相较于外国发达资本市场，我国的资本市场尚不成熟，存在内幕交易、投资渠道不够丰富等问题，无法为投资者提供一个相对有效的投资环境，这与CAPM模型的一系列假设存在偏差，这或许也是此次实证分析与CAPM模型结论相悖的一个重要原因。

参考文献：

[1]杨朝军，邢靖.上海证券市场CAPM实证检验[J].上海交通大学学报，1998（03）.

[2]杨立芬.CAPM模型对中国资本市场的检验分析——基于中国深圳A股市场的实证检验[J].经济视角（中旬），2011（12）.

[3]李传恺.经典CAPM模型为何不适用我国[J].金融发展研究，2009（04）.

[4]张文静.CAPM模型在沪市中的有效性检验[J].时代金融，2012（36）.

[5]肖恒.基于上海股票市场的CAPM模型适用性实证分析[J].时代金融，2018（27）.

[6]王军超.CAPM模型在上海证券市场有效性分析[J].商场现代化，2012（20）.

[7]王璐，王玉静.CAPM模型及实证研究[J].劳动保障世界（理论版），2010（11）.

[8]王彦淞.CAPM模型在上海证券市场的实证分析[J].山西农经，2017（13）.

（作者单位：河北地质大学经贸学院）