基于CIR模型下的回望期权定价

贾念念 刘颖

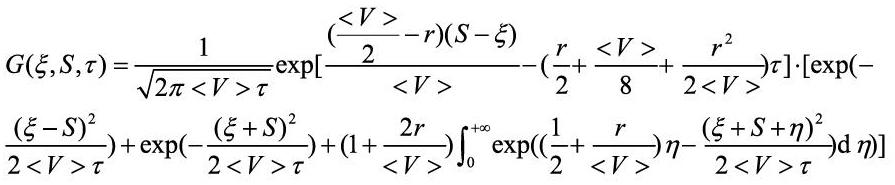
摘要：本文假设房价变化符合几何布朗运动，利用强解定理、风险中性定理等得出了基于CIR随机利率下的浮动执行价格回望看涨期权定价模型;接着根据伊藤积分的性质，利用Gisanov定理，在房价是快速均值回归假设的过程下，将期权价格C写成展开形式，通过奇异摄动方法，求出基于CIR随机房价波动率下的浮动执行价格回望看跌期权的定价模型。

关键词：回望期权  Gisanov定理  风险中性定理

一、引言

对金融产品进行合理的定价可以促进金融业务的发展，在住房反向抵押贷款的过程中，如果定价过低，房屋持有者所获得的贷款额度不够高，则参与住房反向抵押贷款的动力不足;如果定价过高，由于利率变化或房价波动率变化等因素的影响，金融机构将面临亏损，即偿还过高贷款额的情况。所以本文引入第三方金融产品来平衡两者的关系对促进新型养老业务具有重要的意义。1973年，F Black和MS Scholes首次给出了Black-Scholes期权定价模型，由此得到了Black-Scholes定价公式[1]。从美国HECM反向抵押贷款来看，該项目提供了固定利率和可调节利率两种选择。固定利率看起来更安全，但是可能使借款人面对更高的风险相对于可变利率。所以，本文引入了CIR利率，有效的克服了传统利率模型取值可能为负值的缺点，并在此基础上利用回望期权理论，得出了基于CIR随机利率和房价波动率模型下的回望期权定价公式。

二、基于CIR随机利率下的回望看涨期权价格

反向抵押贷款的贷款额度和利息和可看作标的资产的执行价格，房屋到期时价格可看作标的资产市场价格，由此可知反向抵押贷款中隐含了一个欧式看跌期权。

四、结束语

本文在传统利率模型的基础上推导出了CIR模型下的回望期权定价公式，相比欧式期权来说，回望期权的灵活性更高，对于促进养老服务业的发展，减轻社会养老压力具有重要意义。

参考文献：

[1]F.Black，M.Scholes. The Pricing of Options and Corporate Liabilities[J]. Journal of Political Economy，1973，81（3）： 637654.

[2]贾念念.基于随机利率及死亡率计算改进的寿险精算模型研究[D].哈尔滨：哈尔滨工业大学，2009： 65-80.

[3]金治明.随机分析基础及其应用[M].北京：国防工业出版社，2003： 112-204.

[4]王寿仁.概率论基础和随机过程[M].北京：科学出版社，1986： 258-282.

[5]姜礼尚.期权定价的数学模型和方法[M].北京：高等教育出版社，2008：303-309.

[6]Polyanin A.Handbook of Linear Partial Differential Equations for Engineers and Scientists. New York： Chapman & Hull / CRC，2002.

作者单位：哈尔滨工程大学数学科学学院