基于AHP—熵权法的城乡供水一体化评估模型

仇 军，卓 飞，李 岩

(1.福建水利电力职业技术学院，福建 永安 366000;2.永泰县水利局， 福建 永泰 450700；3.天津大学河流海岸工程泥沙研究所，天津 300072 )

保障饮水安全与民生息息相关，是城乡发展的基础，也是当前社会发展急需解决的关键性问题[1-3]。但受制于我国特殊的地理环境，城乡供水不足、水质偏差、管网覆盖率偏低等问题依然严峻，所以保证城乡供水安全成为当前我国急需解决的农村饮水问题，为此，我国正在开展城乡供水一体化工程，将城乡与农村互相融合一同供水。现阶段已展开有关方面的研究，时元智等[4，5]提出农村供水管理模式建议，分析云南省农村饮水安全状况，表明农村安全饮水与地区经济存在关联，沈利清等[6]探析了桐乡市存在供水问题，详细介绍了实施城乡一体化供水工程后桐乡市取得的显著成果，王浪等[7]基于山区城市供水系统的特殊性，统筹布置净水设施、输水管线等配套措施。但是相关研究多是关注效益，未将城乡供水后期管理、饮水安全、水价制定等核心问题纳入研究范围，鉴此，通过构建城乡供水一体化模型研究城乡供水影响因素，更加准确、科学评估工程整体效益，为区域性城乡供水一体化提供决策建议。

1 城乡供水一体化模型原理

1.1 评估指标划分

评估指标的划分核心是准确全面反映城乡供水过程所面临问题，评估指标需要具有全面性、可操作性、层次性以及动态性[8-10]。而城乡供水一体化涉及农村与城市，各级评估指标之间互相关联，互相制约，为了模型评估准确性和实用性，评估过程中将评估指标划分3层，各层对不同指标进行归类划分。

1.2 评估指标处理

根据评估指标特征将其分成定性和定量两类评估指标。定性指标具有模糊性，不能精确用具体数据计算表达，需采用模糊数学计算方法对其进行量化处理，考虑模型的特殊性，使用改进的专家评分方法对其进行评判，具体计算公式：

(1)

式中Xi为专家组评价值，λi为权威系数，ci为单项评估指标评价值。

定量指标数据是根据城乡供水规划报告和水厂提供资料直接选用，但是各数据量纲不同，因此，需要对其使用直线型无量纲化处理。

正向评估指标：

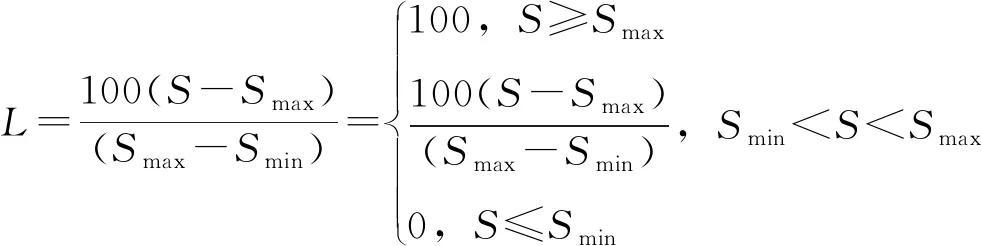
(2)

逆向评估指标：

(3)

式中S为量纲数实际值，Smax为量纲数实际值最大值，ci为量纲数实际值最小值，L为定量评估指标评价值。

1.3 评估指标权重计算法

1.3.1AHP法权重计算

美国运筹学家Saaty 20世纪提出AHP法处理各类决策性问题的方法，广泛应用于各类学科，方法具有简单、实用性[11-13]。考虑各个城乡供水一体化工程评估要素，采用要素之间互相比较的标度法(见表1)。

表1 各评估要素重要性比较

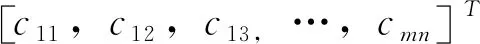
1.3.2熵权法权重计算

熵权法主要用于对不确定性信息的量度，已被广泛用于各学科决策评估过程[14-16]。根据不同专家组对评估指标的评估成果，收集形成原始资料矩阵K=(kij)m×n，根据评估指标属性，考虑各评估指标不同，对其进行归一化处理得到矩阵X=(xij)m×n，进而求得评估指标的熵值，具体见公式(4)(5)：

(4)

式中Xij表示第i个专家对第j个评估指标的评估值。

(5)

式中Gj表示计算评估指标的熵值。

但是，当θij=0时，需对其进行修正，此时θ计算公式为：

(6)

1.3.3AHP—熵权法组合赋值权重计算

AHP—熵权法组合赋值权重计算方法，是结合AHP和熵权法将二者计算所得权重值融合计算，结合两者方法的优缺点，同时兼顾模型的主观性和客观性[17-18]。若假定AHP法和熵权法分别已计算获得模型评估指标权重值。

AHP法权重列向量：

Yi=(yi1，yi2，yi3，…，yim)T

(7)

式中Yi表示计算评估指标的AHP法计算值。

熵权法权重行向量：

Pi=(P1，P2，P3，…，Pm)

(8)

式中Pi表示计算评估指标的熵权法计算值。

组合权重评估指标为：

(9)

式中Ui表示AHP-熵权法综合评估权重值。

根据城乡供水一体化模型特点，计算模型最大隶属度，将模型评估成果分为3种等级，评估计算成果超过0.90分以上属于安全，0.7～0.9分属于基本安全，低于0.7属于不安全。

2 城乡供水一体化模型应用

2.1 研究区域

永泰县隶属于福州市，位于闽东地区，区域内水系发达，大樟溪横贯整个县城，长约121 km，流域面积为1 786 km2，一级支流24条，年平均水资源总量约40多亿m3，截止2016年底，县内已建成水源工程866处，民政部注册农民用水协会88个，人均占有水资源1.2万m3，山区面积为847 km2，丘陵面积为1 394 km2，地形复杂，工程修建相对困难，是福建省少数的贫困县，属于典型的城乡供水不平衡县城。由此，2019年以后永泰县政府推进城乡供水一体化饮水安全工程，有效改善当地居民饮水现状。因此，本次模型将永泰县城乡供水一体化工程作为研究区域，对其城乡供水一体化工程进行深度评价，检验模型实用性和适用性。

2.2 评估指标

将城乡供水一体化定义为具有系统，并将其中影响因素整合归类，使得各层级之间相互关联使用定性和定量两项评估指标展开研究，再根据层次性进行整体归类，形成城乡供水一体化模型评估指标，再构建判断矩阵分别计算权重值。鉴此，本次模型划分为3层，分别为目标层、准则层以及方案层依次递进(见图1)。

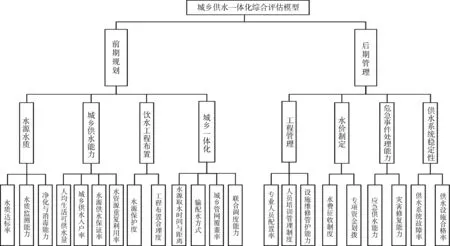
图1 城乡供水一体化评估模型示意

根据城乡供水一体化内涵，模型集中于城乡供水一体化工程的前期规划和后期管理。前期规划着重于城乡供水一体化能力，后期管理落点于城乡供水系统稳定性。因此，本次评估模型将评估指标划分为3层，其中1级评估指标8项，2级评估指标共22项评估指标。

2.3 模型应用

2.3.1AHP法权重计算

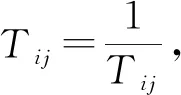
根据判断矩阵D矩阵结果使用方根法，将判断矩阵D同一行元素进行行内连乘，并开8次方，则对应层评估指标AHP法权重：

(10)

根据公式(10)计算求得，AHP法所对应的准则层权重(见表2)。

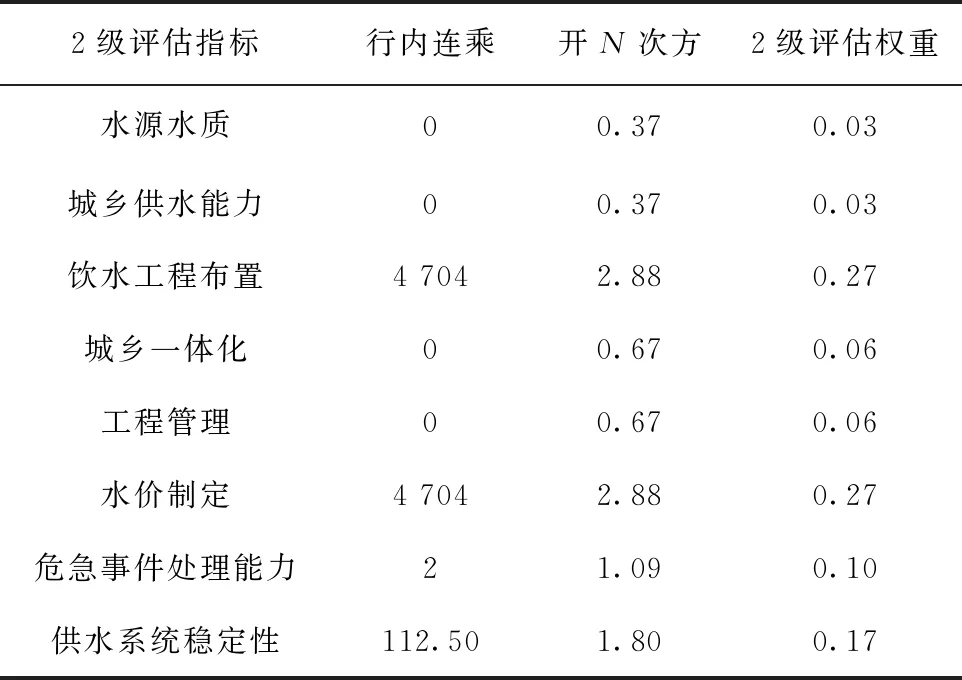
表2 永泰县城乡供水一体化AHP法权准则层权重值

将判断矩阵D88第i列Di行向量和权重Wj列向量进行矩阵相乘。依照矩阵相乘和权重计算成果，对应计算单个最大特征值λmax和对应特征向量α。

通过本次模型计算表明，评估权重系数最大特征向量λmax=8.05，一次性比率计算成果CI=(λmax-n)/(n-1)=0.01小于0.1(见表3所示)，因此，本次准则层判断矩阵符合一致性要求，同理可知，通过对方案层判断矩阵计算成果，判断矩阵符合一致性要求，并计算获得方案层AHP法计算权重Wj，再乘以所对应准则层权重，求得AHP最终权重为：

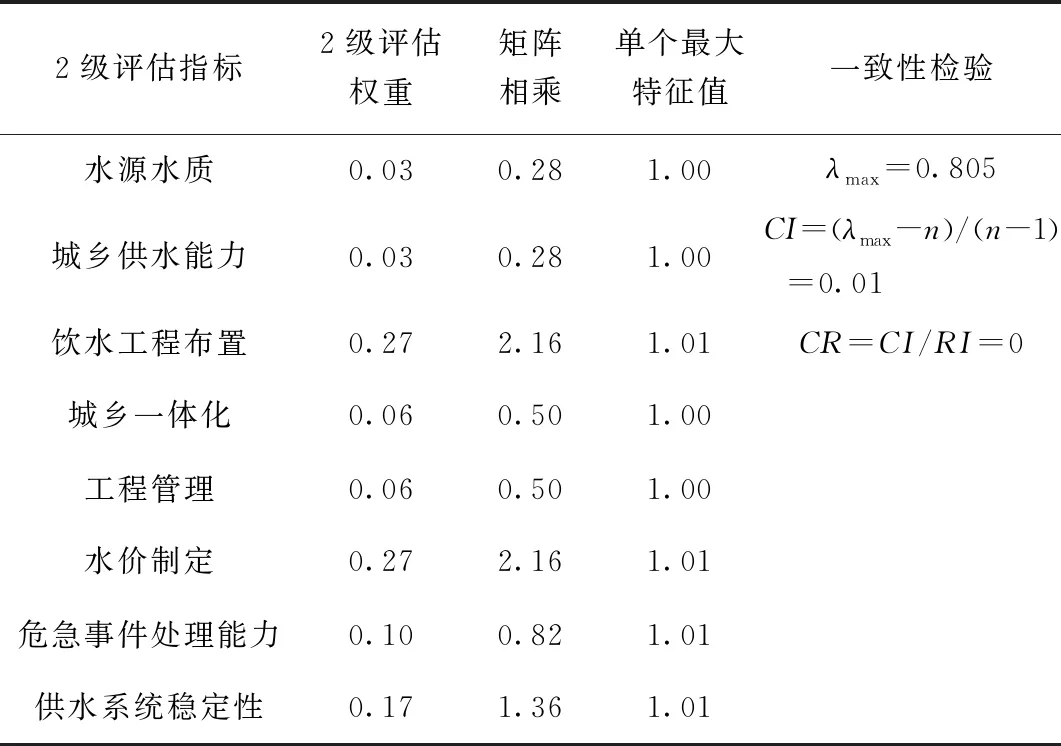
表3 永泰县城乡供水一体化准则层一致性检验

W=[0.01 0.01 0.00 0.00 0.01 0.01 0.02 0.03 0.23 0.01 0.01 0.03 0.01 0.01 0.04 0.02 0.13 0.13 0.03 0.08 0.02 0.15]

2.3.2计算熵权值

专家组按评估内容按照图1所示评估指标进行对永泰县城乡供水一体化方案评估打分，再依据不同专家组评估成果，基于对评估成果进行归一化标准处理，根据公式(1)～(3)形成归一化矩阵X88:

根据归一化矩阵X88，将X88每个元素根据公式(4)～(6)分别计算获得计算评估指标的熵值G8：

G8=[0.04 0.09 0.09 0.04 0.09 0.08 0.02 0.03 0.03 0.10 0.04 0.01 0.06 0.02 0.04 0.02 0.01 0.05 0.01 0.03 0.11 0.01]

2.3.3组合赋值权重计算

已知AHP计算获得权重为D88，而熵权法计算获得熵值G8，根据公式(7)～公式(9)通过将AHP法权重列向量D1和熵权法权重行向量G8相乘获得AHP-熵权法综合评估权重值Ui。

Ui=[0.02 0.04 0.01 0.00 0.02 0.02 0.01 0.03 0.21 0.02 0.02 0.01 0.03 0.00 0.06 0.01 0.03 0.21 0.01 0.09 0.08 0.05]

2.3 模型计算成果

永泰县属于典型经济相对落后区域，城区内水资源相对丰富，但城区工程布置艰难，人均占有水量偏低，城乡供水差距较大。考虑永泰县区域状况，本文结合永泰县供水现状，建立永泰县城乡供水一体化模型，分别运用AHP法和熵权法计算获得不同评估指标的计算结果，再通过使用AHP—熵权法组合赋值计算权重(见表4)。

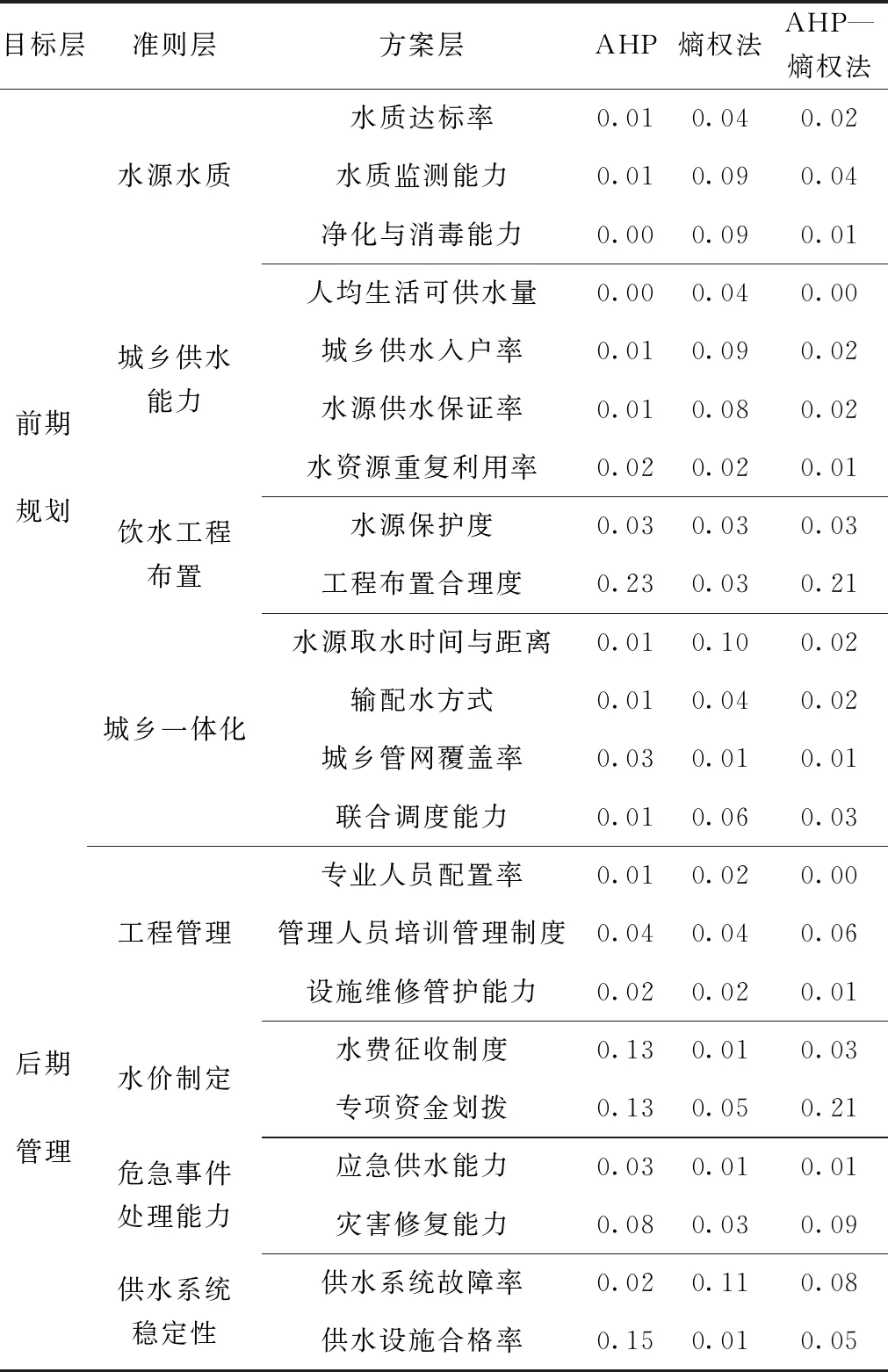
表4 永泰县城乡供水一体化模型计算成果

本次模型分析多个要素之间的联系，其计算隶属度为0.769 0，其隶属度位于0.7～0.9之间，则综合评价结果为中等，符合城乡供水一体化饮水安全评估要求。通过模糊评估计算表明，工程布置合理度和专项资金划拨权重为0.21，其权重值在所有评估指标占比最大，人均生活可供水量、专业人员配置率权重值接近于0，是所有评估指标占比最小，以上结果表明永泰县城乡供水一体化评价体系易受到工程布置和资金划拨影响，而人均生活可供水量、专业人员配置率影响程度相对较小。更深入分析，主要因永泰县地处山区，工程布置合理和资金落实两要素是制约工程发展的两大主要条件，鉴于此，建议本次永泰县城乡供水一体化要统筹安排资金进度，跟进资金落实情况，工程方案布置注重水源点布置，管道设置和水闸尺寸等工程措施，应进行多方论证方可实施。

3 结语

城乡供水一体化是当前研究热点，有利于缩小城乡差距，有利于提高城乡水资源的合理利用，是符合当前城乡建设的时代要求。然而，城乡供水一体化不仅仅考虑城市或者考虑乡村，而是需要将城市和乡村各种因素列入考虑范畴，若仅仅使用单独AHP法、熵权法的评估模型不能准确评估城乡供水一体化，造成评估结果不准确，评估内容不完善。鉴于此，本文采用AHP～熵权法组合赋权计算城乡供水一体化模型权重，更深入剖析影响城乡供水一体化影响因素。通过模型计算表明，城乡供水一体化要兼顾城乡应急供水和供水稳定性，即保证城乡供水稳定，同时，要使得供水系统具有应急供水能力。综上，本文使用的AHP～熵权法结合了主观性和客观性两大重要条件，构建的城乡供水一体化模型符合城乡供水一体化工程要求，可准确、清晰对区域城乡供水一体化工程进行全面评估。