基于启发式搜索算法的无人机航迹快速规划

吴玉文， 牛智越， 韩倩倩

(北京物资学院信息学院,北京 101149)

随着社会的不断发展,无人机的应用范围越来越广[1]。无人机导航是按照要求的精度,沿着预定的航线,把无人机从出发地引导至目的地完成任务。目前无人机主要采用的导航技术有惯性导航、卫星导航、地磁导航和地形辅助导航等[2]。由于现有导航技术无法完全保证对无人机的精准定位,故存在部分精度误差。定位误差是一种常见的精度误差,在无人机常采用的惯性导航技术中就存在该误差[2],它是由于无人机在飞行时无法对自身精准定位而随时间累积的累积误差,包括垂直误差和水平误差。目前,为了提高导航性能进而降低导航误差,常见的解决方法是把惯性导航技术与其他导航技术组合使用。但是在恶劣的条件下,只能采用惯性导航技术,通过在飞行区域设置的校正点实时校正定位误差,使得无人机校正误差后按照预定航线到达目的地[3]。因此,要解决的航迹规划问题是在只能使用惯性导航技术的条件下,在已知出发地、目的地的位置和校正点的类型、位置信息的基础上,从起始点出发,确定无人机所经过的校正点类型以及校正点连接顺序,使其在满足校正定位误差约束的前提下成功到达目的地,同时使得规划的无人机航迹长度最短。

近年来学者们对无人机航迹规划问题的研究主要集中在威胁规避、任务要求与性能限制等方面,对于定位误差与航迹规划两者结合考虑的研究较少。尹高扬等[4]在航迹规划中同时考虑了无人机的航迹生成约束和地形信息,应用快速扩展随机树进行了航迹规划。张亚兰等[5]提出离线规划和在线避障两者结合的航迹规划方法,分别应用双向A*算法和向量场直方图算法来实现。李世晓等[6]研究了带有威胁、任务战术等多约束条件下的航迹规划问题,应用改进的A*算法进行求解。方群等[7]、Goez等[8]通过考虑威胁区域和任务的侧重程度,应用改进粒子群算法来提高航迹规划的求解质量。许江波等[9]通过考虑威胁区域、无人机性能要求以及转弯代价等方面,改进了人工鱼群算法进行问题求解。李文广等[10]考虑了无人机最小转弯半径,通过证明得出了最优的转弯策略,并将其结果应用到航迹规划中。刘世一等[3]首次将定位误差与航迹规划两者结合考虑,建立了机载惯导系统误差模型和光电侦察载荷校正模型来减小航迹的误差,并提出在规划航线上设置校正点进行误差校正。

在已知校正点的类型、位置坐标以及可校正的误差范围的情况下,考虑飞行过程中无人机的累积误差对有效航迹长度的影响,建立了考虑定位误差的无人机航迹规划模型,设计了启发式深度优先搜索+回溯算法对模型进行快速求解,最后对解的结果做了进一步的优化改进。

1 考虑定位误差的航迹快速规划问题

1.1 问题描述

已知某无人机需要从出发点到达目的地快速规划出一条航迹,A为航迹起始节点,B为航迹终止节点。从A点出发时,无人机的水平误差和垂直误差均为0。无人机每飞行1 m,垂直误差和水平误差将各增加δ个单位。因此飞行区域中有若干垂直校正点和水平校正点对其定位误差进行校正,各节点(包括起点、终点与校正点)的位置与类型均已知。

当无人机到达某垂直校正点时,若垂直误差不大于α1个单位,水平误差不大于α2个单位,则对其进行垂直误差校正。校正后,其垂直误差变为0,水平误差保持不变。当无人机到达某水平校正点时,若垂直误差不大于β1个单位,水平误差不大于β2个单位,则对其进行水平误差校正。校正后,其水平误差变为0,垂直误差保持不变。若无人机到达B点时其垂直误差和水平误差均应小于θ个单位,则认为航迹规划成功。如何规划航迹才能使无人机从起始点A出发,以最短的距离准确地飞到目的地B？

1.2 模型建立

1.2.1 符号说明

H:垂直校正点集合。

L:水平校正点集合。

S:所有节点集合,S=H∪L∪{A}∪{B}。

(ai,bi,ci):节点i的空间坐标。

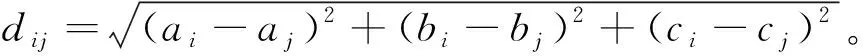
决策变量:

hi:无人机在节点i处的垂直误差,其中hA=0。

li:无人机在节点i处的水平误差,其中lA=0。

1.2.2 约束条件

根据不同节点约束条件的不同,校正约束与航迹约束可分为4类。

第1类从A点进入校正点j的误差约束。式(1)表示从起点A飞入校正点j的垂直误差约束,式(2)表示从起点A飞入校正点j的水平误差约束。具体含义为:若节点j为垂直校正点,无人机到达j点时垂直误差不大于α1,水平误差不大于α2。若节点j为水平校正点,垂直与水平误差分别不大于β1与β2。

xAjdAjδ≤(1-rj)α1+rjβ1,j∈H∪L

(1)

xAjdAjδ≤(1-rj)α2+rjβ2,j∈H∪L

(2)

第2类从校正点i飞入校正点j的误差约束。式(3)表示飞入校正点j的垂直误差约束,式(4)表示飞入校正点j的水平误差约束。式(5)表示飞入校正点j后垂直误差的值,式(6)表示飞入校正点j后水平误差的值。

hiri+xijdijδ≤(1-rj)α1+rjβ1,i,j∈H∪L

(3)

li(1-ri)+xijdijδ≤(1-rj)α2+rjβ2,

i,j∈H∪L

(4)

hjxij=(hi+dijδ)rjxij,i∈H∪L∪{A},

j∈H∪L

(5)

ljxij=(li+dijδ)(1-rj)xij,i∈H∪L∪{A},

j∈H∪L

(6)

第3类从校正点i到达B点的误差约束。式(7)表示到达B点的垂直误差约束,式(8)表示到达B点的水平误差约束。式(9)表示从A点到达B点的累计误差约束。

xiB(hiri+diBδ)≤θ,i∈H∪L

(7)

xiB[li(1-ri)+diBδ]≤θ,i∈H∪L

(8)

xABdABδ≤θ

(9)

第4类航迹约束。无人机所经过的节点是连续的,即被选择的节点之间的连线是一条路。

(10)

(11)

(12)

1.2.3 数学模型

目标函数为最小化无人机航迹规划的长度:

(13)

因此,式(1)～式(13)给出了考虑定位误差的无人机航迹规划问题的混合整数规划模型。

2 算法设计

由于模型中对于误差校正的约束条件较多,且下一节点的选取是由上一节点的定位误差与校正点类型决定的。因此该问题的解空间属于未知深度的解空间树,很难在短时间内利用求解器对模型进行求解。根据该模型的特点,针对每个节点的约束条件,逐步进行节点探索。

深度优先搜索(depth-first search,DFS)算法[11-12]是沿状态树的深度方向进行搜索,直到找到解或者无法继续搜索,是一种盲目的搜索算法,适用于一个问题出现多个分枝以及如何选择分枝可以尽快到达目标点的情况。回溯算法[13]在包含所有解的解空间树中,从根结点出发搜索解空间树。算法搜索至解空间树的任一节点时,先判断该节点是否满足问题的约束。如果不满足,则跳过对以该节点为根的子树的搜索,逐层向其祖先节点回溯；否则,进入该子树继续搜索,从而减少解空间树中无效节点的搜索。

结合以上两种算法的优点,采用启发式DFS+回溯算法求解考虑定位误差的无人机航迹快速规划问题。当解空间很大时,将DFS算法与启发式算法相结合,避免DFS算法进行盲目搜索,从而更快地到达目标点。而在对节点进行分枝的过程中,根据约束条件,DFS算法可能会在某些节点处无法继续搜索,找不到符合约束条件的下一节点。回溯算法能很好地解决DFS算法在搜索时找不到可行节点的问题,从而避免搜索失败。因此,在无人机航迹规划问题中应用启发式DFS+回溯算法可以快速找到近似最优解,规划出无人机航迹。

启发式DFS+回溯算法使用3个列表,开放列表Open、节点列表Jiedian与删除列表Shanchu,分别储存当前待分析节点、已规划的飞行节点和无效飞行节点。应用该算法时的操作步骤如下,算法流程如图1所示。

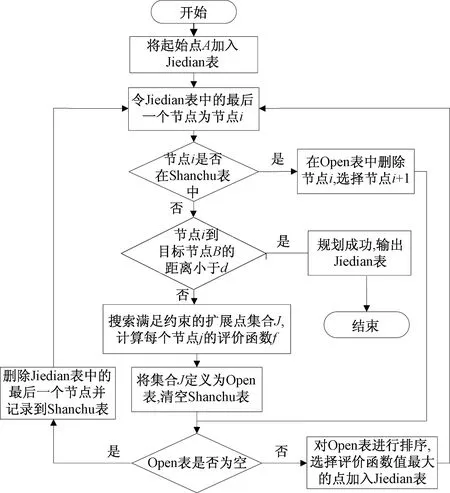
图1 算法流程Fig.1 Flowchart of algorithm

步骤1开始将起始点A放入Jiedian表,令Shanchu表为空。

步骤2令Jiedian表中最后一个点为节点i,判断当前节点i是否在Shanchu表中。若节点i不在Shanchu表中,转步骤3；否则在Open表中删除节点i后,选择节点i+1,转步骤5。

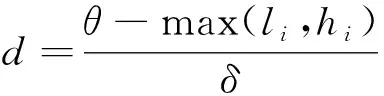
步骤4以L为搜索步长,L=max{α1,α2,β1,β2},以当前节点i与目标点B向量方向为轴,以ω偏向角绕轴旋转进行搜索,搜索区域如图2所示。在图2中,无人机每次的搜索区域是一个类锥体区域,类锥体区域内每一个满足约束条件的节点j组成集合J。计算集合内每个节点的评价函数值fj,其中fj=cos{∠jiB},j∈J。将集合J中所有元素加入Open表,清空Shanchu表。

图2 无人机搜索区域Fig.2 Search area of the UAV

步骤5判断Open表是否为空。若为空,则执行回溯算法,即删除Jiedian表中的节点i并记录到Shanchu表,转步骤2；否则转步骤6。

步骤6对Open表中节点的评价函数值进行排序,选择值最大的点j作为下一个航迹节点。把该节点j加入Jiedian表,转步骤2。

3 算例分析

3.1 算例数据

已知某飞行区域内共规划部署了611个校正点,其中各校正点的空间坐标、校正类型以及起点与终点的空间坐标均为已知的,飞行区域节点信息如表1所示,由于节点较多,表1只列举了部分节点的信息。设定α1=25,α2=15,β1=20,β2=25,θ=30,δ=0.001,ω=90°。

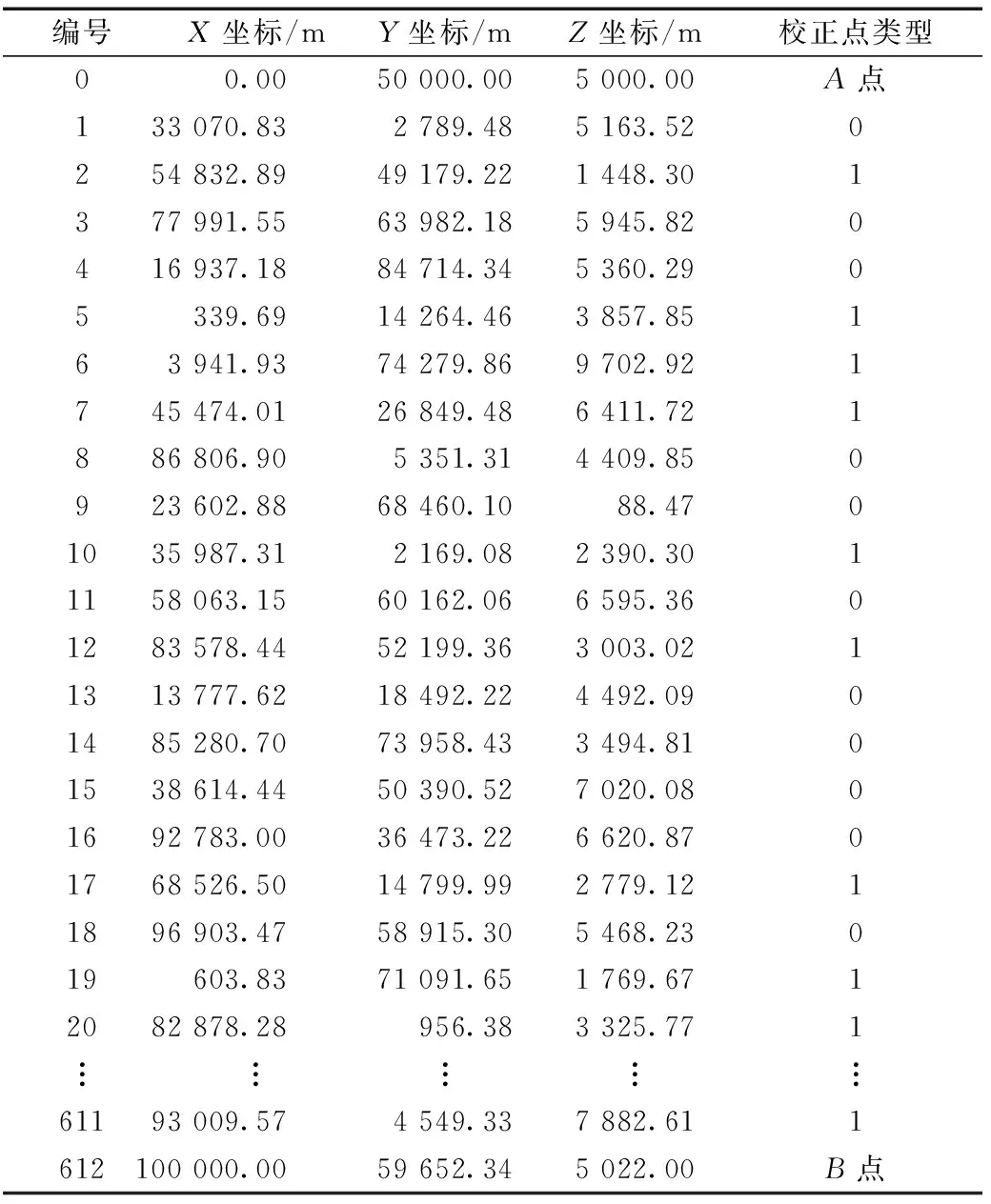
表1 飞行区域节点信息Table 1 Node information of flight area

3.2 算例结果

根据本文的算法,利用MATLAB 2014b编程,在Intel(R)Core i5-6200U @ 2.30 GHz 2.30 GHz处理器上运行程序,经过0.059 s得出近似最优解,无人机从A点出发,经过8个校正点,飞行106 350.061 m后,到达B点。经过的校正点编号和类型以及校正前的误差如表2所示,规划出的路径图如图3所示。

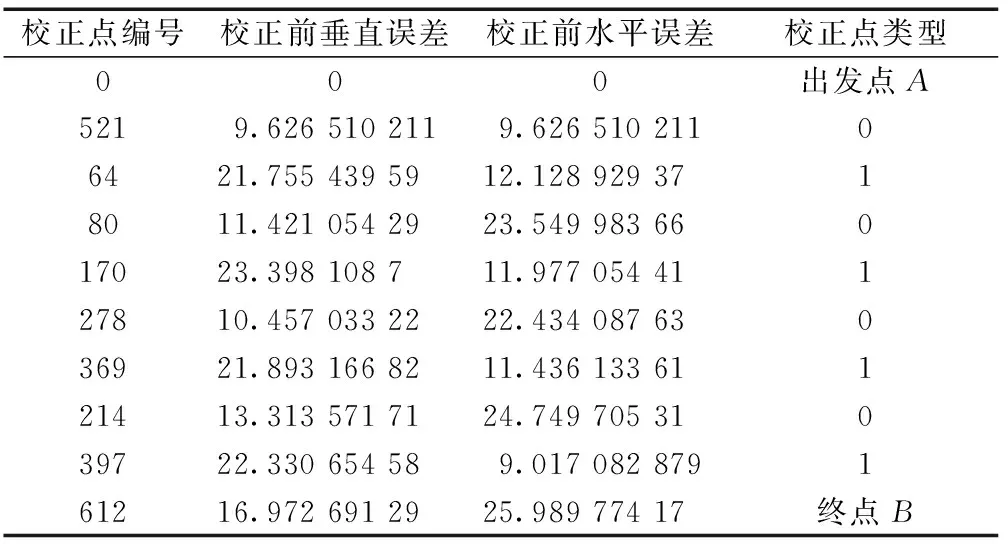
表2 航迹规划结果Table 2 Path planning results

为验证本文算法在性能上的优势,利用表1的数据,对比A*算法,在相同处理器配置的计算机上运行算法的验证,两种算法结果对比分析如表3所示。

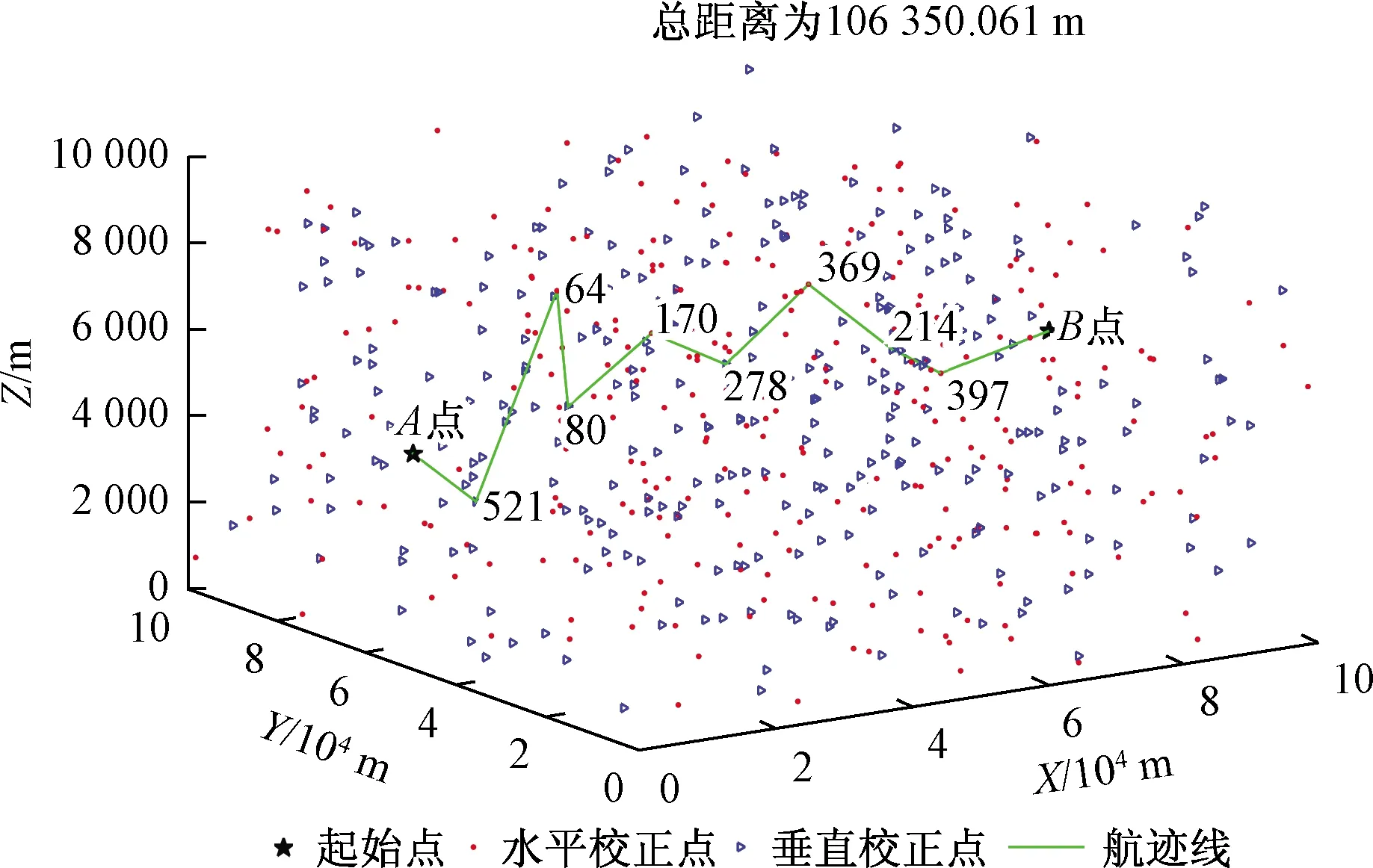
图3 航迹规划图Fig.3 Path planning map

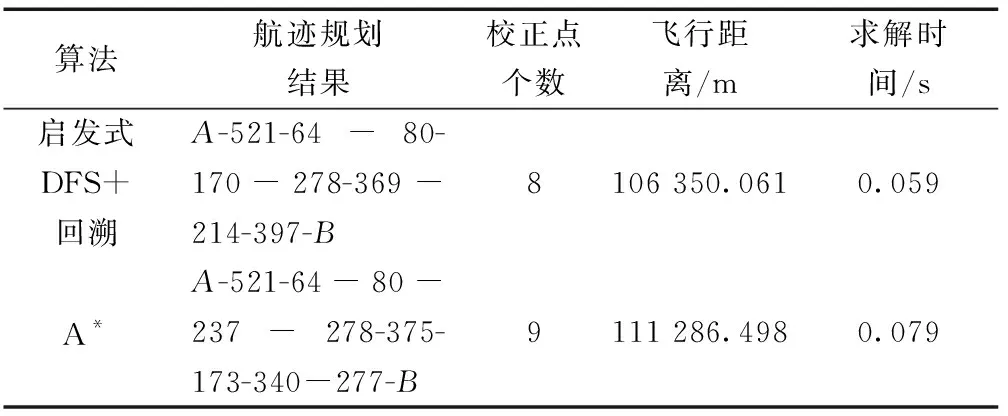
表3 算法结果对比Table 3 Results comparison of algorithms

由表3可见,启发式DFS+回溯算法可以得到更好的解,其飞行距离比A*算法减少了4 936.437 m,经过的校正节点少1个,且求解时间更短。

3.3 求解结果优化

由于启发式DFS+回溯算法可以快速求得一个较好的可行解,却不能保证该解的全局最优性。为了提高解的质量,引入模拟退火的思想,即在由启发式DFS算法搜索得到的每一步的领域结构解空间中,以一定概率的方式接受评价函数值变“差”的解。随着启发式DFS算法探索深度的增加,无人机与目的地距离的减少,接受差解的概率随之逐渐减小。每一步搜索后选择的解xq由以下方法获得。

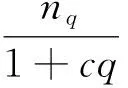
(14)

I：U(1,M)

(15)

xq=arg[Open(q)(I)]

(16)

式中：q是搜索步数；nq是第q步所产生的Open表中的元素个数；xq是第q步选择的解；c为参数,在区间[0.1,0.9]内取值；经多次实验,取0.4作为c的取值。式(14)表示第q步在Open表中排序后选择解空间的范围值；式(15)表示在服从均匀分布的区间[1,M]中随机产生一个索引I；式(16)表示在排序后的Open表中选择第I个评价函数值f对应的解xq。

根据式(14)～式(16)的优化操作,将表1中的数据按照启发式DFS+回溯算法进行优化迭代计算,其优化迭代结果与航迹规划结果如图4和图5所示。由图4可知,随着优化迭代次数的增加,算法能不断地找到最优解,最后结果逐渐趋于稳定。

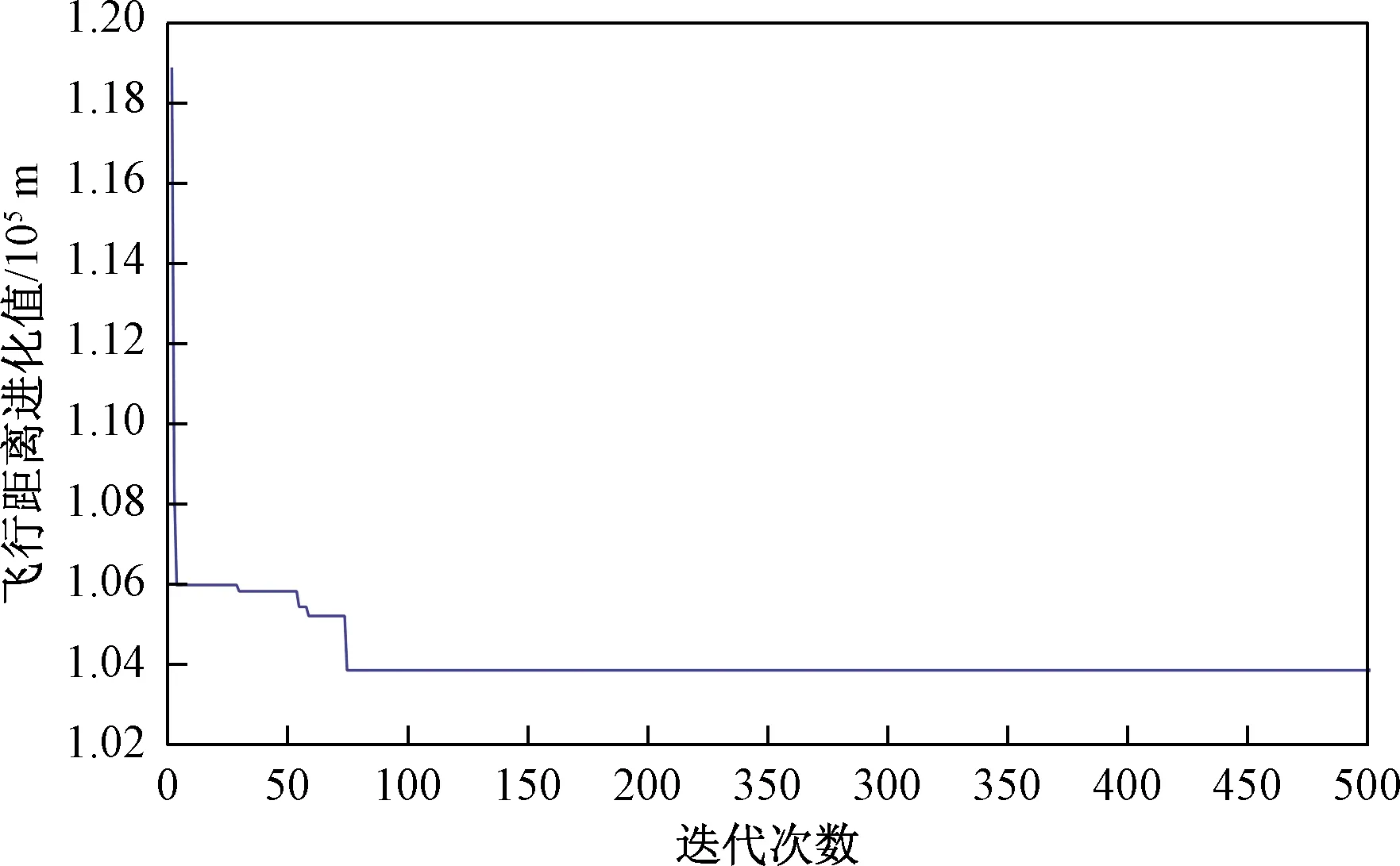
图4 优化迭代结果Fig.4 Results of optimization iteration

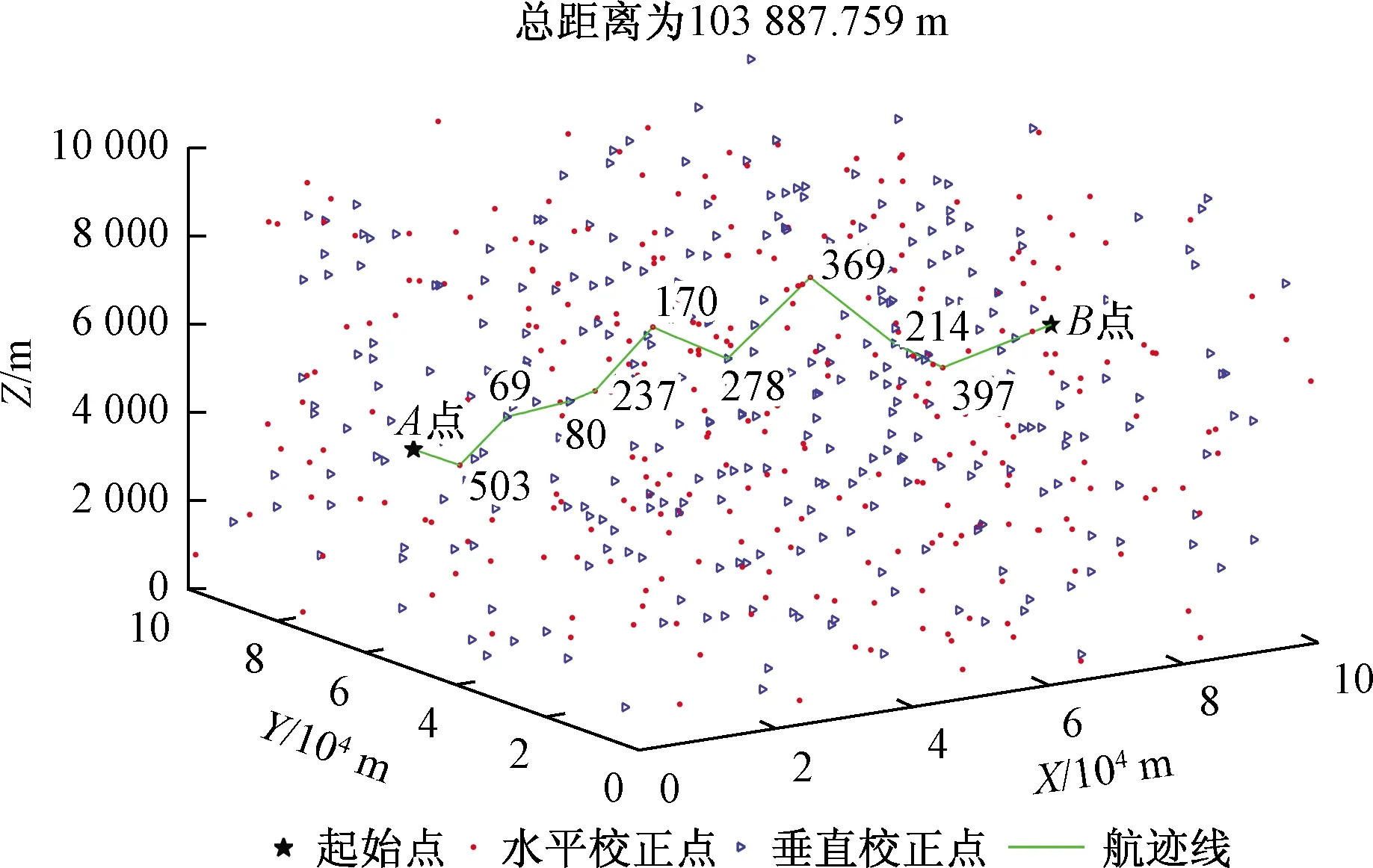
图5 优化后的航迹规划图Fig.5 Optimized path planning map

从图5的航迹规划结果来看,无人机的航迹更加趋于平滑,与之前的航迹规划结果相比,没有出现较大的飞行爬升和俯冲。这是因为在初始阶段的解空间中,解的评价函数值相差并不大,选择非最优评价函数的值可以跳出局部最优解,使得航迹距离最短,航迹更平滑。

对3种算法的求解结果进行比较分析,结果如表4所示。通过对比发现,在航迹距离方面,加入模拟退火机制的启发式DFS+回溯算法求解出的航迹距离最短,其长度为103 887.759 m,比启发式DFS+回溯算法节省了2 462.302 m,比A*算法节省了7 398.739 m。在求解时间方面,由于加入模拟退火机制,优化后的启发式DFS+回溯算法求解时间相对较长,这是因为该算法的求解时间与迭代次数有关。可以根据实际要求对该算法的迭代次数进行调整,在求解的时间和求解精度之间取得较满意的求解效果。

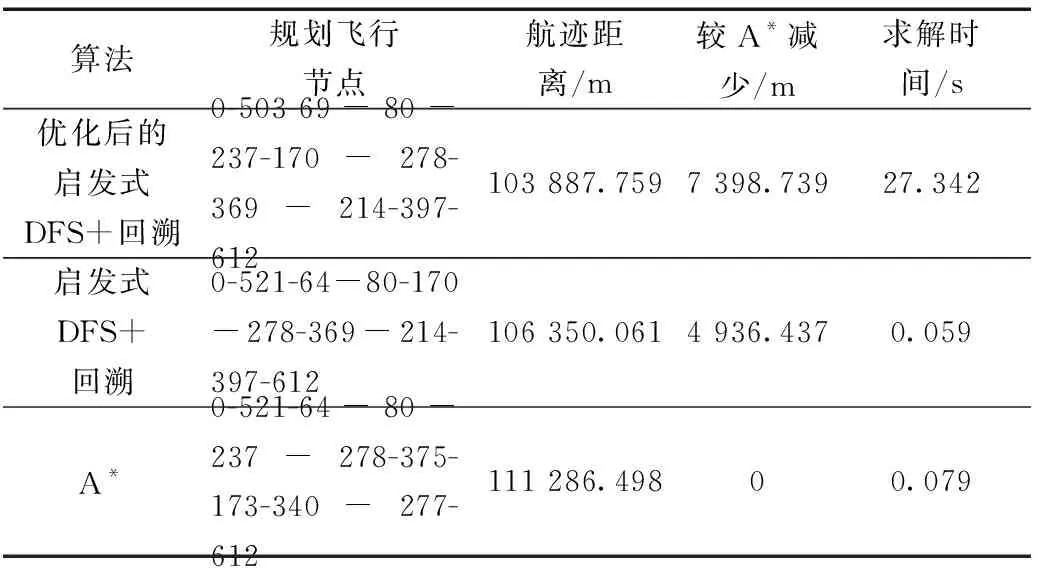
表4 算法比较分析Table 4 Comparison and analysis of algorithms

4 结论

建立了考虑定位误差的无人机航迹规划的数学模型,设计了启发式DFS+回溯算法,解决了通过校正点不断校正定位误差的航迹规划问题,并在此算法的基础上进行了优化改进。实验结果表明,与A*算法相比,本文的启发式DFS+回溯算法在求解时间上具有一定优势,航迹距离结果更优。而加入模拟退火机制的启发式DFS+回溯算法虽然求解时间变长,但是求解质量更高。本文的模型与算法为无人机航迹快速规划问题的研究及应用提供了一定的理论依据。