连续搅拌反应釜的自适应模糊辨识与预测控制

许 娣， 高钰凯， 佃松宜

(四川大学电气工程学院,成都 610065)

化工生产过程中,由于很多原材料经处理后会改变其本身的物理或化学性质,具有易燃易爆的特性。因此,严格的参数和质量要求是确保生产和操作人员安全的重要指标。实际化工生产过程中受控对象的复杂性主要表现为非线性、多输入多输出、强耦合性、时滞性、不确定性等[1]。连续搅拌反应釜(continuous stirred tank reactor, CSTR)是化工生产过程中的常用反应设备,本身具有高度的非线性,由于难以获得高精度的数学模型,因此,采用传统理论设计控制器的方法难以满足精度和质量要求[2]。

1965年,Zdeh教授首次提出模糊集理论。模糊理论的出现极大程度上解决了工业控制领域的难题[3]。20世纪90年代初期,大量学者进行了许多非线性预测控制的相关理论和算法研究,并提出了多种非线性预测控制算法[4]。Hamdy等[5]结合Lyapunov函数建立了闭环T-S模糊双线性模型的稳定性条件,设计一种模糊输出反馈控制器,通过CSTR仿真证明该算法具有较好的控制效果。张明财等[6]基于无模型自适应控制算法和PCS7设计了CSTR温度自控系统,该系统能够模拟实际工业现场运行,所设计的控制器具有较好的抗干扰和实用性。何美霞等[7]采用动态矩阵控制(dynamic matrix control，DMC)算法对非线性CSTR反应器的温度进行控制,即使是在干扰和模型适配的情况下,仍可快速跟踪期望目标。Boulkaibet等[8]将聚类算法与核岭回归(kernel ridge regression, KRR)算法相结合来获取CSTR的模糊模型,最后采用广义预测控制算法来实现模糊预测控制。

根据CSTR系统的非线性特征以及采集到的数据集,将模糊划分C均值聚类算法与分层遗传算法相融合,辨识得到CSTR系统T-S模糊模型的前件参数,并采用自适应机制遗忘因子递推最小二乘法对模型的后件参数进行估计,即采用辨识算法来获得CSTR系统的T-S模糊模型。最后,基于该模糊模型对CSTR进行自适应模糊广义预测控制器的设计。仿真结果表明,根据该辨识算法建立的CSTR的T-S模糊模型精确度较高,同时,预测控制器具有较强的抗干扰能力。

1 基于辨识算法的T-S模糊模型

1.1 T-S模糊模型

Takagi和Sugeno于1985年提出了T-S模糊模型[9]。T-S模糊模型采用IF-THEN形式来近似非线性系统。其中,每一条规则均代表了一个线性子系统[10]。通常情况下,非线性系统可通过以下形式来描述[11]:

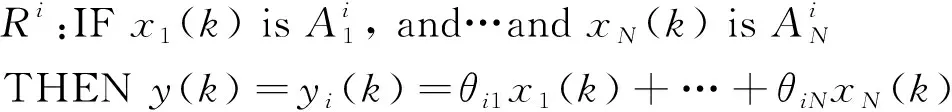
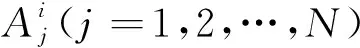
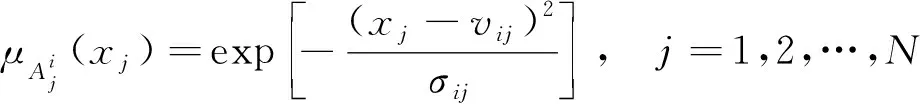
式(2)中：vij和σij分别表示隶属函数的中心和宽度,属于T-S模糊模型的前件参数。

为简化T-S模糊模型线性环节的表达形式,做以下替换:

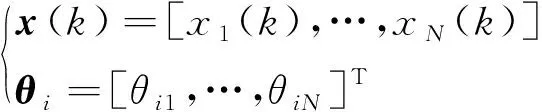
则式(1)中y(k)可表示为

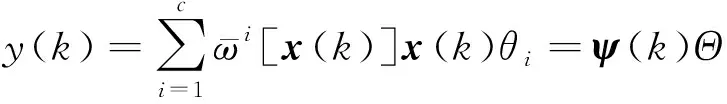
式(4)中:

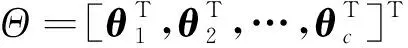
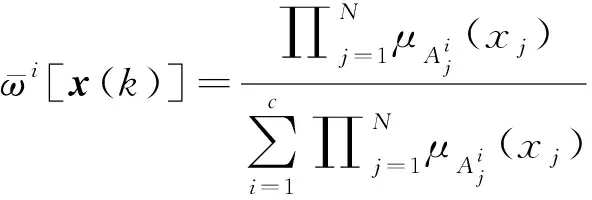
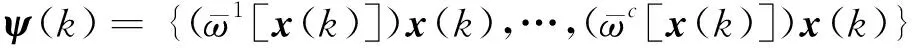
1.2 模糊划分C均值分层遗传算法

由于模糊C均值(fuzzyC-means,FCM)算法易陷入局部最优,而遗传算法(genetic algorithm, GA)能够对群体中的许多个个体进行同时处理,即有效地评估多个可行解,避免收敛于局部极小值[12]。因此,提出模糊划分C均值分层遗传算法(hierarchical genetic algorithm with improved fuzzy partitions fuzzyC-means,HGA-IFPFCM),这一算法在原有的模糊划分C均值聚类(improved fuzzy partitions fuzzyC-means algorithm, IFPFCM)算法的基础上融合了分层遗传算法(hierarchical genetic algorithm, HGA),由IFPFCM算法得到模糊规则的模糊隶属度uij和初始聚类中心ci,再使用HGA算法中的遗传操作逐步对T-S模糊规则的前件参数进行优化,进而得到最优的分类结果。

1.2.1 模糊划分C均值聚类(IFPFCM)

将数据集X={x1,x2,…,xn}按照每一类均对应一个聚类中心ci进行划分后得到c类,将每个样本j属于某一类的隶属度定义为uij,对于每个单独的样本点xj,采用隶属度约束函数：

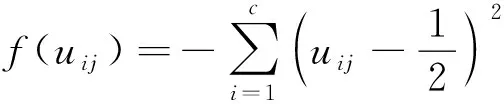
进而得到IFPFCM算法的目标函数：

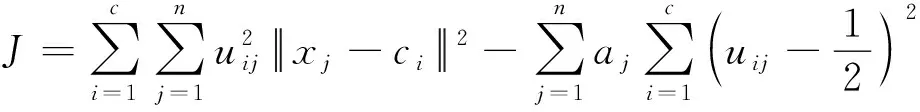
式(9)中：

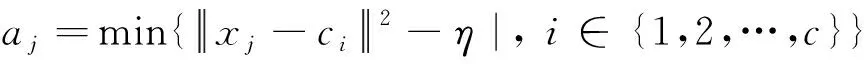
式(10)中:η为模糊度常数,一般取值为η=0.01～0.2。对式(9)采用拉格朗日乘数法:

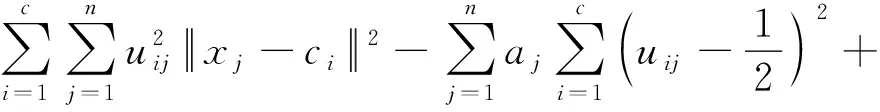
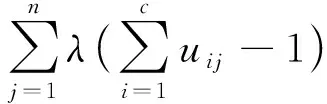
式(11)中：λ为拉格朗日乘子。对式(11)取极值后可逐步推导出隶属度uij和聚类中心ci的迭代公式。其中,隶属度uij的迭代公式为

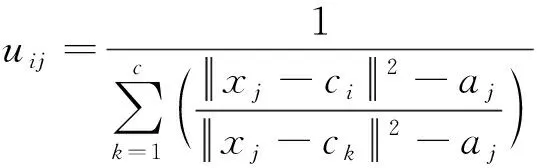
式(12)中:

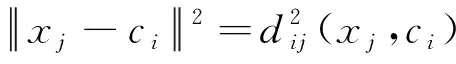
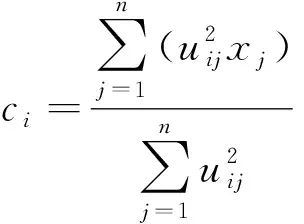
1.2.2 分层遗传算法(HGA)

GA算法是一种模拟生物遗传机制的全局收敛优化算法[13]。HGA算法是指对于一个具体问题,随机生成N×n个样本(N≥2,n≥2),随后将该样本分成N个均包含有n个样本的子种群,并且对这N个子种群均运行独立的GA算法,可记作GAi(1,2,…,N)。运行GA算法之后可得到HGA算法的初始层。

定义数组R[i,j](i=1，…，N,j=1，…，n)以及A[i](i=1，…，N),将N个子种群的GA算法连续迭代一定次数后,将遗传操作的结果种群以及与其相对应的平均适应度值分别记录到R[i,j]和A[i]中。HGA算法中的高层遗传步骤主要分为选择、交叉、变异以及替换。算法流程如图1所示。

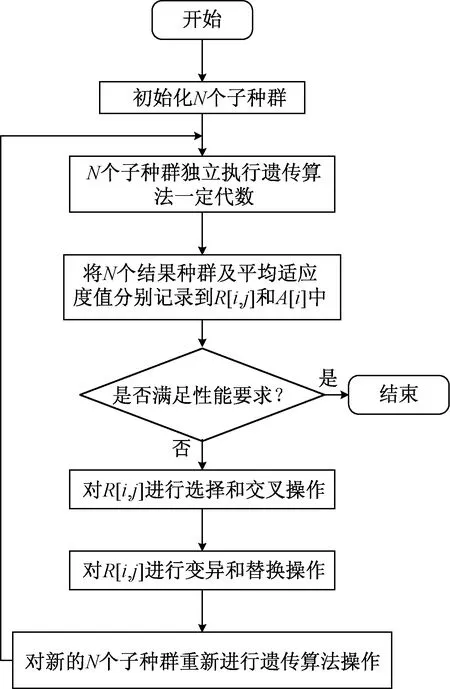
图1 HGA算法流程Fig.1 The flowchart of HGA

选择是指根据A[i]所代表的平均适应度值对数组R[i,j]进行择优选择。

交叉是指将群体中的各个个体随机搭配成对,当数组R[i,1，…，n]和数组R[j,1，…，n]被随机分配后,从位置x处进行交叉(1≤i,j≤N;1≤x≤n-1),则R[i,x+1，…，n]和R[j,x+1，…，n]相互交换对应部分,即交换GAi和GAj中的n-x个个体。

变异是避免HGA算法陷入局部最优的关键一步,主要是为了保持种群的多样性。在第二步进行交叉后,种群中的染色体发生变异,进而使得基因值发生改变[14]。

替换是指对于从数组R[i,j]中随机抽取的平均适应度值最弱的个体,HGA算法采用少量随机生成的新个体将其进行替换以形成新的种群,进而再次进行遗传操作。

以上4个步骤是HGA算法中高层遗传步骤的第一次迭代,当N个GAi各自执行遗传算法到一定的代数后,更新数组R[i,j]和A[i],并进行第二次迭代。如此进行循环遗传操作,直至取得满意的性能结果。

1.3 自适应机制遗忘因子递推最小二乘法

由于非线性系统本身的时滞等特性会对建模精度造成影响。因此,在T-S模糊模型的前件参数辨识算法的基础上,采用自适应机制遗忘因子递推最小二乘法辨识其后件参数。

对于每次迭代l,采用式(15)来更新式(3)中的参数估计向量θi[15]，即

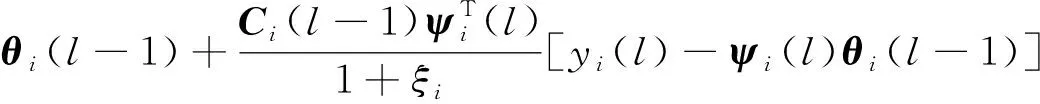
式(15)中：

Ci(l)是第i条模糊规则的协方差矩阵。

在每次迭代l中,协方差矩阵Ci(l)通过式(16)进行更新，即

Ci(l)=Ci(l-1)-

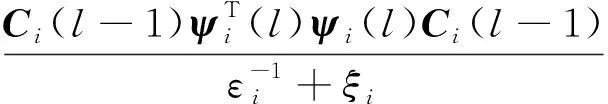
φi(l)=

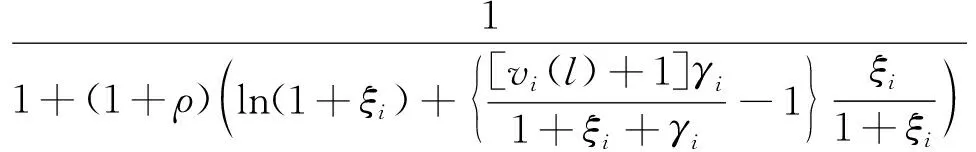
式(17)中：ρ是大于0的常数；vi(l)和γi分别为

vi(l)=φi(l-1)[vi(l-1)+1] (18)

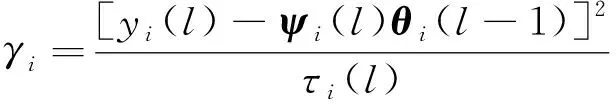
式(19)中：τi(l)可表示为

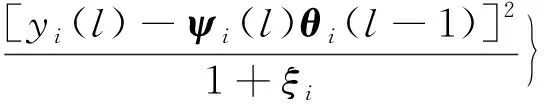
初始值φi(0)、vi(0)以及τi(0)的取值范围均为(0,1)。

2 自适应模糊广义预测控制

2.1 控制原理

自适应模糊广义预测控制(adaptive fuzzy generalized predictive control, AFGPC)主要包括了广义预测控制(generalized predictive control, GPC)的控制器、被控对象、T-S模糊模型及其参数调整4个部分。该控制系统集成了GPC算法、离线学习得到的T-S模糊模型以及通过自适应机制遗忘因子递推最小二乘法实现的模型参数在线调整。AFGPC的控制架构如图2所示[16]。

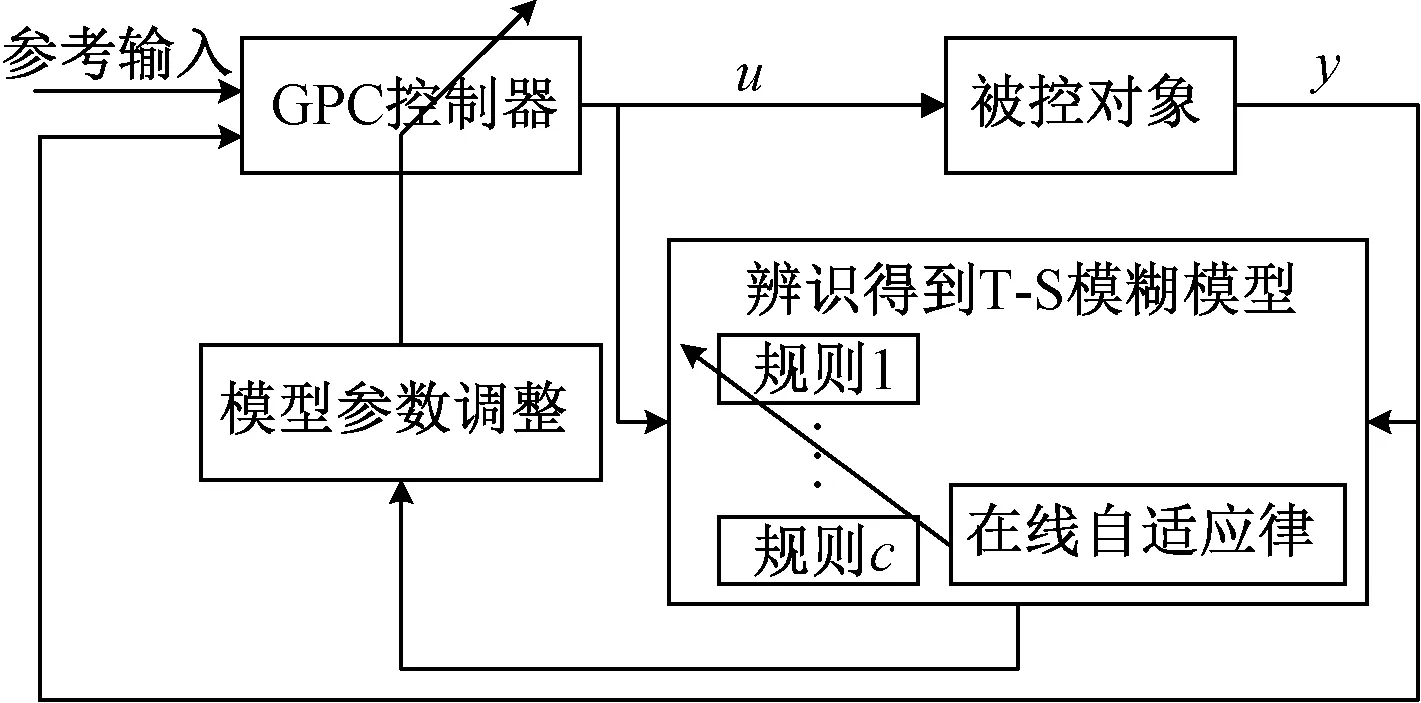
图2 AFGPC控制架构Fig.2 Thecontrol architecture of AFGPC

为研究方便,工业实践中的大部分非线性过程可通过式(21)来描述，即

y(k)=f[y(k-1),y(k-2),…,y(k-ny),

u(k-d-1),…,u(k-d-nu)] (21)

式(21)中：u(·)表示系统的输入；y(·)表示系统的输出；nu对应系统输入变量的阶次；ny对应系统输出变量的阶次；函数y(·)所描述的非线性系统可由式(22)表示的T-S模糊模型进行逼近，即

Ri:IFx1(k) isAi1, and…andxN(k) isAiN

THENyi(k)=ai(z-1)y(k-1)+

bi(z-1)u(k-d-1) (22)

式(22)中：Ri(i=1,2,…,c)表示第i条规则,c是模糊规则的个数；N=nu+ny;ai(z-1)和bi(z-1)具体为

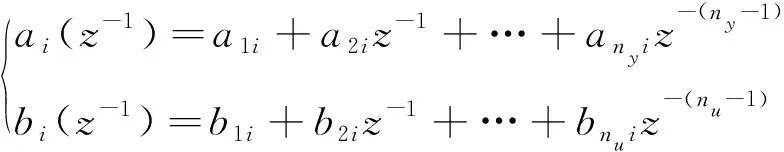
为保证后续控制律计算方便,根据1.1节,将向量x(k)=[x1(k),…,xN(k)]=[y(k-1),…,y(k-ny),u(k-d-1),…,u(k-d-nu)]以及向量θi=[a1i,…,anyi,b1i,…,bnui]T代入式(22),则y(k)可表示为

y(k)=

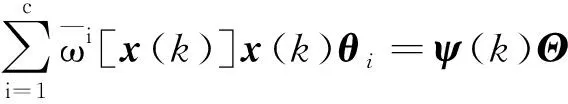
式(24)中:

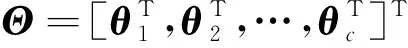
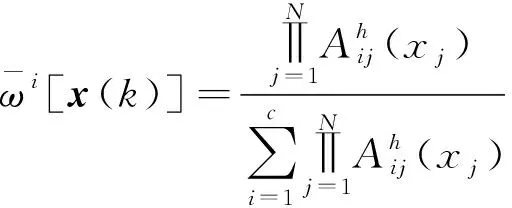
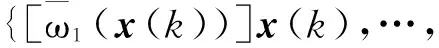
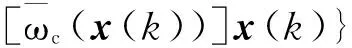
2.2 预测控制律

假设被控对象的离散数学模型为[17]

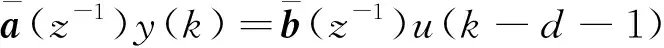
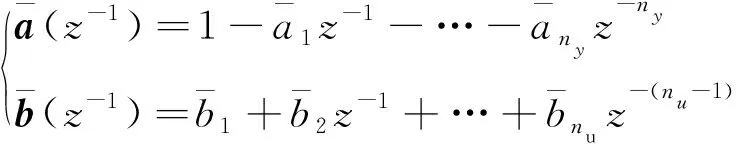
式(29)中:

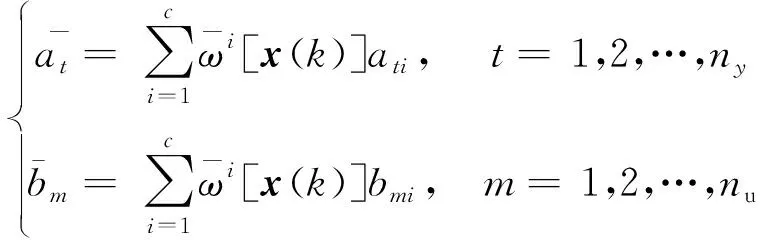
为得到AFGPC算法的预测控制律,取k时刻的优化性能指标函数为

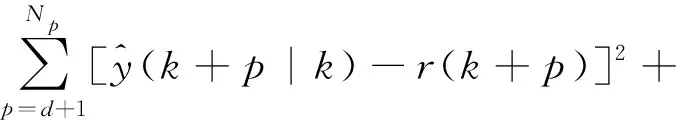
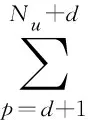
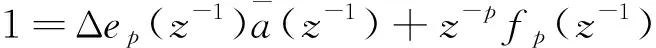
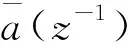
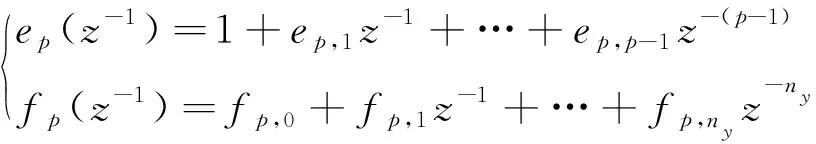
经推导可得：

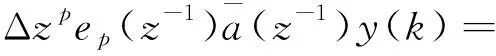
d-1) (34)

定义：

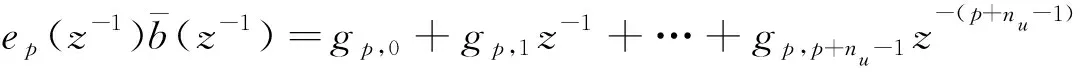
将式(32)和式(35)代入式(34)可得在k+p时刻的最佳预测值

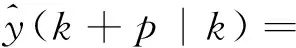
gp(z-1)Δu(k+p-d-1) (36)

即

y(k)=Gu(k)+F(z-1)y(k)+L(z-1) (37)

式(37)中:

根据推导得到的式(37),同时将式(31)中的λ(z-1)看作为常数,则AFGPC的优化性能指标函数式(31)可重新表示为

Jeq(k)=[Fy(k)+Gu(k)+L-R]T[Fy(k)+Gu(k)+L-R]+[λu(k)]2(38)

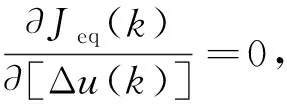
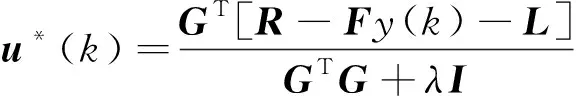
式(39)中：I是单位矩阵。控制过程中,将u*(k)的第一行作为控制信号输入给被控对象,Δu*(k)可通过式(40)得到。

Δu*(k)=K[R-Fy(k)-L] (40)

式(40)中：K是矩阵(GTG+λI)-1GT的第一行。

3 CSTR系统仿真验证

3.1 CSTR系统的数学模型

CSTR系统的反应是由原料A转化为产物B的非线性过程,其结构示意图如图3所示。

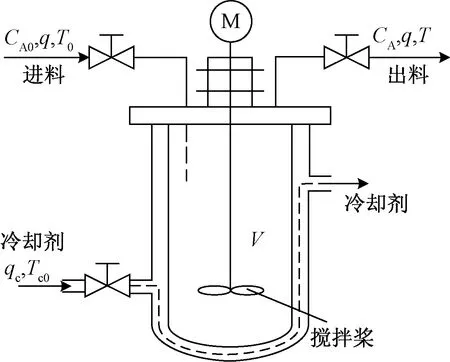
图3 CSTR系统结构示意图Fig.3 The schematic diagram of CSTR system structure

为得到CSTR的理想数学模型,假设反应器内部发生的是不可逆的放热反应,根据质量守恒和能量守恒定律,CSTR系统的数学模型可描述为[18]

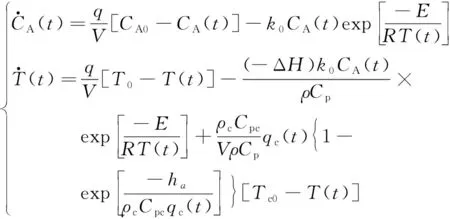
式(41)中的相关参数及其描述如表1所示。

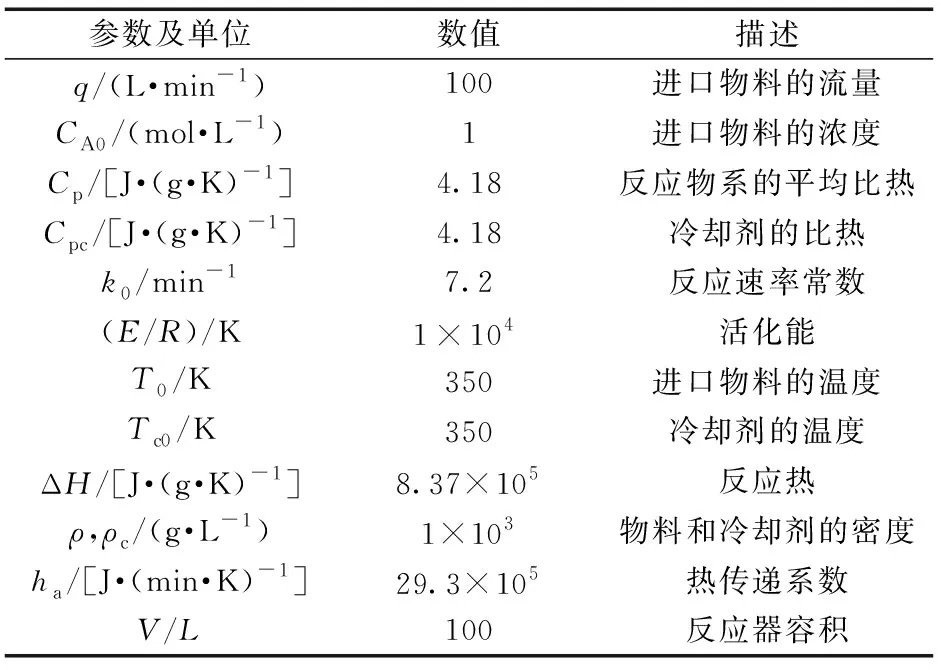
表1 CSTR系统的模型参数Table 1 Model parameters of the CSTR system

3.2 CSTR系统的模糊辨识

采用第1章中的HGA-IFPFCM算法和自适应机制遗忘因子递推最小二乘法来辨识CSTR系统的T-S模糊模型的前后件参数。

CSTR反应过程主要通过控制冷却剂流量qc(t)来调整出料浓度CA(t)。因此,输入和输出信号可分别表示为y(t)=CA(t)以及u(t)=qc(t)。根据现场设备实际运行情况,将控制信号qc(t)的范围设定为[90(L/min),110(L/min)],相应地采集1 000组数据。图4所示为用于采集数据集的控制信号变化曲线。

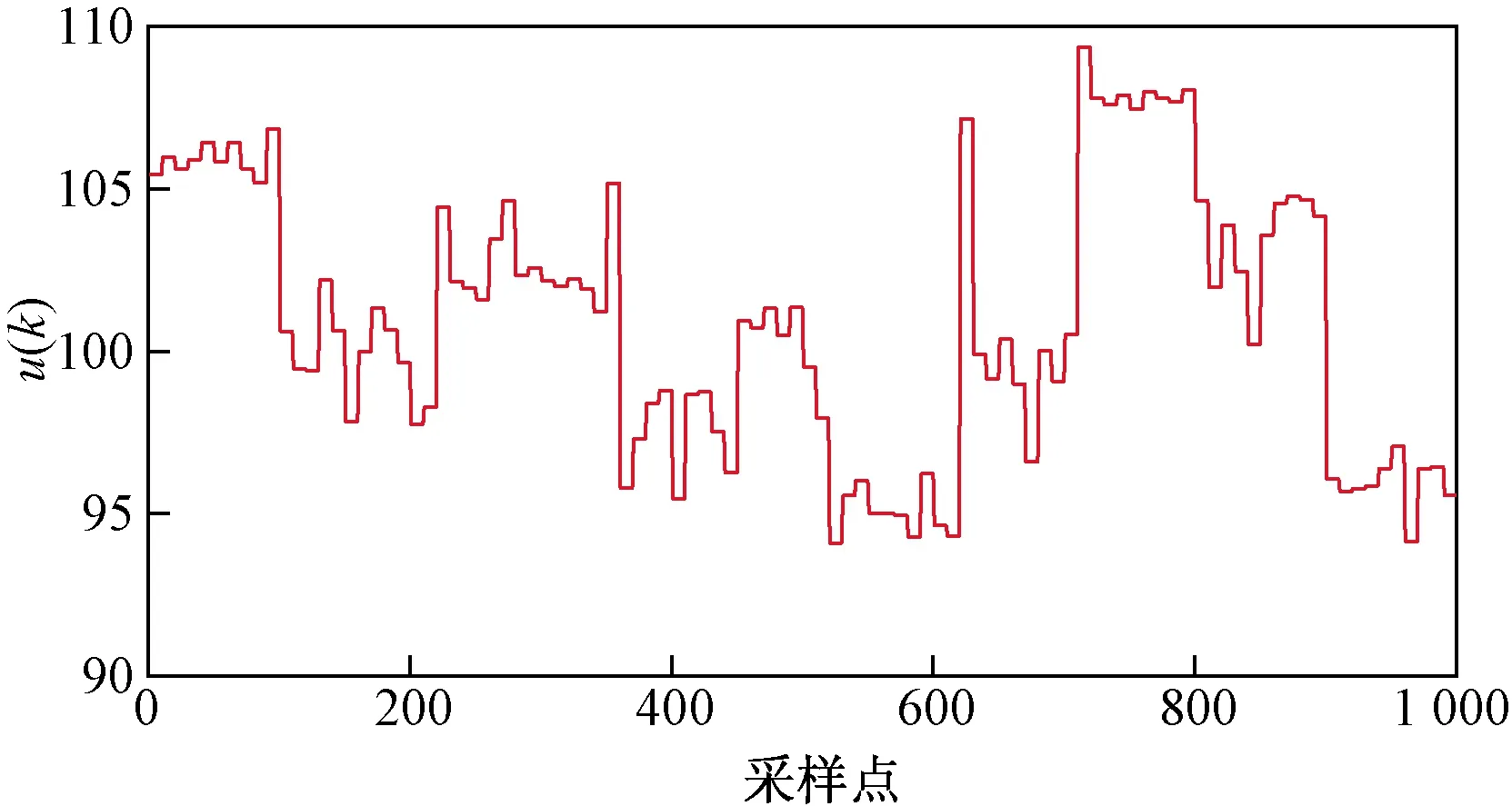
图4 用于采集数据集的控制信号Fig.4 The control signals used to collect data sets

辨识过程中,将模糊规则设置为c=5,模糊度常数设置为η=0.1,遗传操作中最大迭代次数为500,根据采样得到的1 000组数据进行辨识。

图5所示为采用HGA-IFPFCM算法以及HGA算法对CSTR反应过程的辨识曲线,并与实际反应产生的输出信号曲线进行了对比。图6所示为两种辨识算法在遗传操作中随迭代次数产生的均方误差曲线。从图6中可以看出，HGA-IFPFCM算法的进化效果优于HGA算法,具有更快的响应速度和辨识性能。

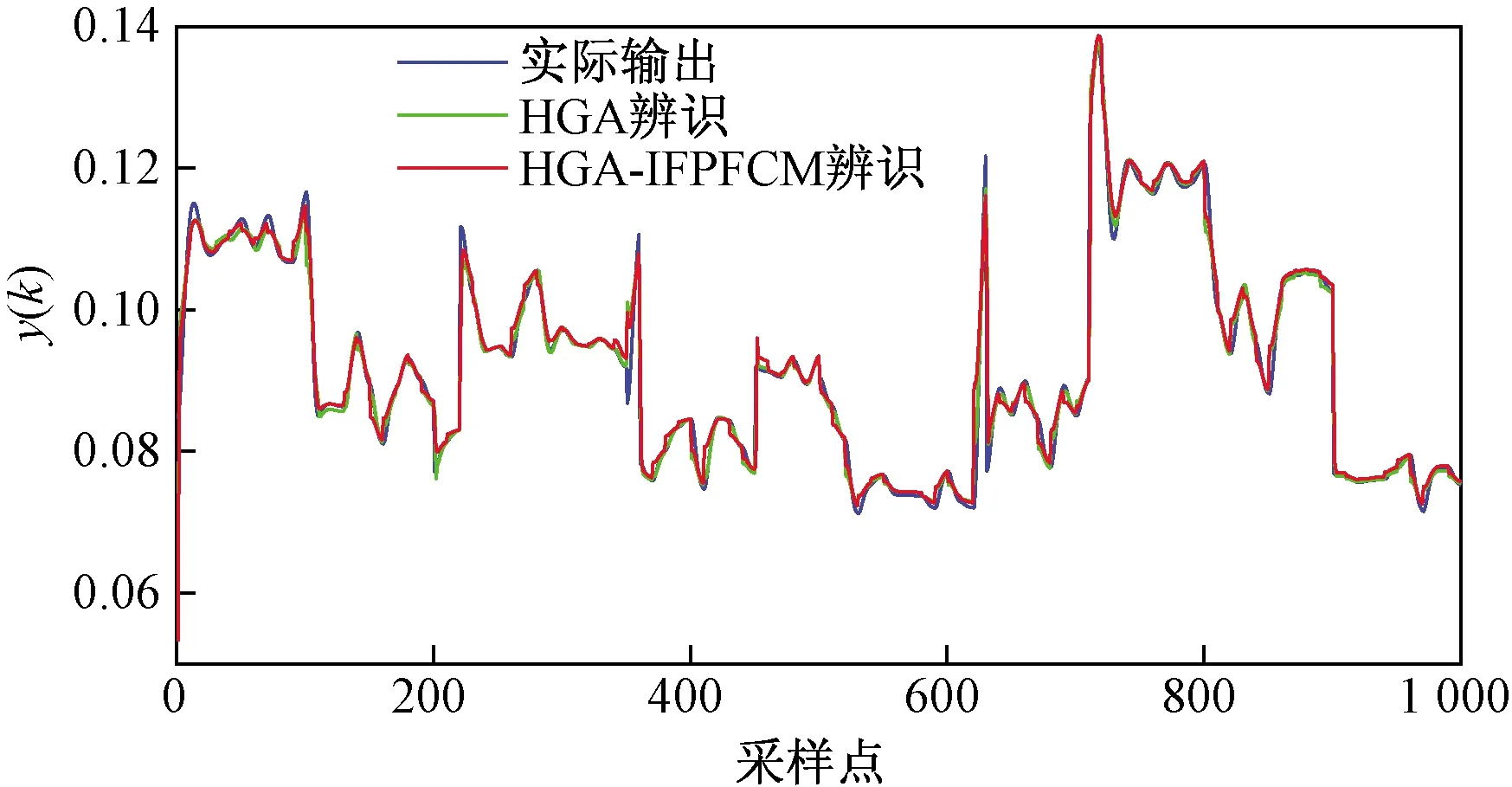
图5 CSTR系统的辨识与实际输出曲线Fig.5 CSTR system identification and actual output curve

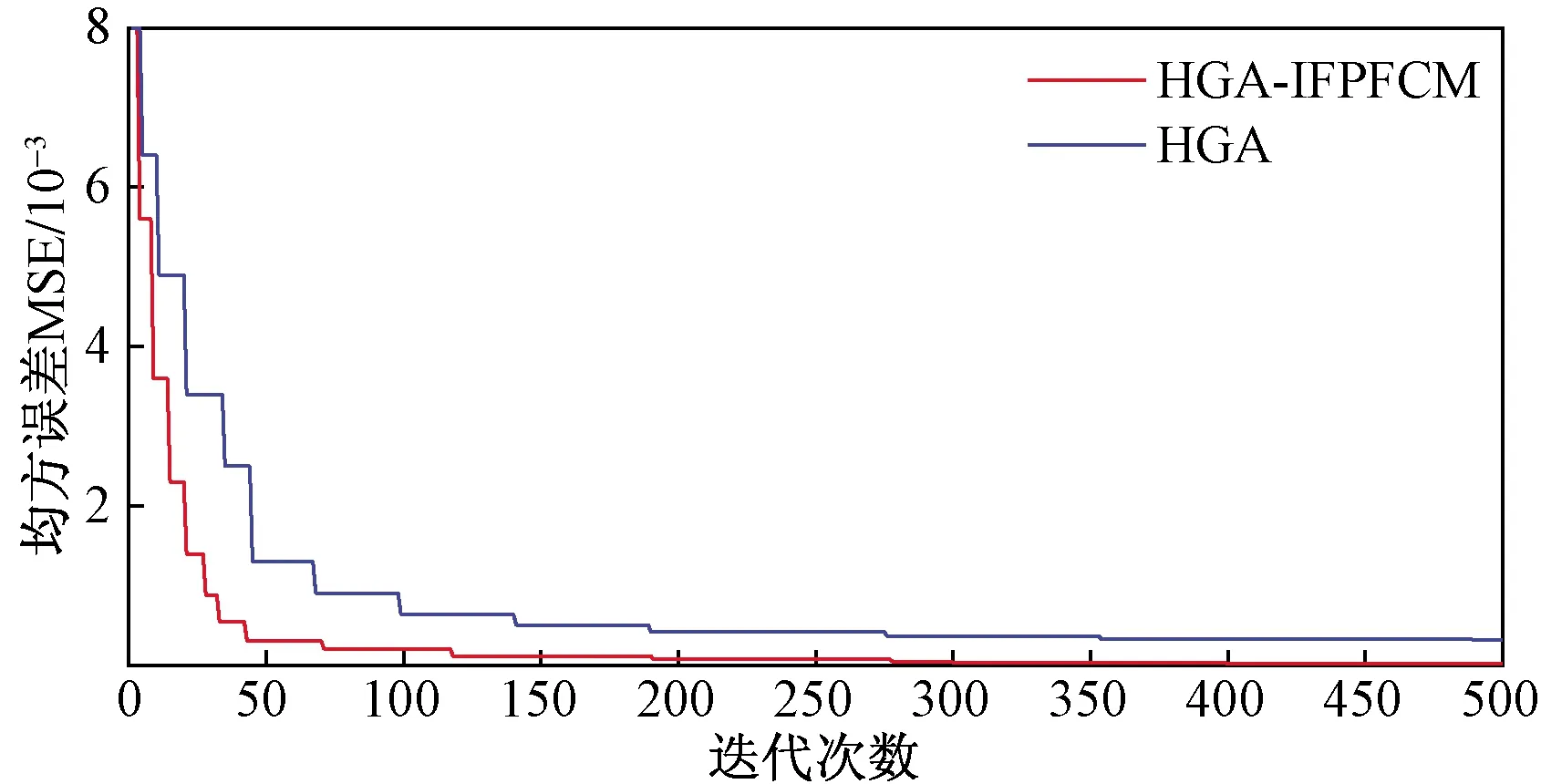
图6 辨识算法随迭代次数产生的均方误差曲线Fig.6 Mean square error curve of identification algorithm with iteration times

为体现本文辨识算法的有效性,在均方误差曲线对比的基础上,对HGA算法和HGA-IFPFCM算法进行辨识算法的误差对比,主要包括均方根误差RMSE以及平均绝对误差MAE,如表2所示。

表2 辨识算法性能对比Table 2 Performance comparison of identification algorithm

从图6以及表2中均可以看出相对于HGA算法,HGA-IFPFCM算法在对CSTR系统进行辨识时的误差较小,性能更好。

分别将浓度以及流量变量CA(t-2)、CA(t-4)、qc(t-1)、qc(t-3)作为CSTR系统T-S模糊模型的输入变量；同时,将CA(t)作为输出变量。通过辨识,CSTR系统T-S模糊模型中输入变量的隶属度函数曲线如图7和图8所示。

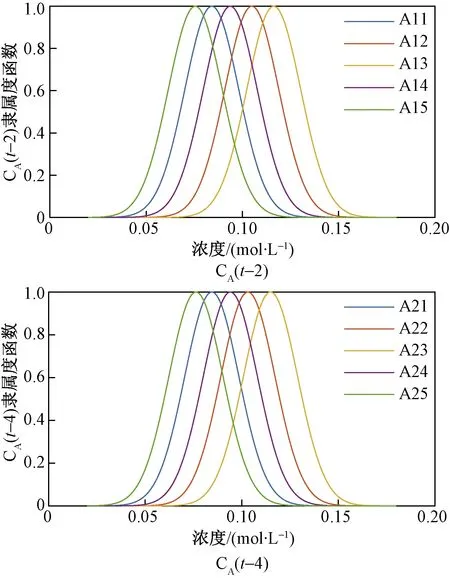
图7 CA(t-2)、CA(t-4)的隶属度函数曲线Fig.7 Membership function curve of CA(t-2)、CA(t-4)

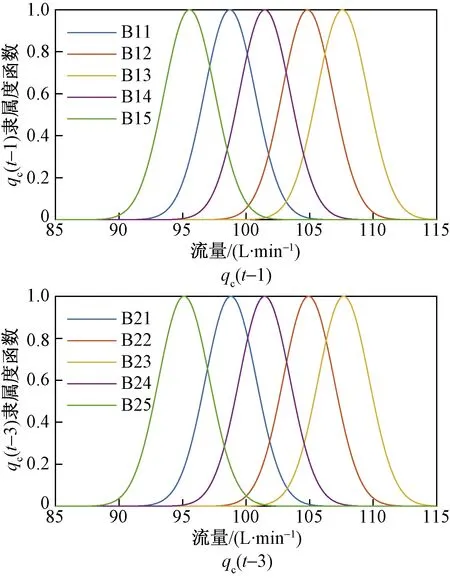
图8 qc(t-1)、qc(t-3)的隶属度函数曲线Fig.8 Membership function curve of qc(t-1)、qc(t-3)

结合1.3节自适应机制遗忘因子递推最小二乘法,通过式(17)实现遗忘因子的参数自适应,进而通过式(15)实现T-S模糊模型后件参数的估计。通过相应的辨识算法,可得到T-S模糊模型的5条规则如式(42)所示。

R1:IFCA(t-2) isA11andCA(t-4) isA21and

qc(t-1) isB11andqc(t-3) isB21

THENCA(t)=-0.015 6CA(t-2)+

1.091 7CA(t-4)-4.549 9×

10-4qc(t-1)-0.003 1qc(t-3)

R2:IFCA(t-2) isA12andCA(t-4) isA22and

qc(t-1) isB12andqc(t-3) isB22

THENCA(t)=-0.036 1CA(t-2)+

0.840 7CA(t-4)-0.001 4qc×

(t-1)-0.019 0qc(t-3)

R3:IFCA(t-2) isA13andCA(t-4) isA23and

qc(t-1) isB13andqc(t-3) isB23

THENCA(t)=-0.062 0CA(t-2)+

0.970 5CA(t-4)-7.562 7×

10-4qc(t-1)-0.012 5qc(t-3)

R4:IFCA(t-2) isA14andCA(t-4) isA24and

qc(t-1) isB14andqc(t-3) isB24

THENCA(t)=-0.014 3CA(t-2)+0.913 4×

CA(t-4)-7.030 3×10-4qc×

(t-1)+0.002 5qc(t-3)

R5:IFCA(t-2) isA15andCA(t-4) isA25and

qc(t-1) isB15andqc(t-3) isB25

THENCA(t)=-0.053 9CA(t-2)+0.781 4×

CA(t-4)-0.002 2qc(t-1)+

0.015 1qc(t-3) (42)

3.3 CSTR系统的AFGPC仿真

基于得到的CSTR系统的T-S模糊模型,结合第2节的AFGPC算法对CSTR进行控制。设定控制参数:控制步长Nu=1、预测步长Np=150、加权系数λ=0.05以及辨识参数:ρ=0.99、φi=1、τi=vi=1×10-9,其中1≤i≤c。此外,与传统PID算法进行控制效果的对比以验证AFGPC算法的性能。其中,PID算法的参数分别设定为Kp=0.4、Ti=0.53、Td=0.2。

按照式(43)设定系统的参考输出值:

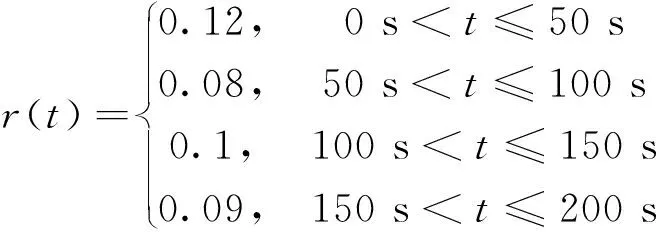
图9所示为在无干扰存在的情况下,PID控制与AFGPC控制效果的对比曲线。从图9中可以看出，在进行曲线跟踪时,AFGPC算法能够更好地逼近期望输出曲线。

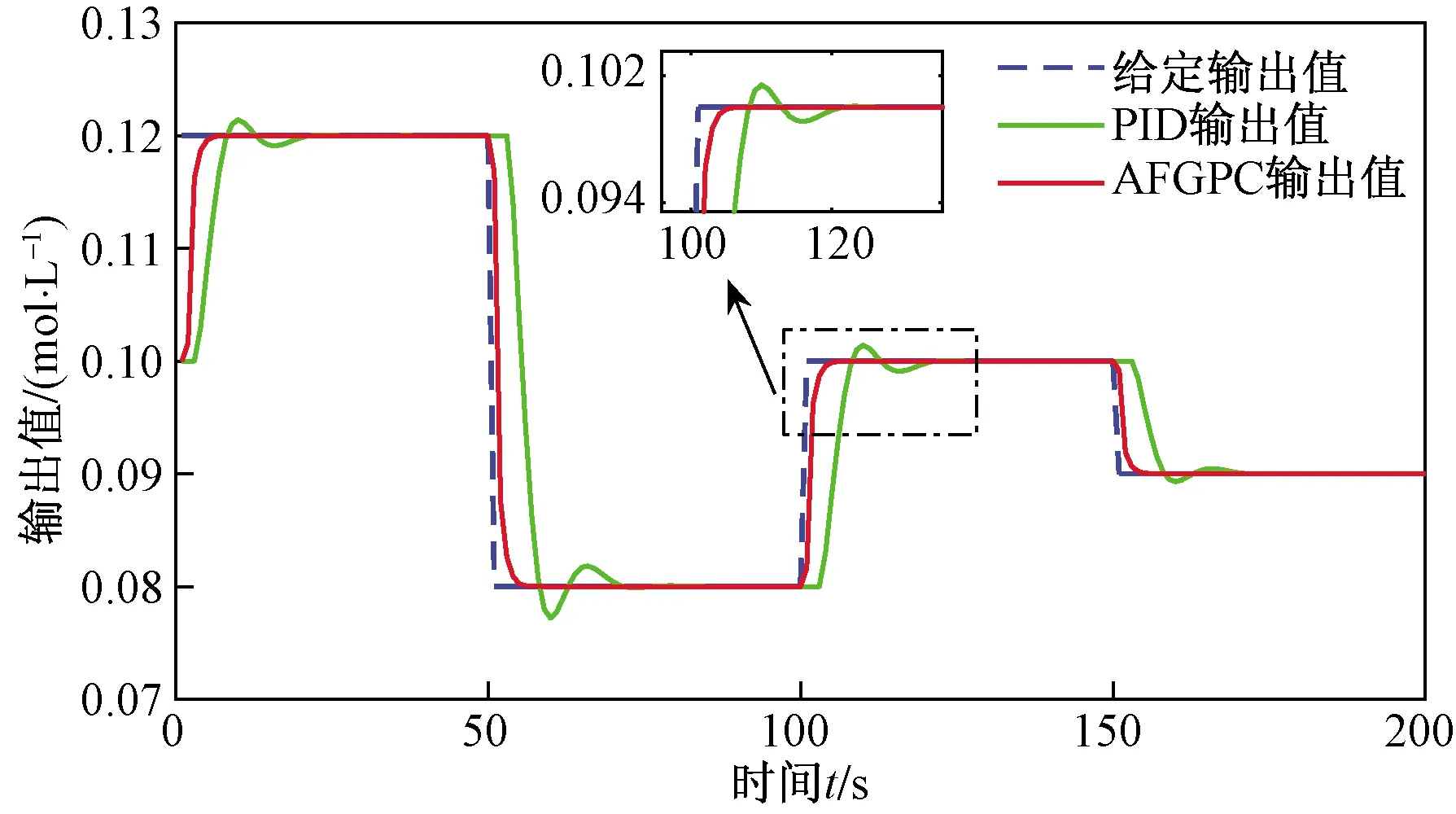
图9 PID与AFGPC控制效果图(无干扰)Fig.9 Control effect diagram of PID and AFGPC(no interference)

通过计算,将PID算法和AFGPC算法所产生的均方根误差RMSE以及平均绝对误差MAE统计如表3所示。

表3 控制算法性能对比(无干扰)Table 3 Performance comparison of control algorithm(no interference)

从表3可以看出,在无干扰的情况下,AFGPC算法的误差指标相对较小。

为验证控制器的抗干扰性能,分别在125 s、175 s时增加扰动信号。图10所示为PID控制与AFGPC的控制效果对比曲线。从图10中可以看出,相较于PID控制,AFGPC算法能够更快速地修正误差,消除干扰。

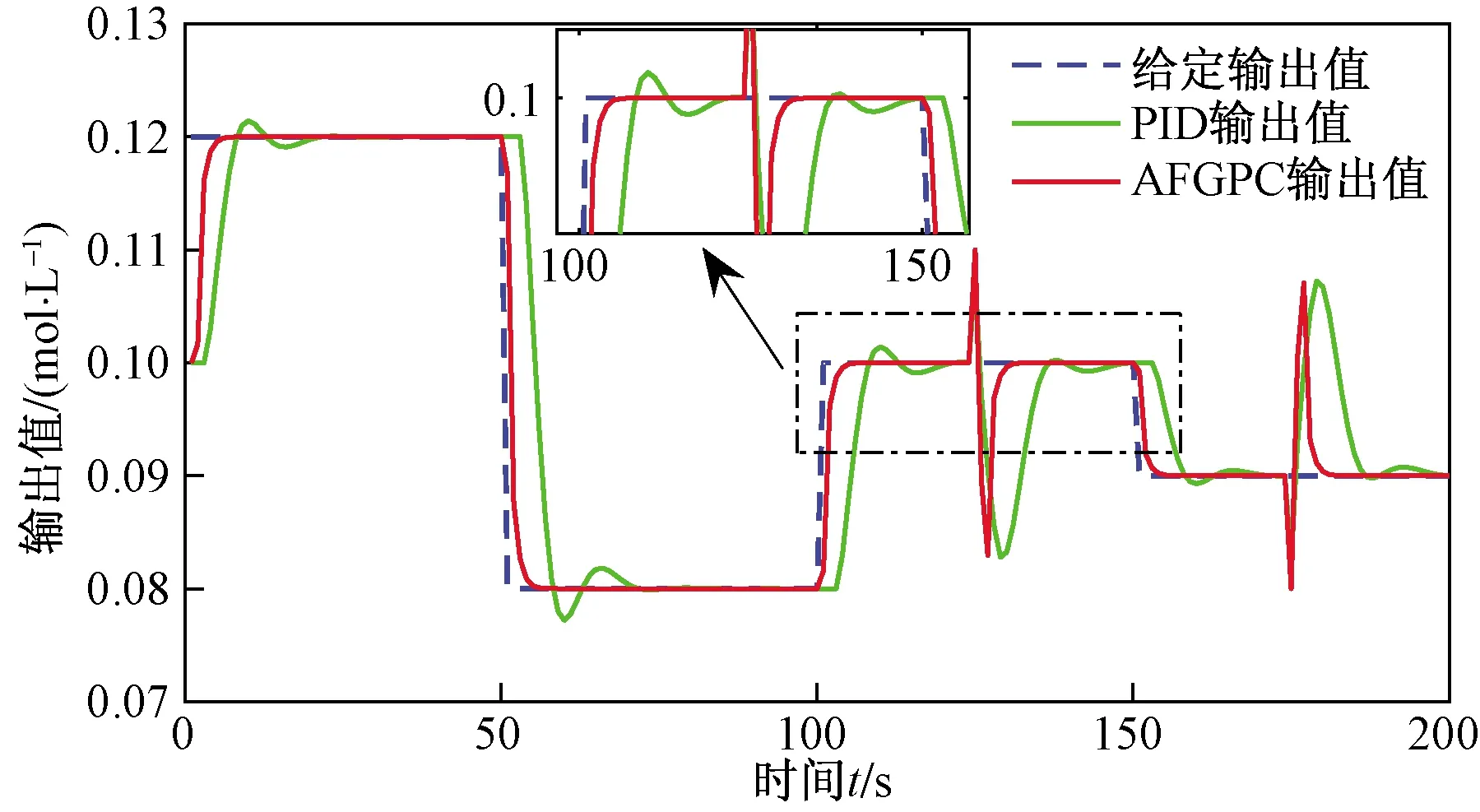
图10 PID与AFGPC控制效果图(有干扰)Fig.10 Control effect diagram of PID and AFGPC (with interference)

与无干扰的情况相对应,将有干扰存在时的PID算法和 AFGPC 算法所产生的均方根误差RMSE以及平均绝对误差MAE统计如表4所示。

表4 控制算法性能对比(有干扰)Table 4 Performance comparison of control algorithm(with interference)

从表4可以看出,在有干扰存在的情况下,AFGPC算法的误差指标仍相对较小。因此,在工业环境较为复杂的情况下,采用AFGPC算法能够更好地实现对CSTR的控制。

4 结论

选取化工领域常见的CSTR作为研究对象,根据实际工业现场采集到的数据集,分别采用HGA算法和HGA-IFPFCM算法对T-S模糊模型的前件结构参数进行辨识。根据辨识结果,与传统HGA算法相比,HGA-IFPFCM算法的建模性能较好且辨识精度较高,将该算法与自适应机制遗忘因子递推最小二乘法相结合进行后件参数的估计与优化,得到CSTR的T-S模糊模型。最后,通过PID算法和AFGPC 算法对CSTR系统进行控制,同时对存在干扰的情况也进行了比较。仿真结果表明,在对CSTR系统进行控制时,相对于PID算法,AFGPC算法具有更好的控制性能和抗干扰性能。