基于动态模糊推理的舒适温度在线预测

白 燕,冯壮壮,张 玮

(1.西安建筑科技大学 理学院， 西安 710055;2.西安建筑科技大学 信息与控制工程学院，西安 710055)

0 引言

舒适的室内环境是人们健康生活和高效工作的前提，随着智能建筑的迅速发展，通过楼宇自控系统对建筑设备实行有效的控制和管理，为营造舒适的室内热环境提供有利条件。自Fanger提出PMV(predicted mean vote)热舒适评价指标以来，热舒适在环境热舒适度评价、室内热环境控制以及空调系统节能优化等领域得到广泛研究。但热舒适不仅受当地气候、生活习惯、风俗、热经历、热期望、热环境响应及个人体质等多因素的影响，也具有随着活动状况、衣着、饮食、情绪的不同而变化的动态变化性(时变特征)[1]。这种热舒适动态差异性造成个体间的舒适偏好温度偏差在2.6以上[2]，使得基于PMV指标温度设定点的热环境控制只能在统计意义上满足大多数人的舒适性，难以满足某一个体或群体热舒适多样性的需求，从而造成能源浪费[3]。

近年来，基于热感觉的热环境控制为有效解决室内环境与用户舒适度不匹配问题提供了新的途径，已在国内外进行了大量研究，并在预测准确性和节能方面取得了良好的效果。Kim等人基于大量热舒适性研究的重要概念和方法，为个人舒适模型开发了一个统一的框架[4]。在个性化热舒适模型的构建中，已有研究采用了支持向量机、隐马尔可夫模型学习算法、贝叶斯分类推理算法等机器学习算法；并对个人热偏好进行了预测，相对传统PMV和热适应模型的预测结果，其预测准确率提高了20%～40%[5]。李慧等学者提出用户热舒适区模糊学习算法实现了不同用户的热舒适区在线学习，并应用到周期性交替变化的动态热舒适控制策略中，使系统节能28.7%[4]。Erickson和Cerpa基于参与式感知思想将人引入环境控制回路以避免过于繁琐的热舒适度测量，通过热感觉实时反馈，准确连续地调节温度，提高用户舒适度同时，系统实现了10.1%的节能[6]。

上述研究中多数算法在建模过程中用户热感觉反馈信息的获取方式以自主开发的硬件交互设备媒介或以问卷、调查走访形式收集用户热舒适评价投票，两种交互方案的程序不仅繁杂，而且数据采集时间受限，用户体验效果差。而智能手机的普及为数据采集带来了极大地便利，降低了对用户干扰。同时针对热舒适时变性问题，多数研究在采用信息数据驱动技术作为解决方案的同时，利用更新后的学习样本重新学习，但随着样本量递增不仅增大了计算负荷，也无法体现出新样本对热舒适的影响趋势。依据王福林、江亿等学者对于用户热舒适实时预测及热感觉控制过程中参数简化的研究，仅采用温湿度作为预测和调控参数能够满足用户个性化热舒适的环境控制需求[7-8]。因此热感觉信息便捷获取和参数简化的热舒适动态预测仍需进一步研究。

本文融合了用户投票评价方法和在线学习方法，开发出移动端智能交互系统对用户热舒适感数据进行采集；在此基础上，以空气温度与热感觉少量指标为学习样本简化热舒适在线预测模型，设计动态神经模糊推理算法，使得仅以新样本点更新用户热偏好模糊规则和迭代模型输出系数完成原始学习模型增量学习以预测用户偏好温度，无需对更新后样本重新学习，大大降低计算复杂度。在仿真分析的基础上，将算法应用于现场实验数据、ASHRAE(美国采暖、制冷与空调工程师学会)数据集以验证用户舒适温度学习效果。有效表明该预测模型可用于智能空调系统中，为合理设定空调温度提供了实际应用价值。

1 智能交互系统设计及学习样本构建

移动交互终端以其低投资、易维护、交互便捷和信息可视化等优势被热舒适、无人机控制、医学诊断等研究领域广泛采用。本文基于Linux平台，采用物联网技术，在Eclipse软件环境下设计并开发移动端智能交互系统，系统示意图如图1所示。该系统采集用户热舒适感数据为用户热舒适在线预测模型研究提供学习样本。热舒适感数据由用户基本信息、热环境参数和热投票参数组成，分别包括年龄、性别、活动状态、衣服热阻等信息，空气温度、空气流速、相对湿度信息，热感觉，热偏好，热可接受性等信息，具体参数如表1所示。

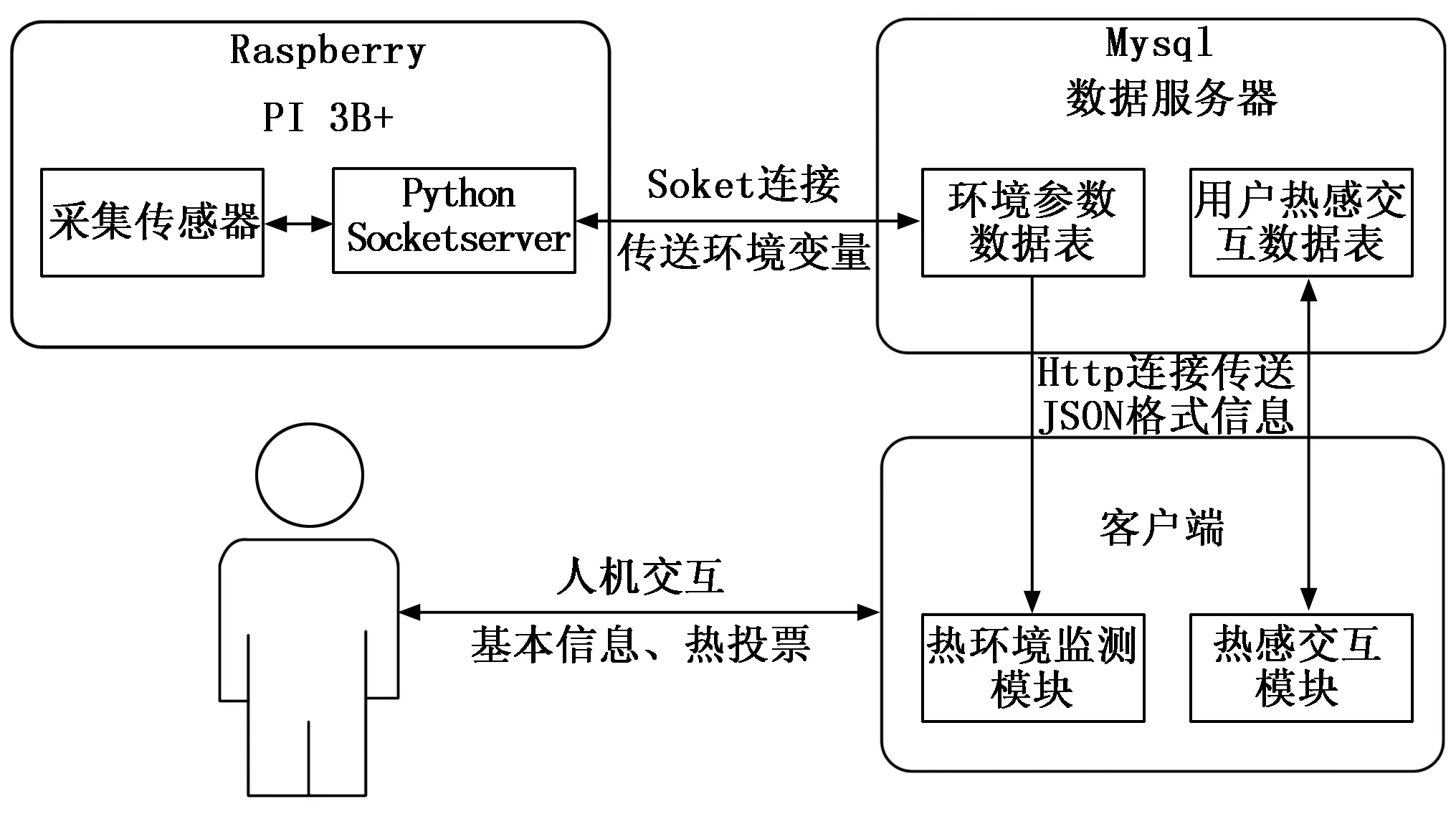
图1 智能交互系统示意图

表1 热舒适感数据类型表

智能交互系统主要包括热感交互及热环境监测两大模块。热感交互模块以手机移动端APP为用户接口，通过热感交互页面将用户基本信息和热投票等信息以时间序列形式存储于后台数据库。热环境监测模块由Raspberry Pi 3B+环境采集器集成各类传感器，实现温度、湿度、风速等环境信息的采集，以时间序列形式存储于后台数据库；手机移动客户端APP以用户请求为触发条件将数据库中的检测参数实时更新至环境监测页面。系统前台基于Visual Studio Code平台，采用Html5、Javascript脚本语言完成页面开发，移动客户端和数据采集系统分别采用Http协议及Socket套接字与后台服务器建立连接，将环境参数与用户交互参数分别存储于后台数据库中的“环境参数数据表”及“用户热感交互数据表”，并以Json格式完成数据传输。

移动客户端交互界面如图2所示，交互信息包括年龄、性别、活动状态、着装等用户基本信息和热可接受性、热偏好、热感觉指标(TPI，thermal perception index)等热投票参数。其中，TPI定义为实时反馈的用户真实热感觉，参考ASHRAE标准热舒适七点标度尺，取[-3,+3]的范围；并根据ASHRAE标准中以PMV在-0.5～0.5作为舒适范围，PMV在0点作为最佳舒适点的推荐准则，本文将TPI以-0.5～0.5的取值范围作为用户个人的热舒适区，以TPI为0定义用户的最佳舒适点。同时以滑动条的形式实现交互，正值代表热感，负值代表冷感，绝对值越大表明用户热感觉越明显[9]；学习样本以热舒适感数据集中用户的TPI和空气温度(T)进行定义，其它参数用于用户热感觉信息检验以进行学习样本的清洗。

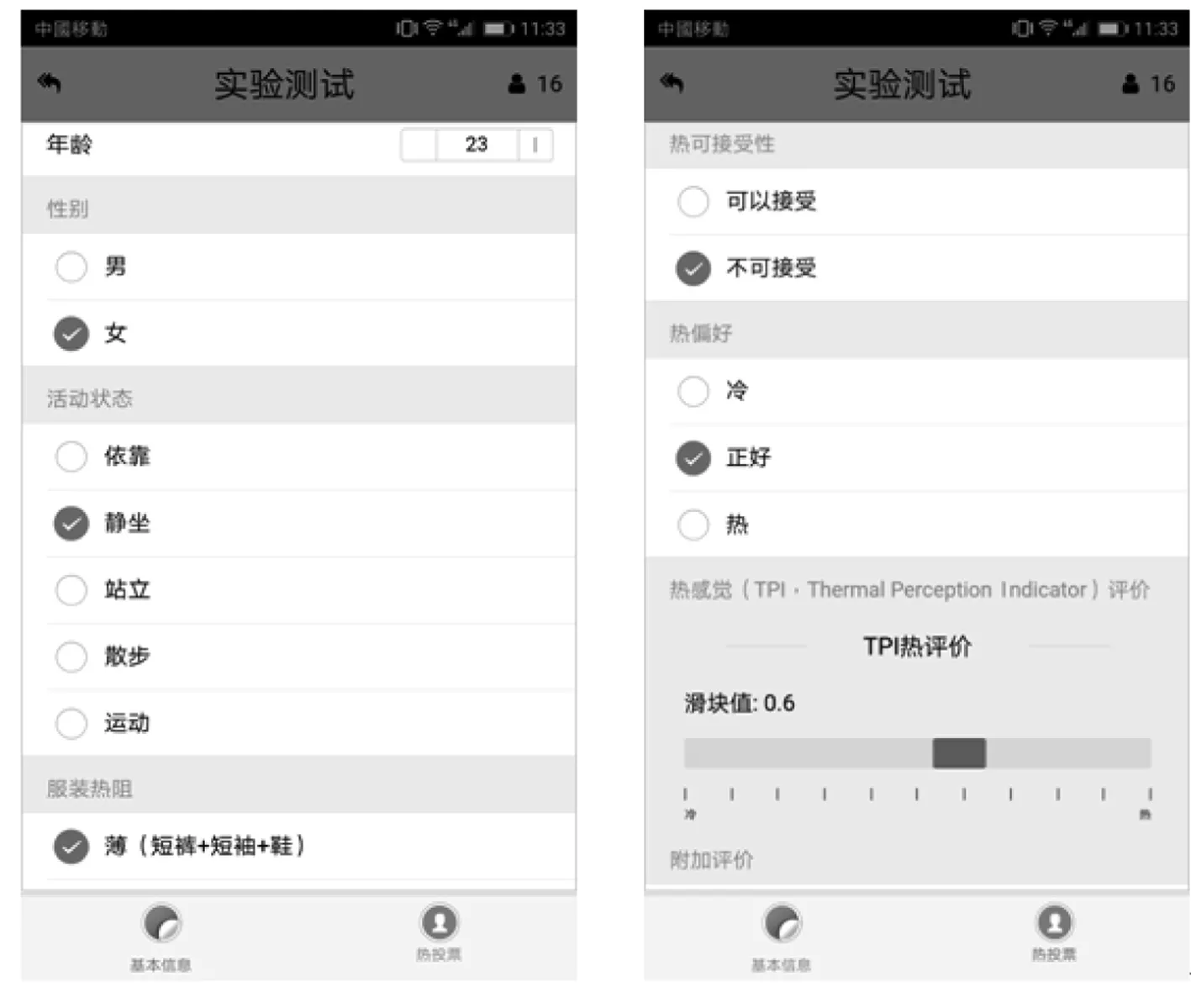
图2 用户交互界面

2 用户热舒适在线预测模型

动态进化神经模糊推理系统(dynamic evolving neuro-fuzzy inference system，DENFIS)以其单变量建模、预测精度高、可靠性强、快速学习等特性适用于动态系统的理论及应用研究[10-11]，因此它是模拟具有时变特性的用户热舒适在线学习过程的最佳模型。由于室内空气温度对带有主观模糊性的热感觉有着正相关关系，为合理确定用户舒适区间，以用户舒适温度范围对用户热舒适区简化研究[12]。将进化聚类算法(evolving clustering method, ECM)与模糊隶属度函数相结合，通过在线聚类方式构建模糊集，提取模糊规则，确定模糊规则前件；并采用Takagi-Sugeno推理模型，依据局域线性模糊推理输出，构建模糊规则后件。

2.1 增量聚类方法ECM

ECM是一种动态的、在线的、受某一最大距离Dthr约束的聚类算法，随输入样本量的增加动态增加聚类个数或变更聚类中心和聚类半径。聚类过程从一个空的聚类集合开始，随着新样本数据的增加，动态地增加聚类数或更新聚类中心及聚类半径，当半径达到阈值Dthr时停止更新。将清洗后学习样本进行聚类，算法步骤如下。

步骤1:创建第一个类C1，将第一个输入样本X1(TPI1,T1)，作为该类的聚类中心Cc1，初始化聚类半径Ru1=0。

步骤2:如果所有样本数据处理完毕，则聚类完成；否则，利用公式(1)计算当前输入样本Xi(TPIi,Ti)，i=1,2,3…,p，与聚类中心Ccj,j=1,2,3…,q,的欧式距离Dij，其中样本数据为2维向量，因此z=1，2。

(1)

步骤3:如果存在一个Dij，满足Dij≤Ruj,则表明样本Xi属于已有的第m个聚类Cm，即Dim≤Rum，此时聚类无需更新，返回步骤2；否则，执行步骤4。

步骤4:如果计算样本Xi与所有聚类中心距离均大于聚类半径Ruj，则计算Sij=Dij+Ruj,并取最小值min(Sij)，寻找出类Ca使得Sia=min(Sij)。

步骤5:如果Sia>2×Dthr，则样本Xi不属于当前已有的类，返回步骤1；否则，执行步骤6。

步骤6:如果Sia≤2×Dthr，更新类Ca的聚类中心Cca和聚类半径Ruj=Sia/2，返回步骤2。

通过ECM算法，不同用户的样本点都能在有限数量的聚类集合得到不同聚类，且随着用户的交互，样本量逐渐增加，聚类产生的聚类集合也动态变化。

2.2 提取模糊规则

利用ECM聚类算法确定学习样本空间的聚类集合，进一步建立模糊集合，构建模糊规则。DENFIS系统有n条推理规则，表述如下：

IfTPIiisR1，Theny1isf1(TPI)

IfTPIiisR2，Theny2isf2(TPI)

⋮

IfTPIiisRn，Thenynisfn(TPI)

这里TPIi，i=1,2,3…,p为第i个学习样本Xi(TPIi,Ti)中的TPI；Rk，k=1,2,3,…,n,为不同的模糊集，通过聚类集合确定，并由其对应的三角型模糊隶属度函数μ定义，如式(2)。

μ(TPIi)=nF(TPIi,a,b,c)=

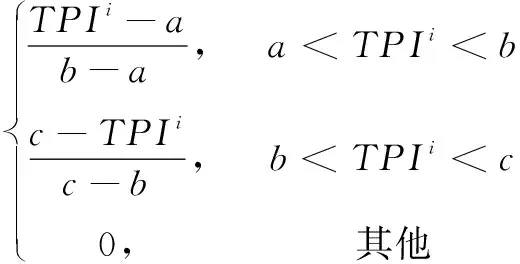
(2)

式中，b为输入空间的聚类中心，a=b-d×Dthr，c=b+d×Dthr，d=1.2～2。

在推理后件部分，yk以温度作为每条规则的输出结果，采用一阶线性函数fk，k=1,2,3,…,n，如式(3)。利用以上模糊规则，每输入一个TPIi，系统推理结果为每条模糊规则输出的加权平均值：

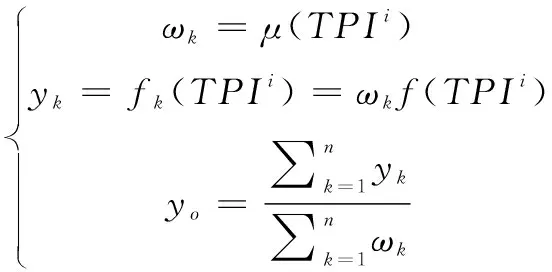
(3)

式中，yo为系统推理结果；ωk是每个隶属度规则的权重，等于输入TPIi所对应的函数隶属度。

2.3 规则输出函数

推理系统模糊规则后件输出函数采用一阶Takagi-Sugeno模型，即：

y=f(TPI)=β0+β1×TPI

(4)

式中，系数β0和β1是通过线性最小二乘估计法(least squares estimate，LSE)针对p组学习数据Xi(TPIi,Ti)，i=1,2,3…,p产生和修正，如式(5)。

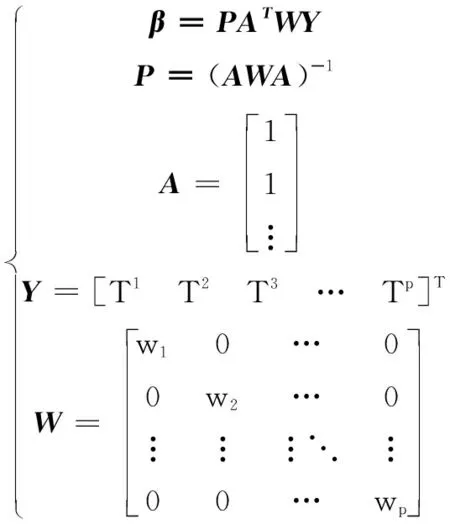
(5)

式中，β=[β0β1]T，为系数矩阵；A为用户TPI输入矩阵；Y为学习样本中温度的输出矩阵；W对角线wi为第i个样本点到该样本点所属的聚类中心之间的距离。

2.4 模型增量学习

系统有样本数据输入时，该模型通过两种方式完成在线学习，一种是依据模糊规则校正的观点[13]，以ECM增量计算新样本点修正已有的聚类集合，更改样本的模糊规则；另一种是依据参数在线整定的思想[14]，采用带遗忘因子的加权递归最小二乘法对输出函数系数β进行迭代计算以保证最新样本数据对模型的权重比，如式(6)所示。

(6)

3 用户热舒适预测及模型检验

3.1 仿真实验研究

由于客观环境、生理及心理等多因素的存在对用户个人热舒适均产生影响，使得无法计算用户个体热舒适准确模型，须进行有效仿真实验刻画用户个体热舒适基准模型。模拟背景为办公建筑环境，该环境下用户行为习惯(着装和活动)存在规律性，即办公环境下个体自身的衣服热阻与新陈代谢率相对固定。因此分别依据青年、中年和老年三类代表性人群的特征，对新陈代谢率、服装热阻、空气流速以及相对湿度等参数进行设定，相关参数如表2所示。

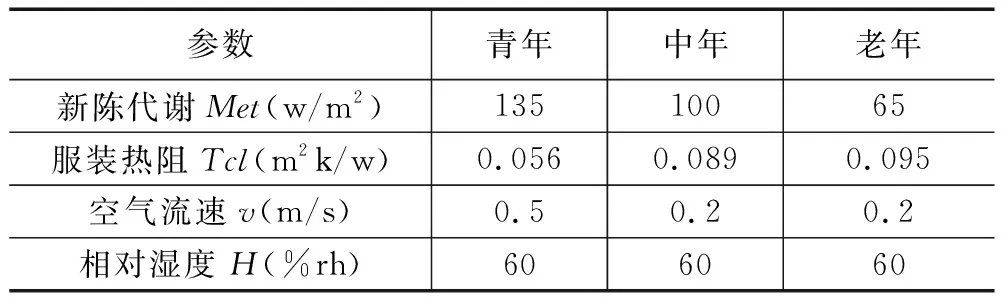
表2 3种类型人群的PMV计算相关参数设置

基于Fanger教授对于室内空气温度与PMV值关系的研究结果，即空气流速、相对湿度、辐射温度、新陈代谢和服装热阻参数相同情况下两者存在线性关系，采用2.3节公式(4)，构建方程T=f(PMV)作为用户基准模型；并考虑现场交互过程中用户反馈信息受到个人情绪、心理状况、环境干扰和感知误差等因素的影响，添加N(0,σ2)随机噪声来模拟现场用户交互数据。根据经验选取方差为2 ℃，分别生成3组典型用户热舒适交互数据以建立学习样本，并通过ECM分别完成样本的聚类，如图3所示。

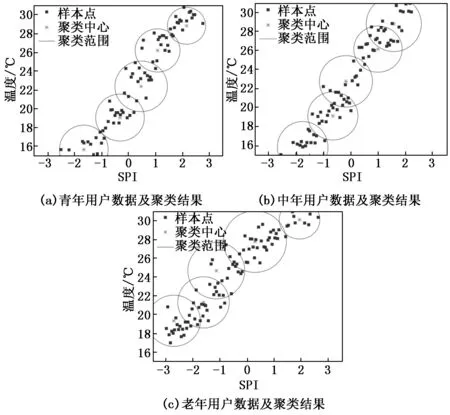
图3 仿真实验用户数据及聚类结果

由图3可以看出，ECM聚类算法都将青年、中年和老年用户样本数据聚成5个聚类集合，但聚类集合空间结构不同，即聚类中心与聚类半径不同，体现了不同用户热舒适的个性化数据模式。依据聚类结果进一步构建模糊集，并使用三角隶属度函数计算三类代表性用户的模糊分区，结果如图4所示。

图4 仿真实验用户模糊分区

图4显示了三名代表性用户自身隶属度函数曲线，也可以看出不同用户热舒适数据具有个性化数据模式的特征。基于上述模糊推理系统前件构建，使用Takagi-Sugeno模型推理输出三类典型用户的热舒适预测结果，如图5所示。

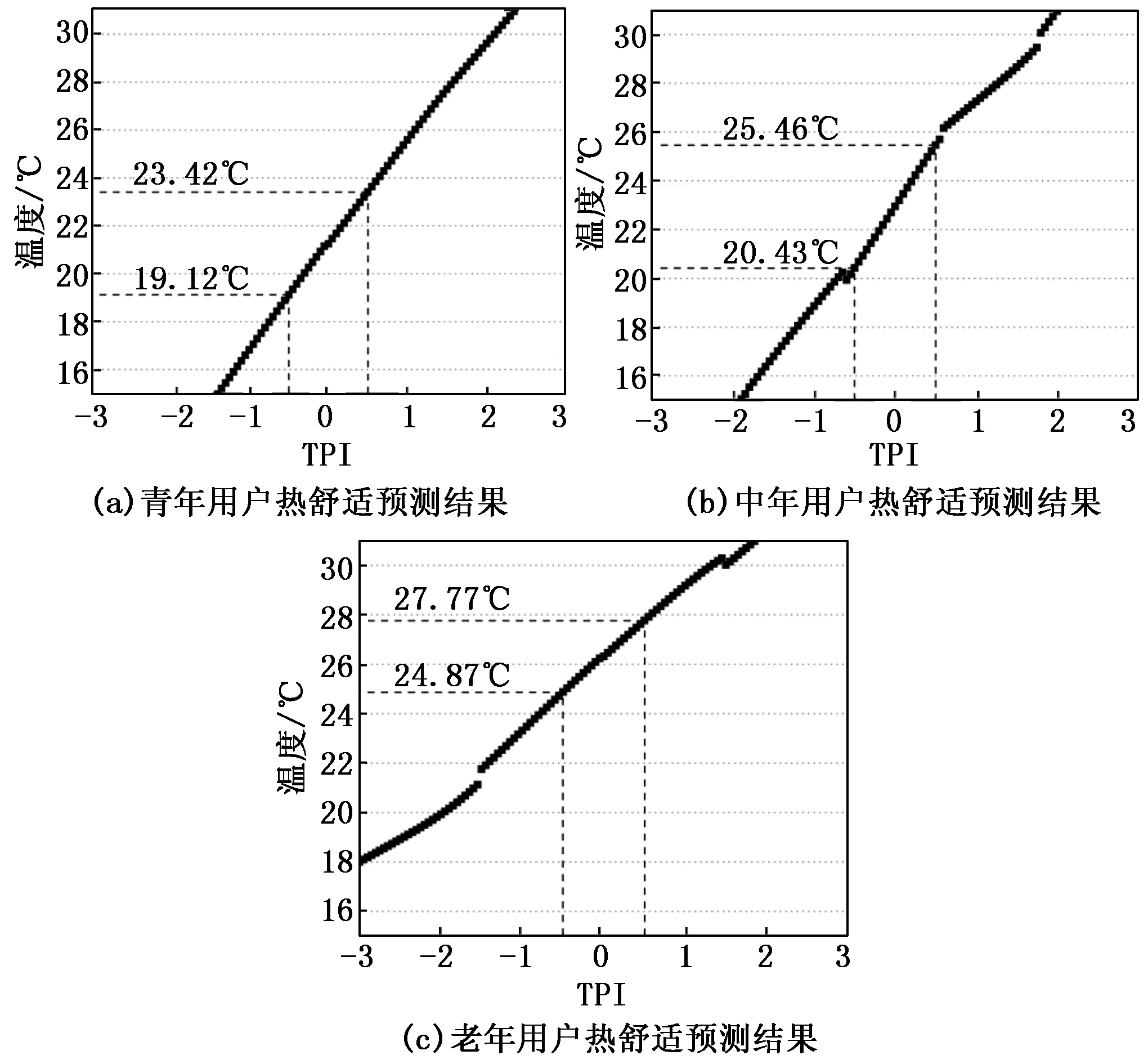
图5 仿真实验用户热舒适预测结果

模糊推理预测结果为青年用户最佳的热舒适温度为21.25 ℃，舒适温度范围为19.12～23.42 ℃；中年用户最佳的热舒适温度为22.99 ℃，舒适温度范围为20.43～25.46 ℃；老年用户最佳的热舒适温度为26.32 ℃，舒适温度范围为24.87～27.77 ℃。从仿真实验结果看出，青年用户与老年用户的舒适温度最大计算温差可达8.65 ℃，证明不同特征用户的个人舒适温度存在较大差异，因此预测用户舒适温度对现有温度设定存在必要性。

为验证热舒适在线预测模型的准确性，使用混淆矩阵对准确率P进行定义，即为所有正确预测的数量除以预测总量所得的比值，如式(7)；混响矩阵如表3所示，其中预测和实际一致则为真，预测和实际不一致则为假，如果预测出来是“正”的，则为“阳”，预测结果为 “负”，则为“阴”。另外通过分析模型预测值与基准模型值及现场样本数据的均方偏差(RMSE)对用户个体热舒适学习效果进行误差分析，如式(8)。

表3 混淆矩阵

(7)

式中,TP*为真阳性，TN*为真阴性，FP*为假阳性，FN*为假阴性。

(8)

式中，yi为第i个样本点或基准模型中TPI对应的温度值；y*i是第i个样本点中TPI对应的模型预测值。

模型预测的误差结果见表4，青年、中年及老年用户的热舒适模型预测值与基准模型RMSE分别为0.247 ℃、0.286 ℃、0.396 ℃。模型预测结果在保证与用户基准模型误差小于0.5 ℃的误差条件下对青年、中年及老年用户舒适温度范围预测准确率分别为90.5%、81.0%、85.7%，远高于传统ASHRAE PMV-PPD标准对个人舒适温度预测的准确性56%[15]。青年、中年和老年用户的热舒适模型预测值与交互样本误差分别为1～1.6 ℃内。其误差原因为用户在对TPI进行反馈时，自身热感觉存在一定的模糊性，主观反馈热舒适具有不确定性。因此，DENFIS算法可以从含交互误差的数据中准确预测用户热舒适，降低交互过程中主观性等干扰因素造成的误差。

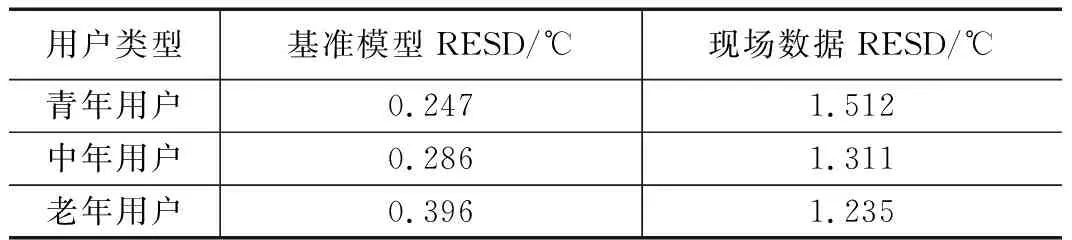
表4 模型预测值与基准模型或现场数据值之间误差

此外，聚类半径阈值Dthr选取可影响聚类集的数量，从而影响模糊集的数量，由图6可以看出，随着Dthr增大，模糊集的数量逐渐减小，且变化率逐步降低。因为聚类半径阈值Dthr的增大，使得聚类集合范围增大可有效覆盖样本点数量，从而模糊集数随Dthr的增大迅速减小，导致其变化率逐步降低。

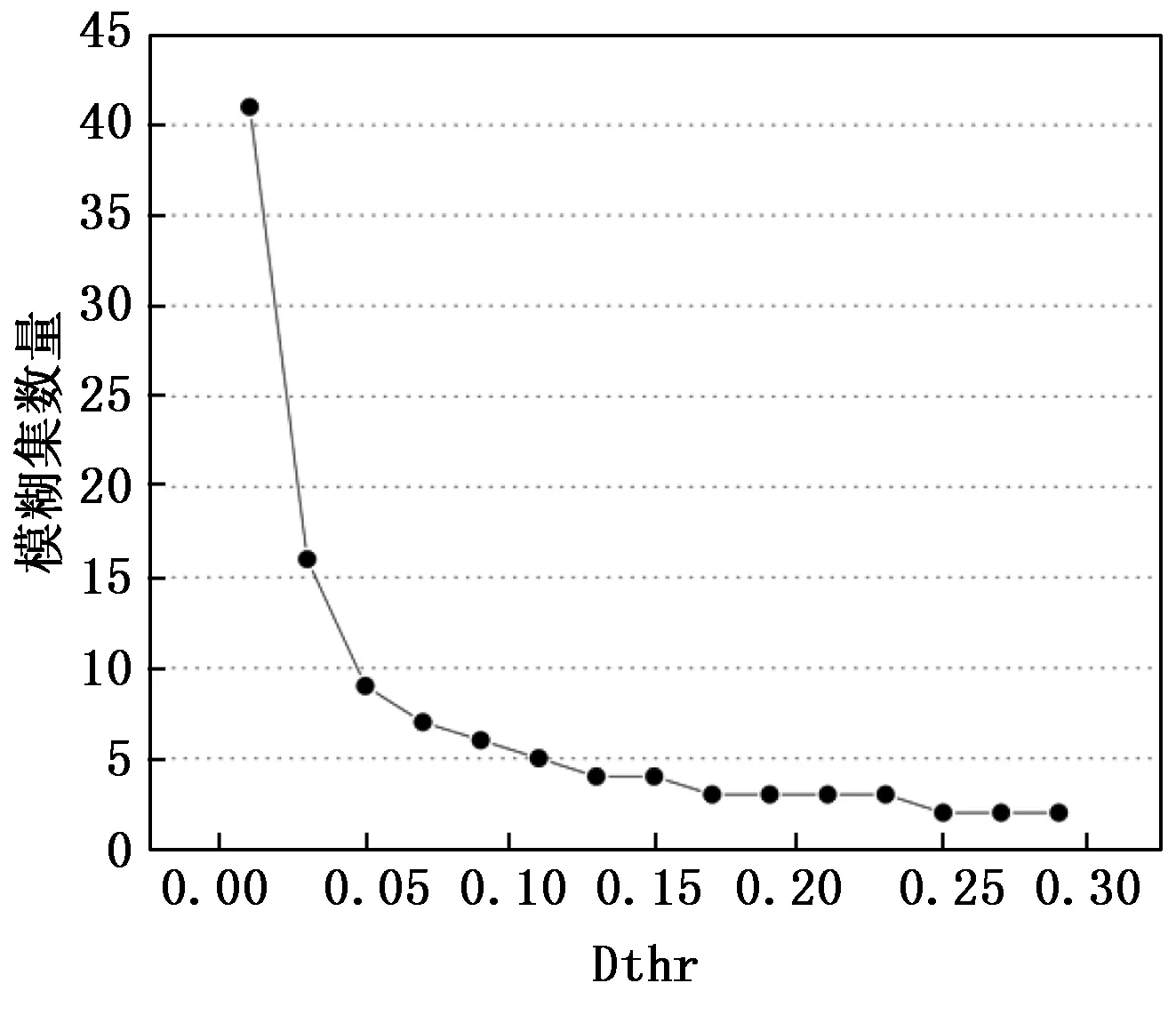
图6 不同Dthr的模糊集数量

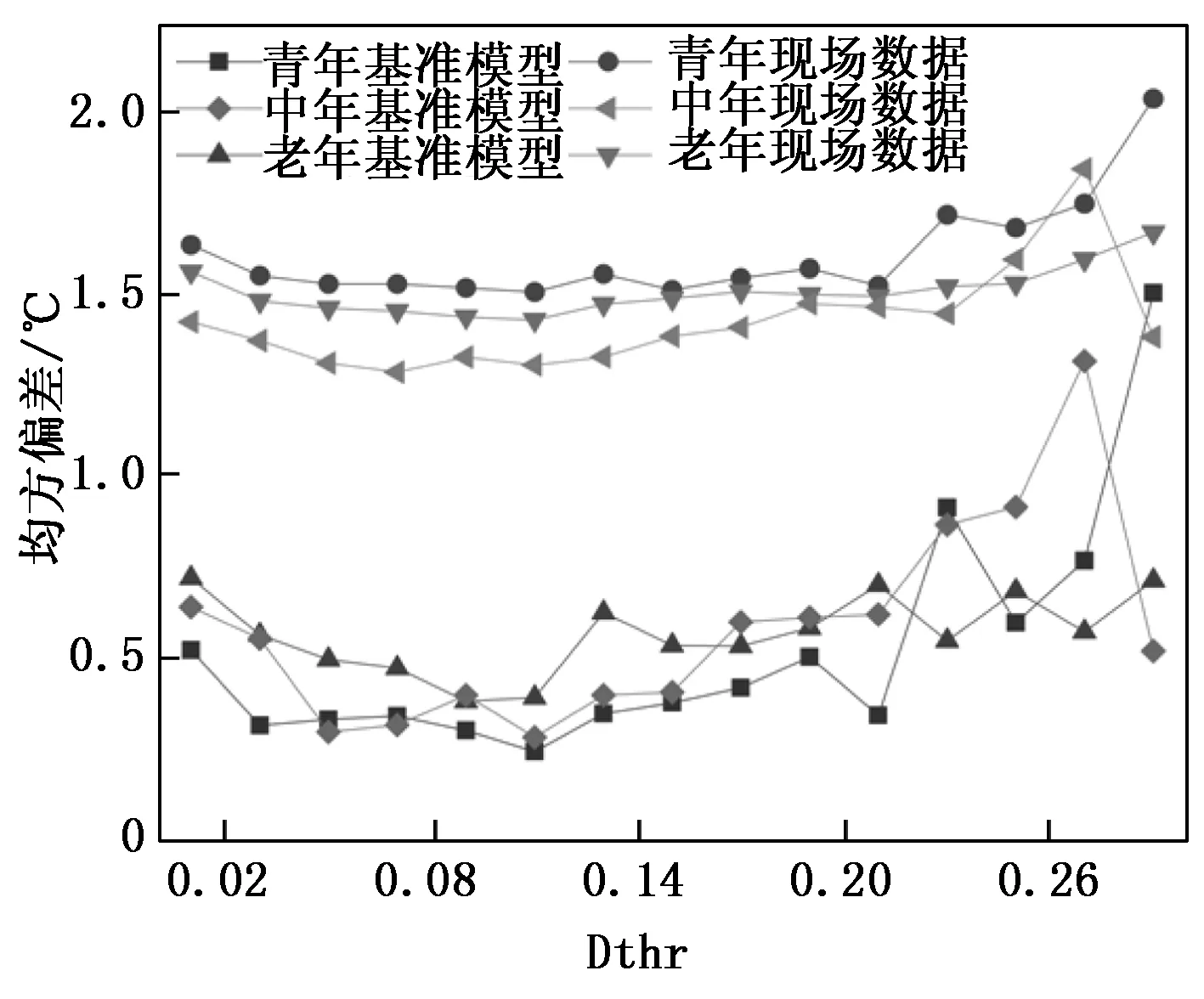
图7 Dthr对模型推理预测误差的影响

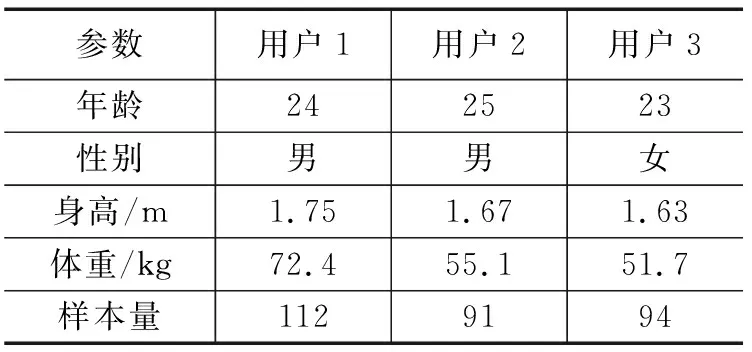
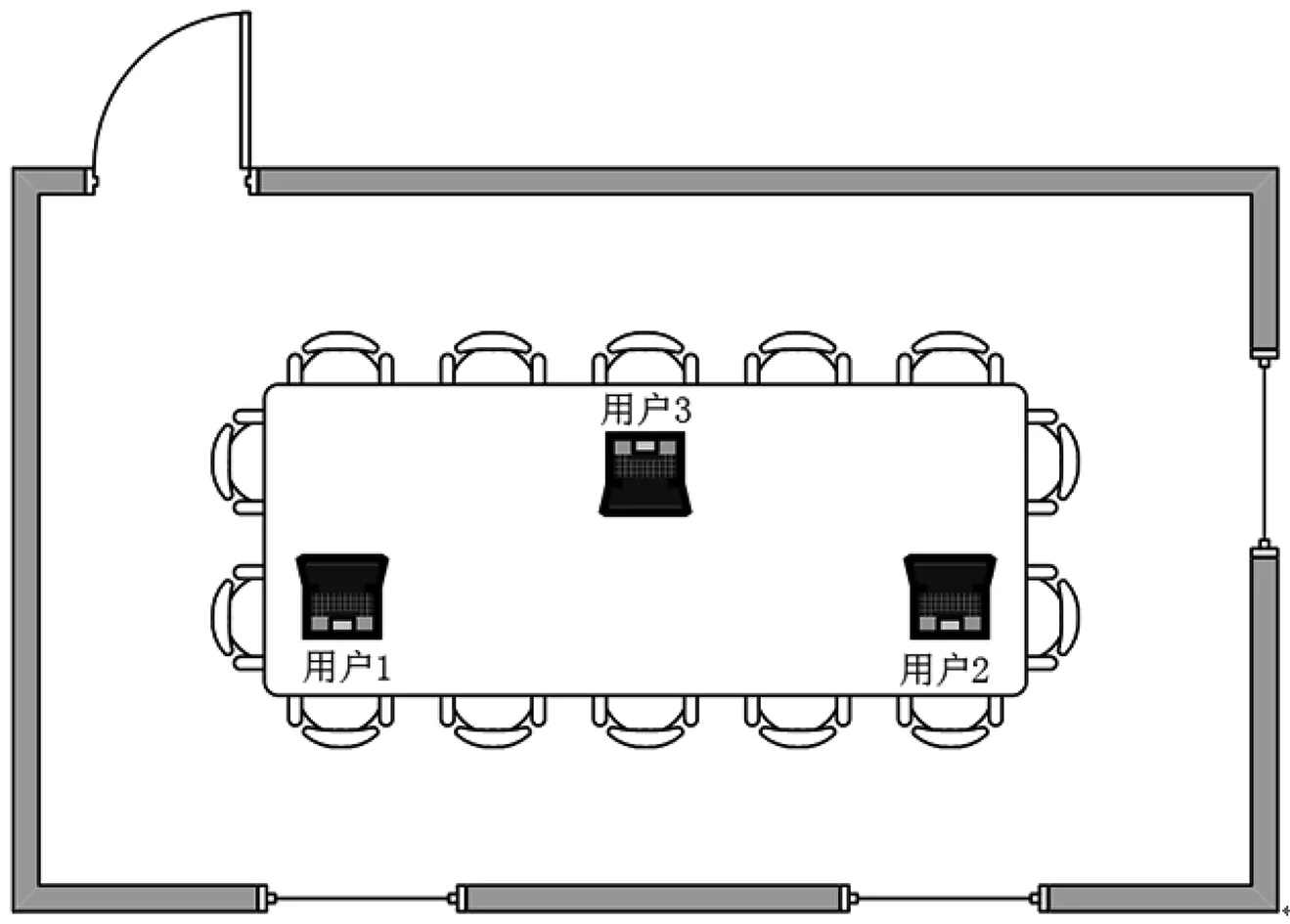
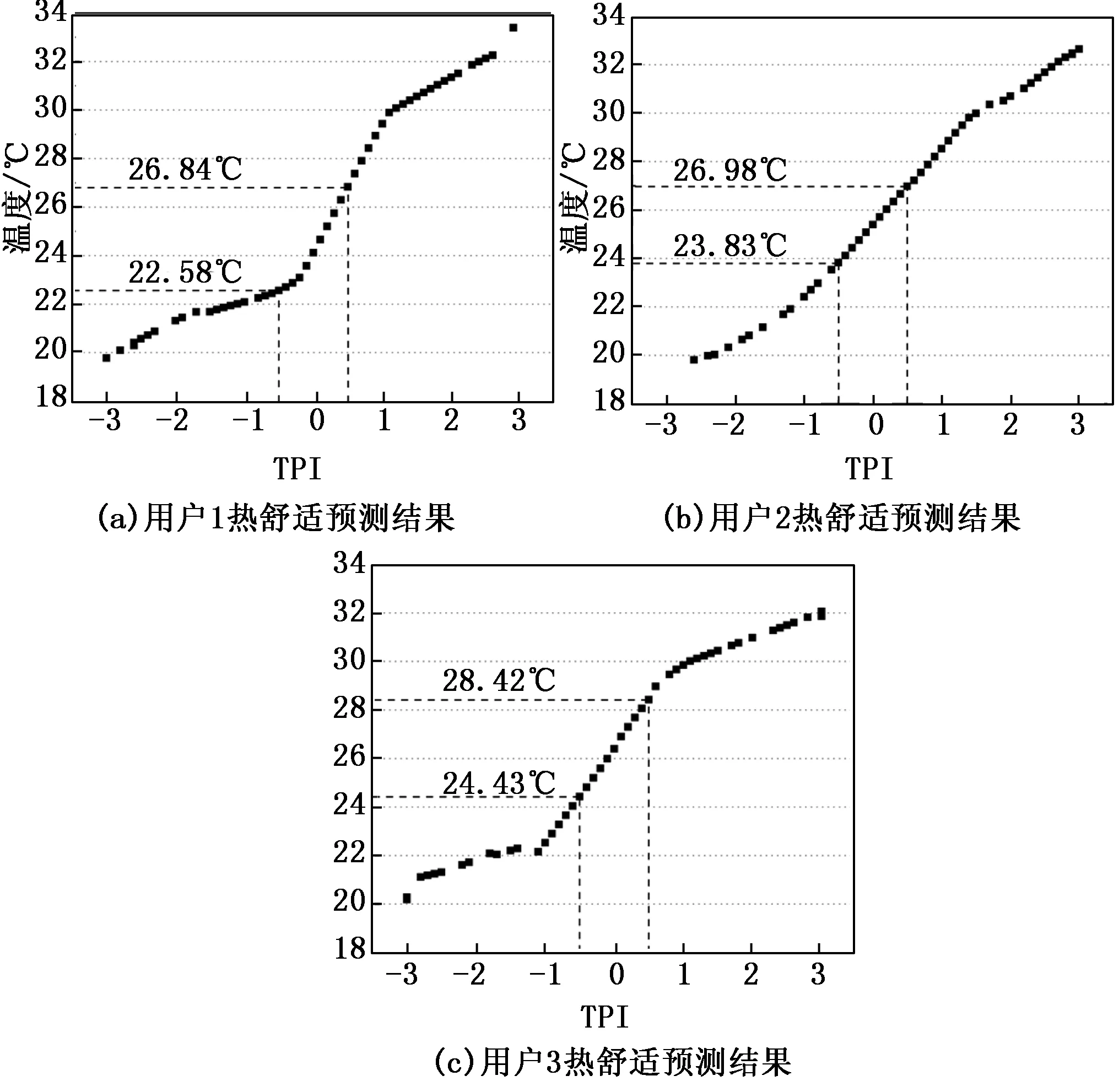
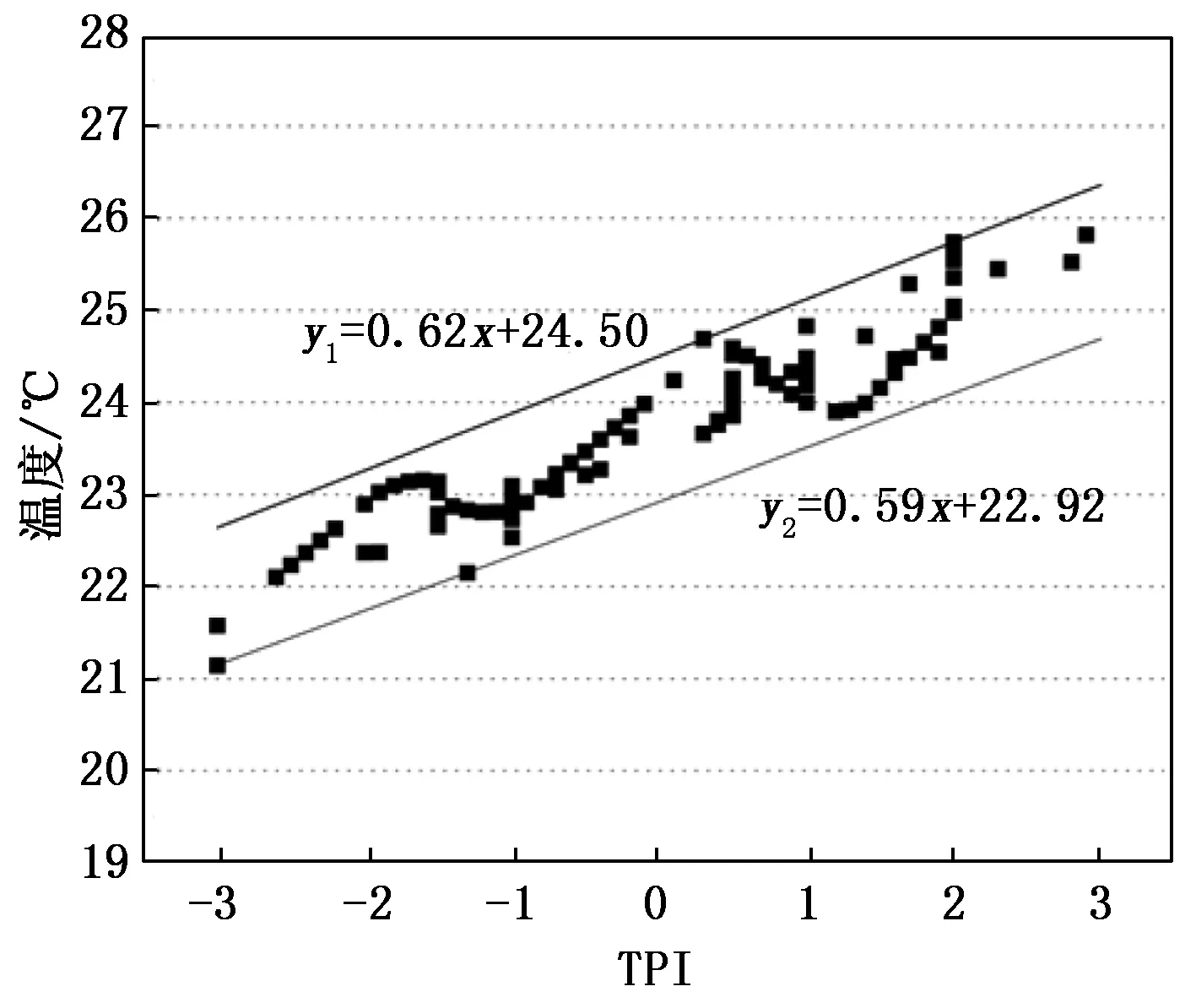
由图7可以看出，当Dthr<0.2时,模型预测输出与交互样本误差相对平稳(根据图6可知，模糊集数大于2)；当0.03

3.2 现场实验研究

为研究DENFIS算法对现场的实用性和仿真实验的有效性，利用本研究开发的移动端智能交互系统进行办公环境用户热舒适现场实验，选取夏季典型气象日工作时段，2019年7月15日至2019年7月25日，上午9：00～12：00，下午2：00～5：00。着装采用统一办公着装，上身为短衬衫，下身为长裤。于西安市某办公建筑会议室进行，该办公室尺寸为6.05 m(长)× 4.95 m(宽)× 3 m(高)，有两个外墙、三扇窗户、一个门。选取三名健康在校大学生作为实验对象，其基本信息如表5所示，在室内的位置如图8所示。

表5 实验对象基本信息

图8 办公会议室平面与人员位置情况

实验内容主要包括室内热环境参数测量及实验对象个人主观交互信息采集两部分。测点位置依据ASHRAE55-2013《人类居住热环境条件》中所规定的“测点部署于受试者胸前20厘米处”进行布置。将采集的现场实验数据清洗后，采用DENFIS算法对以空气温度和TPI组成的样本学习用户热舒适，输出三名实验对象舒适预测结果，如图9所示。

图9 现场实验用户热舒适预测结果

从图9中的用户热舒适预测结果看出，用户1的最佳的热舒适温度为24.12 ℃，舒适温度范围为22.58～26.84 ℃；用户2的最佳的热舒适温度为25.40 ℃，舒适温度范围为23.83～26.98 ℃；用户3最佳的热舒适温度为26.40 ℃,舒适温度范围为24.43～28.42 ℃。由模型推理预测结果可知，个体舒适温差可达5.84 ℃。三名用户的热舒适模型预测值与现场实验交互数据的RMSE分别为0.87 ℃、1.17 ℃、0.88 ℃，均小于仿真误差结果，满足仿真实验结论；且误差也均小于个体间舒适偏好温度的偏差2.6 ℃，满足区分不同个体偏好温度的预测需求，表明在线预测模型在实践应用中可以对个人热舒适进行有效预测并控制误差在可接受范围内。

3.3 多用户热舒适预测研究

为进一步研究在线预测模型对群体热舒适预测的适用性，本文依据ASHRAE全球热舒适数据库II(The ASHRAE Global Thermal Comfort Database II)，对其中群体用户热舒适感数据集中空气温度和TPI的关系进行了分析。首先选取夏季办公建筑24岁女性群体用户的数据集，然后依据该数据集中热偏好、热可接受性和PMV值等信息进行数据清洗，剔除与TPI和空气温度不一致的数据，共获取190组样本数据。采用DENFIS算法对群体用户热舒适进行预测，如图10所示。

图10 群体用户热舒适预测结果

该结果中热感觉指标TPI与室内空气温度以舒适带的形式表现，主要原因是群体用户热舒适感不同，即同一热感觉指标反馈对应于不同温度。群体用户最佳的热舒适区以TPI为0所映射的温度范围进行定义。从图10可以看出，预测结果显示该群体用户最佳舒适温度范围为22.92～24.50 ℃，预测值与群体样本数据间的均方偏差约为1.06 ℃。该误差产生源于群体数据中个人主观反馈热舒适的不确定性以及个体间的衣服热阻和新陈代谢差异性等因素，但误差在1 ℃左右，与现场研究结果一致，误差结果小于个体间舒适偏好温度的偏差2.6 ℃，结论表明预测模型同样对群体热舒适有很好的预测效果。

4 结束语

用户热感觉参数难以检测与获取，并对预测模型的建模带来极大难度。因此本文设计并开发了移动端智能交互系统采集用户热舒适感数据，建立用户学习样本；在此基础上，针对热舒适具有动态变化性问题，将进化聚类算法与Takagi-Sugeno推理模型结合，设计DENFIS算法，构建基于热感觉的在线预测模型；实验结果表明DENFIS算法对热舒适预测主要特征如下：(1)在保证与用户基准模型误差小于0.5 ℃的误差条件下对用户舒适温度范围预测准确率最高可达90.5%，高于传统标准对用户舒适温度预测的准确率56%；(2)不仅能动态建立预测模型，而且在简化建模参数的同时能够有效降低交互过程中干扰因素造成的误差；并在个体与群体用户样本数据中对热舒适进行有效预测并控制误差在个体间舒适偏好温度的偏差2.6 ℃内；(3)在样本数据聚类数为5时，预测模型可得到最佳预测结果。因此该方法基于热感觉信息对用户舒适温度预测具有很高准确度，为空调温度的设定具有实际应用价值。