不同时间尺度下新能源联合发电特性及最优配比

辛业春，徐广健，张一峰，杨 勇，董 倩

(东北电力大学，吉林 吉林 132012)

随着经济的迅速增长，人们对能源的需求也越来越多，而化石能源危机和全球气候变暖等因素，又加剧了社会发展和能源需求之间的矛盾，风电和光伏等新能源为化石能源危机带来了曙光[1-2]。2017年，全国风电年发电量3 057×108kW·h，弃风电量419×108kW·h，弃风率12%，光伏年发电量1 182×108kW·h, 弃光电量73×108kW·h，弃光率6%[3]。风能具有波动性、随机性和不可控制性，大规模并网威胁着电力系统的安全稳定运行[4-6]。光伏受温度光照等气候影响，存在并网利用率不高，电能质量治理成本高等问题[7-9]。文献[10]定义风电场负荷变化的平稳性、一致性和互补性指标，实现对风电场功率变化的评估，单一能源的发电不能满足并网的需求。文献[11]分析单台风电机组、单个风电场及风电场群输出功率在不同时间尺度下的波动特性。文献[12]通过历史数据从不同的维度对风电输出特性进行了综合分析，包括日输出特性、季节输出风电概率分布。文献[13]分析了风电出力相关性对计算风电容量可信度的影响，通过Copula函数提高对多风电场容量可信度的快速计算。文献[14]通过对光伏出力的波动数据进行概率密度拟合，分析不同时间尺度的光伏出力波动特性和随机分布特性，仅考虑了单一能源的出力特性。文献[15]指出大型光伏电站出力随机波动性对接入电网的电能质量及稳定性带来了不利影响。文献[16]建立光伏模型和仿真，对多个光伏电站监测数据研究分析，总结出光伏电站随季节天气变化运行规律。文献[17]分析了风电和光伏功率的联合相关性，仅以功率波动大小进行衡量，计算方法具有一定的局限性。上述文献都针对单一新能源发电特性，而单一新能源发电具有波动性和不可靠性，多种新能源联合发电能够解决该问题。

本文基于比利时新能源基地历史数据，研究不同时间尺度下大型风电-光伏基地的风电和光伏联合出力特性问题。不同地区有不同的风电和光伏配比，通过历史天气对风电和光伏发电量预测，再结合本文的究方法可为新能源待开发地区新能源规划和建设提供参考依据。

1 新能源联合发电评价指标

1.1 多时空尺度下风电和光伏的波动性

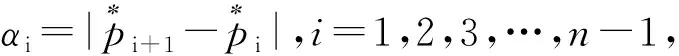
(1)

当β的绝对值越接近0时，说明功率信号此时的变化越小，可认为功率信号变化没有波动；当β的值越大，反映功率信号波动性越大。本文利用分辨率为15 min的真实数据作为基础，通过累积积分并求平均值得到各时间尺度发电数据。

1.2 多时空尺度下风电和光伏的相关性

风电和光伏之间的相关性是指两个变量之间的关联程度，在同一时间内，风电场和光伏电场之间的相关性强时，则风电和光伏之间的互补特性较弱，用相关系数r来评判相关性的强弱。

(2)

其中，r为相关系数，用来度量两个变量间的线性关系，相关系数绝对值|r|在0.8～1，认为X和Y是强相关的，在0.5～0.8，是一般相关的，在0.3～0.5，是弱相关，在0～0.3，是没有相关的；Cov(X,Y)为X和Y的协方差，Var[X]是X的方差，Var[Y]是Y的方差。

1.3 多时间尺度下风电和光伏的互补性

不同时间尺度下风电和光伏之间互补程度有一定的差异，风光互补性主要体现在，风电和光伏发电受天气影响较强，风机在白天受风力影响出力小，夜间受风力影响出力较强，与光伏白天发电强，夜间不发电相互补。因此应该着重研究日时间尺度下的互补特性。二者的波动变化率分别为 {α1j}、{α2j}，j=1,2,3,…,n-1，定义集合:

B={γj|γj=|α1j-α2j|}

当γj=0时，说明两功率信号此时的变化方向相同、速率相等，认为两信号变化是一致的；当γj>0时，说明两个功率信号变化不一致，γj大小反映此时两风电功率信号变化不一致的程度。为考察某时间内变化不一致程度，定义指标：

(3)

δ越接近于0，说明两信号在考察时间内的变化特性越一致，互补性越差；反之，δ越大，说明两信号变化的不一致性越高，互补性越强。

2 能源基地概况及算例分析

本文以比利时新能源基地的风电数据和光伏数据为基础，时间段为2017年9月30日到2018年9月30日，分辨率为15 min。由于有丢失数据和数据异常的现象，均由其提供的预测数据代替异常数据。

典型日输出特性分析：风电在冬季日输出的功率最高，夏季日输出的功率最低；光伏发电与风电相反，在夏季日发电达到最大，冬季日发电最低。风电输出没有规律，相对于光伏的波动性小；光伏发电时呈对称性，春夏秋三季有剧烈的上升和下降阶段。

15 min时空输出特性分析：风光联合发电系统年持续功率曲线是将系统一年中的功率按从大到小的顺序排列的出力曲线，系统年持续功率曲线能够体现一年新能源产生电能水平。比利时新能源基地联合发电减小极大发电和极小发电时间，使发电波动更平稳。

2.1 联合发电特性分析

表1是新能源发电在不同时间尺度下的波动率，从表中可以发现随着时间尺度的增加新能源发电波动率增加。光伏波动率大于风电波动率，是因为风机转动时具有转动惯性，在短时间尺度下风机转动惯量很难改变，因此风电在短时间尺度下风电波动率小，随着时间尺度的增加，风机转动惯性难以显现，风电波动率增加；光伏发电不具有“惯性”并且有夜间“断电”的现象，因此光伏发电在短时间尺度下有明显的波动，在日时间尺度下波动很小。

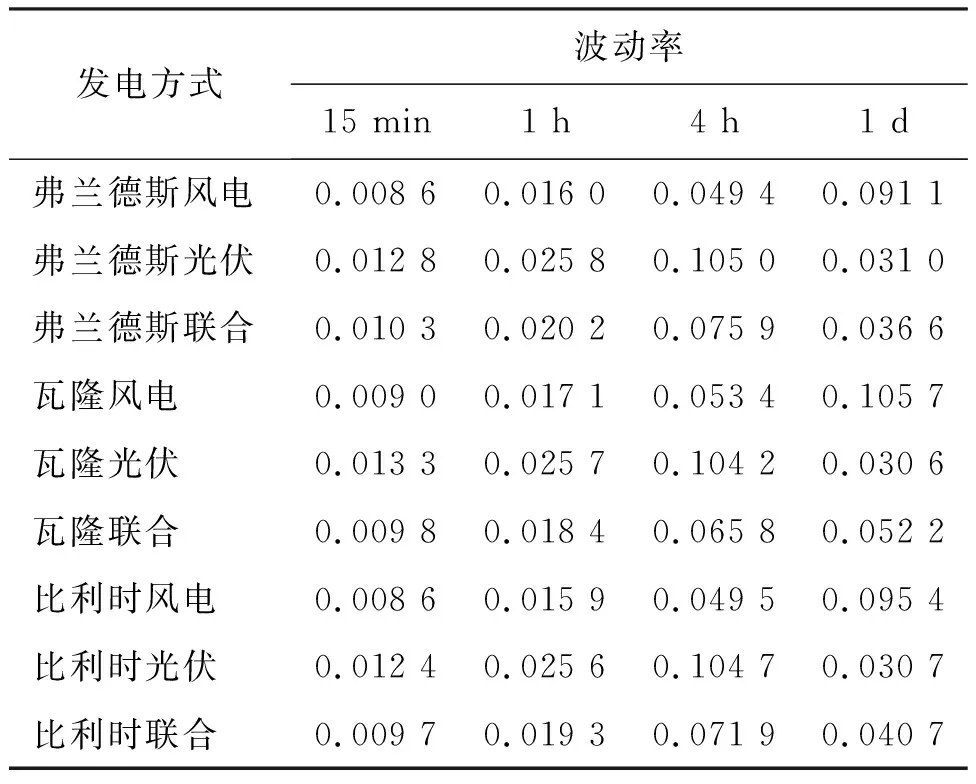
表1 不同时间尺度下新能源发电波动率

表2是风电场和光伏电场之间交叉组合的相关系数，表中W1为弗兰德斯风电场；W2为瓦隆风电场；Ph1为弗兰德斯光伏电场；Ph2为瓦隆光伏电场。从该表可以看出，在任何时间尺度下，单一新能源场之间都存在强相关性，风电和光伏电之间不相关或存在负相关，从侧面可以体现风电和光伏之间的存在互补性，单一新能源电场之间具有同时性。

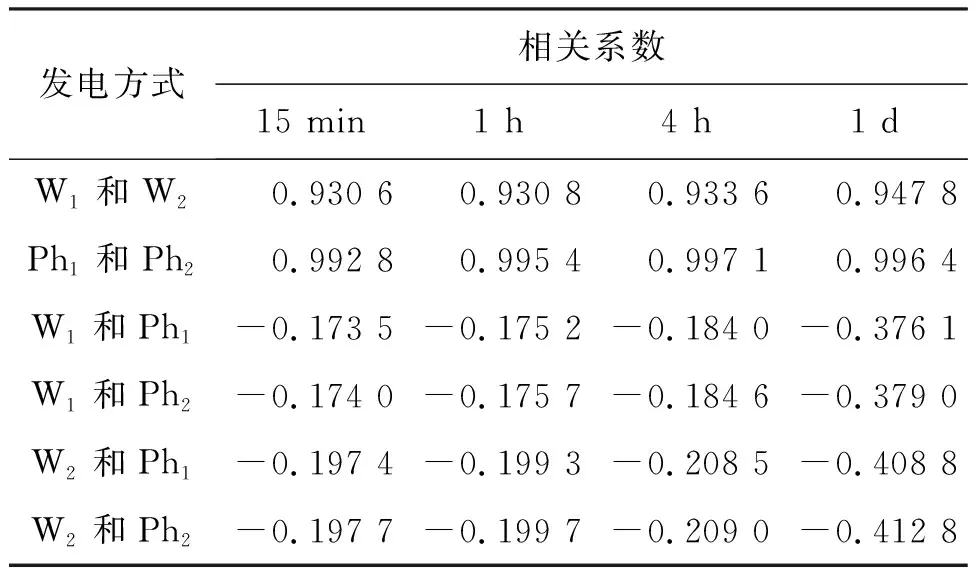
表2 风电和光伏交叉组合的发电相关性

表3是风电场和光伏电场之间交叉组合发电的互补性。从该表可以看出，随着时间尺度的增加联合发电互补系数增加，互补性增强，在不同时间尺度下，单一新能源之间联合发电的互补性系数最小，不同区之间风光联合发电的互补性指标都是最高的，风光联合发电可以减小同时发电的概率，广域风电和光伏联合发电有更好的互补性。

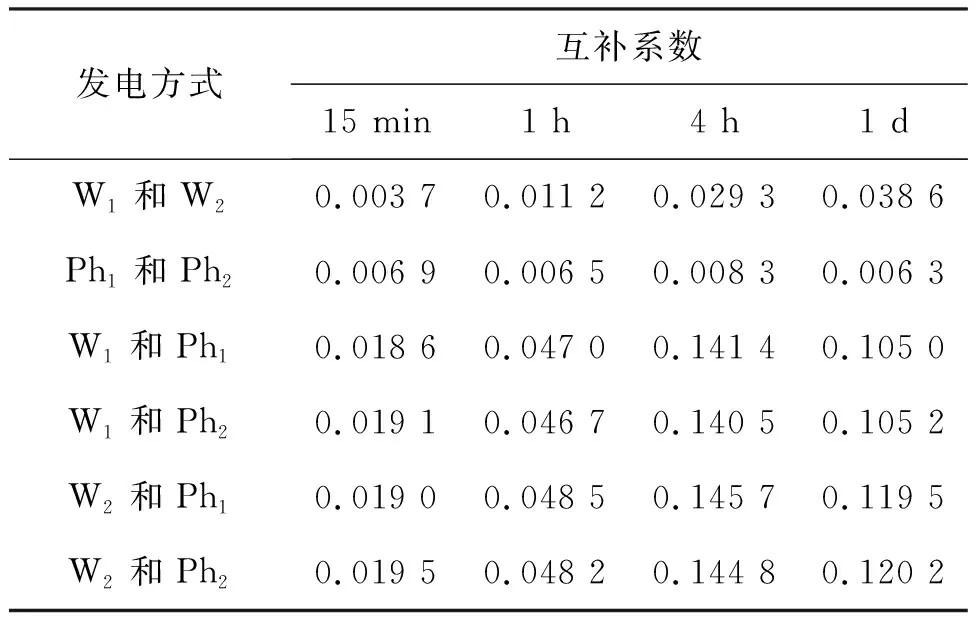
表3 风电和光伏交叉组合发电互补性

2.2 风光联合发电容量最佳配比

为提高风光并网率，本文研究风电和光伏两种新能源在日时空尺度下的不同场景的最佳配比。首先投入比利时全部风电容量，然后逐渐增加光伏容量比重，观察比重对年发电时间、日发电波动率和年累积发电的影响，得到风电容量和光伏容量最佳配比。图1是不同风光容量配比对年累积发电时间的影响，是通过风光联合发电系统年持续功率最大值得到的年发电时间。由于风电和光伏之间存在互补性，所以当光伏容量逐渐增加之后，光伏弥补风电“断电”时间，增加新能源年累积发电时间。当光伏在经线上布满整个地域，则新能源联合发电时间常数达到饱和，因此，光伏容量和风电容量比小于1时，对联合发电系统的年累积时间是有很大的提升，比例大于1时，年累计发电时间趋于饱和状态。

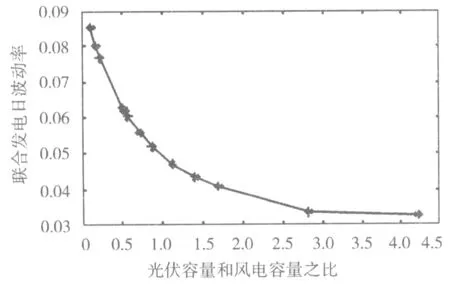
图1 光伏和风电容量配比对年累计发电时间的影响

图2是不同风光容量配比对日波动率的影响。随着光伏容量占的比重越来越高，风光联合发电日波动率逐渐降低，光伏与风电容量配比在0.1～1.0，日波动率快速下降，光伏和风电配比在1.68～4.70，日波动率缓慢下降并趋于稳定。增加光伏容量的比重能够减小联合发电的日波动率。

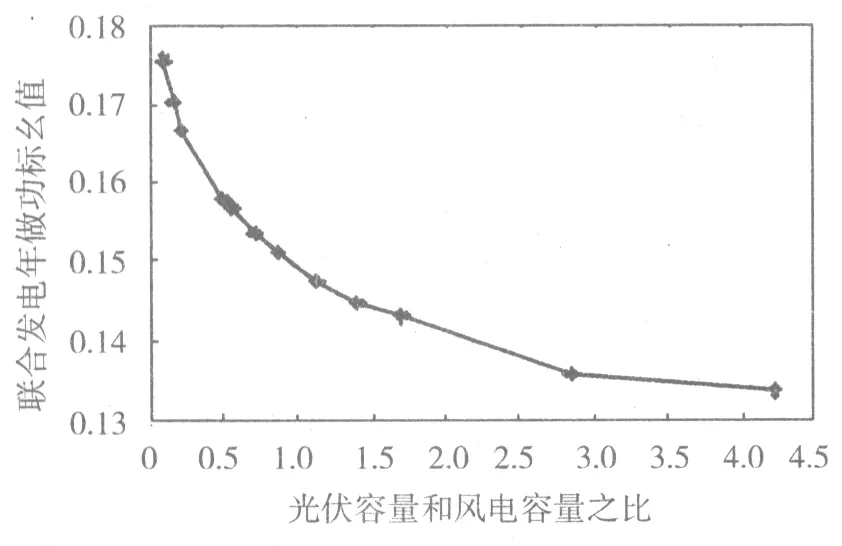
图2 光伏和风电容量配比对日波动的影响

图3是不同风光容量配比对年累积能量标幺值的影响，该图是通过Matlab对风光不同配比下联合系统年持续功率曲线做积分得到的年累积做功，纵坐标是曲线累积做功的标幺值，其值大小代表系统年做功量的多少。随着光伏比重的逐渐增加，联合发电年做功标幺值逐渐降低。光伏容量与风电容量配比在0.1～1.0，年做功标幺值快速下降，光伏和风电配比在1.68～4.70，年做功标幺值缓慢下降并趋于稳定。

综上所述，风电容量和光伏容量最佳配比区间是在1∶1至1∶1.68之间，该比例区间既能满足年发电时长和较小的日发电波动率，也有一个良好的年发电量。

3 结论

本文基于比利时新能源基地数据，研究各时间尺度下的风电和光伏及其联合输出特性。建立各时空尺度下风电和光伏输出波动性、相关性和互补性的评价标准，通过约束条件得到风光容量最佳配比。并得到如下结论。

a.通过实际数据的分析，风电能够弥补光伏夜间“断电”的现象，在夏季和冬季风电和光伏具有明显的互补特性。

b.由于短时间尺度下风电机组具有惯性，所以风电的波动率比光伏波动率小，风电和光伏联合发电增加了新能源的容量减小光伏发电的波动率；大规模新能源联合发电能能够有效减小新能源发电波动率。

c.在任何时间尺度下风电场和光伏电场之间存在负相关或不存在相关。风电和光伏之间的互补性高于单一类型电场之间的互补性，并随着时间尺度在增加互补性越强。

d.通过改变现有风机装机容量和光伏装机容量的比例对年累积发电时间、发电波动率和年累积发电标幺值的影响，得到风电容量和光伏容量的最优配比区间。