ON THE ASYMPTOTIC SPECTRUM OF A TRANSPORT OPERATOR WITH ELASTIC AND INELASTIC COLLISION OPERATORS∗
2020-08-02AbdulMajeedALIZERIKhalidLATRACH
Abdul-Majeed AL-IZERI Khalid LATRACH
Universit´e Clermont Auvergne, CNRS, LMBP, F-63000 Clermont-Ferrand, France
E-mail: Abdul Majeed.Al izeri@uca.fr; khalid.latrach@uca.fr
Abstract In this article, we investigate the spectral properties of a class of neutron transport operators involving elastic and inelastic collision operators introduced by Larsen and Zweifel [1]. Our analysis is manly focused on the description of the asymptotic spectrum which is very useful in the study of the properties of the solution to Cauchy problem governed by such operators (when it exists). The last section of this work is devoted to the properties of the leading eigenvalue (when it exists). So, we discuss the irreducibility of the semigroups generated by these operators. We close this section by discussing the strict monotonicity of the leading eigenvalue with respect to the parameters of the operator.
Key words Compactness properties; transport operator; abstract boundary conditions;asymptotic spectrum; irreducibility; leading eigenvalue
1 Introduction
The purpose of this work is to discuss the spectral properties of the following neutron transport operator involving elastic and inelastic collision operators introduced by E.W.Larsen and P. F. Zweifel [1]:

where (x,v) ∈(Ω×V), Ω is a smooth open subset of RN, µ(·) is a positive Radon measure on RN, such that µ(0) = 0, and V denotes its support (V is called the space of admissible velocities). The function ϕ(x,v)represents the number density of particles having the position x and the velocity v. The function σ(·)is called the collision frequency and the functions kc(·,·,·),ke(·,·,·,·), and(·,·,·,·),j = 1,···,l, denote the scattering kernels of the operators Kc, Ke,and(called classical, elastic, and inelastic collision operators, respectively). In our framework,the boundary conditions are modeled by

where ϕ−(resp. ϕ+)denotes the restriction of ϕ to Γ−(resp. Γ+)with Γ−(resp. Γ+)standing for the incoming(resp. the outgoing)part of the phase space and H is a bounded linear operator from a suitable space on Γ+to similar one on Γ−. The operator AHdescribes the transport of populations of particles (neutrons, photons, molecules of gas, etc.) in the domain Ω.
It should be noticed that, in kinetic theory of gas where we must describe the interaction of gas molecules with the boundary of the region where the gas flows, the theoretical problem is to relate the distribution function of molecules leaving a solid surface to the distribution of the molecules arriving at the same surface. However, the boundary conditions which describe this interaction are very complex because the reaction of a gas molecules with a wall is so complicated. This is due, mainly, to our lack of knowledge of the structure of surface layers of solid bodies, and hence of the effective interaction of the gas molecules with the wall (see, for example, [2]). Nevertheless, a model which is often used consists in supposing that a part of the outgoing flux is re-emitted in a deterministic way (specular reflection), whereas the other part is re-emitted in random directions (diffuse reflections).
Note that in order to describe the properties of the solution(when it exists)to the Cauchy problem

the knowledge of the spectrum of the operator AHis of fundamental importance. This is because of the fact that, in general, the solution is not constructive (we have the existence of the solution via general arguments like the Hille-Yosida theorem). So,a lot of works concerning spectral properties of the transport operators were done by many authors (see, for example,[1, 3–12] and the references therein).
In this model, the collision operator is given by K =Kc+Ke+Kd, where Kcdenotes the collision operator involved in the classical neutron transport theory (see, for example, [5]). It is given by
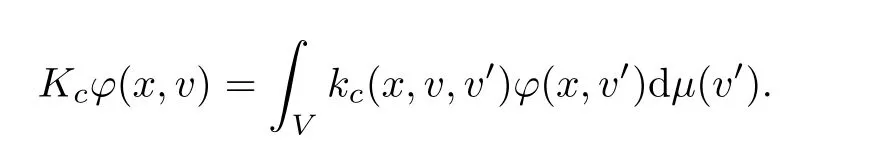
The operator Kdis called the inelastic collision operator, and it is given by

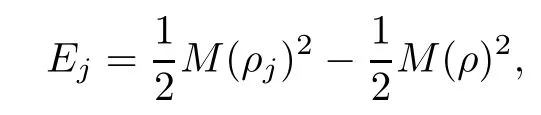
while M stands for the mass of neutron.
Finally, Keis called the elastic collision operator. It is given by

It describes the collisions which do not vary the kinetic energy of neutrons. It acts only through the angular part of the velocity variable.
Let us notice that the spectral properties of the operator AHwas first studied by E. W.Larsen and P.F. Zweifel[1] in the space L1. It was considered afterwards by M.Sbihi [6, 7]for vacuum boundary conditions H =0 (zero incoming flow). This work is inspired and motivated by [1, 6, 7] and is intended to complete the results of the preceding works to the case of rentry boundary conditions () in the spaces Lp(Ω×V) with (1 ≤p<∞).
In the next section, we introduce the functional setting of the problem and establish some preliminary facts required in the rest of this article. As it is well known in neutron transport theory, the averaging in velocities provides the compactness of the operatorSo, the goal of Section 3 is to establish similar compactness properties involving the various parts of the collision operator K, which are in the basis of the description of the asymptotic spectrum of the operator AH. The main results of this section are Theorems 3.10 and 3.16. Unlike [1, 6, 7] and as in [13], we discuss compactness properties for abstract boundary conditions on Lp(Ω×V,dxdµ(v)),(1 ≤p < ∞) for the class of regular collision operators Kc[4]. Our main result is that if Kcis regular and the hyperplanes of RNhave zero µ-measure (that is, for each e ∈SN−1,µ{v ∈RN, v.e = 0}= 0,where SN−1denotes the unit sphere of RN), then the operators Kc(λ −TH−Kd−Ke)−1and(λ −TH−Kd−Ke)−1Kcare compact on Lp(Ω×V,dxdµ(v)),(1 < p < ∞) (see Proposition 3.5) and the operator Kc(λ −TH−Kd−Ke)−1Kcis weakly compact on L1(Ω×V,dxdµ(v))(see Proposition 3.15). Moreover, in Corollary 3.9, we give sufficient conditions guaranteeing the invariance of the essential spectrum of TH+Ke+Kdin the case where p ∈(1,+∞). This result is open for p=1.
As a consequence of compactness results of Proposition 3.5 and Proposition 3.15, we have

consisting of,at most,isolated eigenvalues with finite algebraic multiplicity on Lp(Ω×V,dxdµ(v))with 1 ≤p<∞. If the set given by(1.4)is not empty,then the operator TH+Kc+Kd+Keadmits a real leading eigenvalue. In neutron transport theory,it is important to know if the leading eigenvalue is strictly dominant or not. So, the irreducibility of the C0-semigroup generated by TH+Kc+Kd+Kewill be discussed in Subsection 4.1. We give sufficient conditions in terms of H and Kcensuring the irreducibility of the C0-semigroup generated by TH+Kc+Kd+Ke,which implies that the leading eigenvalue of TH+Kc+Kd+Ke(if it exists) is strictly dominant with multiplicity 1 and the associated eigen-function is strictly positive. The problem concerning the strict monotonicity of the leading eigenvalue with respect to the parameters of the transport equation is the purpose of Subsection 4.2. We use a comparison result of spectral radius of positive operators (Theorem 2.8). It permits us to show that the leading eigenvalue increases strictly with respect to H and Kc.
NotationLet X be a Banach space and S a linear operator on X. As usually, we denote by σ(S), σp(S), and ρ(S) the spectrum, the point spectrum, and the resolvent set of S,respectively. An eigenvalue λ∗of S is called the leading eigenvalue of S if it is real and there exists η >0 such that

The set of all bounded linear operators on X will be denoted by L(X). If S ∈L(X), we denote by rσ(S) the spectral radius of S. If S is an unbounded linear operator, the spectral bound of S is defined by

2 Preliminaries
Let Ω be a smooth open bounded subset of RNand let µ(·) be a positive Radon measure on RNsuch thatµ(0)=0. We denote by V the support ofµand we refer to V as the velocities space. We note that the boundary of the phase space Ω×V is written as ∂Ω×V :=Γ+∪Γ−∪Γ0,where Γ±= {(x,v) ∈∂Ω×V,±v.νx> 0} and Γ0= {(x,v) ∈∂Ω×V, v.νx= 0}, where νxstands for the outer unit normal vector at x ∈∂Ω. We will suppose throughout this article(which is a reasonable hypothesis) that the measure of Γ0with respect to dγxdµ(v) is of zero(dγxbeing the Lebesgue measure on ∂Ω). Let p ∈[1,+∞) and define the functional space by

A suitable Lp-space for the traces of functions in Wpis

For ϕ ∈Wp, we denote the traces of ϕ (when there exist) by ϕ−on Γ−and ϕ+on Γ+respectively. Note that, in general, these traces do not belong to Lp,±but ly only in the spaceor more precisely in a certain weighted Lp-space. Define

We have the following lemma on the traces [14–16].
Lemma 2.1Let p ∈[1,∞) and ϕ ∈Wp. If ϕ+∈Lp,+, then ϕ−∈Lp,−and vice versa.
In other words, we have the identity

Definition 2.2Let (x,v)∈×V. We set
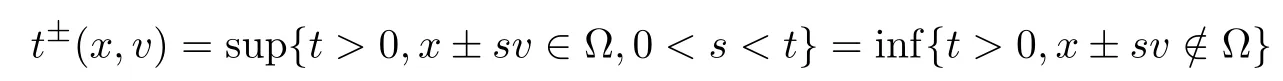
and

Hence,for(x,v)∈Γ±,one has t±(x,v)=0,t∓(x,v)>0 and in all cases x−t−(x,v)v ∈Γ−.The number t∓(x,v)is the time required by a particle having the position x ∈Ω and the velocity±v ∈V to go out Ω.
The boundary conditions may be written abstractly as an operator H relating the incoming and the outgoing fluxes
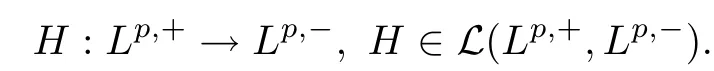
The streaming operator TH, with domain including the boundary conditions, is defined by
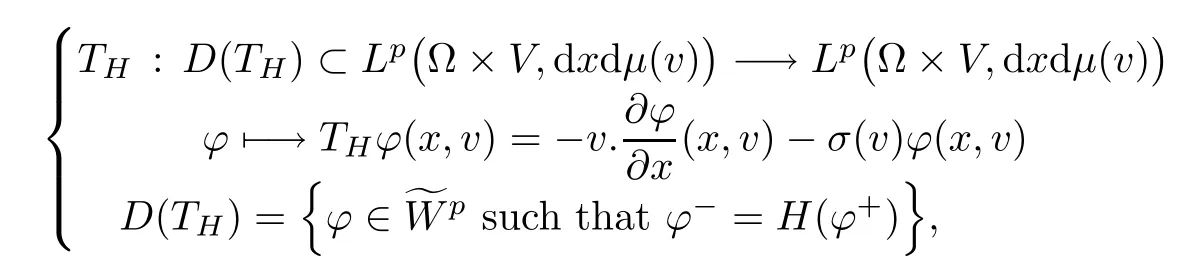
where the collision frequency is assumed to be essentially bounded on V, that is

and consider the resolvent equation for the operator TH,

where λ is a complex number and the unknown ψ must be sought in D(TH). Proceeding as in[13], ones sees that, for Reλ>−, the solution of Equation (2.1) is formally given by

Moreover,for (x,v)∈Γ+, (2.2) becomes

where τ(x,v)=t+(x,v)+t−(x,v). We now introduce the following operators

and
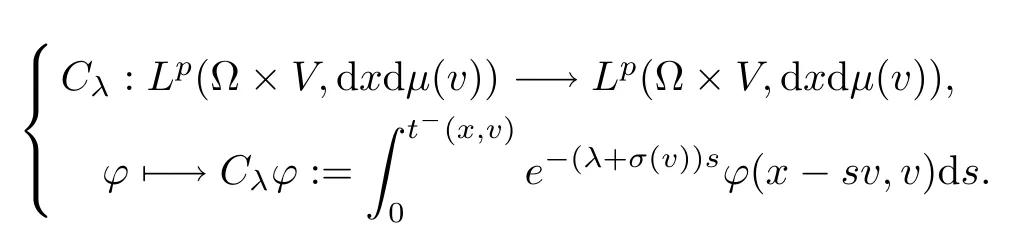
These operators are bounded on their respective spaces [13]. In fact, the norms of Bλand Cλare bounded above, respectively, byand (Reλ+)−1, where q denotes the conjugate of p. Moreover, the operator Mλu = [Bλu]|Γ+is a contraction and Gλϕ= [Cλϕ]|Γ+is bounded with norm less than
Remark 2.3It is clear that, for any real λ such that λ > −the linear operators Mλ, Bλ, Gλand Cλare bounded and positive (in the lattice sense). Indeed, as 0 ≤σ(·) ∈L∞(V,dµ(v)), the operators Mλand Bλare multiplcation operators by nonnegative functions,so Mλ(resp. Bλ) maps the positive cone of(resp.) into the positive come of(rep.Lp(Ω×V,dxdµ(v)). This proves the positivity of Mλand Bλ. The same argument shows that the operators Gλand Cλare positive too.
Using these operators and the fact that ψ must satisfy the boundary conditions, Equation(2.3) becomes

The solution of this equation reduces to the invertibility of the operator (I −MλH). So, if(I −MλH)−1exists(in particular if rσ(MλH)<1 or if there exists a real τ such that for all λ in the complex half-planewe havethen

On the other hand, Equation (2.2) can be written in the form ψ =BλHψ++Cλϕ. Substituting (2.4) in this equation, we get ψ = BλH(I −MλH)−1Gλϕ+Cλϕ. Accordingly, for any λ ∈C such that Reλ>−, the resolvent of the operator THis given by

Remark 2.4We know from the calculations above that if λ is a real number such that λ > −then the operator I −MλH is invertible. Hence, λ ∈ρ(TH) and (λ −TH)−1is given by (2.5). Clearly, if H is positive in the lattice sense, then the operator (I −MλH)−1is also positive. Because, for each real λ > −, the operators Mλ, Bλ, and Gλare bounded positive linear operators,we get

We recall the following result established in [13].
Lemma 2.5Let p ∈[1,∞). If≤1, then for any λ satisfying Reλ>−, we have

NotationIn the remainder of this article, we shall denote bythe operator Ke+Kd.
Remark 2.6It should be noticed that from physical view point, the operators H, Kc,Keand Kdare positive (in the lattice sense). That is
• H maps the positive cone of Lp,+into the positive cone of Lp,−and
• Kc, Ke, and Kdmap the positive cone of Lp(Ω×V,dxdµ(v))) into itself.
Let λ be a complex number and let ϕ be given function of Lp(Ω×V,dxdµ(v)). We consider the equation

where unknown function ψ must be sought in D(TH). It is clear that if Reλ > −, then Problem (2.6) can be written in the form

and therefore, by Lemma 2.5, we have
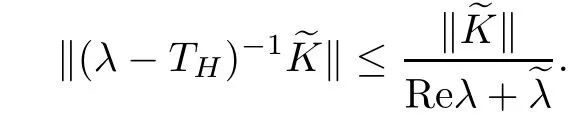
So, for λ such that Reλ large enough, we getand therefore the operator I −(λ −TH)−1is invertible. Consequently, (2.7) may be written as

This shows that

and, for such λ, we have
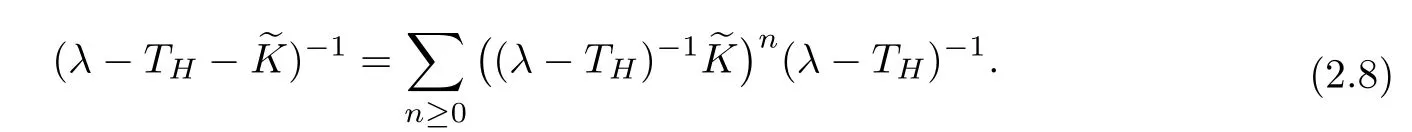
Furthermore, easy calculations using Lemma 2.5 and Neumann series give

For the reader convenience,we recall some definitions and results on the essential spectrum and the essential type required in the sequel.
Let X be a Banach space, a closed densely defined linear operator A with domain D(A).We define the essential spectrum of A by

where K(X) stands for the ideal for all compact operators on X. As a simple consequence of the previous definition, we have the followings:
(i) the set σess(A) is closed, and
(ii) if C ∈K(X), σess(A+C)=σess(A).
We now recall the following result which we shall use in the sequel (we refer, for example,to [17, Theorem 4.7, p.17]).
Theorem 2.7Let X be a Banach space and let A,B be two closed linear operators with dense domains on X. If for some λ ∈ρ(A)∩ρ(B), the operator (λ −A)−1−(λ −B)−1is compact, then σess(A)=σess(B).
Let X be a Banach lattice and let A, B ∈L(X) be two positive operators. It is clear that if A ≤B, then rσ(A) ≤rσ(B). The next result owing to I. Marek [18, Theorem 4.4] provides sufficient conditions under which the latter inequality is strict. More precisely, we have
Theorem 2.8Let A and B be two positive operators satisfying A ≤B and. If A is not quasinilpotent, and B is irreducible and power compact(that is,Bnis compact for some integer n ≥1), then
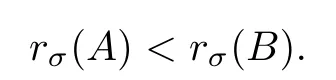
3 Compactness Properties and Their Consequences
In article[1],E.W.Larsen and P.F.Zweifel discussed the spectral properties of the operator TH+Ke+Kd+Kcwith vacuum boundary conditions (H = 0) in the space L1. In [7], this analysis was extended to Lp-spaces with p ∈[1,+∞). Our objective here is to complete the results of these two works by considering,in particular,the case where the incoming flow is not zero, that is, H≠=0. Here, we shall split our discussion into two cases: p ∈(1,+∞) and p=1.
Remark 3.1We note that the asymptotic spectrum of the streaming operator THand the operator TH+Kcwas studied in [21] (for the definition of Kc, see below). In this article,we shall study the asymptotic spectrum of the operator TH++Kc.
3.1 Case p ∈(1,∞)
In this subsection, we shall be interested in the asymptotic spectrum of the operator TH++Kcon the spaces Lp(Ω×V,dxdµ(v)) with p ∈(1,+∞).
Let us first note that the collision operator Kcis, in general, an integral operator with respect to velocities. It has the form

where ϕ ∈Lp(Ω×V,dxdµ(v)). As Kcis local for x ∈Ω, one can define the mapping by

where

We suppose that Kc(·) is strongly measurable, that is, for all g ∈Lp(V,dµ(v)),

is measurable, and that the mappingis essentially bounded. It follows from the separability of the spaces Lp(V,dµ(v)) (1 For more details, we refer to [5, Section 1]. In this work, the operator Kcis required to be compact with respect to velocities and depends smoothly on the space variable. So,we will use the concept of regular collision operators introduced in [4] (see also [5]). Before introducing the definition of this class of operators, we first recall the definition of collectively compact operators [19]. Definition 3.2Let X and Y be two normed spaces and denote by B the closed unit ball of X. A set C of L(X,Y) is said to be collectively compact, if and only if the set Definition 3.3We say that Kcis a regular operator on Lp(Ω×V,dxdµ(v))(1 (a) {Kc(x):x ∈Ω} is a set of collectively compact operators on Lp(V,dµ(v)), that is,is relatively compact in Lp(V,dµ(v)); (b) For every ϕ′∈Lq(V,dµ(v)),is relatively compact in Lq(V,dµ(v)), where Lq(V,dµ(v)) is the dual space of Lp(V,dµ(v)) and We shall assume that the measure µ satisfies We first recall the following result obtained in [13]. Lemma 3.4If Kcis a regular collision operator andµsatisfies the hypothesis(A1), then the operators Kc(λ −TH)−1and (λ −TH)−1Kcare compact. Next, we put It should be noticed that Proposition 3.5Let λ ∈S. If the condition(A1)is satisfied and Kcis a regular collision operator, then Kc(λ −TH−)−1and (λ −TH−)−1Kcare compact. ProofLet us notice that by duality,we have[((λ−TH−)−1)∗]∗=(λ−TH−)−1Kc.So,according to Schauder’s theorem(see,for example,[20, p.282]),it is enough to consider the operator The compactness of Kc(λ −TH−)−1follows from Lemma 3.4. Before going further, we first give the following definition. Definition 3.6We denote the asymptotic spectrum of the operator TH++Kcby σas(TH++Kc) and it is defined by Let λ ∈σas(TH++Kc) and define the operator valued function Remark 3.7Let us observe that, for any λ ∈S ∩R, equation (3.3) implies that Hence, by Remarks 2.4 and 2.6, we infer that (λ −TH−)−1is a positive operator. Now,using the positivity of Kc, we conclude that, for any λ ∈S ∩R, F(λ) is a positive operator. Lemma 3.8Let p ∈[1,+∞)and let Kcbe a regular collision operator. Assume that the conditions of Proposition 3.5 hold true, then the map is continuous and strictly decreasing. ProofThe proof may be modeled in the same way as that of Lemma 7.4 in [21], so it is omitted. The following result is an immediate consequence of Proposition 3.5. Corollary 3.9Assume that the hypotheses of Proposition 3.5 hold true. Then, ProofLet ψ ∈Lp(Ω×V,dxdµ(v)), λ ∈S and consider the problem where the unknown function ϕ must be sought in D(TH++Kc). If λ ∈S, then (3.4) may be written in the form Making use of equation (2.8), we get Moreover, according to Proposition 3.5, for all λ ∈S, F(λ) is compact. Using the estimate(2.9), we obtain Using estimate (3.5), on sees that, for such λ, the operator (I −F(λ)) is invertible (in fact, we haveHence, and therefore, Now,the compactness of(λ−TH−)−1Kcimplies that(λ−TH−−Kc)−1−(λ−TH−)−1is compact. Next, applying Theorem 2.7, we get the desired result. Theorem 3.10If the hypotheses of Proposition 3.5 hold true, then σas(TH++Kc)consists of, at most, isolated eigenvalues with finite algebraic multiplicities. Moreover, if, then TH++Kcadmits a real leading eigenvalue λ∗>s(TH+). ProofWe know from the proof of Corollary 3.9 that,for any λ ∈S,we have the estimate So, for any λ0∈S such that Re λ0is large enough, the operator (I −F(λ0)) is invertible.Next, using the fact that F(·) is a compact-valued function on S (cf. Proposition 3.5) and S is connected, it follows from Gohberg-Smulyan’s theorem (see, for example, [22, Theorem 11.4]or [23, Theorem VI.14]) that (I −F(λ)) is invertible for all λ belonging to SD, where D is a countable subset of S. Hence, for λ ∈SD, we have The set D belongs to σ(TH++Kc) and it consists of isolated eigenvalues of finite algebraic multiplicity of TH++Kc. Now, we suppose that λ0∈σas(TH++Kc)≠0, and put λ1=Reλ0>s(TH+). So,there existsuch that F(λ0)ψ = ψ and then |ψ| ≤F(λ1)|ψ|. By the positivity of F(λ1)and [21, Theorem 7.3], we get Using Lemma 3.8, together with Equations (3.6) and (3.7), we infer that there exists λ∗∈(s(TH+),+∞) such that rσ(F(λ∗)) = 1. Furthermore, for all λ ∈(s(TH+),+∞), the operator F(λ) is positive and power compact(cf. Proposition 3.5),so,using the Krein-Rutman theorem (see, [24, Theorem 4.1.4], we deduce that rσ(F(λ)) is a eigenvalue of F(λ). Thus,there existsuch thatSo, because for all λ > λ∗,rσ(F(λ))<1, we conclude that λ∗is a real leading eigenvalue of TH++Kc. Proposition 3.11If the assumptions of Theorem 3.10 hold true, then ProofBy analyticity arguments, it suffices to restrict ourselves to the set σ(TH++Kc)We know, from the proof of Theorem 3.10, that the leading eigenvalue λ∗is characterized by the following equation We note that in the space L1(Ω×V,dxdµ(v)), there exists an alternative definition for the concept of regular collision operators. We first recall the definition of collectively weakly compact families of bounded linear operators between two normed spaces. Definition 3.12Let X and Y be two normed spaces and denote by B the closed unit ball of X. A set C of L(X,Y) is said to be collectively weakly compact, if and only if the set Now, we are in a position to define the notion of regular collision operators on L1(Ω ×V,dxdµ(v)) (see, for exemple, [25, 26]). Definition 3.13We say that Kcis a regular operator onif,for almost all x ∈Ω, the operator is weakly compact in L1(V,dµ(v)) and the family of such operator on L1(V,dµ(v)) indexed by x ∈Ω is collectively weakly compact. We introduce the following hypotheses required below: (A2) The measure dµ satisfies the following geometrical property for every c1< c2< ∞and c3< ∞, where |A| is the Lebesgue measure of A and χAdenotes the characteristic function of A. (A3) H is weakly compact. We recall the following result obtained in [13]. Lemma 3.14Let Ω be a convex bounded subset of RN. Assume that Kcis a regular collision operator and the hypotheses (A2) and (A3) hold true. Then, the operator Kc(λ −TH)−1Kcis weakly compact on L1(Ω×V,dxdµ(v)). As in the previous subsection, we set Proposition 3.15Let Ω be a convex bounded subset of RNand let λ ∈S. If the conditions (A2) and (A3) are satisfied and Kcis a regular collision operator, then is weakly compact on L1(Ω×V,dxdµ(v)). ProofFor any λ belonging to S, one has Because of Lemma 3.14,it suffices to establish that Ke(λ−TH)−1Kcand Kd(λ−TH)−1Kcare weakly compacts. We shall check the result for the operator Ke(λ −TH)−1Kc, and the proof for Kd(λ −TH)−1Kcfollows the same lines. To do so, the use of (2.5) gives We know from Theorem 5.3.1 in [7] that the operator Ke(λ −T)−1Kcis weakly compact on L1(Ω×V,dxdµ(v)), so it suffices to establish the weak compactness of the operator KeBλH(I −MλH)−1GλKc. This follows from the hypothesis (A3). Theorem 3.16Assume that the hypotheses of Proposition 3.15 hold true,then σas(TH++Kc)consists of, at most, isolated eigenvalues with finite algebraic multiplicities. Moreover,if, thenadmits a real leading eigenvalue ProofLet ψ ∈L1(Ω×V,dxdµ(v)), λ ∈C and we consider the problem where the unknown function ϕ must be sought in D(TH++Kc). As S ⊂ρ(TH+), we have Let F:S →L(L1(Ω×V,dxdµ(v))) be the operator valued function defined on S by Hence, for λ0∈S such that Re λ0is large enough, the operatoris invertible. According to the Gohberg-Smulyan theorem, the operatoris invertible for all λ ∈S except for a countable subset D of S. Furthermore, using the equality we infer that for all λ ∈SD, the operator(I −F(λ))is invertible, and its inverse is given by Hence, the solution of equation (3.9) is given by The set D belongs to σ(TH++Kc)and consists in isolated eigenvalues of finite algebraic multiplicity of TH++Kc. Remark 3.17The result of Proposition 3.11 is also valid for p=1. In this section we shall give some complementary results concerning the behavior of the leading eigenvalue in connection with positivity. The first part of this section is devoted to the irreducibility of(the C0-semigroup generated by the transport operator TH+Kc+). Recall that a positive C0-semigroupon a Banach lattice X is called irreducible if there is-invariant closed ideal except {0} and X (see, for example,[28] or [24] for the irreducibility of positive linear operators between Banach lattices). In fact,the interest of the irreducibility lies in the fact that ifis irreducible, then the leading eigenvalue (if it exists) is strictly dominant with multiplicity 1 and the associated eigen-function is strictly positive. So, this provides a simple description of the time asymptotic behavior (t →+∞) of the solution to the Cauchy problem governed by the transport operator TH+Kc+. The second part of this section will be concerned with the strict monotonicity of the leading eigenvalue with respect to the parameters of the transport operator such as the boundary operators and the collision ones. In order to speak about the concept of irreducibility or to discuss the strict monotonicity of leading eigenvalue, we need the following hypothesis: (A4) the operators H, Kcandare positive in the lattice sense. Note that, in neutron transport theory, this hypothesis is natural and not restrictive. Before going further, we first recall some estates required in the sequel. Let us remember that the resolvent operator of THis given by (cf. (2.5)) for each λ satisfying Reλ>−. It should be noticed that if H is positive (in the lattice sense) 0 ≤H (which is a natural hypothesis), then, according to Remark 2.3, we have (see Remark 3.3 in [13]) On the other hand, for each, we have Furthermore, it is clear that ifand, then Now, using (4.2) together with (4.3), we derive the estimate Note that it is well known that the operator TH+ Kcgenerates a strongly continuous semigroup(VH,Kc(t))t≥0onwith 1 ≤p<+∞(see,for example,[4, 13,14]and the references therein). The objective of this subsection is to complete this work by extending some of their results concerning the irreducibility of the transport semigroup to abstract boundary conditions in bounded geometry in the case where the collision operator involves further elastic and inelastic collision operators. More precisely, we shall discuss the influence of the boundary operators on the irreducibility of the semigroup generated by TH+Kc+on Lp(Ω×V,dxdµ(v))with 1 ≤p<+∞. Let S be an open subset of Rm, m ≥1, (S,Σ,µ) be a measure space, and Lp(S,dµ),1 ≤p<∞, be the Banach space of equivalence classes of measurable functions on S whose p’th power is integrable. Its dual space is Lq(S,dµ) where. The positive coneof Lp(S,dµ) is given by The set of strictly positive elements in Lp(S,dµ) is denoted by Definition 4.1Let S be a subset of Rn,(S,Σ,µ)be a measure space,and B be a positive linear operator from Lp(S,dµ)into itself. We say that B is strictly positive iffor all For our own use, we recall the following result in the context of Lp-spaces which is valid for general Banach lattices (see, for example, [28, p. 306]). Proposition 4.2Let (T(t))t≥0be a positive C0-semigroup on Lp(S,dµ) with generator A. Then, the following assertions are equivalent: (a) (T(t))t≥0is irreducible; (b) (λ −A)−1is strictly positive for some (every) λ>s(A). In the following,we shall denote by(VH,K(t))t≥0the semigroup generated by TH+Kc+,where K :=Kc+. Moreover,as TH+Kc+is the generator of C0-semigroup(VH,K(t))t≥0(use the fact that TH+Kc+is a bounded perturbation of TH+Kctogether with Phillips’s perturbation theorem, see, for example, [29]). Now, we are in a position to state and prove the following result. Theorem 4.3Assume that the hypothesis (A4) holds true. If one of the semigroups(VH,0(t))t≥0and (VH,Kc(t))t≥0is irreducible, then (VH,K(t))t≥0is irreducible. ProofIf(VH,0(t))t≥0is irreducible,then by Proposition 4.2,(λ−TH)−1is strictly positive for some (every) λ>s(TH+Kc+). So, using estimate (4.4), we infer that (λ −TH+Kc+)−1>0. Hence, the use again of Proposition 4.2 implies that the semigroup (VH,K(t))t≥0is irreducible. Assume now that (VH,Kc(t))t≥0is irreducible, then by Proposition 4.2, (λ −TH+Kc)−1is strictly positive for some (every) λ > s(TH+Kc+). As for the first case, the use of the estimate (4.4)implies that(λ −TH+Kc+)−1>0. Now,applying again Proposition 4.2,we get the desired result. It should be noticed that (VH,0(t))t≥0is nothing else but the semigroup generated by the operator TH. It is established in [21] that the irreducibility of (VH,0(t))t≥0implies that of the semigroup (VH,Kc(t))t≥0. However, the fact that (λ −TH+Kc)−1> 0 does not implies that(λ −TH)−1is strictly positive (use 4.2). So, the irreducibility of the semigroup (VH,Kc(t))t≥0does not implies that of (VH,0(t))t≥0. As it is seen above, the irreducibility of the semigroup (VH,0(t))t≥0implies that of(VH,K(t))t≥0(cf. Theorem 4.3). In the following two corollaries, we shall derive some sufficient conditions in terms of the boundary H guaranteeing the irreducibility of (VH,0(t))t≥0. Corollary 4.4Assume that the hypothesis (A4)holds true. If H(I −MλH)−1is strictly positive, then the semigroup (VH,K(t))t≥0is irreducible. ProofAccording to (4.1) and the positivity of Gλ, we have the estimate We note that the operators Gλis a strictly positive operator from Lp(Ω×V,dxdµ(v)) intoand Bλis a multiplication operator by a strictly positive function on Ω×V. Hence,(λ−TH)−1is a strictly positive operator on Lp(Ω×V,dxdµ(v)). Now the use of estimate(4.4)implies that(λ −TH−Kc−)−1>0. Now, the use of Proposition 4.2 ends the proof. Corollary 4.5Assume that the hypothesis (A4) holds true. If further<1, then he semigroup (VH,K(t))t≥0is irreducible if one of the following two conditions is satisfied: (a) H is strictly positive; (b) there exists an integer n0≥0 such that (MλH)n0is strictly positive. ProofAs(cf. Section 2), we haveand therefore MλH(I −. On the other hand,.So,because of the positivity of the operator MλH, we have MλH(I −MλH)−1≥(MλH)nfor all n ∈N∗.Thus, if one of two conditions (a) or (b) is satisfied, then the result follows immediately from(4.5), (4.4), and Proposition 4.2. In this subsection, we shall discuss the strict growth properties of the leading eigenvalue of AH=TH+Kc+with respect to the parameters H and Kc. Our analysis will be performed in the same way as in the works[3, 21] and uses positivity arguments [24] together with Theorem 2.8. Evidently, we suppose here that our operators satisfy the condition (A4). Let us first suppose that H1and H2are two boundary operators satisfying (A5) 0 ≤H1≤H2with It is clear that under the hypothesis (A5), we have In the following, we shall denote by λ(H) the leading eigenvalue of the operator AH(when it exists). Theorem 4.6Let p ∈(1,+∞) (resp. p=1) and assume that the conditions (A1) (resp.(A2)) and (A5) hold true. If Kcis a regular collision operator on Lp(Ω ×V,dxdµ(v)) and λ(H1) exists, then λ(H2) exists and λ(H1)≤λ(H2). Moreover,if (λ(H1)−TH2−)−1Kchas a strictly positive power, then λ(H1)<λ(H2). ProofLet us first note that, as Kcis regular, Proposition 3.5 implies that the operator(λ −TH1−)−1Kcis power compact operators on Lp(Ω × V,dxdµ(v)) with 1 ≤p < ∞.Applying the Krein-Rutman theorem,we see that λ(H1),the leading eigenvalue of TH1++Kc,is characterized by Because the operator (λ(H1)−TH2−)−1Kchas a strictly positive power, using Equations(4.6)–(4.7) together with Theorem 2.8, we conclude that This show that λ′=λ(H2) (the leading eigenvalue of the operator AH2), which completes the proof. Remark 4.7Let us observe that Hence, if there exists an integer m ≥1 such that Corollary 4.8Assume that the conditions (A1) (resp. (A2)) and (A5) are satisfied and Kcis regular collision operator on Lp(Ω×V,dxdµ(v)) and λ(H1) exists, then λ(H2)exists and λ(H1)≤λ(H2). Furthermore,if one of the following conditions is satisfied,then λ(H1)<λ(H2). (a) H2is strictly positive and ker(Kc)∩{ϕ ∈Lp(Ω×V,dxdµ(v)),ϕ ≥0}={0}; (b) There exists m ∈N∗such thatis strictly positive and ProofEvidently, as we have seen in the subsection above, if H2is strictly positive, thenis strictly positive, and sois strictly positive (use Equation(4.4)and take Kc=0). Now, as ker(Kc)∩{ϕ ∈Lp(Ω×V,dxdµ(v)),ϕ ≥0}={0},we conclude that the operator (λ(H1)−TH2−)−1Kcis also strictly positive and therefore λ(H1)<λ(H2). As it is seen in Remark 4.7,under the hypothesis(b),the operator(λ(H1)−TH2−)−1Kcis strictly positive. Using again the hypothesis kerwe conclude that the operator(λ(H1)−TH2−)−1Kcis also strictly positive, which conclude the proof. Let us now keep the boundary operator H fixed and focus our attention on the variation of the operator Kc. To this end, consider two operatorsandsatisfying In this case,we denote by λ(Kc)the leading eigenvalue of the operator AH=TH++Kc(when it exists). Noticing that for any realwe have the following estimate Theorem 4.9Let p ∈(1,+∞) (resp. p=1) and assume that the conditions (A1) (resp.(A2)) and (A6) hold true. Suppose further thatandare regular collision operators on Lp(Ω×V,dxdµ(v)) and λ() exists. Then, λ() exists and we have λ() ≤λ().Moreover, ifhas a strictly positive power, then λ()<λ(). ProofWe proceed as in the proof of Theorem 4.6. Asis regular, Proposition 3.5 implies that the operator(λ−TH1−)−1is power compact operators on Lp(Ω×V,dxdµ(v))with 1 ≤p < ∞. Applying the Krein-Rutman theorem, we see that λ(), the leading eigenvalue of TH++, is characterized by Remark 4.10For any regular collision operator Kc, we have the estimate The above equation shows that if (λ −TH)−1is strictly positive, then (λ −TH−−Kc)−1is strictly positive too. In the following corollary, we shall derive some sufficient conditions in terms of the boundary H guaranteeing the strict positivity of (λ −TH−−Kc)−1. Corollary 4.11Assume that the hypotheses (A1) (resp. (A2)) and (A6) hold true and Suppose further thatandare regular collision operators. If λ() exists, then λ()exists and we have λ()≤λ(c). Furthermore, assume that one of the following conditions is satisfied: (a) H is strictly positive and ker()∩{ϕ ∈Lp(Ω×V,dxdµ(v)),ϕ ≥0}={0}; (b) There exists an integer n0≥1 such that(Mλ(K1c)H)n0is strictly positive and ker()∩{ϕ ∈Lp(Ω×V,dxdµ(v)),ϕ ≥0}={0}.


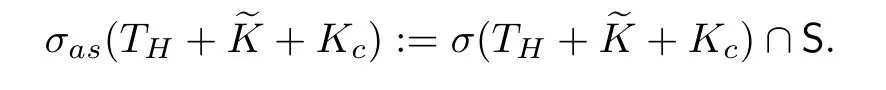




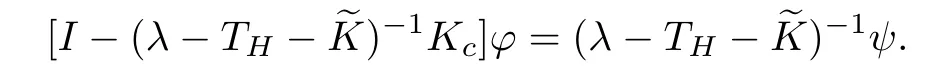










3.2 Case p=1
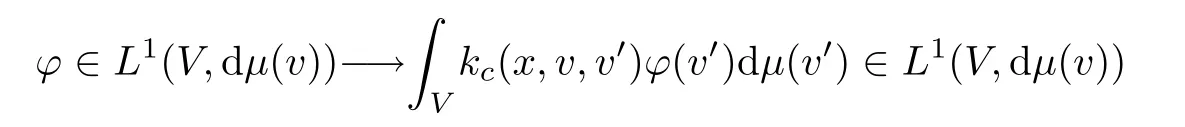

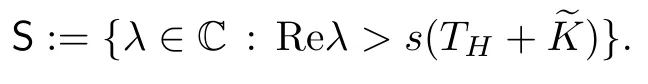
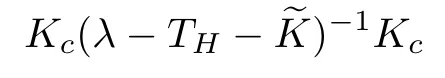






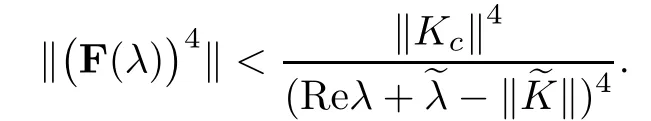





4 Some Remarks on the Leading Eigenvalue


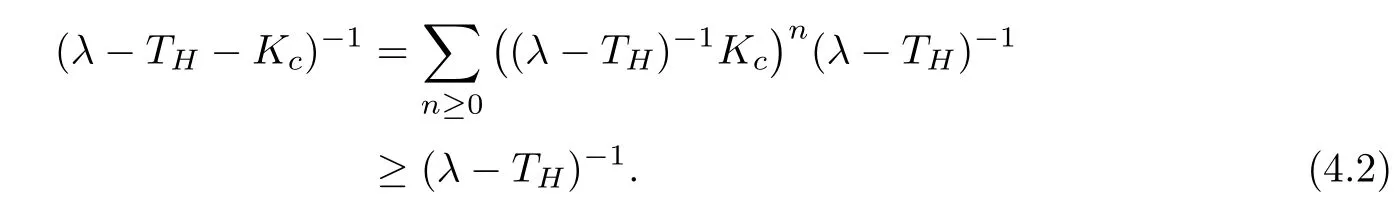


4.1 Irreducibility of the semigroup




4.2 Strict monotonicity of the leading eigenvalue

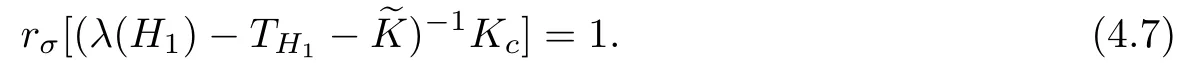
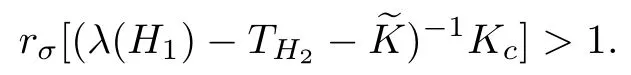


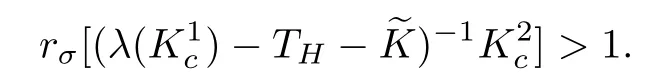


杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- ARTIAL REGULARITY FOR STATIONARY NAVIER-STOKES SYSTEMS BY THE METHOD OF A-HARMONIC APPROXIMATION*
- ON BLOW-UP PHENOMENON OF THE SOLUTION TO SOME WAVE-HARTREE EQUATION IN d ≥ 5*
- THE QUASI-BOUNDARY VALUE METHOD FOR IDENTIFYING THE INITIAL VALUE OF THE SPACE-TIME FRACTIONAL DIFFUSION EQUATION ∗
- ON APPROXIMATE EFFICIENCY FOR NONSMOOTH ROBUST VECTOR OPTIMIZATION PROBLEMS∗
- SYNCHRONIZATION OF SINGULAR MARKOVIAN JUMPING NEUTRAL COMPLEX DYNAMICAL NETWORKS WITH TIME-VARYING DELAYS VIA PINNING CONTROL∗
- ON THE ENTROPY OF FLOWS WITH REPARAMETRIZED GLUING ORBIT PROPERTY*
