ON THE ENTROPY OF FLOWS WITH REPARAMETRIZED GLUING ORBIT PROPERTY*

Peng SUN (孙鹏)

China Economics and Management Academy, Central University of Finance and Economics,Beijing 100081, China

E-mail: sunpeng@cufe.edu.cn

Abstract We show that a flow or a semiflow with a weak form of reparametrized gluing orbit property has positive topological entropy if it is not minimal.

Key words Flow; gluing orbit property; reparametrization; minimality; topological entropy

1 Introduction

The gluing orbit property introduced in [1–3] is a much weaker variation of the well studied specification property. It is satisfied by a larger class of systems while still implying interesting facts, as indicated by a series of recent works. See [4–9]. It is well known that specification property implies positive topological entropy. On the contrary, there are systems that have both gluing orbit property and zero topological entropy (for example, minimal translations on tori [4]). It seems that such systems should be quite simple. In [10], in the setting without reparametrizations, we showed that they must be minimal. In communication with Paulo Varandas, we realize that this result should be more practical for flows if reparametrizations can be allowed. In this article, we introduce an even weaker form of the reparametrized gluing orbit property defined in [4, 5]. We are able to extend our result to this case.

Theorem 1.1Let (X, ft) be a flow or a semiflow with weak reparametrized gluing orbit property. If (X, ft) is not minimal, then it has positive topological entropy.

The original motivation to study specification and gluing orbit properties was to understand the behavior of hyperbolic systems. In the smooth setting, positive topological entropy implies existence of nonzero Lyapunov exponents for some invariant measures. Theorem 1.1 indicates that in the non-minimal case, weak reparametrized gluing orbit property is still related to some weak form of hyperbolicity.

In [11], we obtain a complete description of systems with gluing orbit property and zero entropy: they are minimal and equicontinuous, hence they are conjugate to minimal rotations on compact abelian groups. It is still an open question whether zero-entropy semiflows with (weak) reparametrized gluing orbit property are equicontinuous. Moreover, we have a work inprogress whose result implies that a minimal semiflow with reparametrized gluing orbit property must have zero topological entropy. We also have a similar result [12] on zero-entropy systems satisfying properties that are even weaker than gluing orbit.

Preliminaries and definitions will be provided in Section 2. Then, we prove Theorem 1.1 in Section 3.

2 Preliminaries

Let (X,d) be a compact metric space. Let f : D×X →X be a continuous function such that

Then, the pair (X,ft), where ft(x)=f(t,x), is called a flow on X if D =R, or a semiflow on X if D =[0,∞).

Definition 2.1A strictly increasing continuous function γ : [0,∞) →[0,∞) satisfying γ(0) = 0 is called a reparametrization. For L ≥1, a reparametrization γ is called an Lreparametrization if

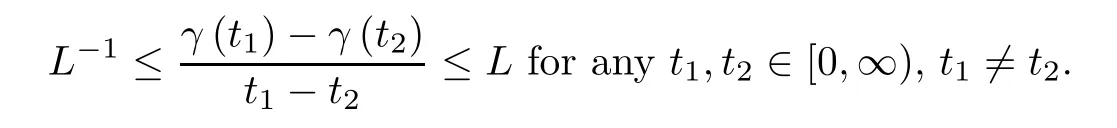
Note that a 1-reparametrization is just the identity map Id(x)=x on [0,∞).

Definition 2.2We call the finite sequence of ordered pairs

an orbit sequence of rank k. A gap for an orbit sequence of rank k is a (k −1)-tuple

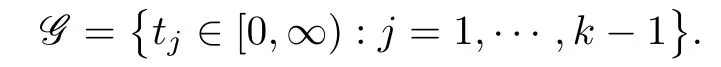
Let (X,ft) be a flow or a semiflow, and γ be a reparametrization. For ε > 0, we say that(,γ) is ε-traced by z ∈X if for every j =1,··· ,k,

where

Definition 2.3We say that (X,ft) has specification property if for every ε>0, there is M(ε)>0, such that for any orbit sequenceand any gapwith min≥M(ε), (,Id)can be ε-traced by some z ∈X.

For detailed discussion on specification property, the readers are referred to [13–15].

Definition 2.4We say that (X,ft) has gluing orbit property if for every ε>0, there is M(ε)>0, such that for any orbit sequence, there is a gapwith max≤M(ε), such that(,Id) can be ε-traced by some z ∈X.

Definition 2.5We say that(X,ft) has reparametrized gluing orbit property if for every ε>0, there is M(ε)>1, such that for any orbit sequence, there are a gapwith max≤M(ε) and a (1+ε)-reparametrization γ such that (,γ) can be ε-traced by some z ∈X.

The gluing orbit property in Definition 2.4 has been discussed in [10]. Definition 2.5 is equivalent to the definition of reparametrized gluing orbit property introduced in[5]. In Definition 2.5, a reparametrization that tends to identity as ε goes to 0 is allowed. We perceive that our result only requires an even weaker condition, where the reparametrization can be more flexible when ε gets smaller.

Definition 2.6We say that (X,ft) has weak reparametrized gluing orbit property if for every ε > 0, there is M = M(ε) ≥1, such that for any orbit sequence, there are a gapwith max≤M and an M-reparametrization γ such that (,γ) can be ε-traced by some z ∈X.

It is clear that reparametrized gluing implies weak reparametrized gluing. Note that in Definition 2.6, we combine the bounds for the gap and for the reparametrization as a single M(ε) for convenience. The definition remains equivalent if they have different bounds.

By[4],a minimal translation has gluing orbit property. Moreover,the product of a flow with gluing orbit property and a flow with specification property has gluing orbit property. After a bi-Lipschitz time change, a flow with gluing orbit property preserves weak reparametrized gluing orbit property. Weak reparametrized gluing orbit property is a topological invariant and is preserved under topological conjugacy. More examples with reparametrized gluing orbit property can be found in [3, 4].

For completeness, we recall the definition of topological entropy for flows(see,for example,[16]) and the definition of minimality.

Definition 2.7Let(X,ft)be a flow or a semiflow. For T >0 and ε>0,a subset E ⊂X is called an(T,ε)-separated set for(X,ft)if for any distinct points x,y in E,there is τ ∈[0,T]such that

Denote by s(T,ε)the maximal cardinality of(T,ε)-separated subsets of X. Then the topological entropy of (X,ft) is defined as

Definition 2.8Let (X,ft) be a flow or a semiflow. We say that (X,ft) is minimal if for every x ∈X, the forward orbitis a dense subset of X.

3 Proof of the Theorem

Throughout this section, we assume that (X,ft) is a flow or a semiflow that has weak reparametrized gluing orbit property and that is not minimal. We shall show that the topological entropy h(ft)>0.

Lemma 3.1There are z ∈X, ε>0, and τ >0 such that d(ft(z),z)≥ε for any t ≥τ.

ProofAs(X,ft)is not minimal,there is a point x ∈X whose forward orbit is not dense.

Hence, there is y ∈X and δ >0 such that d(ft(x),y)≥δ for any t ≥0.

As (X,f) has weak reparametrized gluing orbit property, there are zn∈X, τn∈[0,M], and an M-reparametrization γn, such thatis ε-traced by zn. Then, for any t ≥M2and n ≥Mt, we have

Hence, by (2.1), for any t ≥M2and n ≥Mt, we have

and

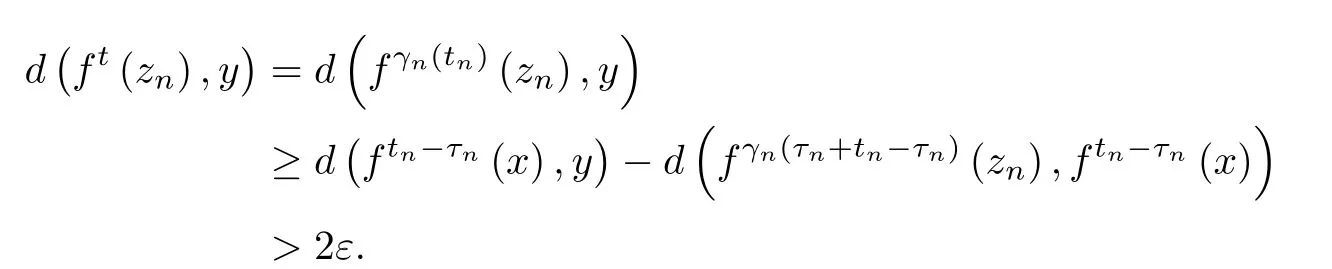
Let z be a subsequential limit of. Then

Note that by (3.1),

So, by (3.2) and (3.3), for τ :=M2we have

Lemma 3.2There are x,y ∈X, ε>0, and T >0, such that

ProofBy Lemma 3.1, there are x ∈X, ε0>0, and τ >0, such that

Let ε1:=and M :=M(ε1)>1 as in Definition 2.6. As(X,f)has weak reparametrized gluing orbit property,for each n ∈Z+,there are yn∈X,τn∈[0,M]and an M-reparametrization γnsuch thatis ε1-traced by yn. Let

For any t ≥T and n ≥Mt, we have

and tn−τn>τ. Hence by (2.1), for any t ≥T and n ≥Mt, we have

and

As γnis an M-reparametrization, we have τ ≤γn(Mτ +τn)≤T for each n. Then, there are T0∈[τ,T] and a subsequencesuch that

Let y be a subsequential limit of {ynk}. Then by (3.5), we have

By (3.4), (3.7), and (3.8), we have for any t ≥T:

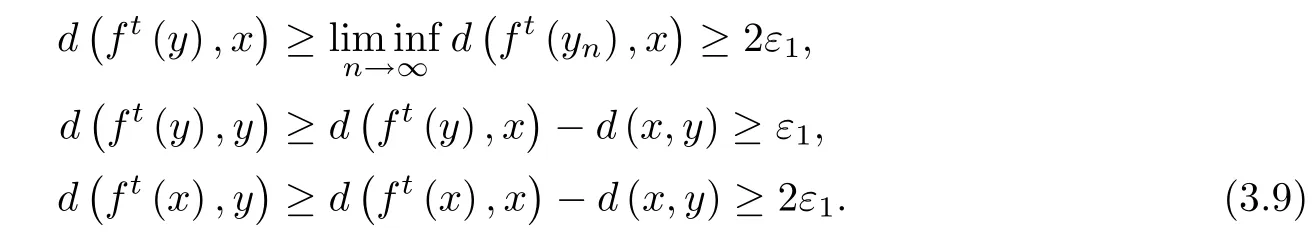
Note that by (3.4) and (3.6), for any t ≥0, we have

Then, 0<ε ≤ε1. By (3.9) and (3.10), we have

The lemma holds for x, y, ε, and T.

Proposition 3.3(X,ft) has positive topological entropy.

ProofLet x,y ∈X, ε > 0 and T > 0 be as in Lemma 3.2. Let 0 < ε01 as in Definition 2.6. Denote

Consider the orbit sequences

Let n ∈Z+. For each, define

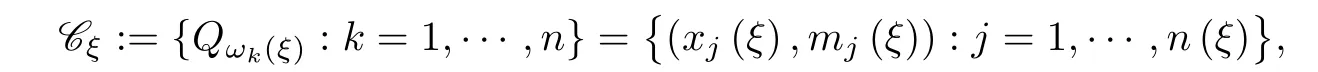
Let

Then for each ξ ∈{1,2}n, we have sn(ξ)(ξ)

and

For each j ≤l, denote

We remark that the discussion of rjin (3.11) is essential in the proof of Theorem 1.1, which solves the most extra difficulty caused by reparametrization. Our discussion can be divided into the following cases.

Case 1l=1

We may assume that x1(ξ)=x and x1(ξ′)=y. Then by Lemma 3.2, we have

In this case, we can take s=0.

Case 2l ≥2 and rl≥T.

Denote

As r1=0, we have k ≥2 and hence rk−1γξ′(sk(ξ′)).

Subcase 2.1

Note that

There is r ∈(T,mk−1(ξ′)], such that

Then by Lemma 3.2, we have

In this subcase, we can take s=γξ(sk(ξ)).

Subcase 2.2γξ(sk(ξ))>γξ′(sk−1(ξ′)+mk−1(ξ′)).

In this subcase, we have

Then by Lemma 3.2, the fact that rk∈[T,T2) implies that

In this subcase, we can take s=γξ′(sk(ξ′)).

Case 3l ≥2 and rl

We may assume that xl(ξ)=y and xl(ξ′)=x.

Subcase 3.1γξ′(sl(ξ′))≤γξ(sl(ξ)).

Note that rl

In this subcase, we can take s=γξ(sl(ξ)).

Subcase 3.2

Note that by the definitions of Cξand Cξ′, we must have

Then in this subcase, we have

and

So, there is r ∈(T,T1], such that

By Lemma 3.2, we have

In this subcase, we can take s=γξ′(sl+1(ξ′)).

The above argument shows that E :=�zξ:ξ ∈{1,2}n�is an (nMT3,ε0)-separated subset of X that contains 2npoints. Hence

AcknowledgementsThe author would like to thank Paulo Varandas, Xueting Tian,and the anonymous referees for their helpful comments and suggestions.