A BLOW-UP CRITERION OF STRONG SOLUTIONS TO THE QUANTUM HYDRODYNAMIC MODEL*

Guangwu WANG (王光武) †

School of Mathematics and Information Science, Guangzhou University, Guangzhou 510006, China

E-mail: yunxianwgw@163.com

Boling GUO (郭柏灵)

Institute of Applied Physics and Computational Mathematics, China Academy of Engineering Physics,Beijing 100088, China

E-mail: gbl@iapcm.ac.cn

Abstract In this article, we focus on the short time strong solution to a compressible quantum hydrodynamic model. We establish a blow-up criterion about the solutions of thecompressible quantum hydrodynamic model in terms of the gradient of the velocity, the second spacial derivative of the square root of the density, and the first order time derivative and first order spacial derivative of the square root of the density.

Key words Compressible quantumhydrodynamic model; blow-up criterion; strong solution

1 Introduction

In this article, we will investigate the blow-up criterion of the quantum hydrodynamic model(QHD):

Here, ρ and u represent the density and the velocity of the fluid. And P(ρ)is the pressure. We choose the isentropic case for simplicity, for example: P(ρ) = ργ(γ > 1). The parameter ε is the scaled Planck constant. u ⊗u denotes the matrix with element uiuj(i,j =1,··· ,n). Andis the quantum Bohm potential.

In this article, we will consider that the initial data to equation (1.1)–(1.2) are

Here, Ω is the sub-domain of Rn. When we consider the boundary value problem, we can assume that the boundary conditions satisfy that

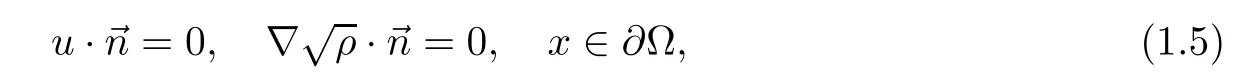
This model (1.1)–(1.2) was firstly derived by Madelung [28] in 1927 from the Schrödinger equation for the wave function ψ:

by the so-called Madelung transformation

Here, n ≥1, ε>0 is the scaled Planck constant, and h is an integrable function such that

ρ=|ψ|2is particle density, and S is a phase function.

The Schrödinger equation (1.6) can be used to describe multi-particle approximations in the mean field theory of quantum mechanics, when one considers a large number of quantum particles acting in unison and takes into account only a finite number of particle-particle interactions.

Next, we will give a brief derivation from the Schrödinger equation to the quantum hydrodynamic model. Indeed, from (1.8), we obtain that

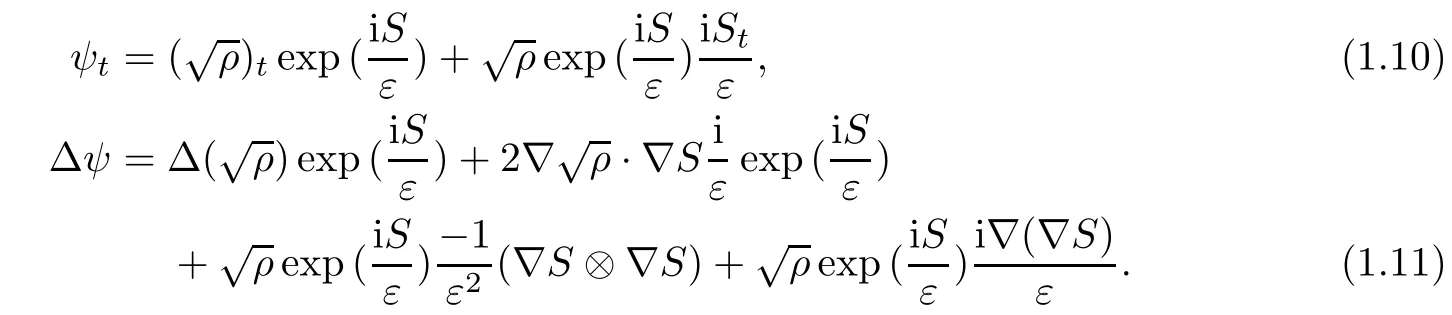
Then, by plugging (1.10) and (1.11) into (1.6), the imaginary and real parts of the resulting equation are

Then, setting u = ∇S, we can formally get the compressible quantum hydrodynamic model(1.1)–(1.2).

The formal equivalence between (1.1)–(1.4) and (1.6)–(1.7) is explained more in details in the following lemma.

Lemma 1.1Let ψ be a solution to (1.6)–(1.7) with initial datumthe functions ρ := |ψ|2andsolve (1.1)–(1.4) with initial data ρ0= |ψ0|2and u0=∇S0as long as ρ>0.

Vice versa, let (ρ,u) be a solution to (1.1)–(1.4), where u = ∇S and ρ > 0 in Rd, t > 0;the functionsolves (1.6)–(1.7).

The system(1.1)–(1.2)can be interpreted as the compressible Euler equations coupled with the quantum Bohm potential. It is used for the modeling of superfluid phenomena like Helium II [24, 25, 27]. They also can be described by a dispersive perturbation associated to the Hamilton-Jacobi system for compressible fluid dynamics,sometimes referred as a dispersive perturbation of the Eikonal equation for the evolution of amplitude and phase velocity of quantum wave guides. This system(1.10)–(1.11)can be also used to describe the Bose-Einstein condensation in trapped gases [5].

Next,we provide another compressible quantum hydrodynamic model,which is also called,the compressible quantum Euler-Poisson equation. Gardner [9] and Gasser et al. [10, 11]derived the compressible quantum Euler-Poisson equations which include an exterior electric field and a momentum relaxation term taking into account interactions of the electrons in the semiconductor crystal, and are self-consistently coupled to the Poisson equation for the electrostatic potential:

Remark 1.2The system(1.14)–(1.16)are referred as the quantum Euler-Poisson system or as the quantum hydrodynamic model. It is not difficult to find that (1.11) and (1.15) are different from the last two term: the exterior electric fieldand the relaxation term.

There are a large amount of the results about the quantum Euler-Poisson equation(1.14)–(1.16). In 1998,A.Jungel[20]proved the existence of the sub-sonic steady solution to equation(1.14)–(1.16) with Dirichlet boundary condition in Rn(n ≥1). In 2006, F.M. Huang, H.L. Li,and A. Matsumura [15] obtained the existence, uniqueness, and long time exponential stability of the sub-sonic steady-state solution in R1. The other results about the existence of the subsonic steady state solution with different boundary conditions were given by S.Nishibata and M.Suzuki[29, 30], A. Jungel and H.L. Li [21], B.Zhang and J.W.Jerome[32]. In[22],J¨ungel and J. Li proved that if the initial data are close enough to the steady-state solution, the local-intime solutions will exist globally in time (so-called small solutions). The local-in-time existence of the solutions for equations (1.14)–(1.16) in the multi-dimensional torus for the irrotational velocity was investigated by Li and Marcati in [26], and they also proved that local-in-time solutions exit globally and converge toward the corresponding steady-state as t →∞under a”subsonic”type stability condition. While for the rotational fluid, the local-in-time and globalin-time solutions of equations(1.14)–(1.16)in Rnwere also obtained by Huang,Li,Matsumura,and Odanaka in [16]. Here, we must emphasize that because of the existence of the relaxation term,we can easily show that the local-in-time solution is globally existing near the equilibrium state and exponentially decaying to the equilibrium state.

The existence of the global weak solutions of (1.14)–(1.16) with the finite energy in three dimension was proved by Antonelli and Marcati in [1]. In [2], Antonelli and Marcati given the finite energy weak solution of equations (1.1)–(1.2) with Poisson equation and (1.14)–(1.16) in two dimension. For the multi-dimensional case,Gasser and Markowich[10]proved the existence of the global finite energy weak solution to system (1.1)–(1.2) with a electric potential term.

In[7,8],Gamba and J¨ungel studied the positive steady-state solutions to the potential flow of (1.1)–(1.2). The existence of the solutions to one-dimensional stationary viscous quantum hydrodynamic model was proved in [12, 23].

In [6], Gamba, Gualdani, and Zhang proved that the smooth solution of (1.1)–(1.2) will blow-up in finite time for some boundary condition in a bounded domain. The main ideal of the proof in [6] is that the non-negative quantity I(t) will be negative if the smooth solution exists long enough. In [13], we prove the blow-up of the smooth solution to the initial value problem of the compressible quantum hydrodynamic model (1.1)–(1.2) in Rn. While for the initial boundary value problem of the compressible quantum hydrodynamic model (1.1)–(1.2)in the half space, the smooth solution will also blow up [14]. All the results about the blow-up time of the smooth solution is only dependent on the initial data and the boundary value. But we do not know the blow-up mechanism of the solutions, so in this article and the further work, we will give some blow-up mechanism of the strong solution to the compressible quantum hydrodynamic model (1.1)–(1.2).

Next, we will introduce some results about the blow-up criterion of the strong solution to the isentropic compressible Navier-Stokes equation. The earlier result about the blow-up criterion of the solution to the isentropic compressible Navier-Stokes equation was proved by Cho, Choe, and Kim [3]:

Later, X.D. Huang and Z.P. Xin[19] got a Beal-Kato-Majda type blow-up criterion about the isentropic compressible Navier-Stokes equation:

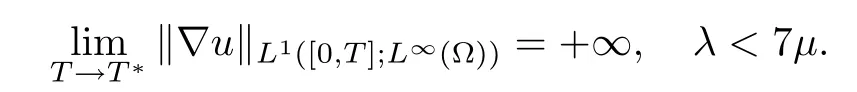
And Y.Z. Sun, C. Wang, and Z.F. Zhang[31] proved a similar Beal-Kato-Majda type blow-up criterion about the isentropic compressible Navier-Stokes equation:

In 2008, J.S. Fan and S. Jiang [4] obtained a new blow-up criterion of the strong solution to the compressible Navier-Stokes equation:

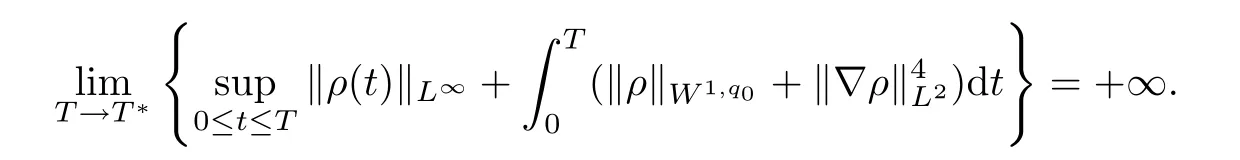
About the isentropic compressible Navier-Stokes equation, X.D. Huang, J. Li, and Z.P. Xin established the Serrin type blow-up criterion [18]:

and the Ponce type blow-up criterion [17]:

respectively.

Next, we will state the main results of this article about a blow-up criterion of the quantum hydrodynamic model.

Theorem 1.3Let Ω be a sub-domain of Rn. The initial data satisfy the following conditions:

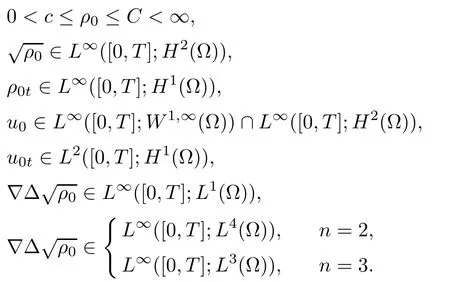
And the boundary condition (1.5) is satisfied if Ω has a boundary. Assume that (ρ,u) is a strong solution to equation (1.1)–(1.2) for t ∈[0,T), which satisfies

If T∗<+∞is the maximal time of existence, then

Because the moment equation in the compressible quantum hydrodynamic model (1.1)–(1.2) has a third order term of the density, it will bring a dispersive of the density, so we need at least a second order derivative estimate of the density. On the other hand, the estimate aboutcan ensure to obtain the second spatial estimate of the velocity.

The organization of this article is in the followings. In Section 2, we firstly give some notations which will be used in the next section. In Section 3, we will give the detailed proof of the main theorem 1.3. Here, we use the proof by contradiction. We assume equation (1.18)does not hold, then we prove that the strong solution will exist globally.

2 Preliminaries

NotationC always denotes generic positive constant. Ls(Ω), 1 ≤s ≤∞, is the space of s-powers integral functions on Ω with norm. Particularly,the norm of the space of square integral functions on Ω is denoted by. Hk(Ω)with integer k ≥1 denotes the usual Sobolev space of function f, satisfyingf ∈L2(0 ≤i ≤k), with normhere and after,for |α| = α1+α2+···+αdand ∂j= ∂xj, j = 1,2,···d, for abbreviation. Moreover,Wk,p,with k ≥1,p ≥1,denotes the space of functions with Dlf ∈Lp,0 ≤|l|≤k.

3 The Proof of the Main Results

In this section, we will use the contradiction method to prove Theorem 1.3. First of all,we assume that (ρ,u) is a strong solution to the quantum hydrodynamic equations(1.1)–(1.2),which also satisfies

Next, we have the basic energy estimate.

Lemma 3.1There holds that

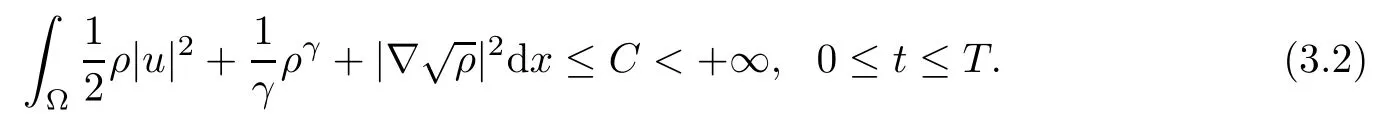
ProofMultiplying (1.2) by u, and integrating by parts, we get

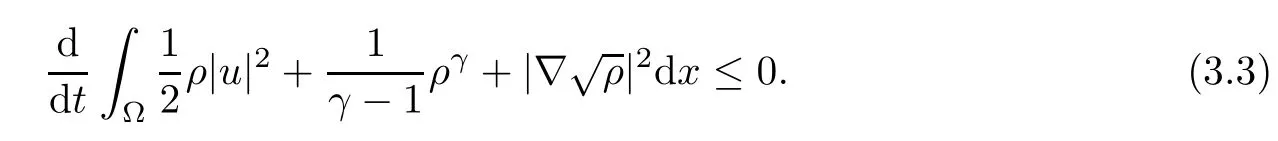
Here, we use the following facts:

Then, integrating inequality (3.3) on Ω, we can get inequality (3.2).

Lemma 3.2Assume that

then

ProofFrom the conversation equation of mass, we have for any r>1,

Integrate (3.6) over Ω to obtain

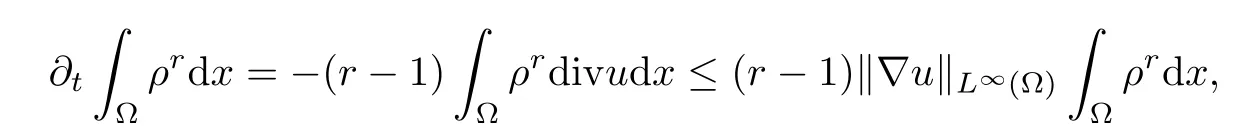
Next, we will derive the bound of

Lemma 3.3Under assumption (3.5), we have, for any r ≥2,

ProofMultiplying (1.2) by r|u|r−2u, and integrating by parts, we have the followings:

As the initial density satisfies

using the the proof of Lemma 3.2 and the fact that, we know

From the conversation of the mass, we get the equation about √ρ,∇√ρ:

Lemma 3.4Under assumption (3.1), we have the following estimate about utand

ProofFirstly, we can get the equation about the velocity u,

Multiplying equation (3.14) by utand integrating by parts, we get

As

we know

From equation (3.11), we know

On the other hand, we get the following estimates:

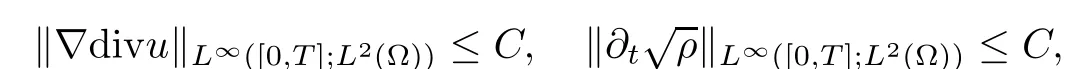
and

Therefore, we complete the proof of this lemma.

Lemma 3.5Under assumption (3.1), we have

and specially,

(1) n=2,

(2) n=3,

ProofIndeed, from the velocity equation (3.14), we have

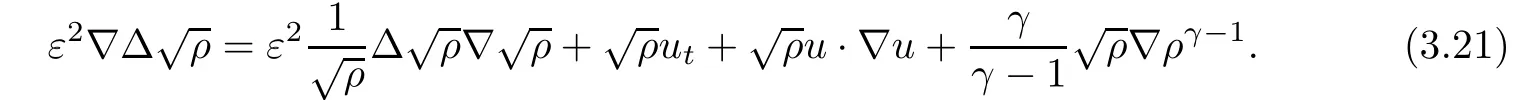
Thus, we obtain