A LIMIT LAW FOR FUNCTIONALS OF MULTIPLE INDEPENDENT FRACTIONAL BROWNIAN MOTIONS*
2020-08-02QianYU余迁
Qian YU (余迁)
School of Statistics, East China Normal University, Shanghai 200241, China
E-mail: qyumath@163.com
Abstract Let B = {BH(t)}t≥0 be a d-dimensional fractional Brownian motion with Hurst parameter H ∈ (0, 1). Consider the functionals of k independent d-dimensional fractional Brownian motions where the Hurst index H = k/d. Using the method of moments, we prove the limit law and extending a result by Xu [19] of the case k = 1. It can also be regarded as a fractional generalization of Biane [3] in the case of Brownian motion.
Key words Limit theorem; fractional Brownian motion; method of moments; chaining argument
1 Introduction
Let B = {BH(t)}t≥0be a fractional Brownian motion (fBm) with Hurst parameter H ∈(0,1). A stochastic calculus with respect to it has been intensively developed(see,for example,Biagini et al. [2], Nualart [9]). It is a central Gaussian process with BH(0) = 0 and the covariance function
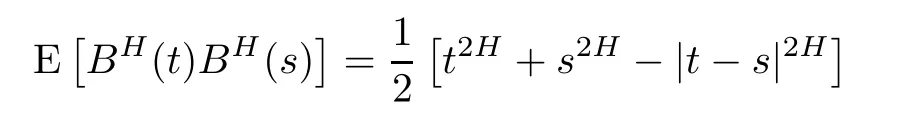
for all t,s≽0. This process was first introduced by Kolmogorov and studied by Mandelbrot and Van Ness [8], where a stochastic integral representation in terms of a standard Brownian motion was established:
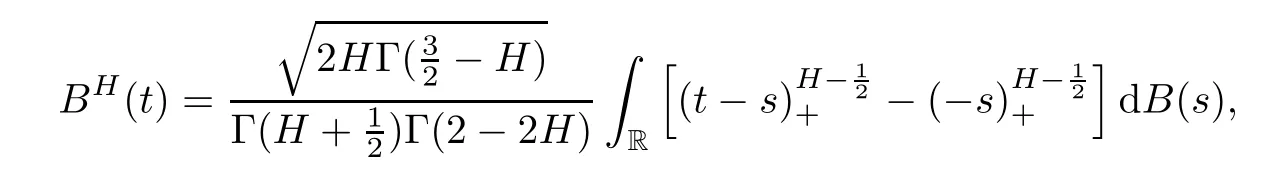
where u+=max{u,0},and B(s) is standard Brownian motion. For H =, BHcoincides with the standard Brownian motion B, but BHis neither a semimartingale nor a Markov process unless H =.
On the basis of sufficient study of fBm, the research technology of the fBm is gradually mature, and many results about Brownian motion can be extended to the fBm, especially some classical limit theories. In this article, we will consider the limit law for functionals of d-dimensional fBm. Let{BH(t)=(BH1(t),··· ,BHd(t)),t ≥0}be a d-dimensional fBm with Hurst index H in (0,1). Let BH,1, BH,2,··· ,BH,kbe k independent copies of BHwith H = k/d. If k = 1, the local time of fBm BHdoes not exist. This is called the critical case.In this condition, Xu [19] considered the limit law. That is, for any bounded and integrable function f : Rd→R and fRdf(x)dx=0,
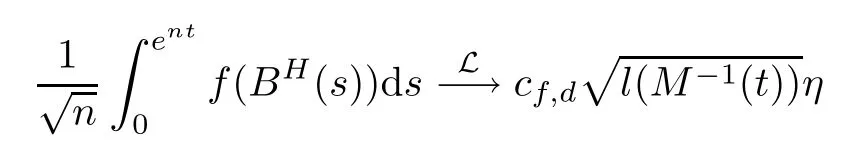
as n tends to infinity, where cf,dis a constant depend on f and d, l(t) is the local time at 0 of a Brownian motion B(t),and η ia a standard normal random variable independent on l(M−1(t)). In Biane[3], the limit law with conditionwas called the second order limit law, and whenwhich corresponded to the first order limit law. This extended the result of Kallianpur and Robbins [5], Kasahara and Kotani [6] in Brownian motion.
If k =2,the intersection local time of BH,1and BH,2does not exist. For Brownian motion,when H =and d=4,LeGall[7]proved the limit law for functionals of the difference between two independent Brown motions. Bi and Xu [1] generalized the limit theorem to fBms with d ≥4. Recently, Song, Xu, and Yu [16] considered the limit theorems for functionals of two independent Gaussian processes. When the Gaussian process take into fBm, the corresponding convergence in law is as follows:
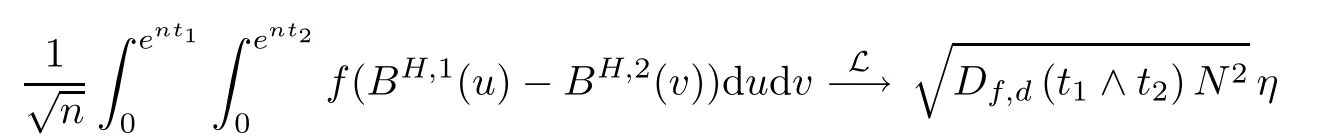
as n tends to infinity, where Df,dis a constant depend on f and d, and N and η are two independent real-valued standard normal random variable. This result can be understood as a supplement to the result of Bi and Xu [1] with d = 3 and H =, and extended the result to second-order limit law with H =.
For the condition k ≥3,Biane[3]has given the second-order convergence in law of Brownian motion. On this basis and drawing on the methods of Xu [19] and Song, Xu and Yu [16]at the same time, we deduce that the second-order limit theory of fBm can also be established under k ≥3.
To obtain more precise result, we will prove second-order limit law for fBm in this article,and next theorem is the main result.
Theorem 1.1Suppose that Hd=k and f is a bounded measurable function on Rdwithandfor some β >0. Then, for any t1, t2,··· ,tk≥0,
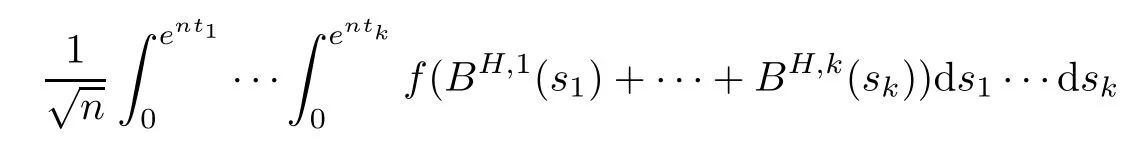
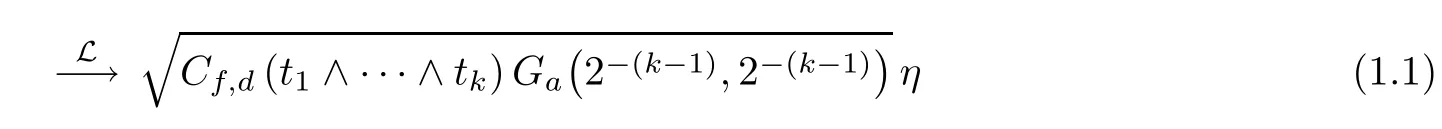
as n tends to infinity, where Gais a random variable of Gamma distribution, η ia a standard normal random variable independent on Ga, and

with B(·,·) being the Beta function and Γ(·) being the Gamma function.
Remark 1.2As the function f is bounded,we can always assume that β ≤1. Moreover,the assumption on f also implies that f ∈Lp(Rd) for any p ≥1. Note that
Example 1.3Let f(x) = −(2π)−d/2xe−x2/2and denoting pε(x) = (2πε)−d/2e−|x|2/(2ε),Theorem 1.1 provides that the exploding rate of derivative of local time for k independent fBms
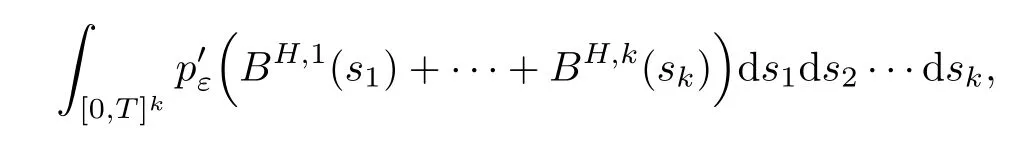

Limit theorems for functionals of multiple independent Brownian motions and their extensions were obtained in Biane [3] and references therein. However, the corresponding results for fBms were not much. As we all know, the general fBm with Hurst index not equal tois neither a Markov process nor a semimartingale. This means that the methods working for Brownian motions would probably not be used to prove Theorem 1.1 here.
To obtain Theorem 1.1, we would use the methods of moments and some kind of chaining argument, because these methods are becoming more and more mature for fBm. For example,Nualart and Xu [10] first use the chaining argument plus the methods of moments to prove the central limit theorem for an additive functional of the d-dimensional fBm with Hurst indexAfter that, Nualart and Xu [11] shown the central limit theorem for functionals of two independent fBm withLater,Bi,and Xu in[1]proved the first-order limit law in the critical case Hd = 2 with H ≤1/2. Recently, Xu [19] considered the second-order limit laws for additive functionals of d-dimensional fBm with H =.
From all above, we can see that the methods of moments and chaining argument are very powerful to prove the limit theorem for functionals of fBm, but for the convergence in law about k independent d-dimensional fBm still has the certain difficulty. The main difficulty is the computational complexity of multiple stochastic integral and the convergence of the corresponding even moments. Multiple stochastic integral with respect to fBm was studied in [4, 18]. Moreover, in this article, the related results can be extended to the cases of other Gaussian processes, for example, the case of sub-fBm, as the stochastic analysis about subfBm are very rich (see [14, 15, 17, 20]). At the same time, the corresponding conclusion of non-Gaussian processes (see [12, 13]) will be the direction of future research.
This article is outlined in the following way. After some preliminaries in Section 2, Section 3 is to prove the main result Theorem 1.1, on the basis of the method of moments and the Fourier transform. Throughout this article, if not mentioned otherwise, the letter c, with or without a subscript,denotes a generic positive finite constant whose exact value is independent of n and may change from line to line. Moreover, we use ι to denoteand x·y the usual inner product in Rd.
2 Preliminaries
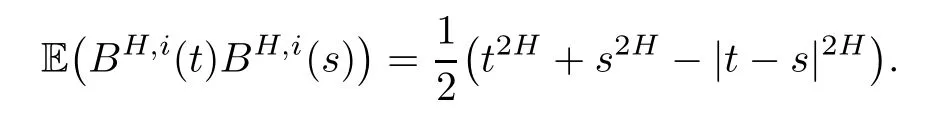
We shall use the following two properties of fBm BHto give our proof in next section. The first one is available in [11]. The second one gives estimates to the covariance of increments of fBm on intervals with uncomparable lengths and the key ingredient in the proof of Theorem 1.1, which are available in Lemma 2.4 of [16].
Lemma 2.1Given n ≥1, there exist two constants κHand βHdepending only on n, H,and d, such that for any 0=s0 The first inequality above is called the local nondeterminism property. Moreover, the inequalities in Lemma 2.1 can be rewritten as Lemma 2.2For any 0 < t1< t2< t3< t4< ∞and γ > 1, we have the following estimates: where ∆ti=ti−ti−1for i=2,3,4. In this section, we will give the proof of Theorem 1.1. For simplicity of notation, we use Fn(t1,··· ,tk) to denote the random variables on the left hand side of (1.1), and In order to obtain the limiting distribution of Fn(t1,··· ,tk), we start show that Fn(t1,··· ,tk)have the same limiting distribution as Fn(t)defined in(3.1)with t=t1∧···∧tkin Lemmas 3.4 and 3.5. Then, we prove that the m-th moment of Fn(t) is asymptotical equal todefined in(3.2) by Lemma 3.7. Finally, we obtain the convergence of corresponding moments in Proposition 3.8, which gives the desired result of Theorem 1.1. At first, to simplify the proofs of our main results, we give some lemmas as follows. Lemma 3.1For fixed t>0, we have ProofBy the ball coordinate transformation of multiple integral and for any a, b>0, Then, where in the equality, we use the fact that=d. Lemma 3.2For α>0, we have ProofIntegrating with respect to x gives where the proof of the last inequality is similar to that of Lemma 3.1. Lemma 3.3Letbe the Fourier transform of f, we have ProofUsing the change of variables si=|x|1/Hsifor i=1,2,··· ,k, where the last integral is finite by Remark 1.2. The following result shows that the limiting distribution of Fn(t1,··· ,tk) depends on t1∧···∧tk. Lemma 3.4For fixed ti→0,i=1,··· ,k, we have ProofWithout loss of generality, we assume that t1=min{t1,··· ,tk}, then, we have where we use the fact that the probability density function of BH,1(s1)+···+BH,k(sk) is less thanin the second inequality and make the change of variablesin the third inequality. Lemma 3.5Let Then, we have ProofIt is easy to find that then, by the boundedness and integrability of function f, we can obtain This completes the proof. Combining Lemma 3.4 with Lemma 3.5,we only need to consider the convergence of random variables In the following content, we will use the local nondeterminisim and the chaining argument properly to obtain the main estimates in Lemma 3.6, which is helpful in proving Lemma 3.7 and play a very important role in computingin Proposition 3.8. Let Applying the similar techniques as [16] and the local nondeterminism property in Lemma 2.1, we have Using the chaining argument introduced in [10], we have where In this way, we obtain the decomposition where The estimation of each term Al,mis given as follows. Lemma 3.6For any fixed positive constant λ < 1/2, there exists a positive constant c such that (i) Al,m≤c n−λfor l =1,2,··· ,m −1, (ii) Am,m≤if m is odd and Am,m≤c if m is even. ProofTo prove part (i), we first consider the case when k is odd. By the assumption on f, we can obtainfor any α ∈[0,β]. Then, Al,mis less than a constant multiple of Integrating with respect to the xis and sj(i) (for j =1,2,··· ,k) with i ≤l −1 gives By Lemmas 3.1 and 3.2, Choosing α small enough such that gives By the same way, we obtain the case when l is even. Choosing α small enough such that gives Combining (3.5) and (3.6) gives the desired estimates in part (i). Finally, we study part (ii). If m is odd, then, where the last second inequality follows from Lemma 3.3 and the last inequality follows easily from Remark 1.2. If m is even, then, by Lemma 3.3, This completes the proof. Lemma 3.7 ProofNotice that Applying Hölder inequality to the above integral on the term I2,2, we have Using the similar techniques, we obtain and Thus, we only need to consider the convergence of and From (3.2), (3.4), and Lemma 3.6, we have Using Fourier inverse transform, where Ufis the Fourier inverse ofand we use Lemmas 2.1 and 3.1 in the last inequality. From all above, we can find Hence, this completes the proof. From (3.2), applying Fourier transform, we can rewrite Proposition 3.8If m is odd, then,If m is even, then, ProofThe convergence of odd moments follows easily from Lemma 3.6. So,we only need to show that the convergence of even moments. Define where ∆uk=uk−uk−1for k =1,2,··· ,m with the convention u0=0. Let Then, by (3.3) and Lemma 3.6, we have For the convergence of IIj, (j = 1,2,··· ,k), applying the same way as the convergence of I2in the proof Lemma 3.7 and using Hölder inequality, we only need to consider the convergence of and It easy to find that, for l =1,2,··· ,m, If l is odd, (3.9) is less than where in the last equality, we use similar arguments as in the proof of Lemma 3.1. If l is even, (3.9) is less than where we use Remark 1.2 in the first inequality and the proof of Lemma 3.2 in the second inequality. From (3.8), we can see (3.10) is less than a constant c. Then, For any γ >1, we define where Then,by(3.3)and Lemma 3.6,using similar arguments as the proof ofwe have Applying the same way as the convergence of IIj, (j =1,2,··· ,k),using Hölder inequality,we only need to consider the convergence of and We can see (3.14) is less than (3.10), which is less than a constant c. By some calculation, we can see (3.13) is less than Therefore, Making the change of variablesfor i=1,2,··· ,m (with the convention ym+1=0),we can rewrite For any ε ∈(0,1), we define where Let and where we use the same argument as in (3.3) in the second inequality, and use Lemmas 2.1 and 3.6 in the third inequality. This gives Making the change of variablesfor i=1,2,··· ,m again, we can rewrite where For any σi∈(i=1,2,··· ,k), define where Let Ωmbe the set of all (τ,σ1,σ2,··· ,σk−1) such that φτ,σ1,φτ,σ2,··· ,φτ,σk−1is bijective.Then, from Biane [3], the number of elements in Ωmis Define the set Thus,by Lemma 2.2,using the same argument as the proof Proposition 4.5 in[16],we have as ε →0 first, and then, γ →∞, where θ is (1 −2H)∧H if H ≤1/2 and 2 −2H otherwise. On the other hand, using the same way, we have Therefore, It is easy to find that where Γ(·) is a Gamma function, and by Lemma 3.1, we find that Define Combining (3.10), (3.15), (3.17) with(3.20), we have Proof of Theorem 1.1This follows from Lemmas 3.4–3.6 and Proposition 3.8.
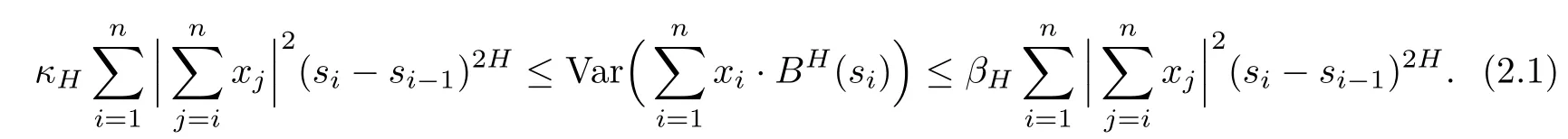
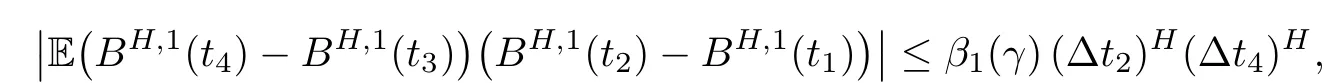
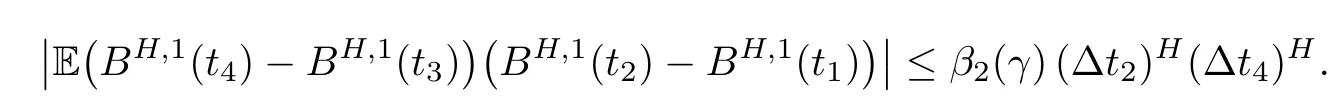
3 Proof of Theorem 1.1

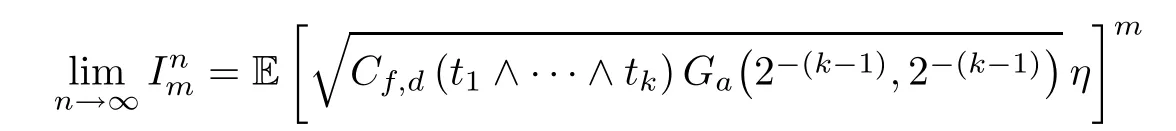

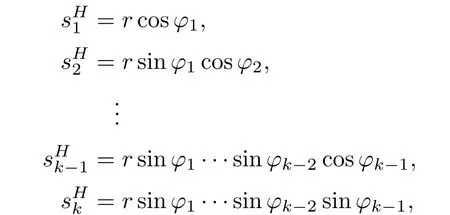

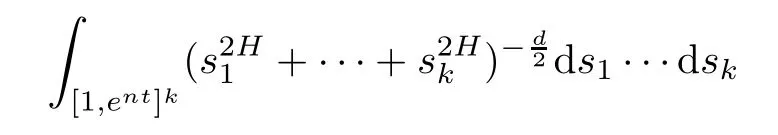
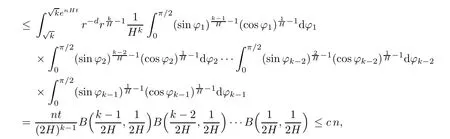



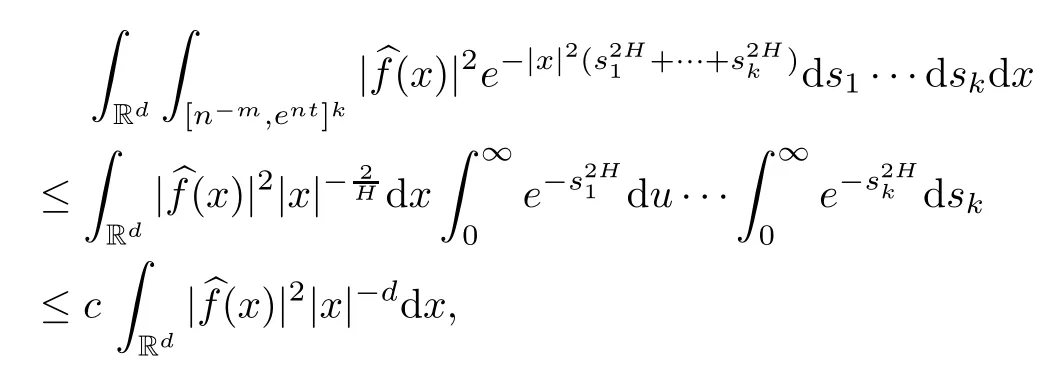
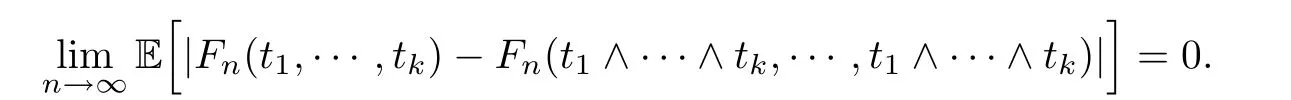

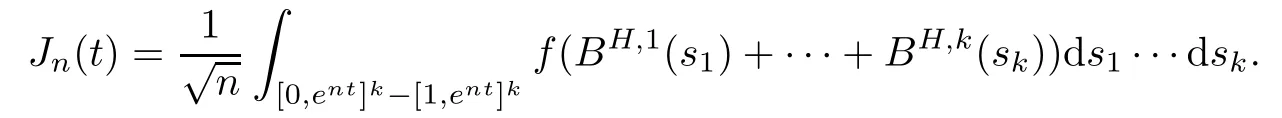
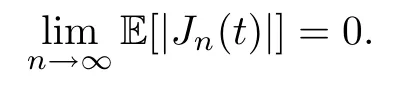
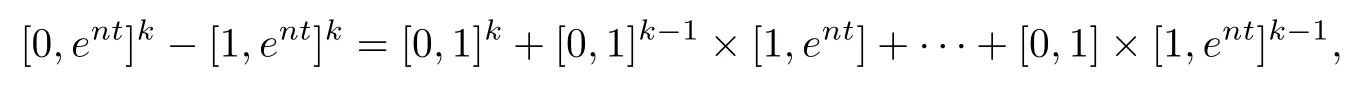
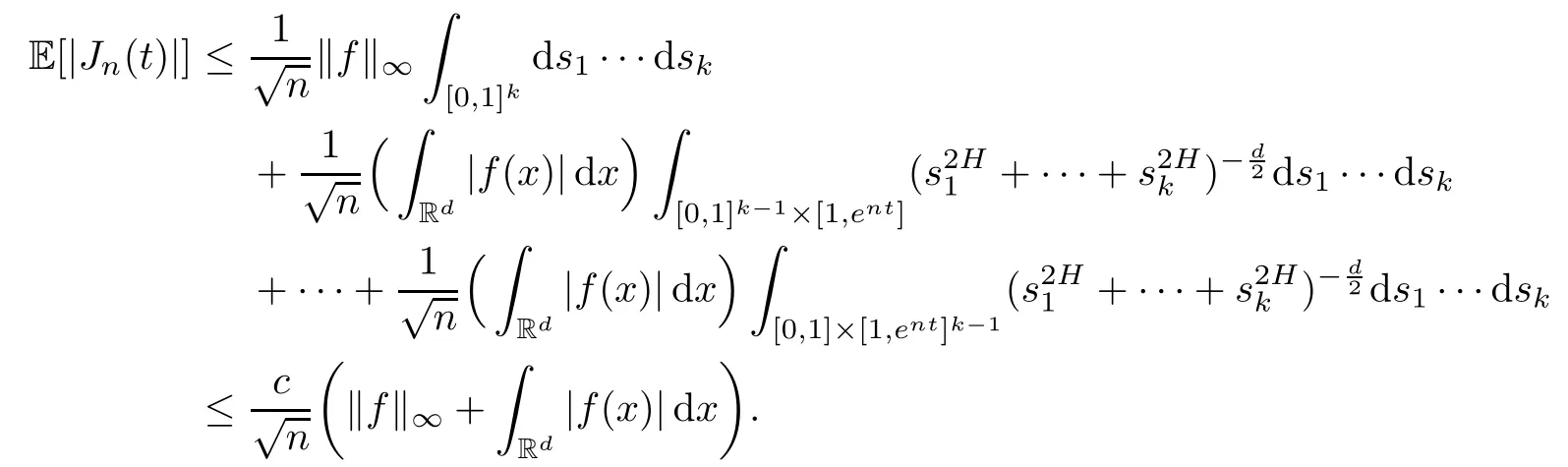
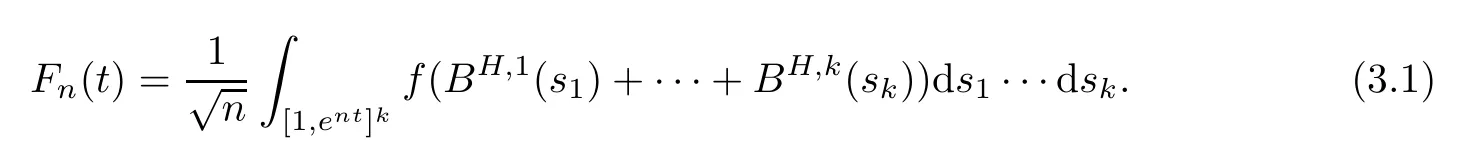
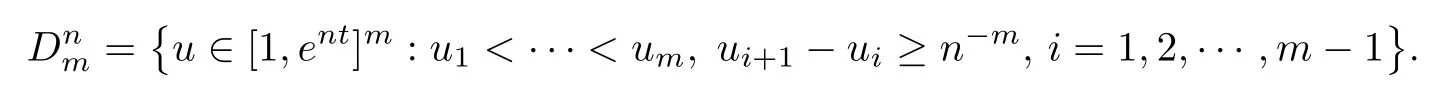

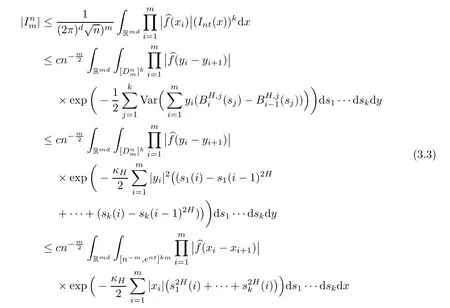
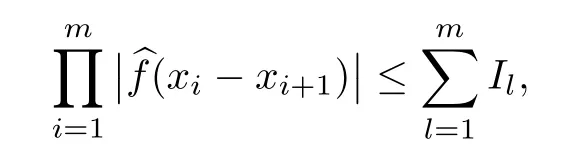
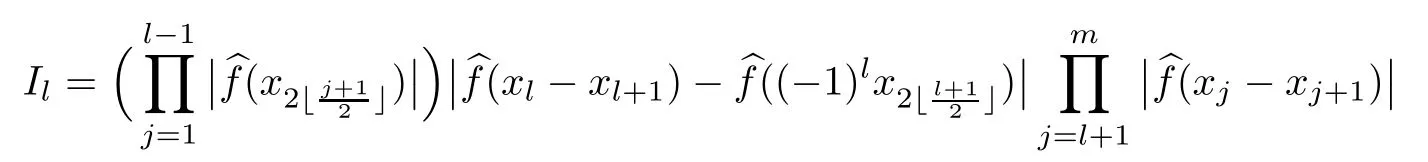
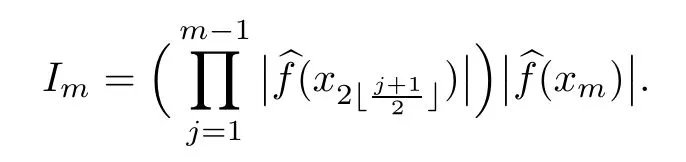

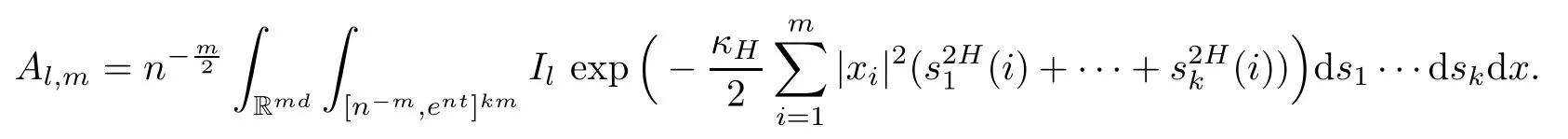

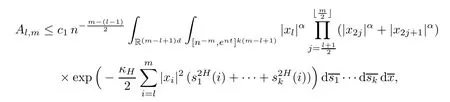

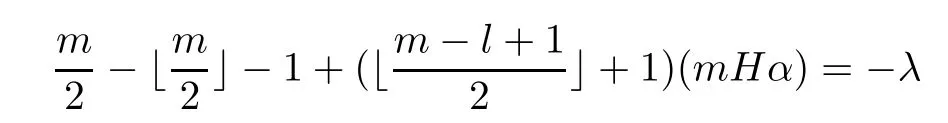

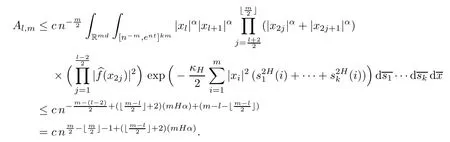


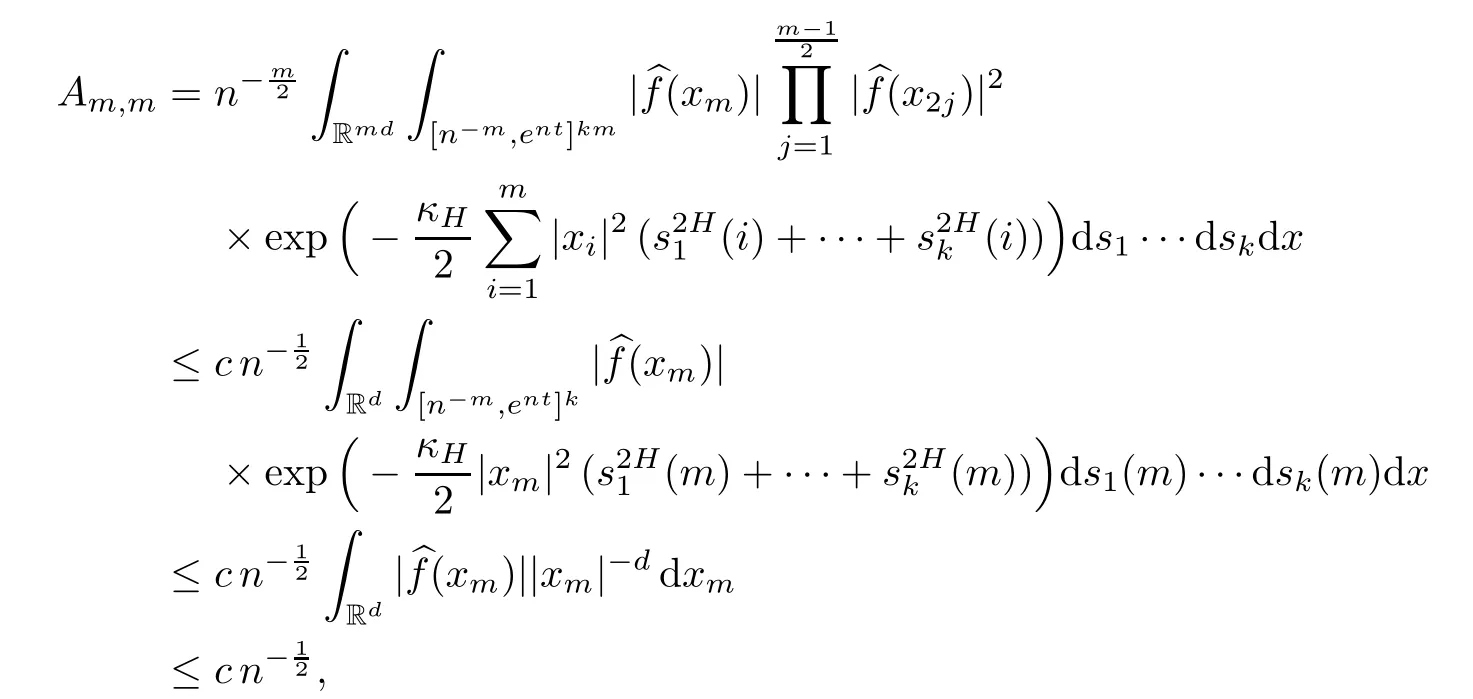


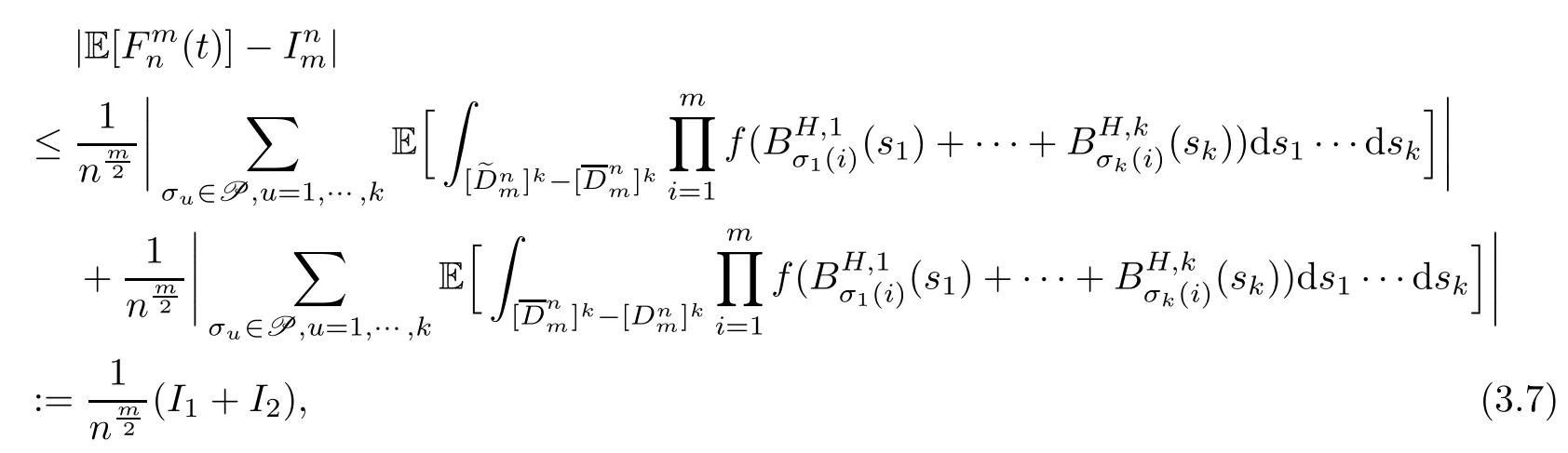



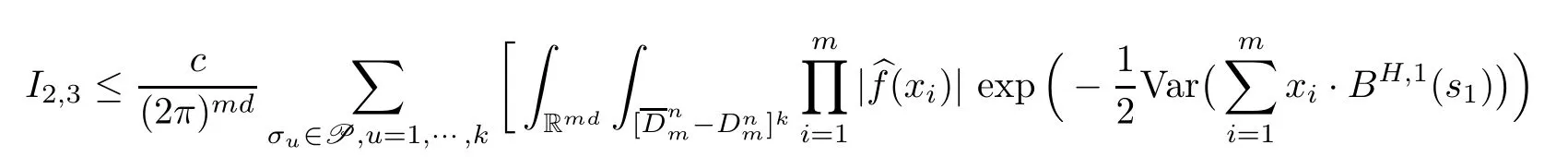
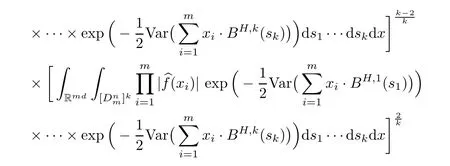
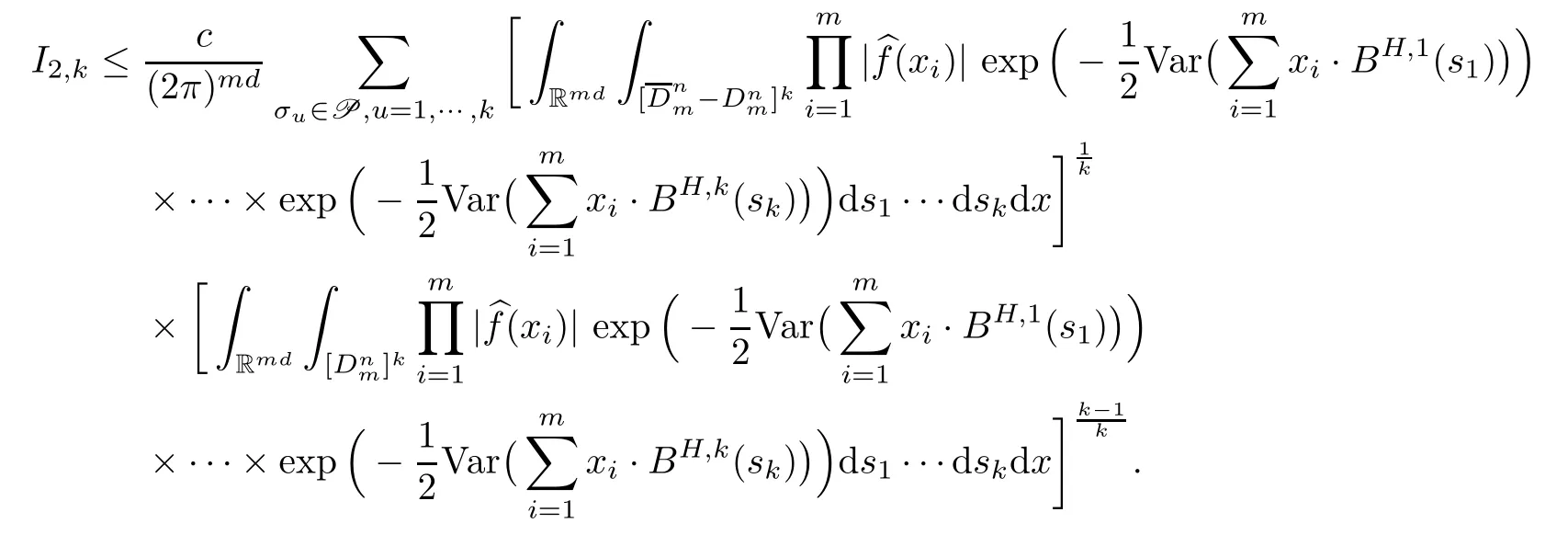
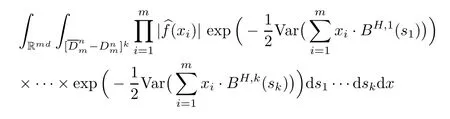
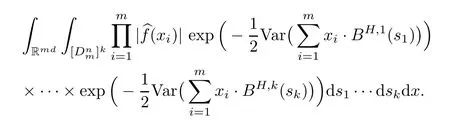
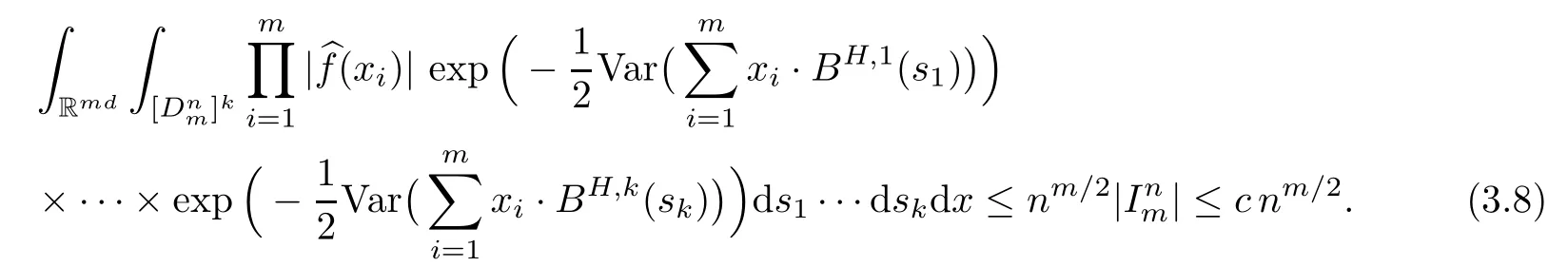
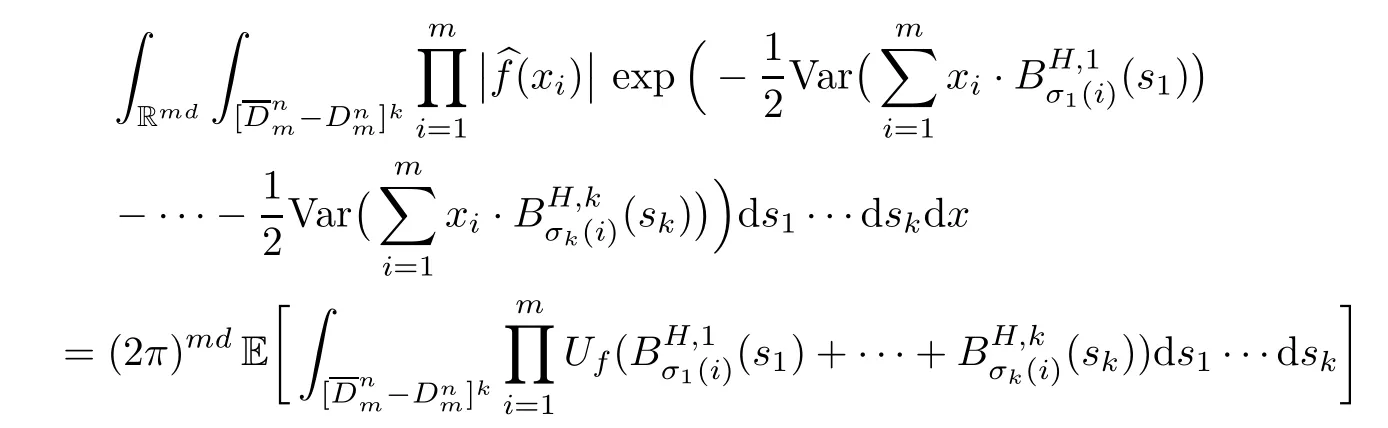
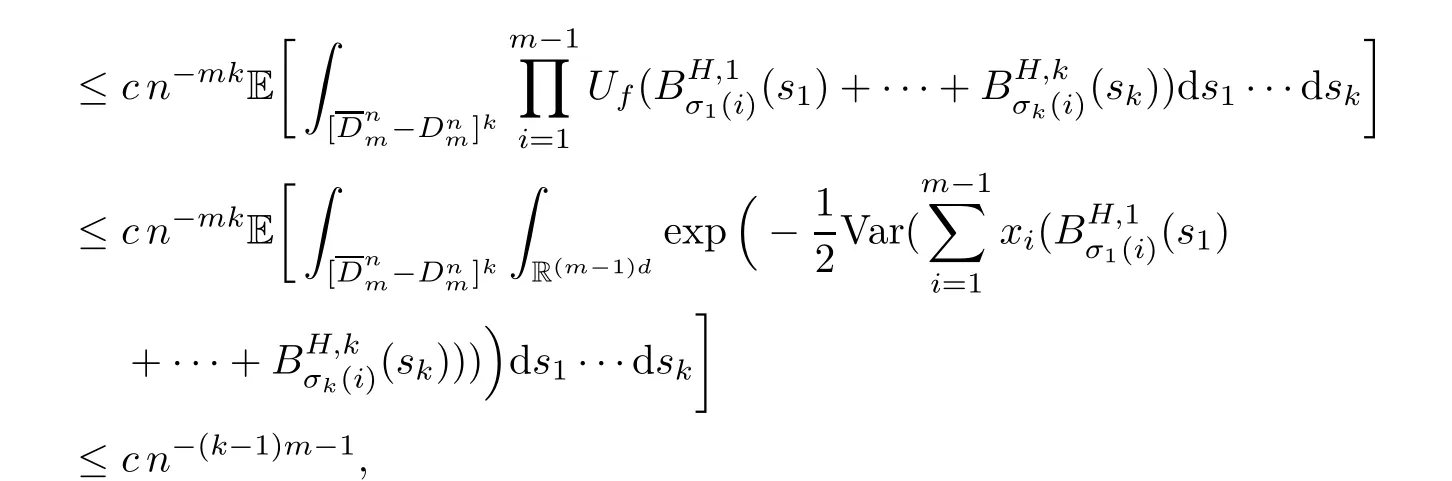




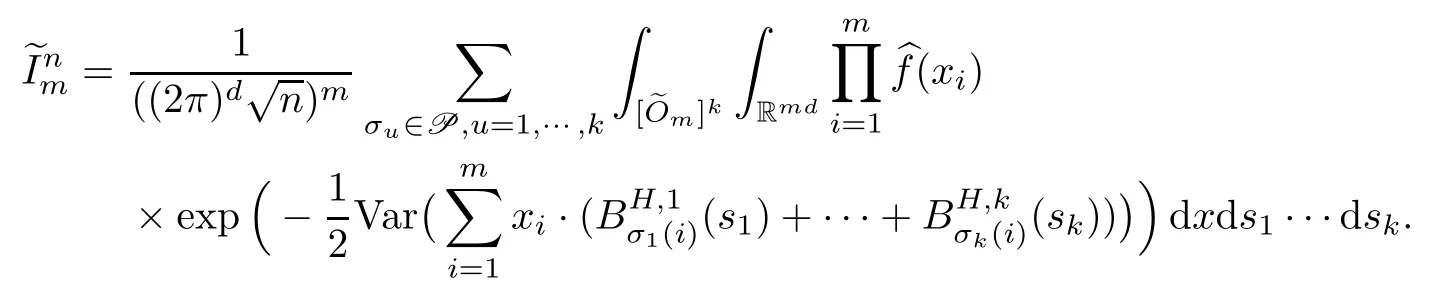
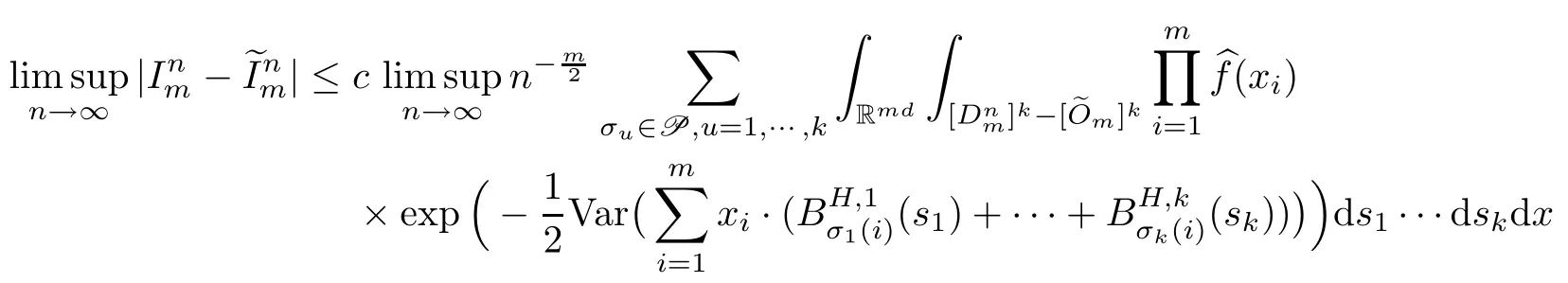

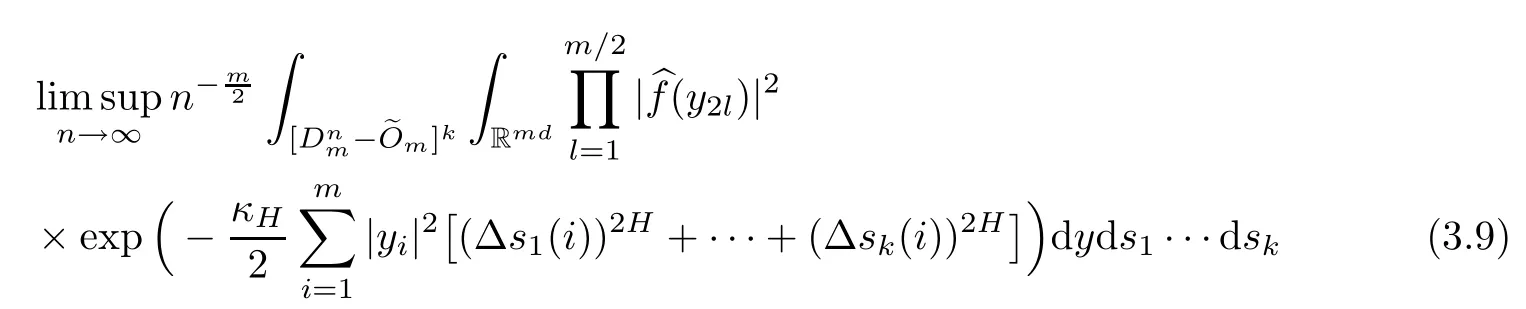
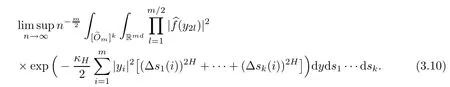
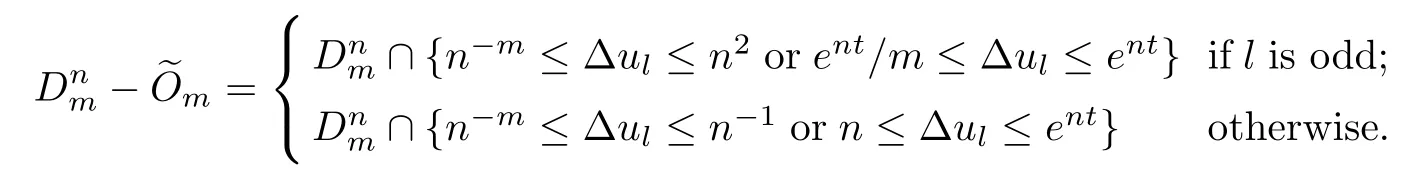

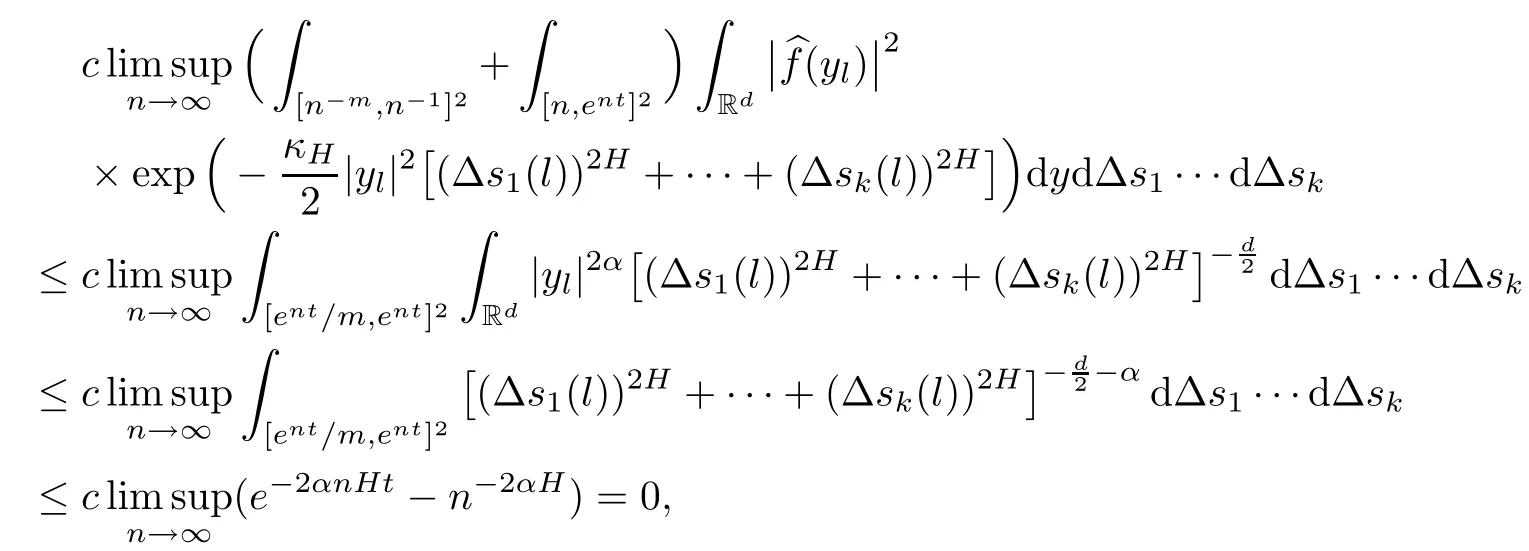

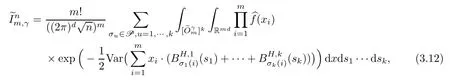
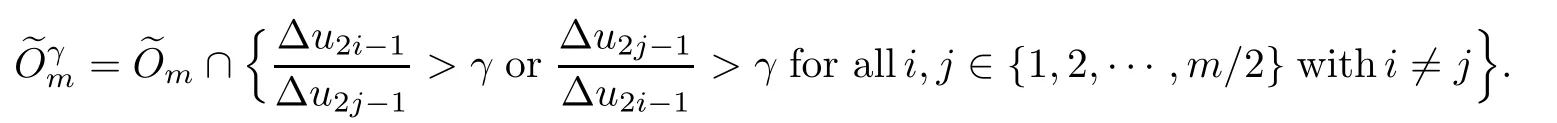
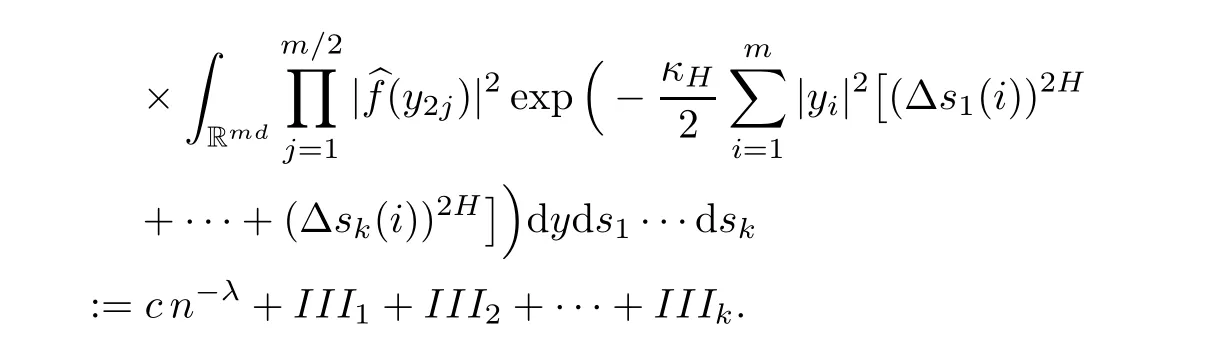
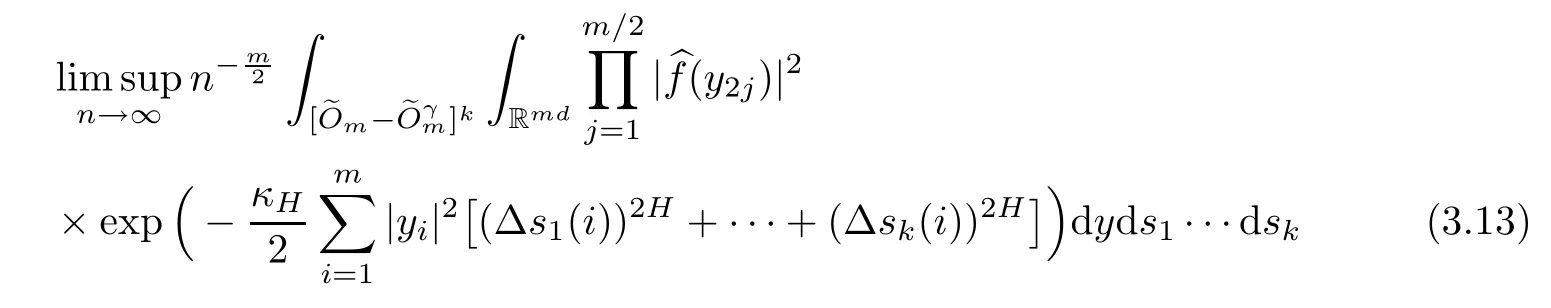
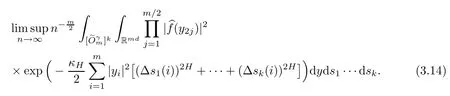
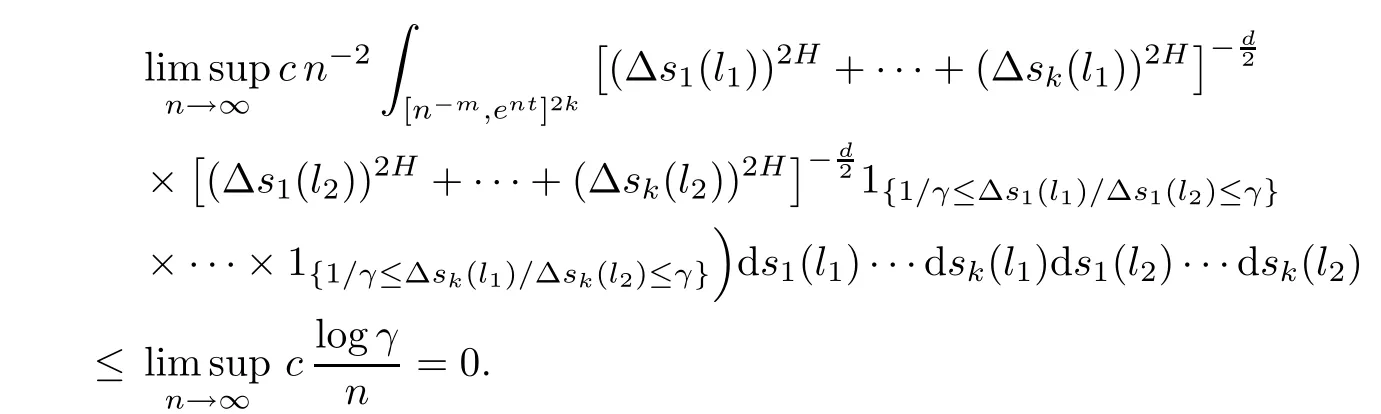

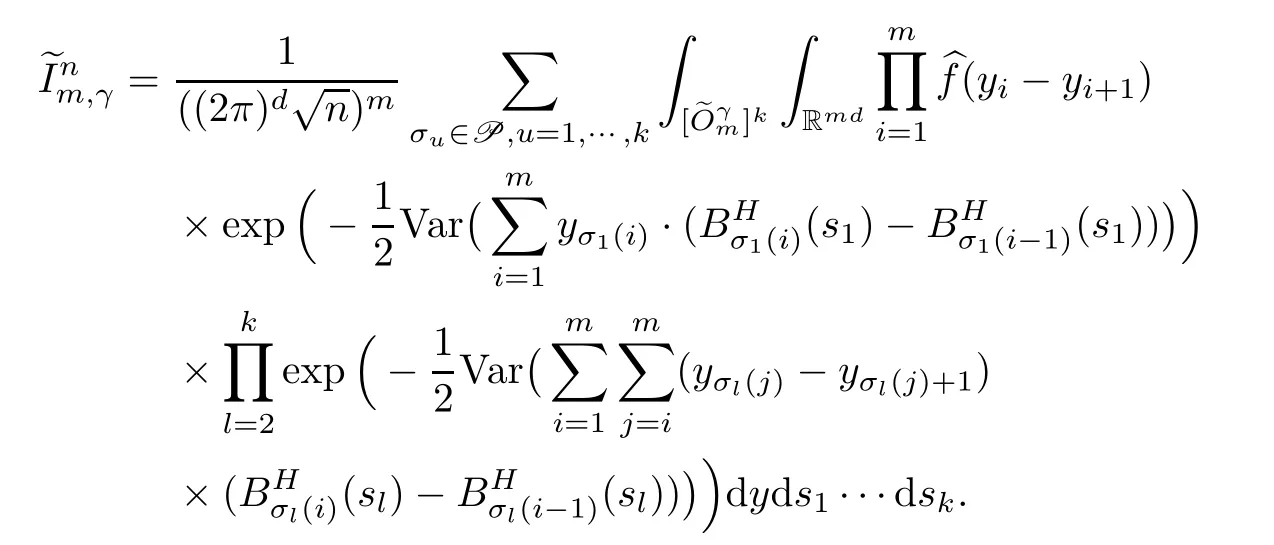
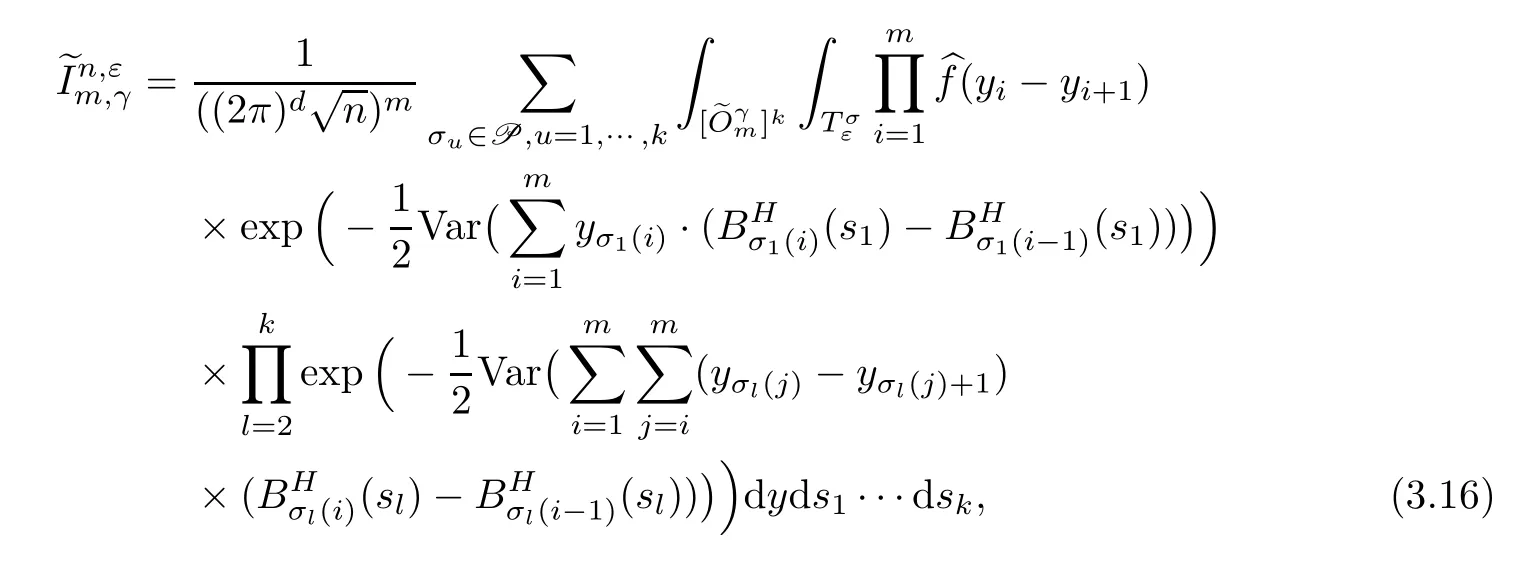
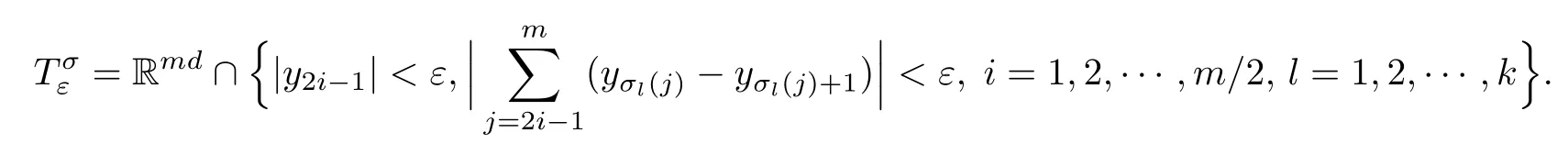

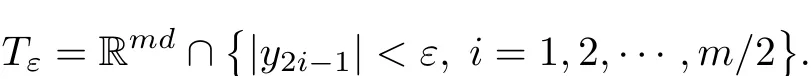


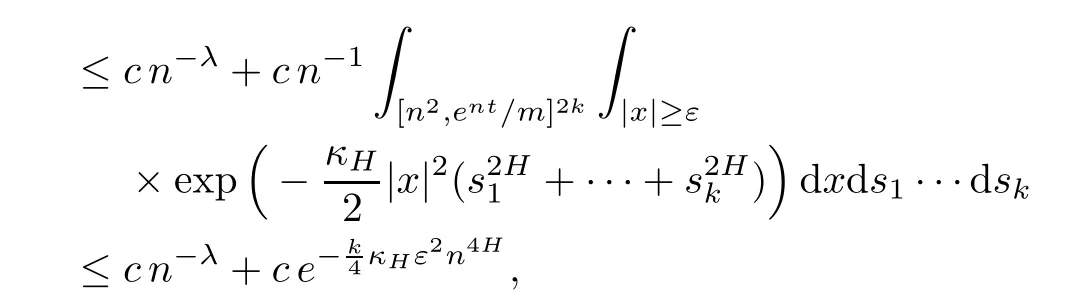





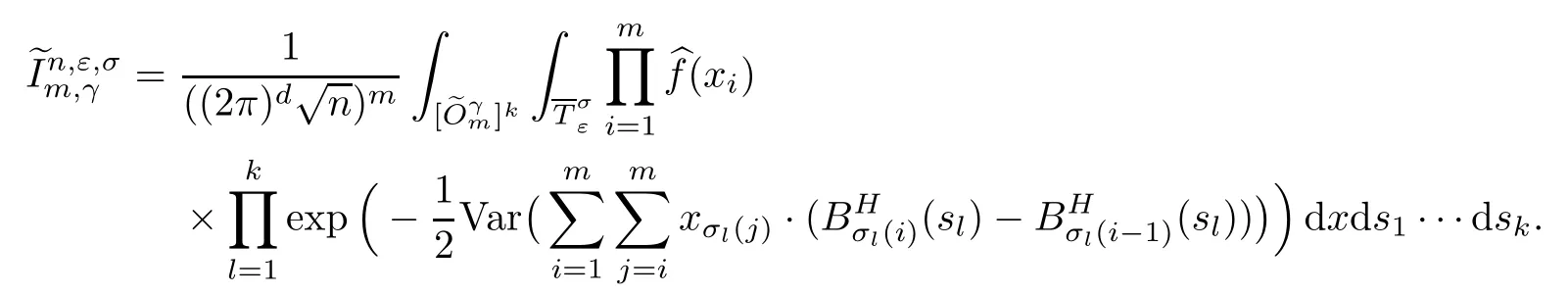
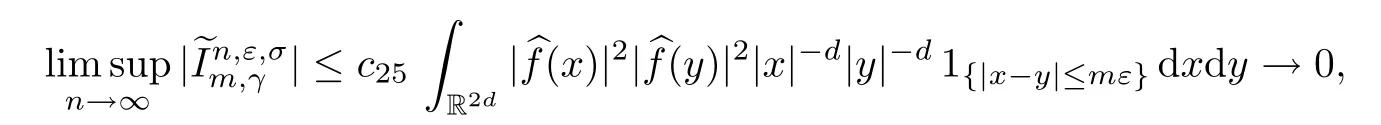
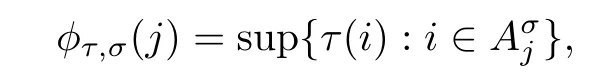
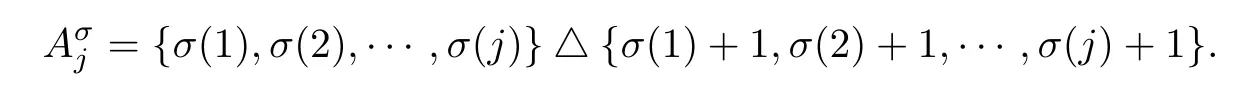
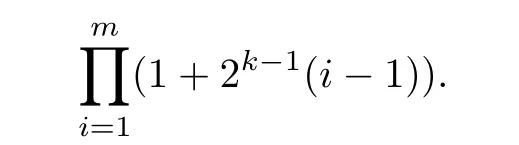
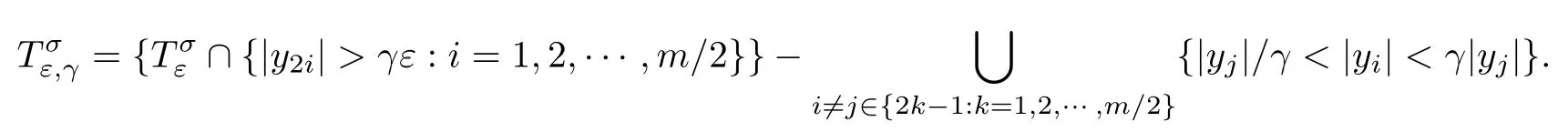
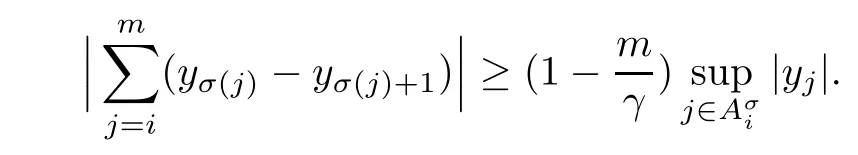

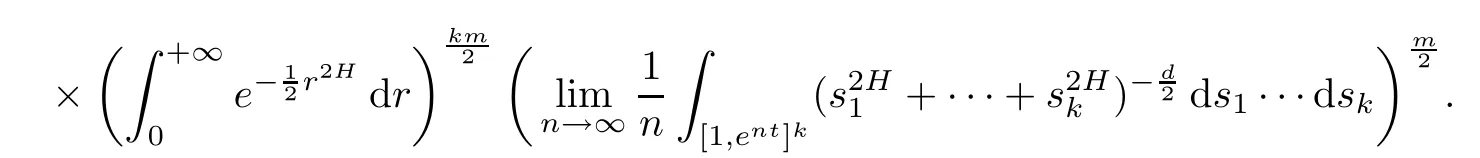

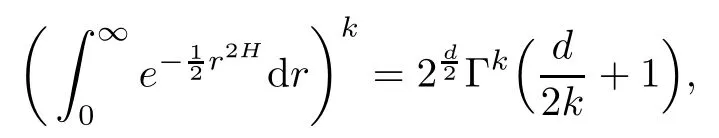
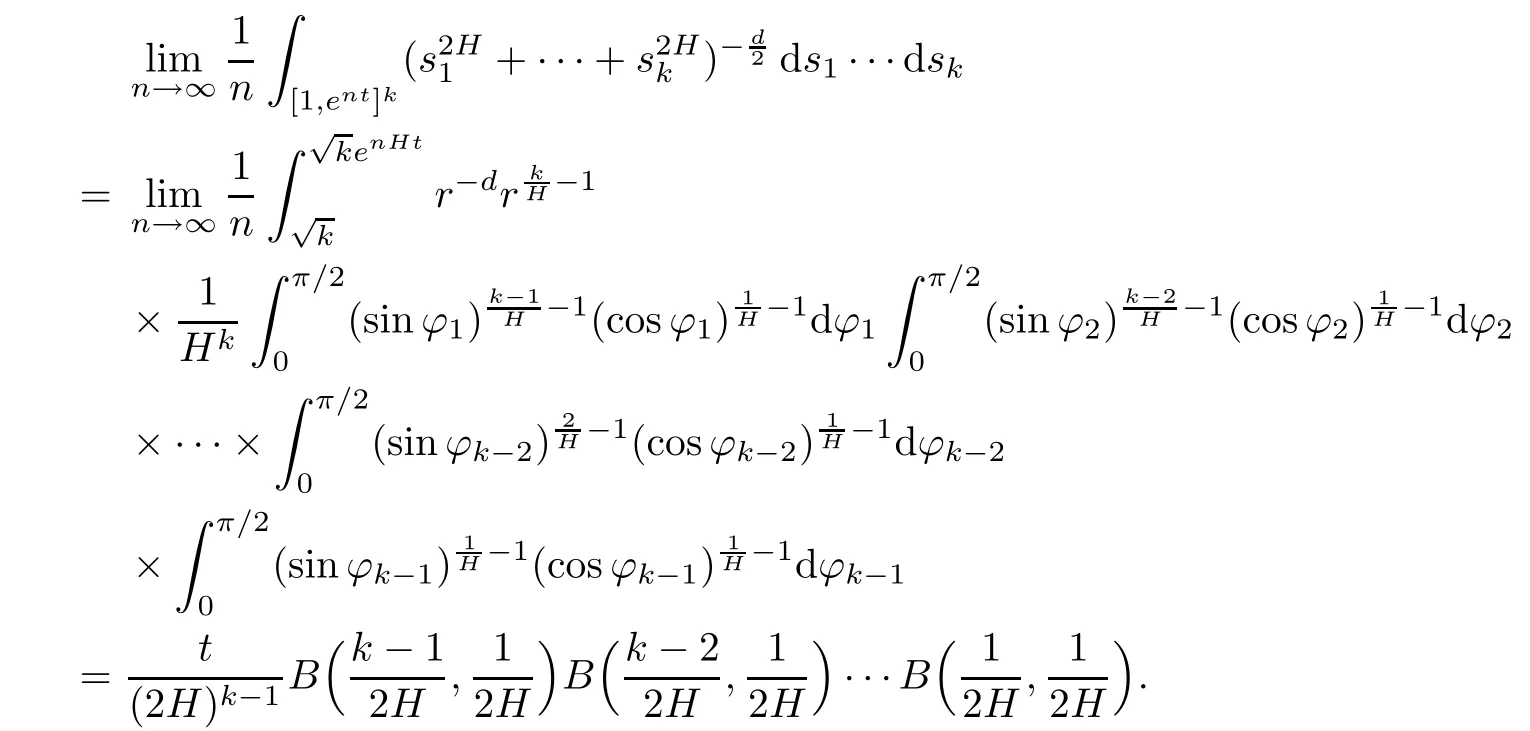
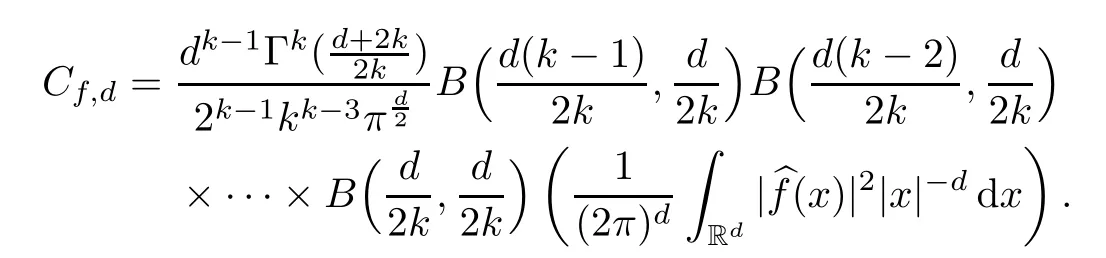
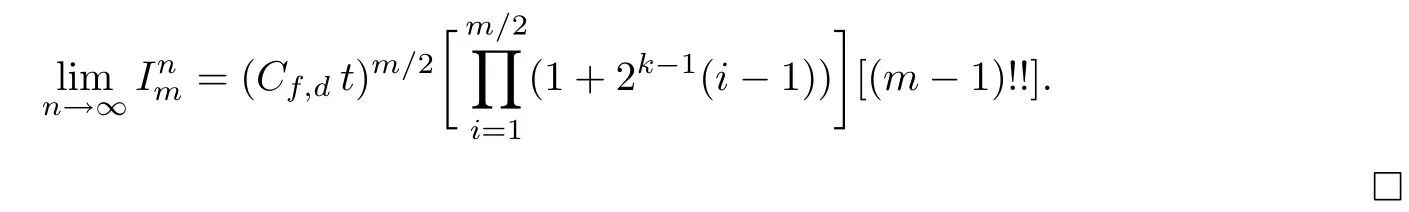
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- A VIEWPOINT TO MEASURE OF NON-COMPACTNESS OF OPERATORS IN BANACH SPACES ∗
- MINIMAL PERIOD SYMMETRIC SOLUTIONS FOR SOME HAMILTONIAN SYSTEMS VIA THE NEHARI MANIFOLD METHOD∗
- TOEPLITZ OPERATORS WITH POSITIVE OPERATOR-VALUED SYMBOLS ON VECTOR-VALUED GENERALIZED FOCK SPACES ∗
- LIE-TROTTER FORMULA FOR THE HADAMARD PRODUCT *
- AN ABLOWITZ-LADIK INTEGRABLE LATTICE HIERARCHY WITH MULTIPLE POTENTIALS *
- MULTIPLICITY OF POSITIVE SOLUTIONS FOR A NONLOCAL ELLIPTIC PROBLEM INVOLVING CRITICAL SOBOLEV-HARDY EXPONENTS AND CONCAVE-CONVEX NONLINEARITIES *
