MINIMAL PERIOD SYMMETRIC SOLUTIONS FOR SOME HAMILTONIAN SYSTEMS VIA THE NEHARI MANIFOLD METHOD∗
2020-08-02ChouhaSOUISSI
Chouhaïd SOUISSI
Department of Mathematics, Faculty of Sciences of Monastir, University of Monastir,5000 -Monastir, Tunisia E-mail: chsouissi@yahoo.fr
Abstract For a given T > 0, we prove, under the global ARS-condition and using the Nehari manifold method, the existence of a T-periodic solution having the W-symmetry introduced in [21], for the hamiltonian system Moreover, such a solution is shown to have T as a minimal period without relaying to any index theory. A multiplicity result is also proved under the same condition.
Key words Hamiltonian; variational; minimal period; Nehari Manifold
1 Introduction
We consider the following second order hamiltonian system

where z :R →RNis a vector function, N is a positive integer, and V′is the gradient vector of the potential function V with respect to z.
In [16], Rabinowitz proved the existence of non-constant periodic solutions with any prescribed period T >0, for system(1.1). He supposed that V is superquadratic at the origin and satisfies the well known Ambrosetti-Rabinowitz’s condition
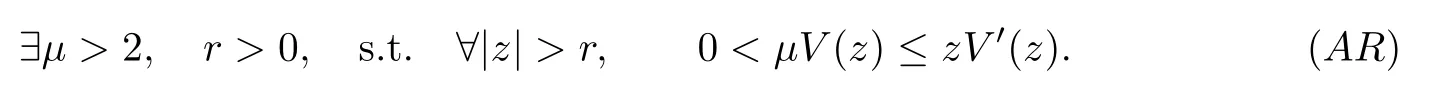
He also conjectured that (1.1) possesses a non-constant solution with any prescribed minimal period. Later(1985),Ekeland and Hoffer[8]made a significant progress by confirming this conjecture for strictly convex hamiltonian systems.
In the last years, many researchers has been based on (AR) in their proofs [1–6, 11, 13].Few of them did not use any convexity hypotheses in their works. One can refer to Girardi,Matzeu [9, 10], Long [12], and Souissi [20, 21].
In the last two references, the following new growth assumption was introduced,
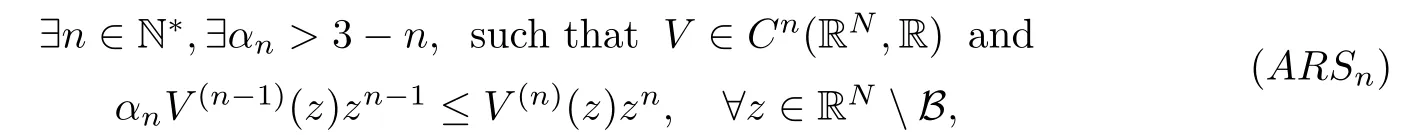
where V(n)is the nthderivative of V, for a given integer n ≥1. In [20], the author considered the global (ARSn)-condition(B = {0}). He proved, thanks to the saddle point theorem, the existence of at least one even periodic solution for problem(1.1). Then,in[21],he used the local condition(B =Br(0))and supposed the potential to be superquadratic at the origin. Using the Mountain-pass theorem, he proved the existence of at least one periodic solution of(1.1)which is not only even, but also satisfies the so called W-symmetry, introduced in that article and with which we will deal in the third section of this article. In both works,an iteration inequality on the symmetric Morse indices was used to study the minimal period of the solutions. This inequality is due to Long[12]. In [20], the solution has been shown to possess a minimal period T/k for some integer 1 ≤k ≤3. However, the W-symmetry introduced in [21] allowed to eliminate T/2 as a possible period for the solution of (1.1).
In this article, we use a technique different than that of [20, 21], consisting on the Nehari Manifold method combined with a variational approach. We prove, under the global (ARSn)-condition, the existence of periodic solutions of (1.1). Moreover, we improve the results given in the last two papers by showing that neither T/2 nor T/3 is a possible minimal period for the solutions of the the problem, without relaying to any index theory. We state our first main results as follows.
Theorem 1.1Assume that V satisfies the global (ARSn)-condition for some integer n ≥2. Suppose also that we have

Then, for every T >0, problem(1.1)has at least one periodic solution u with T as its minimal period. Moreover,u is even about 0 and T/2 and add about T/4 and 3T/4.
The second main result of our work will be related to the multiplicity of periodic solutions of (1.1).
Theorem 1.2Assume that (V1) and (V2) are satisfied and that the global (ARSn)-condition holds for some n ≥2. Then, for any T > 0, (1.1) possesses infinitely many pairs of T-periodic solutions, each of which is even about 0 and T/2 and add about T/4 and 3T/4.
2 Variational Formulation
Before starting our variational formulation,we state,as in[20],that we can replace,without loss of generality, in Theorem 1.1, the condition (V1) by

To look for solutions of (1.1), we denote

and consider the Sobolev space

equipped with its usual norm
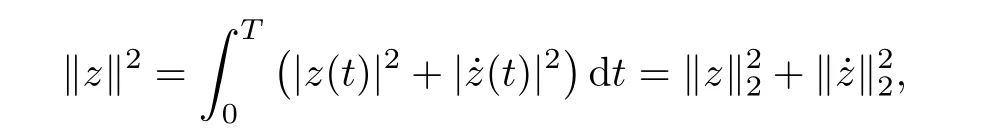
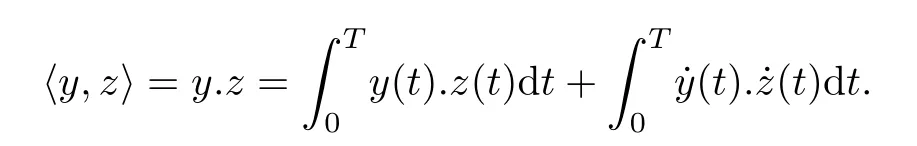
Moreover,the functional Φ, defined on ETby
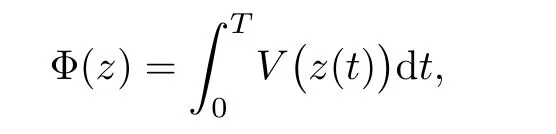
is weakly continuous and Φ′:ET→is compact.
We define on ETthe functional

It is easy to prove that f ∈Cn(ET,R)and to see that the solutions of(1.1)are the critical points of f.
3 Some Symmetry Properties of f and Related Consequences
In this section, we are interested in non-trivial critical points of f. For this, we define the W-action for any T-periodic function z :ST→RN, where

with

We recall some useful definitions, previously introduced in [21].
Definition 3.1A T-periodic vector function z :ST→RNis said to have
(1) the W-symmetry if δz =z, for ∀δ ∈W.
(2) the W-anti-symmetry if δz =−z, for ∀δ ∈W.
Definition 3.2A functional f, defined on ET, is said to be W-invariant if
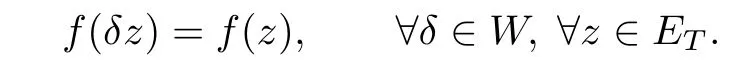
We consider the following subspace of ET

SETis a closed subspace of ETand as an immediate consequence of Lemmas 3.2 and 3.6 in [21], we have
Lemma 3.3If z ∈SET, then z is even about 0 and T/2 and odd about T/4 and 3T/4.Moreover,we recall the following results.
Lemma 3.4([21]) If V satisfies (ARS2), then the following assertions are equivalent:
(1) z is a critical point of f on SET;
(2) z is a C2(ST,RN)-solution of (1.1), and it has the W-symmetry.
Lemma 3.5([21]) Suppose that(ARSn)is satisfied,then(ARSk)is also satisfied for any integer k such that 1 ≤k ≤n −1.
Because of these lemmas, we will look, in the next, for non trivial critical points of f on SET. To do this, we define the constants M and m as follows:
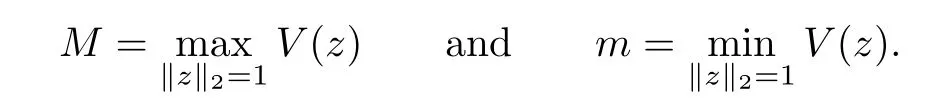
Then, we can state
Lemma 3.6We have
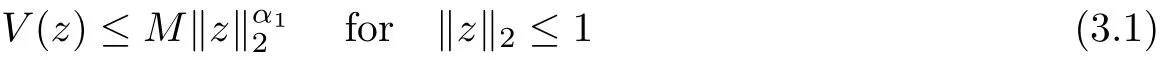
and
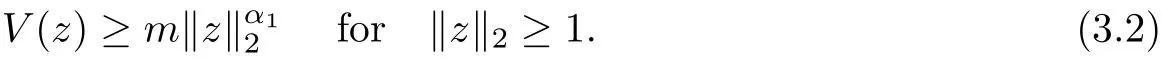
ProofBy Lemma 3.5, V satisfies (ARS1). Then, the result follows immediately because of Mawhin and Willem [14].
This allows us to recall the next compactness result.
Lemma 3.7([21]) If () and (ARS1) hold, then f satisfies the Palais-Smale condition(PS) on ETand SET.
4 The Nehari Manifold
We use a different approach than those of [20] and [21]. We are interested in the Nehari manifold method to prove the existence of critical points of f. For this, we consider the functional h defined on SETby
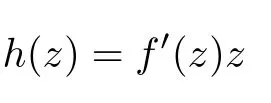
and define the Nehari Manifold
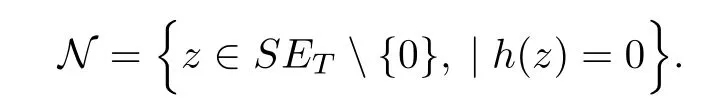
For z ∈SET{0}, we consider the function
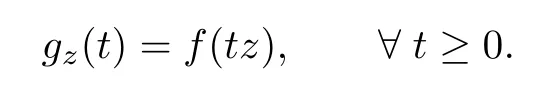
Then, we have the following proposition.
Proposition 4.1(1) For t>0,(t)=0 if and only if (tz)∈N.
Proof(1) Take t>0. It is sufficient to see that

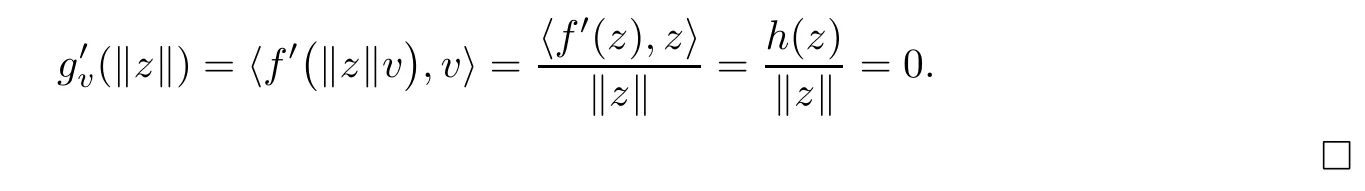
It is obvious that if z ∈SET{0} is a critical point of f, then z ∈N and f′(z)=0. The converse is given by the following lemma.
Lemma 4.2Suppose that V satisfies (ARS2), then every critical point of f on N is also a non trivial critical point of f/Non SET.
ProofBecause of (ARS2), we have
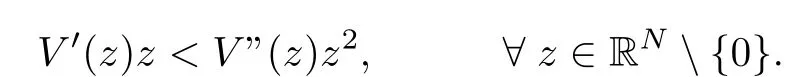
Then, for all z ∈N,
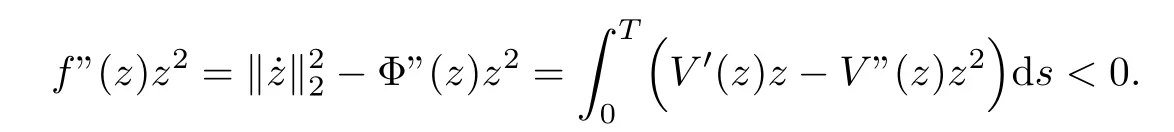
By the implicit functions theorem, N is a C1-manifold of codimension 1 in SET. Then,taking z ∈N such that f′(z)=0, and by the Lagrangian Multipliers method, we deduce that

which implies that

It follows that λ=0, and so f′(z)=0.
Lemma 4.3For any z ∈SET, we have

ProofTake z ∈SET. We have

which means that
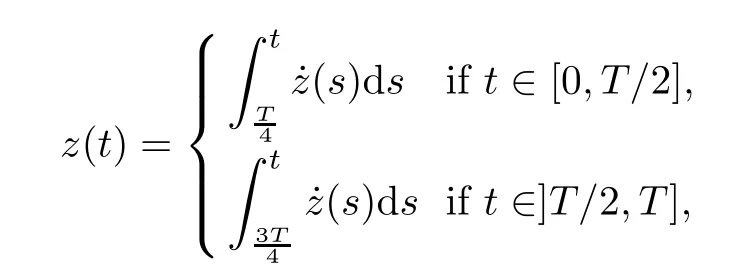
and the result follows.
Lemma 4.4For z ∈SET{0}, gzhas at least one critical point tz>0.
ProofTake z ∈SET{0}. On the one hand, we have, by 3.1 and 4.1,
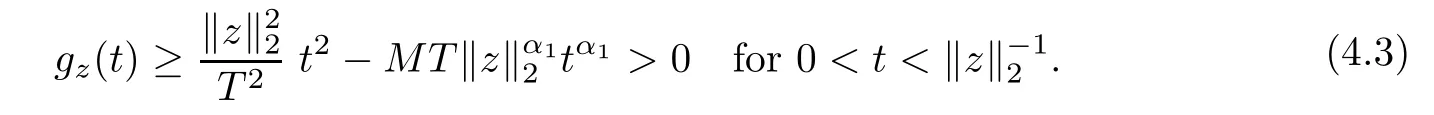
On the other hand, by 3.2 and 4.1,
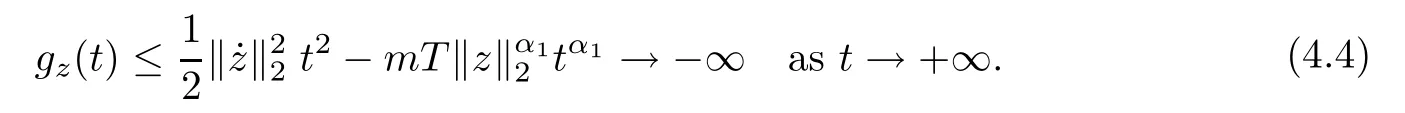
As gz(0)=0 and gzis of class C1, using (4.3) and (4.4), we obtain the result.
Lemma 4.5Let z ∈SET{0} and consider 0 Then, there exists t3∈(t1,t2), such that ProofLet 0 < t1< t2be such thatThen, there exists t3∈(t1,t2),such that As then we have Using (ARS2), we obtain Finally, by (ARS1), we have Lemma 4.5 implies,in particular,that the function gzcan not be constant over any interval of R+. In other words, the critical points of gzare isolated. As a consequence, we can prove the following uniqueness result. Lemma 4.6For z ∈SET{0}, the critical point tzof gzis unique. ProofAs gz(0)=0, we deduce by (4.3)that gzis strictly increasing near zero. Let tzbe the first maximum of gz. Then, Define szas follows: As tzis a maximum of gz, then we have obviously On the other hand, by Lemma 4.5, there exists uz∈(tz,sz), such that This contradicts (4.5) and the result follows. The last Lemma allows to give a new definition of N, that is, where tzis defined in Lemma 4.6. Lemma 4.7 ProofFor z ∈S and 0 Then, fixing ε>0, there exists tε>0, independent of z, such that This means that And so, Next, we denote by S the unit sphere of SET, that is, Lemma 4.8There exists δ >0 such that tz>δ for all z ∈S. ProofIt is an immediate consequence of the proof of Lemma 4.7. In fact, any δ ∈(0,tε)gives the result. Lemma 4.9f satisfies the PS-condition on N. ProofAssume that (zn)n≥0⊂N is a PS-sequence for f. Then, there exists C >0 such that and As zn∈N, then f′(zn).zn=0 and so by (ARS1), Combining the last inequality with (4.6), we obtain On the other hand, as Φ′is compact, passing to a subsequence,converges strongly. Then, writing we deduce that (zn)n≥0contains a convergent subsequence to a point z ∈N. Next, we define the following maps Lemma 4.10For each compact subset W of S, there exists a constant CW> 0, such that ProofWe argue by contradiction and suppose that there exists a compact subset W of S and a sequence (tn,zn)n≥0of (0,+∞)×W, such that As W is compact, passing to a subsequence, zn→z ∈W. Denote and Denoting by λ the Lebesgue measure on R, it becomes obvious that λ(Z)>0. On the other hand, the embedding of ETinto C(ST,RN) is compact, which means that It follows that there exists n0∈N, such that Then, by (3.2), we have Finally, we have This contradicts Lemma 4.7 and the result follows. Lemma 4.11m is an homeomorphism from S to N. ProofBy Lemma 4.4, then m is bijective. We just need to show that m is continuous.Let (zn)n≥0⊂S be a convergent sequence to z ∈S and write Consider the set W is a compact subset of S and by Lemmas 4.8 and 4.10, Then, as n →+∞, we have -up to a subsequence- thatand so, As N is closed in SET, then ()∈N and so=m(z). Next, we denote by Tz(S) the tangent space of S at z, that is, We recall the following result. Lemma 4.12([19], Corollary 1.3) We have the followings: (1) Ψ ∈C1(S,R) and (2) If (zn)n≥0is a PS-sequence of Ψ, then(m(zn))n≥0is a PS-sequence of f; (3) If (zn)n≥0⊂N is a bounded PS-sequence of f, then(m−1(zn))n≥0is a PS-sequence of Ψ; (4) z is a critical point of Ψ if and only if m(z)is a non-trivial critical point of f. Moreover,the corresponding values of Ψ and f coincide and (5) If f satisfies the PS-condition, then it is the same for Ψ; (6) If f is even, then so is Ψ. According to Lemmas 4.7 and 4.12, By Ekeland’s variational principle [7], there exists a minimizing sequence (yn)n≥0for Ψ such that Up to a subsequence, the PS-condition implies that there exists y ∈SET, with Thus, y is a critical point of Ψ. Again, because of Lemma 4.12, m(y) is a critical point of f, which is also a non-constant T-periodic solution of (1.1). In the next, for every non-constant T-periodic solution z of (1.1), define Suppose that O(z)=k ≥2 and define the function Then, y ∈SETand by Lemma 4.4, there exists>0, such that (y)∈N. It follows that As z is (T/k)-periodic, we deduce that Now, the unique critical point of gz, given by Lemma 4.6, is showed to be a maximum (in the proof of Lemma 4.4). As z ∈N, then by Proposition 4.1, we deduce that tz=1, so This means that This is absurd and then O(z)=1. We need the following theorem, which proof can be found in [15]. Theorem 6.1Let H be a Hilbert space such that the unit sphere S in H is a submanifold of class C1and let Φ ∈C1(S,R). If Φ is bounded from below and satisfies the PS-condition,then c=is attained and is a critical values for Φ. If, in addition, Φ is even, then Φ has infinitely many pairs of critical points. In Theorem 6.1, we consider the space By (V2) and Lemma 4.12 (5), we deduce that Ψ is even. By Lemma 4.7, we have As Ψ satisfies the PS-condition, then Theorem 6.1 yields that Ψ has infinitely many pairs of critical points on S. Again by Lemma 4.12, f has infinitely many pairs of critical points. Thus, (1.1) has infinitely many pairs of periodic solutions on SET.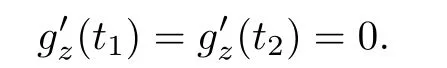

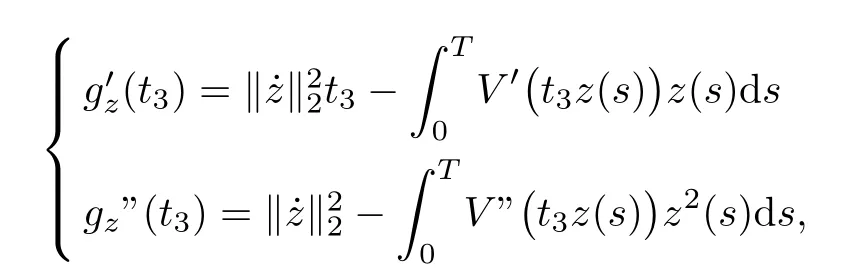
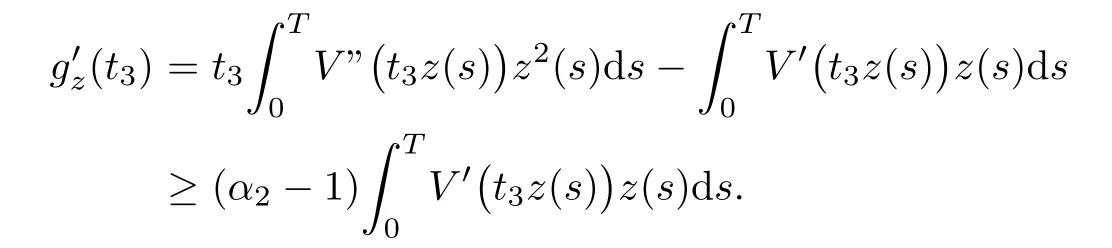
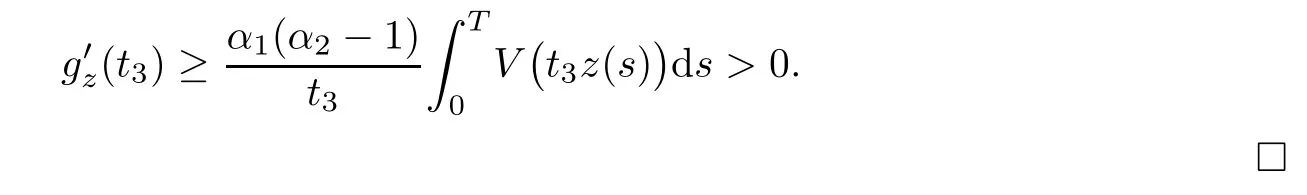
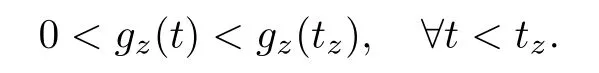
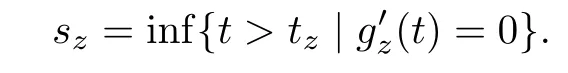

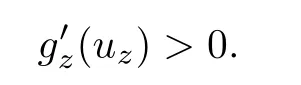
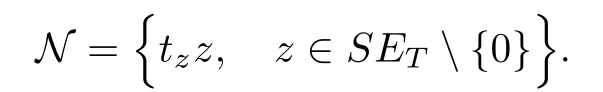
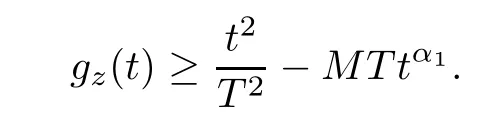



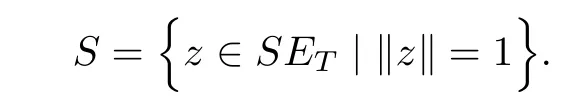
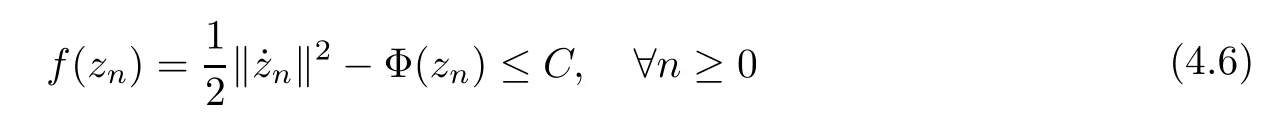


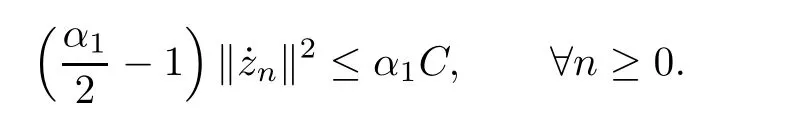



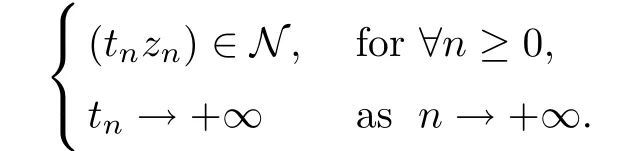
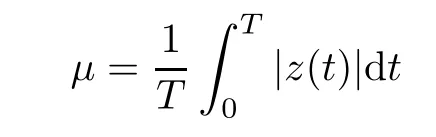
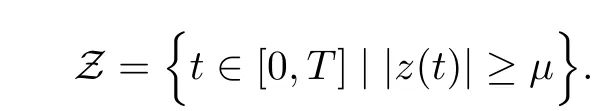
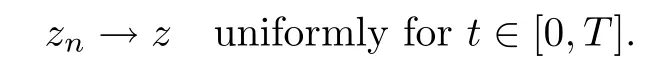

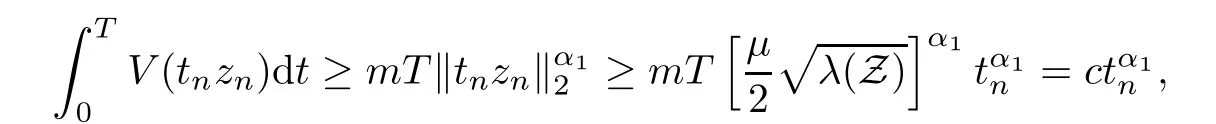
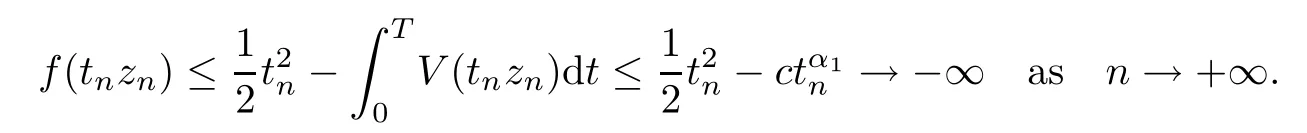
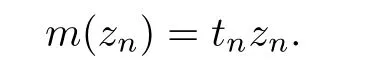
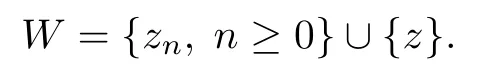
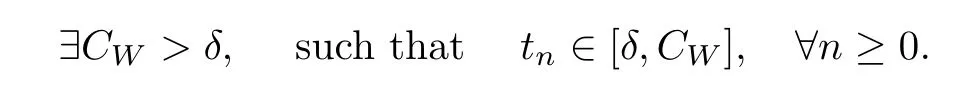


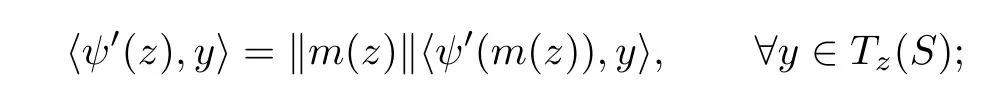
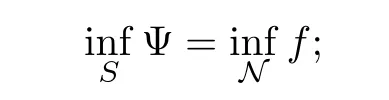
5 Proof of Theorem 1.1
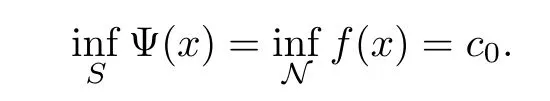
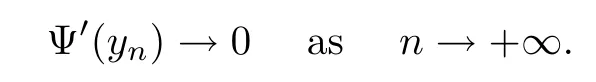
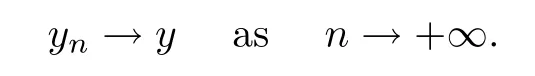
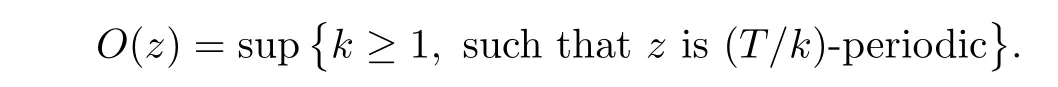
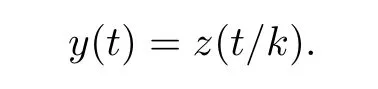
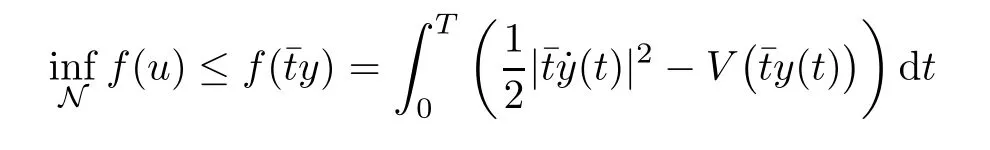
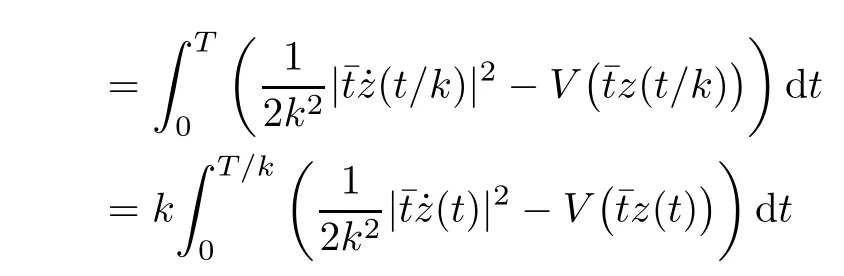
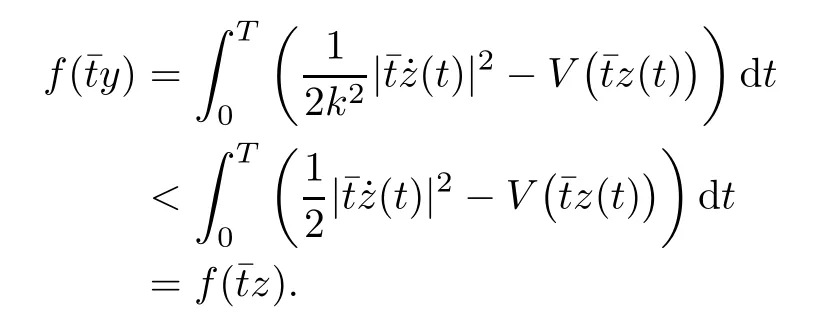
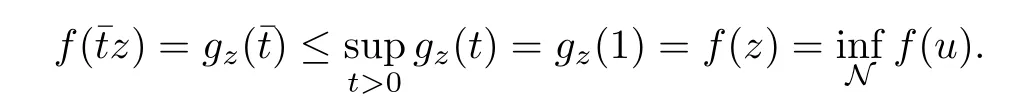

6 Proof of Theorem 1.2

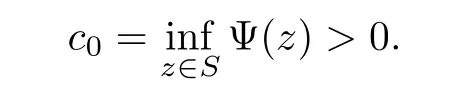
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- A VIEWPOINT TO MEASURE OF NON-COMPACTNESS OF OPERATORS IN BANACH SPACES ∗
- TOEPLITZ OPERATORS WITH POSITIVE OPERATOR-VALUED SYMBOLS ON VECTOR-VALUED GENERALIZED FOCK SPACES ∗
- LIE-TROTTER FORMULA FOR THE HADAMARD PRODUCT *
- AN ABLOWITZ-LADIK INTEGRABLE LATTICE HIERARCHY WITH MULTIPLE POTENTIALS *
- MULTIPLICITY OF POSITIVE SOLUTIONS FOR A NONLOCAL ELLIPTIC PROBLEM INVOLVING CRITICAL SOBOLEV-HARDY EXPONENTS AND CONCAVE-CONVEX NONLINEARITIES *
- ASYMPTOTIC CONVERGENCE OF A GENERALIZED NON-NEWTONIAN FLUID WITH TRESCA BOUNDARY CONDITIONS∗
