基于实测数据的土石坝风险分析研究
2020-08-01杨泽煌
杨泽煌
(德安县水务局,江西 德安 330400)
1 概 述
风险评价作为大坝安全评价的新内容,涉及大坝风险标准、管理决策等领域。随着水库风险理念的深入与应用,风险分析逐渐成为水利界的研究热点,并成为风险管理的决策工具。过去,大坝风险的研究形式多种多样,从不同的角度出发,风险评价结论形式有所不同,其应用实践也有所不同[1]。以概率统计为方法、风险率为度量指标是风险评价的重要形式,将传统的定性结论向定量过渡,对于开展风险管理有着非常积极的意义。但是,该方法基于对不确定性数据采取合理的定量分析,数学模型的逻辑要严密。在复杂的大坝安全评价中,常常因为缺失数据而进行简化假设,以致影响风险分析方法的推广运用。风险分析方法在水利工程中已积累了一些经验及方法[2],本文以大坝渗流与滑坡稳定为对象,以概率的视角,探讨大坝风险分析方法,为了解大坝安全程度、开展风险评价提供参考依据。
2 风险分析实用模型
2.1 大坝风险模型
传统安全评价根据规范的定性或定量要求,采取合适的现场检查与理论评价进行判断。现场检查内容主要根据现象有无异常,结合现场检查进行理论反演计算。如结合监测数据,分析渗透坡降是否大于允许坡降;结合边坡及土质,分析坝坡稳定系数是否大于1等等,这种传统的评价方法基于确定性的数量采取定性判断。风险分析主要指由定性判断向定量转换,并以概率大小表示,这种表示方式也成为普遍发展趋势。但由于两种方法的评价体系、评价方法不一致,很难直接将定性判断直接向风险概率转换,需要大量的经验及统计,目前,已有不少经验统计将定性描述转化成概率大小,但这种转换过于粗略,约束条件较多,难以在实际应用进行推广。
大坝风险属系统风险,风险要素涉及广泛,但综合分析风险分析往往采用基于独立的前提下开展的。即大坝风险Ri由n个相互独立的风险要素组成的抗力R、m个相互独立的风险要素组成的广义荷载S,荷载S与抗力R的联合密度函数为fRS(r,s),则大坝安全风险率Ri为[3]:
(1)
式中:Ri为安全风险率;R为单因素抗力;S为单个荷载的作用;Pf为广义抗力R小于广义荷载S的概率;fRS(r,s)为联合密度函数。
由于大坝系统复杂,风险要素关联性难以统一表示,建立fRS(r,s)是比较困难的。因此,将各风险要素作为独立或少数几个联合变量进行考虑。在安全评价过程中,主要影响因素包括防洪、变形、渗流和应力应变等,采取有效方法将这些因素的量值控制在允许的范围内,是保证大坝安全运行的关键。因此,可将大坝风险因素分为防洪、结构、渗流等指标作为风险评价指标,进行单独分析。
2.2 滑坡失稳风险分析
根据可靠度原理,在设计洪水位条件下,滑坡失稳事件概率Pf1可定义为:
Pf1=Pf1(S≥R)=1-Ф(β)
(2)
根据文献可知[4],安全系数K0与可靠指标β1存在某种关系,Pf1可表示发生的边坡失稳风险率:
(3)
其中:
(4)
(5)
式中:K0可按坝坡稳定计算求得;δR为抗力变异系数;δR=σR/μR;δS为荷载变异系数;δS=σS/μS;K0=μR/μS为中心安全系数,μR与μS分别为抗力及荷载的均值,根据导则给出安全系数的等级划分,见表1。
将K0代入式(3)-式(5)中,并取δR=δS=0.1[4],求得相应的β1和洪水位下的失稳风险率Pf,其关系见图1。
由图1可知,在设计洪水位时,随着安全系数的增大,发生边坡失稳的概率逐渐减小。根据《导则》给出的安全系数,当安全系数相差在0.2~0.3,风险率相差却非常大,最大风险率Pf为5.3%,而最小风险率Pf仅为0.04%,风险相差100倍左右,这与坝坡越平缓、滑坡的可能性越小的实际情况相符合。

图1 不同大坝安全级别的边坡失稳风险率分区图
2.3 渗流稳定风险分析
土石坝渗流稳定涉及要素复杂,包括外界荷载上下游水位、坝体坝基的土质特性及防渗体系是否完善等,除外界水位外,其它参数的不确定性较明显,进行定量分析时难以控制,在构建密度函数为fRS(r,s)时带来较大困难。但发生渗透破坏可能存在一定的现象,如渗流量、渗水、散浸或浸润线等,所以渗流风险评价可结合现场检查情况作为分析依据。因此,为寻找简捷实用的大坝渗流风险定量评估方法,本模型以现场检查为主要方式,其分析方法如下:
土石坝渗透破坏主要有管涌、流土、接触冲刷和接触流土等多种形式。在进行渗透稳定评价时,通常采用出逸比降J大于临界比降JC作为判断依据,其风险率Pf2的数学表达式可构造为[5]:
Pf2=P(J>Jc)
(6)
式中:Pf2为渗透破坏风险;J为出逸比降;Jc为临界比降,Jc一般可通过原状土室内试验求得;在渗流破坏类型相互独立的假设下,则有:
Pf2=P1+P2+P3
(7)
式中:P1,P2,P3分别为发生管涌、流土和接触冲刷等破坏现象的风险率。
根据大量的经验数据,流土破坏的临界比降[6]的均值μJc可近似为1,考虑Jc为正态分布的前提下,则σJc=0.1。而对于出逸比降J,在坝体土质固定不变的情况下,只与上下游的水位差△H有关,故可将J写成[7]:
J=ξ△H
(8)
在△H固定的情况下,则J的均值μJc及方差σJc可写成:
μJ=△Hμξ;σJ=△Hσξ
(9)
其中ξ为不确定系数,取决于随机的自然地质地基条件、土力学计算模式的不完善性,如对各种渗控措施下渗径L、铺盖厚度T的简化计算。显然,μξ、σξ只随渗流的边界条件和地质条件变化,而不随ΔH变化,μξ一般可根据地质分布图,粗略给定,而σξ的确定就较为困难,要作专门率定。
在J和Jc为正态分布的条件下,可知[8]:
(10)
式中:β2为可靠指标,服从N(0,1)标准正态分布,因此:
Pf=1-Φ(β)
(11)
根据统计理论,若坝脚全长为L,若以10 m划分为一个独立段,则大坝可划分为0.1L段。在△H时,下游坝脚出现Li个险情点,则有理由认为[5]:
Pf=P{J≥Jc/ΔH}=0.1Li/L
(12)
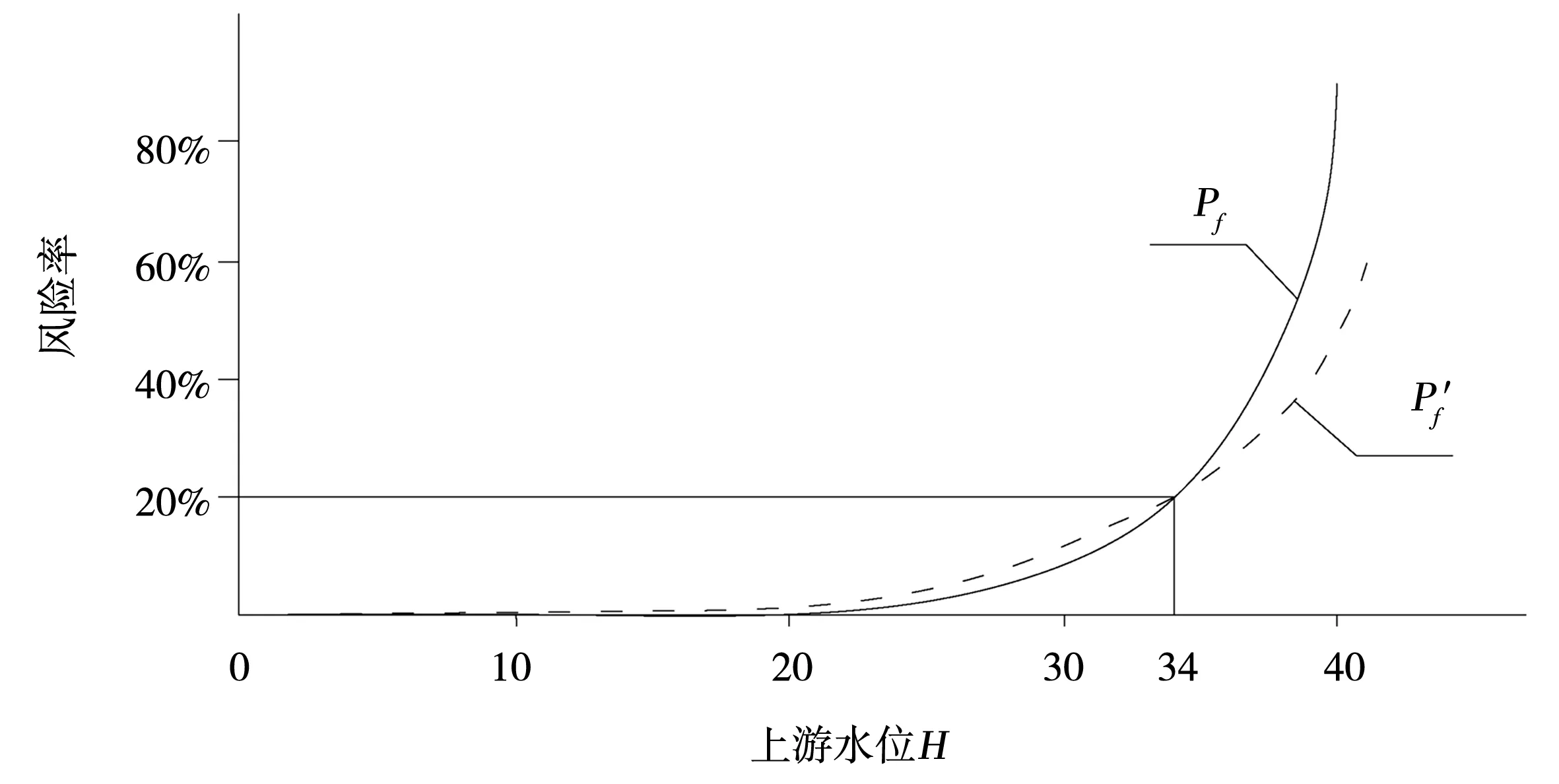
结合式(10)-式(12),只要能确定一点Pf(ΔH),就可算出β2,进一步反求σJ和σξ,可根据式(8)确定不同ΔH条件下的β2和Pf,从而整条ΔH~Pf曲线,见图2。

图2 渗流风险概率曲线图
模型计算方法的改进:以上所计算的渗流风险模型是以上下游水位差ΔH作为因变量,在短时间下,采用该模型是可行的。由于风险只与库水位有关,随着时间的推移,坝体土质结构很可能发生改变,渗流场发生变化,浸润线可能会抬高或降低,风险计算的指标出逸坡降也随之发生变化,风险率也随之发生变化。此外,若仍采用原模型进行以上下游水位差作为自变化,则有失准确。
另外,对于存在渗流监测设施来说,监测数据更能直接反映出渗流场的分布,在求取出逸坡降时更准确。因此,以监测数据作为分析对象,能够建立监测数据与风险分析成果相联系。
3 实例分析
3.1 工程概况
大余县水库工程管理局管辖的4座土石坝,分别为油罗口水库(大Ⅱ型)、跃进水库(中型)、石门口水库(小Ⅰ型)、合江水库(小Ⅰ型),水库均位于赣江支流章江河水系,座落在大余县的东北方向及西南方向,最大直线距离约40 km。
3.2 滑坡失稳风险分析
安全系数以毕肖普方法为依据,为便于分析,主要考虑正常工况及非正常工况:①正常蓄水位时对应的下游水位;②最高洪水位时对应的下游水位。有关参数参照安全鉴定报告或初设报告等,具体见表2。
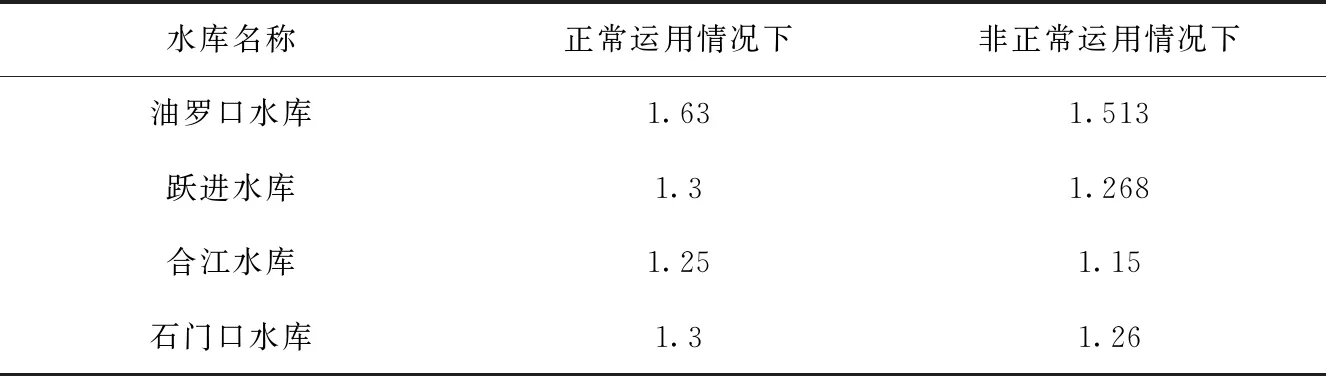
表2 不同工况下的安全系数
将各水库的参数代入,计算结果见表3。
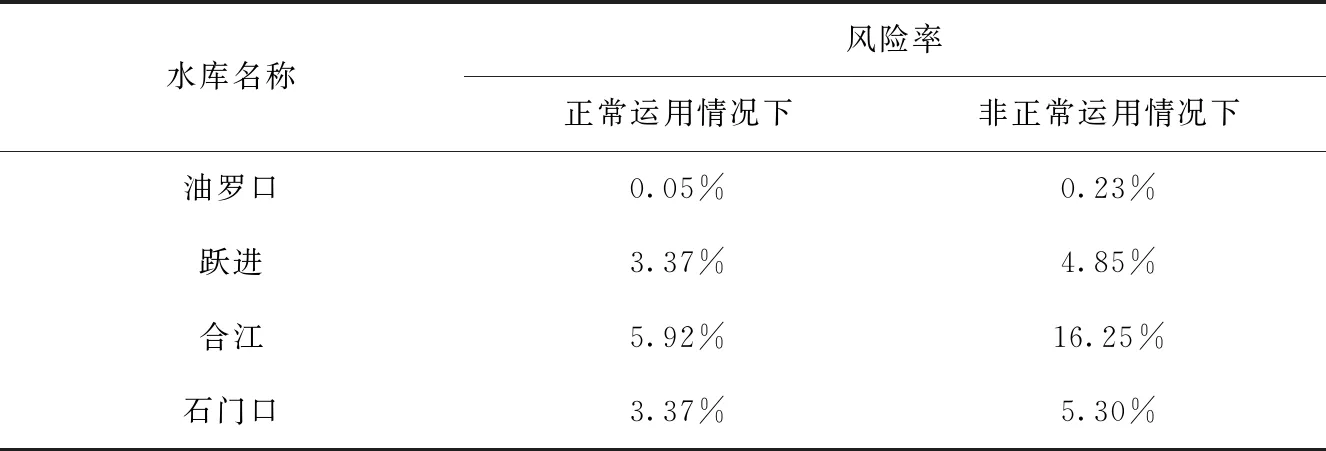
表3 不同工况下的风险率
根据计算结果可知,对于油罗口水库,风险率最低,在校核洪水位下,风险率为0.23%,而在正常蓄水位下,风险率仅为0.05%。而对于中小型水库,由于其安全系数较低,风险率偏高。如合江水库,在校核洪水位下,风险率达到16.25%。将风险率代入上式,便得各水库的年均风险率Pfi。
3.3 渗流稳定风险评价
鉴为篇幅有限,以油罗口水库为例,经现场检查发现,水位在250 m以上时,下游坝脚处出现1处湿润点。根据计算可知,J=0.63 图3 水库地质概化图 根据统计可知,Pf2=P{J≥Jc/ΔH=34}=1/5=20%,即在库水位250 m时出现1处破坏点,概率为20%,则据式(10)~式(12)可算出β=0.84,取μJc=1、σJc=0.1,求得σJ=0.43,将计算所得的出逸比降作为均值,即μJ=0.63,进而求出μξ=0.018,σξ=0.013,这样Pf与ΔH的关系就确定下来了。 图4 基于测压管水位数据的风险率曲线 水库风险分析是风险管理的基础,也是水利学者们关注的热点。本文从概率论的角度出发,探讨了风险计算方法,建立了土石坝边坡失稳、渗透破坏风险等相关计算模型,并结合有关规程规范,计算了不同坝高下的风险率,划定了不同大坝运行安全等级下的漫顶风险率分区图;分别计算了大余县4座水库的风险值,并对其分区进行了评价,风险结论与实际情况相符。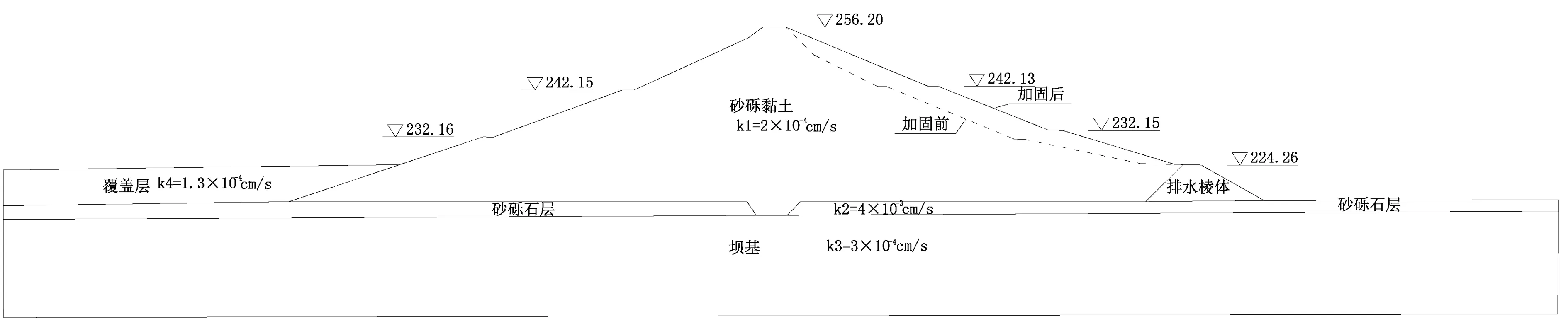
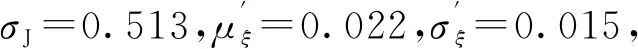
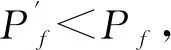
4 结 论
