基于FA-IACS算法的车辆路径问题优化*

刘巍巍， 孙宇彤， 安小宇， 高鑫禹， 孙晨曦

(1. 沈阳工业大学 机械工程学院， 沈阳 110870； 2. 郑州轻工业大学 电气信息工程学院， 郑州 450002)

车辆路径问题(vehicle routing problem，VRP)是Dantzing和Razmer在1959年提出的一个典型NP难问题[1]，一般通过启发式算法和精确算法来进行求解.启发式算法具有效率高、求解精度高的特点，相比之下，精确算法效率较低且通常只有在问题规模较小时才能获得精确解.现如今，学者们的研究重点主要放在启发式算法上，包括蚁群算法、遗传算法、人工神经网络算法、粒子群算法、模拟退火算法等.蚁群算法具有在解决车辆路径问题方面较强的全局搜索能力和较大的算法改进弹性优势，但传统蚁群系统(ant colony system，ACS)算法在寻优过程中存在过早收敛、容易陷入局部最优，且收敛到全局最优要花费较长时间等缺点[2].因此，探寻一种改进的ACS算法，使其能够同时提高VRP问题的求解速度和求解质量具有重要意义.

近年来，国内外许多专家学者提出了不同的改进方案以使蚁群算法更适配于VRP问题.Kao等[3]针对蚁群算法求解VRP时信息素停滞问题，混合蚁群算法和粒子群算法在蚁群算法中嵌入了信息素干扰的方法，提高了算法准确性，但容易过早收敛；Huang等[4]为了避免蚁群算法陷入局部最优，使用角运动改进蚁群算法应用于应急服务救援车辆的路径规划，并进一步使用经典ACS的转移概率选择规则的路径权重矩阵，以提高路径搜索的准确性，但该算法较为复杂且导致计算耗时较长；胡立栓等[5]针对蚁群算法容易陷入局部最优的问题，引入局部迭代搜索方式使算法能保持解的多样性，能够跳出局部最优，并用以求解VRP问题.

本文针对蚁群算法的缺陷，提出了改进蚁群系统算法(firefly algorithm and improved ant colony system algorithm，FA-IACS)，将蚁群算法的启发函数因子进行改进，增强算法全局搜索速度；利用萤火虫算法的搜索方式在探寻解空间方面具有多样性这一特点，对萤火虫算法(firefly algorithm，FA)的种群初始化等部分进行改进，提出了一种新的编码方案来编码萤火虫的种群库.在算法最后加入信息素震荡程序，保障算法的可靠性.所提出的算法具有更高的效率，且能有效地避免算法陷入局部最优.

1 问题描述及数学模型的建立

VRP问题的基本约束模型，即有容量约束的车辆路径优化问题(capacitated vehicle routing problem，CVRP)，由一组具有非负需求的节点和一个拥有车队的中央仓库组成[6-7]，可以表示为G={V，E}.其中，顶点集V={v0，v1，…，vn}由中央仓库v0、n个顾客v1，v2，…，vn以及对称边集E={(vi，vj)vi，vj∈V}组成.由于CVRP问题需要考虑配送中心数量和车辆型号等很多因素[8]，为了便于研究，本文做出以下基本假设：1)所使用的车辆皆为具有已知容量Q的相同车辆；2)所有车辆以相同的恒定速度行驶；3)节点需求量已知；4)每个节点都有且仅有一辆车；5)每个节点的需求量不能超过车辆的配送容量.

目标函数是在满足车辆净需求和容量限制的同时，通过使用最少数量的车辆来求解最小行驶总距离.求解最小行驶总距离可表示为minZ.数学模型可表示为

(1)

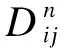
确保每辆车的最大载重量必须在车辆的限制(容量)范围内，其约束条件表达式为

(2)

式中：di为第i个节点的货物需求；Q为车辆的最大容量限制，为一个常数.

确保距离和使用时间不能超过车辆的最大允许距离，其约束条件表达式为

(3)

式中：tij为从节点i到节点j的运输时间；si为节点i的服务时间；T为车辆返回时间限制.

保证所有路径为闭合回路，即车辆由配送中心出发，回到配送中心，其约束条件表达式为

(4)

保证最多允许K条路线，其约束条件表达式为

(5)

如果车辆由节点i到节点j，则Xij为1，否则为0，其约束条件表达式为

(6)

2 FA-IACS算法设计

2.1 算法步骤

FA-IACS算法先进行初始化，并启动算法，对状态转移概率进行改进选择下一节点，直至客户集为空，进行萤火虫搜索，对萤火虫的编码方式进行改进，然后对信息素进行更新，在最小迭代次数时进行判断路径是否有优化，无优化则进行信息素震荡，否则，则继续算法迭代.算法流程如图1所示.

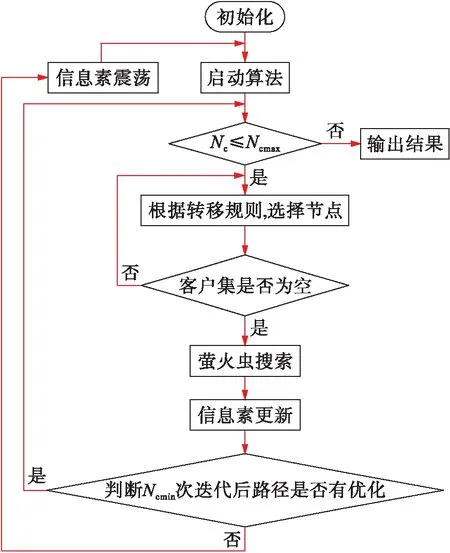
图1 FA-IACS算法流程Fig.1 Flow chart of FA-IACS algorithm

2.2 算法过程

算法运行前参数设定包括：蚁群算法的迭代次数Nc，最大迭代次数Ncmax，最小迭代次数Ncmin，当前最优解Gbest.

1) 启动算法

将“m”蚂蚁放在仓库中.设置Nc=1、Gbest=∞.对距离启发函数因子进行改进.

传统蚁群算法多采用当前节点i和下一节点j之间欧几里得距离的倒数作为启发函数因子，这种启发函数因子只是考虑了此刻节点与下一节点，而忽略了节点与目标节点之间的关系，因此会造成盲目路径搜索，致使搜索效率低和时间长等问题[9].在本文中，对启发式函数因子进行改进.将距离启发函数因子更改为下一个节点j和目标节点z之间的欧几里德距离的倒数.改进后蚂蚁路径搜索的过程中各节点距离目标节点越近，二者期望值越小，当当前节点可选择的下一节点与目标节点距离更近时，则期望值越大，其被选中的概率越大.这将有利于改进蚂蚁盲目搜索这一缺点，增强算法全局搜索能力和算法收敛速度.

改进的启发式函数因子表达式为

(7)

ηjz=1/d(j，z)

(8)

式中：j、z两点的坐标分别为(xj，yj)和(xz，yz)；d(j，z)为节点(j，z)的欧几里得距离.

2) 寻找路径

(9)

根据式(10)选择下一个要访问的节点，即

(10)

式中：τij为蚂蚁k在路径(i，j)上所释放的信息素含量；a为蚂蚁信息素启发因子，表示轨迹相对重要程度的参数；b为节点(i，j)间的转移期望启发因子，表示能见度的相对重要度的参数.每只蚂蚁附带清空表，每到达一个节点则清空客户集中该节点数据，当客户集为空时，则蚂蚁已访问过所有节点[10-11]，判断是否违反了车辆的容量限制，如果违反了则返回到仓库，并且开始规划新路线，如果没有则进行下一步骤.

3) 萤火虫搜索未开发解空间

蚁群算法中的蚁群会遵循信息素浓度，寻找信息素浓度较高的路径，导致ACS陷入局部最佳状态[12-14].因此，应用FA算法来搜索较少探索的其他有可能的区域.

由蚁群算法产生的“m”个解可以视为萤火虫的数量“m”.由于CVRP是最小化目标问题，因此，每个萤火虫的光强度设定为等于目标函数值的倒数.

根据光强度对“m”萤火虫进行分类.具有最小目标函数值的萤火虫即是最好的萤火虫，其他萤火虫对最佳萤火虫的吸引度β可视为光强度函数，其表达式为

(11)

式中：β为萤火虫之间的吸引度，吸引度与观察萤火虫所看到的光线成比例；β0为在r=0处的吸引度，r为萤火虫与光源的距离；rij为两个萤火虫之间的距离；γ为光吸收系数.萤火虫i向萤火虫j的运动xi可表示为

(12)

萤火虫的运动通过式(12)中给出的吸引度β和随机移动α的函数进行控制，α∈[0，1].

为了使FA适应离散优化问题，提出了一种新的方案来编码萤火虫.萤火虫编码为节点集合，FA指数代表节点访问序列号.“0”标志着新路线的开始，最后一个“0”表示整个过程的结束.以十节点为例，萤火虫编码方式如表1所示.

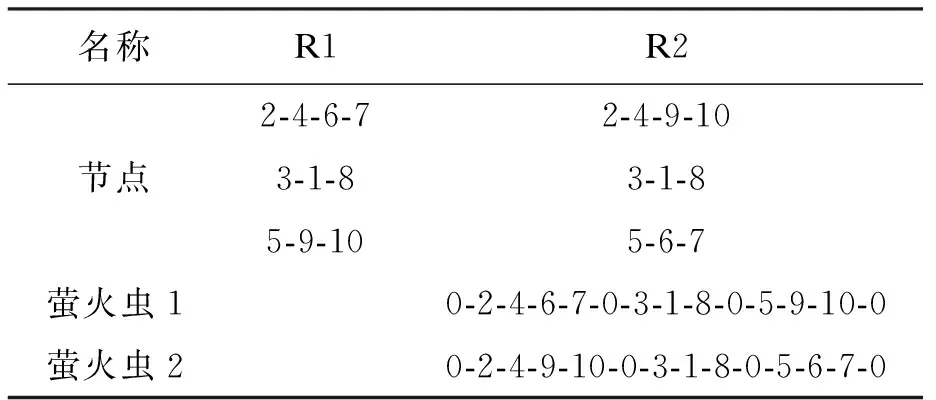
表1 萤火虫编码方式Tab.1 Firefly coding modes

定义两个萤火虫之间的距离rij为两个萤火虫之间由不同节点链接的链路总和，则表1中的rij为3(链路4-9，5-6以及6-7).

4) 返回到蚁群算法

在由FA搜索出的m解中，选择具有最小目标函数值的蚂蚁作为最优解，即Gbest.

5) 信息素更新

通过FA搜索出的最佳解决方案m用于更新Gbest和蚂蚁选择的最佳路径上的信息素浓度.蚂蚁可以在最佳路径上沉积信息素，用来引导后来的蚂蚁进行搜寻[15].此外，为了模仿天然蚂蚁，随着时间的推移，一些信息素会随之蒸发.因此，更新的信息素浓度τ′，其表达式为

(13)

(14)

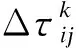
在最佳路径方案中存放的额外信息素为

(15)

式中，ξ为尾随的蚂蚁数量.

6) 信息素震荡程序

判断最小迭代次数Ncmin次迭代后路径是否有优化，如果迭代中没有改进路线，为了克服停滞不前的问题，提出了震荡程序以解决局部最优的问题.

震荡程序设置为更新边缘的信息素浓度，而不是更新解决方案中字符串，因为更新字符串可能会导致解决方案变为不可行解.震荡程序能够使蚂蚁探索新路线并避免选择相同的重复边缘.

7) 输出Gbest并停止.

3 仿真及结果分析

3.1 参数选取

为了全面验证所提出的FA-IACS算法的有效性，本文针对小规模标准算例1及大规模标准算例2两个案例问题进行了测试，将FA-IACS算法与标准ACS算法以及文献[5]中的改进蚁群算法(improved ant colony algorithm，IACA)组成了一个对比仿真实验.小规模标准算例1取自国际VRP算例库中经典案例，大规模标准算例2选取CVRP Set CMT算例集中的5个算例.仿真设备CPU为Intel Core 2 Duo CPU T6400 2.00 GHz 2 GHz，操作系统为Windows7旗舰版，开发环境为Matlab2014a.q0、a、b和ρ等参数值取自文献[16]，参数取值如表2所示.

表2 仿真参数Tab.2 Simulation parameters

3.2 小规模标准算例1

为了更好地比较算法之间性能，本文采用国际VRP算例库中经典案例中的E_n22_k4，E_n30_k3，E_n33_k4，E_n51_k5进行测试，时间单位为秒，仿真结果如表3所示.从表3中可以看出，FA-IACS算法在标准案例中算法仍具有较高的精度，对近似最优解的偏差率更低，准确性更高；而计算时间上该算法也大幅度地缩短了小规模案例计算时间，如算例E_n22_k4，本算法计算时间为15.45 s，与ACS的90.45 s，以及IACA算法的60 s相比具有更快的速度，证明了本文算法的高效性.图2为算例E_n22_k4中三种算法计算100次目标值的变化情况.从图2中可以看出，ACS算法得出的目标值较高，且稳定性较差，所得结果波动性较强，而本文算法目标值最低，且稳定性更好，波动幅度更低.

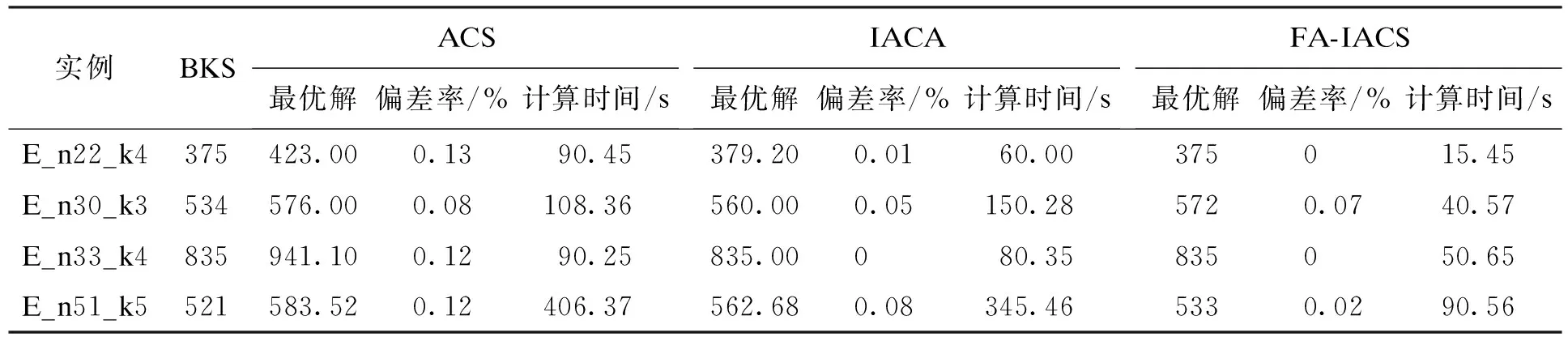
表3 标准算例1仿真结果分析Tab.3 Analysis of simulation results for standard examples 1

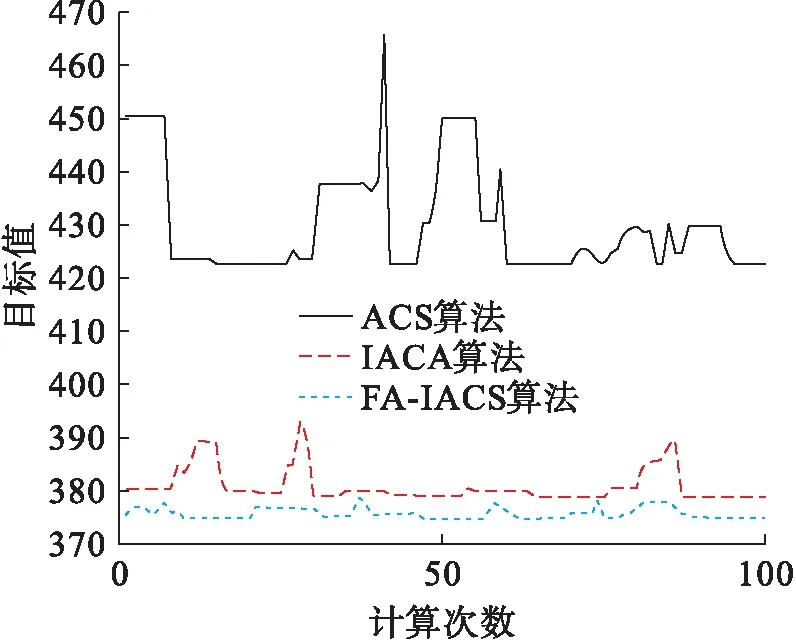
图2 E_n22_k4算例三种算法目标值对比Fig.2 Comparison of target values for E_n22_k4 example obtained with three algorithms

3.3 大规模标准算例2

为了验证本文所用算法在求解大规模VRP问题时的表现，选用选取CVRP Set CMT算例集中的5个算例.在查阅大量VRP问题研究后，发现大多文献所采用的问题规模属于小规模案例，并不能完全验证算法的有效性.因此，本实验选取具有较大规模节点的标准算例进行测试.实验结果如表4所示，时间单位为秒.从实验结果可以看出，本文算法在大规模案例中偏差率更低，最高偏差率仅为0.02%，计算时间也明显优于其他两种算法.

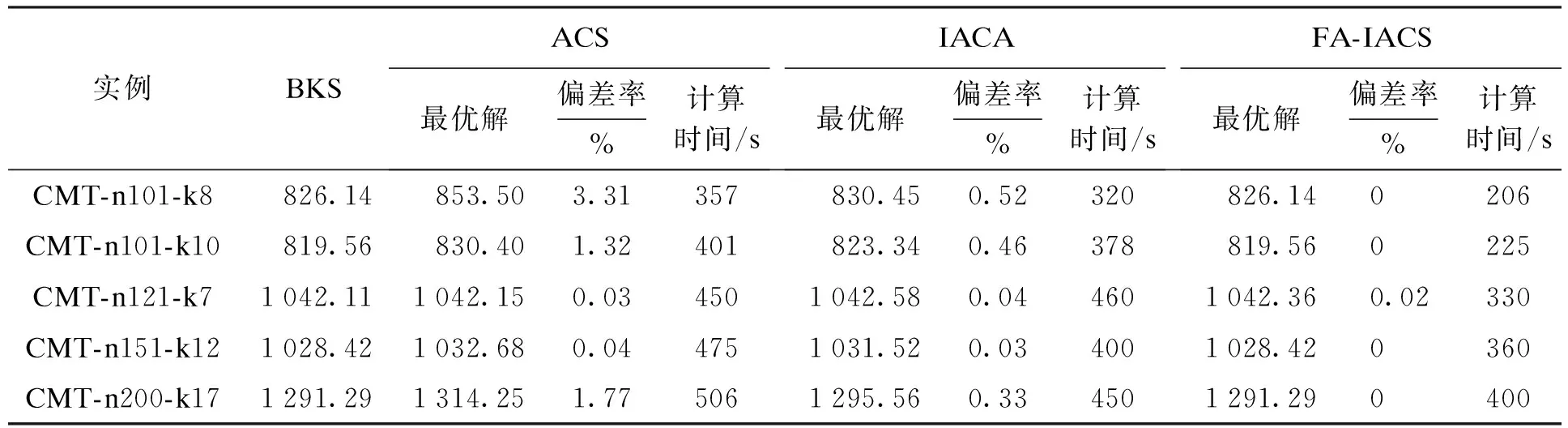
表4 标准算例2仿真结果分析Tab.4 Analysis of simulation results for standard examples 2

4 结 论

本文构建了一个可以更加有效求解VRP问题的FA-IACS算法，改进蚁群系统算法的状态转移概率，将蚁群系统算法与萤火虫算法的搜索机制相结合，改进萤火虫编码方式和距离测量技术，同时将蚂蚁路线上的信息素交换过程作为信息素震荡方案，使算法可靠性更高.通过小规模仿真实验可以看出，本文算法在解决方案质量和收敛速度方面要优于其他两种算法，通过大规模仿真实验可以看出，FA-IACS算法在大规模案例中表现也十分优秀.实验结果表明，本文算法在搜寻全局最优解、稳定性和收敛性上具有一定的优势.由于本文算法的参数是根据相关文献的经验值及实验测试值来确定的，采用单组参数对不同规模算例进行求解，对路径的随机性选择会产生一定的影响.