使用高频GPS 数据快速估计地震震级

徐拓

（上海市测绘院 上海200063）

1 引言

目前的地震预警系统主要基于地震仪/强震仪观测台网，利用仪器检测到的P 波(或/和S 波)进行地震参数估算，该方法对于中小地震非常适用。

但对于近场强震(MW>7)，由于地震仪/强震仪易受仪器倾斜、旋转等因素影响，积分后的速度和位移存在偏差，而且记录范围有限，基于地震仪/强震仪估计得到的震级将会出现饱和现象[1]。此时虽然仍能及时发布预警信息，但是不准确的地震震级在短时间内很难得到校正，严重影响预警实效。

为了解决上述问题，在地表位移监测中引入高频GPS 系统。其技术优势在于：(1)通过高频GPS 数据可以直接得到GPS 监测站的瞬间动态位移，不需要进行积分；(2)高频GPS 定位技术不存在振幅饱和问题，即使在(特)大地震时，也能够记录到较为准确的位移[1]。

文献[2]指出对于单个地震，同震地表最大位移(Peak Ground Displacement，PGD)的对数和震源距的对数之间存在比较明显的线性关系，给出式(1)和(2)：

其中，PGD 定义为三维时间序列上的最大位移，单位cm；R 为震源距，单位km；MW为矩震级；A、B、C为回归参数。Crowell 等给出的结果为A=-5.013，B=1.219，C=-0.178，按式 (3) 估计震级的中误差为MW0.224，即：

文献[3]通过处理总计10 个震级在MW5.3～MW9.1的地震的1Hz GPS 数据，得到1321 个台站的同震PGD，并采用L1 最小范数法求式(2)的回归系数。随后为了计算回归系数值的误差，随机移动10%的PGD 后重新进行回归计算，重复1000 次并估计回归系数的方差，结果为A=-4.4340.141，B=1.0470.022，C=-0.1380.003，按式 (4) 估计震级的中误差为MW0.27，有式(4)，结果如图1。

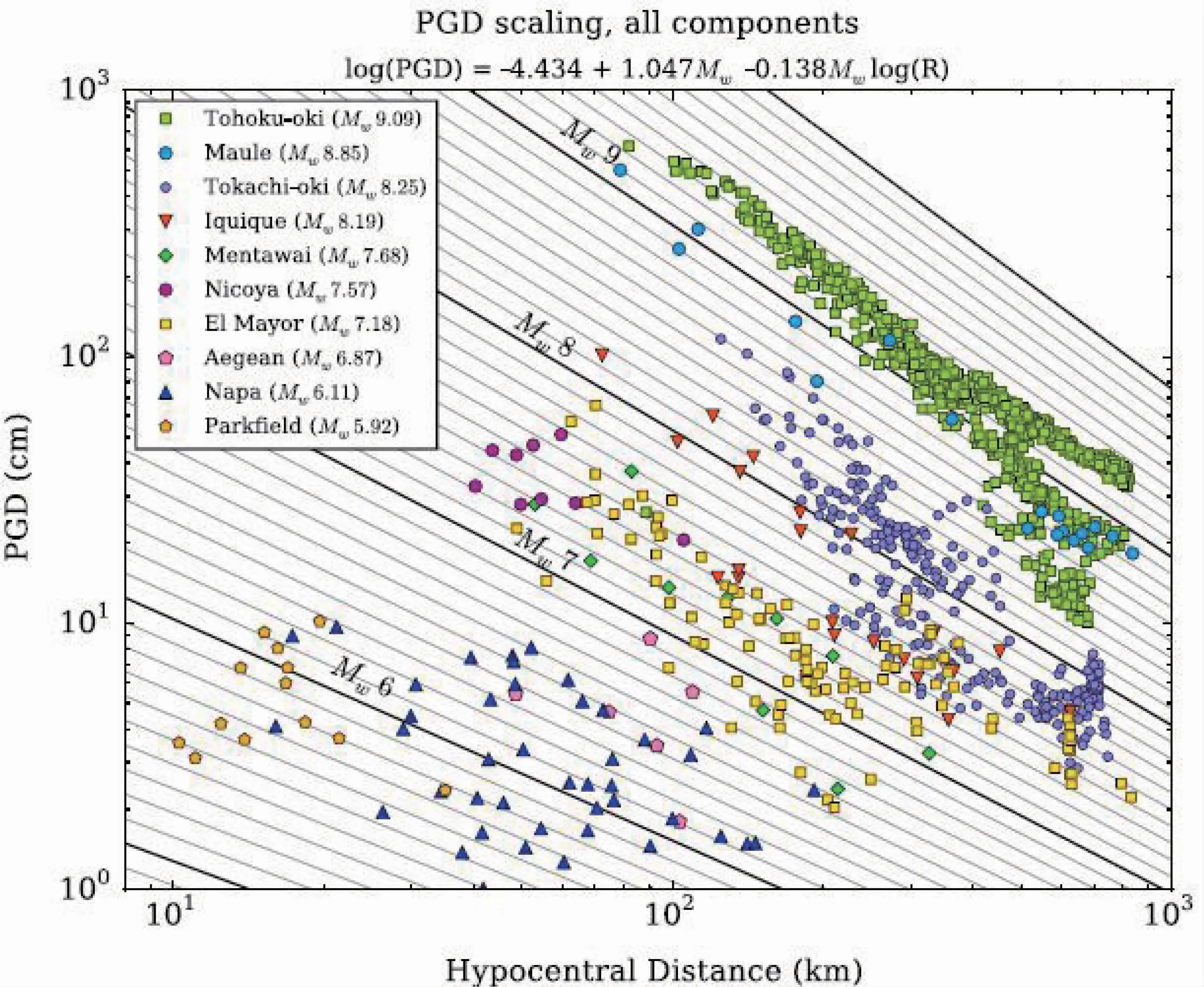
图1 PGD 与R 的回归关系图

在实际震级预警过程中，基本不可能使用震源距数百公里远的流动站观测值来进行震级预警，图1 中的地震除了日本东北地震因为发生在海域，离岸边最近的GPS 测站也有100km 左右的距离，导致震源距都偏大以外，其余地震事件都有震源距较小的观测站，因此笔者认为不需要考虑震源距过大的GPS 站的最大位移值，可以只使用震源距较小的GPS 测站的R-PGD 数据进行回归计算得到矩震级、震源距和PGD 之间的关系。

本文围绕基于高频GPS 数据进行快速震级估计开展研究工作，研究内容包括：(1) 使用GAMIT track 模块处理同震高频GPS 数据获取PGD，采用式(4)计算估计震级，并对结果进行分析；(2)根据解算的PGD 进行回归方程参数拟合，并通过模拟地震事件发生分析其精度。

2 基于高频GPS 提取PGD

通过解算日本东北(Tohoku-oki)MW9.1 地震、日本熊本(Kumamoto)MW7.0 地震，以及意大利诺尔恰(Norcia)MW6.6 地震的同震高频GPS 数据，提取PGD并根据式(4)计算估计震级。方法步骤如下：

（1）收集上述地震的震源参数、对应的同震近场高频GPS 观测数据；

（2）选择震源距大的参考站，避免共模误差，使用GAMIT track 模块解算高频GPS 数据；

（3）以每个测站在地震发生前60s 的坐标平均值作为该站的初始坐标，用于计算PGD，随后根据式(4)计算估计震级。

所选用的3 次地震的震源参数及对应可用的高频GPS 站点数见表1，其中震源参数来自美国地质调查局(USGS)网站。

表1 所选3 次地震事件信息

计算后的估计震级成果如表2 及图2 所示，分析三个地震事件对应高频GPS 站PGD 和估计震级数据时，可以得出：

（1）所选GPS 站的震源距均小于300km，没有加入震源距较远的台站数据；

（2）对于日本东北地震，使用式(4)计算近场GPS站PGD 结果偏大，平均估计震级为MW9.30，与真实值MW9.09 相比有差距，但仍在式(4)的一倍中误差范围之内；

（3）对于日本熊本地震，平均估计震级与实际矩震级相差较小，但震源距与PGD 的线性关系不明显，点分布较为离散，其原因是该地震发生在陆地上且以某一或某几方向的破裂为主，导致该方向上的GPS 站的PGD 结果偏大；

（4）对于意大利诺尔恰地震，平均估计震级与实际矩震级相差小。

分析式(4)的数据来源，推测产生这种结果可能的原因是在计算回归参数时：

(1) 采用了2011 年日本东北地震中更多震源距较远(400km～800km)且PGD 偏小的GPS 站数据，因此在震源距100km～300km 的范围上估计震级结果相对偏大；

(2) 选用的地震事件对应区域的GPS 站中有部分PGD 值与震源距之间没有特别明显的线性关系，分布较为离散。

表2 所选3 次地震事件估计震级

图2 所选3 次地震事件震源距R 与PGD 关系图，黑色斜线是式(4)预测的震源距与PGD 值关系曲线

3 模拟退火法计算回归参数

根据第2 节的同震PGD 结果，使用模拟退火(Simulated Annealing，SA)方法，解算式(2)中的回归参数A、B、C。进行1000 次并行运算，选择RMSE 最小的一组回归参数作为最优解，结果为A=-4.8350.110，B=1.0870.018，C=-0.1290.002，估计震级的中误差为0.25，代入式(2)有回归方程如式(5)。

lg(PGD)=-4.835+1.087·Mw-0.129·Mw·lg(R) (5)

从表3 和图3 的结果来看，式(5)对日本东北地震的GPS 站R-PGD 关系拟合较好，绿色点的线性关系明显，基本分布在代表MW9.1 直线上及附近，估计震级平均值为MW9.10，非常接近实际值；对日本熊本地震的GPS 站R-PGD 关系拟合效果一般，蓝色点分布较离散，线性趋势并不明显，估计震级平均值为MW6.96；对诺尔恰地震R-PGD 关系拟合的不错，估计震级平均值为MW6.64。

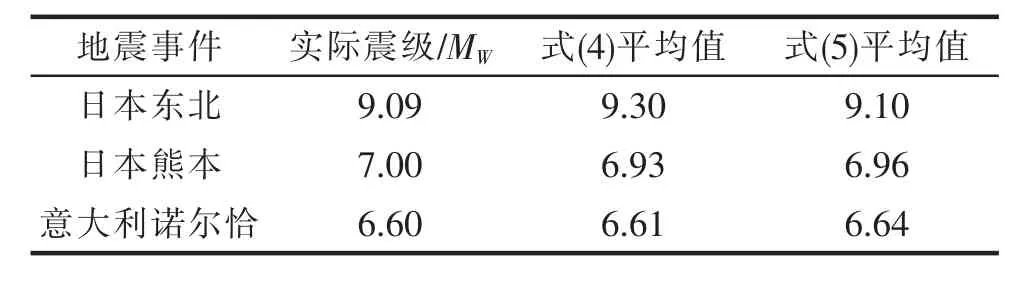
表3 所选3 次地震事件估计震级的平均值

图3 所选3 次地震事件震源距R 与PGD 关系图，黑色斜线是式(5)预测的震源距与PGD 值关系曲线

4 PGD 快速估计震级精度检测

使用2016 年11 月13 日新西兰MW7.8 地震的同震高频GPS 数据，模拟实际地震事件发生时快速估计震级过程，对式(5)进行精度测试。

利用PGD 估计震级不需要已知震源机制，只需要得到地震台网给出的震源经纬度和深度即可。实际中地震预警系统会采用4～6 台地震仪的P 波到时实时定位震源参数，所需时间与地震仪分布有关[4]。文献[5]基于Quake-Catcher 网检测2010 年新西兰达尔菲尔德地震余震，平均约9.1s 即可发布预警信息。地震发生在UTC 时间2016 年11 月13 日11：02：56，震中位于新西兰南岛中部城市安伯利(Amberley)东北54km 处，采用USGS 发布的震源参数：地震震中位置42.737°S，173.054°E，震源深度15.1km。

本次计算使用的1Hz GPS 数据来自新西兰土地信息GPS 活动控制网(LINZ PositioNZ)。剔除震时数据严重缺失和观测数据质量较差的测站后，以新西兰最北端的ktia 站(震源距855.34km)作为参考站，为模拟实际地震事件发生时震级预警过程，采用超快速预报星历igu，以及GAMIT trackRT 模拟实时高频GPS 解算结果，并假定已得到震源经纬度和深度，计算各站PGD 值，然后采用式(4)、(5)计算估计震级，以估计震级平均值作为实时预警震级结果。

4.1 快速震级估计结果

选择PGD 较大的测站作为示例站，分别是：震源西南方的hanm 站，以及震源东北方的kaik 站、trwh 站、wgtn 站、bthl 站、paek 站。

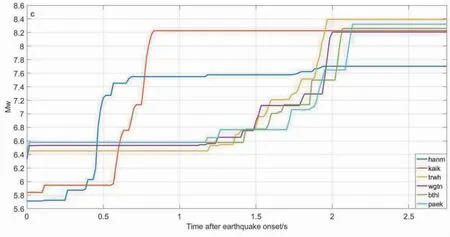
图4 使用式(5)计算的示例站PGD 估计震级收敛过程

图4 显示了震后30s，距离震源最近的hanm 站即已受地震影响，初始估计震级为MW7.27；震后50s，hanm 和kaik 站估计震级初步收敛，分别为MW7.55 和MW8.23，此时其他4 个示例站尚未受到地震波影响。震后150s，所有示例站估计震级均已收敛，震源东北方的GPS 站估计震级远超西南方，显示地震破裂方向主要沿东北向。

4.2 两种震级估计方程结果对比

表4 和图5 是式(4)与式(5)的估计震级结果对比。此次新西兰地震震源距R≤100km 范围内仅有4个高频GPS 观测站(hanm、kaik、lkta、yald)，两式对这4 个站的拟合效果均不理想，这与地震主要破裂沿东北方向有关，导致震源东北方向的kaik 站PGD 过大，两式得到的估计震级分别为MW8.3、MW8.23；而震源西南方向的lkta 站和yald 站的PGD 较小，估计震级仅为MW7.31、MW7.3 和MW7.44、MW7.41，均超出两式给出的估计震级误差。

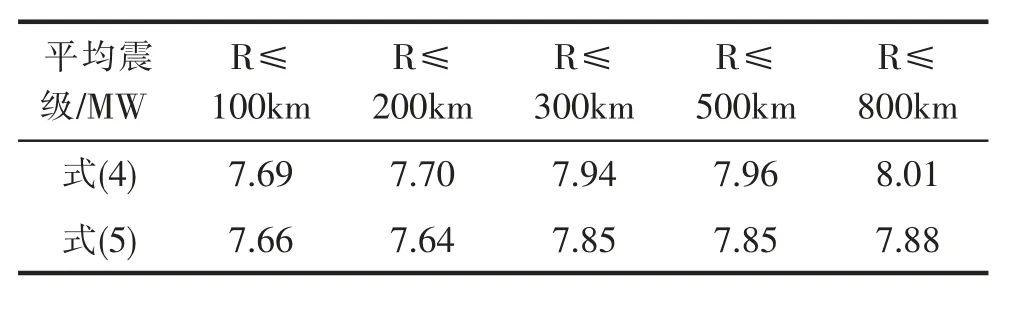
表4 一定震源距范围内GPS 站的平均估计震级

图5 基于式(4)、(5)的GPS 台站数与预警震级曲线

在R≤200km 部分，式(4)和(5)结果接近，均在误差范围之内。在200km≤R≤300km 部分总共有9 个流动站，其中6 个在震源东北方向，使得R≤300km部分的平均估计震级增大。在R≤500km 范围内，式(5)的平均值为MW7.85，式(4)的平均估计震级大于式(5)。

模拟此次新西兰MW7.8 级地震的快速震级估计结果表明，在震源距R≤200km 部分，本文用模拟退火法求出的式(5)结果与Melgar 等给出的式(4)结果基本一致；在R≥200km 部分，式(5)的结果要好于式(4)。

5 结论

本文利用模拟退火算法拟合PGD、震源距R 和矩震级之间的回归模型，结果为式(5)，随后通过实际地震事件模拟震后的快速震级估计。结果显示，该方法可用于快速估计地震震级，在震源距小于200km范围内，式(5)估计震级误差略大于式(4)；在震源距大于200km 范围，式(5)结果最接近实际值，二者都在误差范围之内。

本文所采用的PGD、震源距R 和矩震级之间的回归模型针对通用情况，在进行实际地震事件分析时未能考虑其震源机制、地质构造和断层机制。如果能针对某一地震多发区域，考虑其断层机制，研究适用于该区域的回归模型，则预警震级的精度会大大提高。