非量测数码相机三种检校方法的适用性评价

谷晴晴，李浩，丁影，宋美杰，胡龄心

(河海大学 地球科学与工程学院，南京 211100)

0 引言

近年来，随着无人机的快速发展和日渐成熟，无人机测绘技术在地形图绘制和城市三维建模等方面得到了广泛应用。然而，由于无人机自身体积小、载荷轻的特点，大多搭载的是非量测数码相机来完成拍摄工作。非量测数码相机凭借其成本低、重量轻、使用灵活方便等优势被广泛使用，但同时也存在着内方位元素未知、光学畸变差较大等缺陷，严重影响了摄影测量工作的精度[1-4]。相机检校技术可得到相机的内方位元素和畸变系数，恢复正确的光束形状，进而提高地形图测绘和实景三维建模的精度[5-7]。目前，相机检校的方法有很多，但通常在实用性和精度2方面很难兼得，在实际应用中应综合考虑工作条件、成本高低、精度需求等因素来选择一个合适的检校方法。常用的相机检校方法大体上可以分为2类：基于控制场的相机检校和无需控制场的相机检校。本文对3种基于控制场的典型检校方法展开研究，它们分别是基于三维控制场的光线束相机检校方法、基于二/三维控制场的联合运用透视变换和空间后方交会的相机检校方法(calibration method based on perspective transform and resection，PTR)，以及基于二维控制场的张正友标定方法。本文首先对3种方法的检校计算稳定性展开实验；然后对它们进行了量测应用精度的比较；最后对这3种检校方法从检校稳定性、量测应用精度和控制场布设难易方面进行了适用性评价分析，为以后相机检校方法在实际应用中的合理选择及保障无人机测绘质量提供参考和帮助。

1 3种检校方法的原理

1.1 三维光线束检校方法

光线束检校方法以共线条件方程式为基本数学模型，将像点坐标作为观测值，把内外方位元素、畸变参数、控制点的物方坐标等都作为未知参数进行整体平差。当考虑构像畸变差[8]时，其通常包括镜头的径向畸变和切向畸变。

另外，在平差过程中，对于控制点物方坐标还需添加一组虚拟观测方程，其有助于算法的收敛[9]，保证算法的有效进行。建立误差方程式后，采用最小二乘方法即可求解。

1.2 PTR检校方法

PTR是联合运用透视变换和空间后方交会进行相机检校的一种方法，将普通数码相机的畸变系数和内方位元素分别在二维、三维控制场中进行检校，以减弱2类参数之间相关性的影响，获得良好的检校效果[10-11]。该方法将畸变系数和内方位元素的计算置于一个处理系统中，二者进行交替解算，最终求得内方位元素与畸变系数的检校结果。

与光束法相机检校相比，PTR中的交替解算有利于消除诸多未知参数间相关性的影响，并且平面间的透视变换有利于表达构像畸变差影响。

1.3 张正友相机标定方法

1998年，张正友[12]提出了一种介于传统标定法和自标定法之间的基于平面模板的相机标定方法。该方法利用相机线性成像模型求解相机参数的初值，然后利用目标函数的非线性模型得到最优的相机参数[13]。该方法标定过程简单，避免了传统方法需要大型高精度控制场的要求，因此被广泛使用。其具体内容和操作参考文献[12]。

2 实验条件

本文实验使用的相机型号为FUJIFILMX-T10数码相机，分辨率为4 896像素×3 264像素。在拍摄照片时，将摄影方式设置为手动曝光方式，物镜对焦在无穷远处，从而锁定主距，即锁定了内方位元素值和物镜畸变系数。本文中利用的室内精密三维控制场、二维平面格网控制场以及二维棋盘格微型控制场如图1所示。

图1 控制场

室内精密三维控制场尺寸为3 600 mm×2 400 mm×2 000 mm，沿摄影方向分为前中后3个层面，最前面一层的控制点个数为49 个，后面两层均为35 个控制点，均匀对称分布在整个三维控制场中。二维平面格网控制场通过在特殊加工的硬质平板上绘制方格网而生成，格网数目为12 格×18 格，每格100 mm×100 mm，在格网线交叉点中选择47 个点，作为二维格网控制场的控制点。采用电脑程序生成7×14的黑白棋盘格，大小为20 mm×20 mm，角点数量共98 个，使其布满整个屏幕，作为二维棋盘格微型控制场。

3 检校计算稳定性分析

检校计算稳定性指的是当控制条件正常变动时，解算出来的参数应该稳定[14]，它是一种评价相机检校方法适用性的重要指标。

3.1 光束法

实验以室内三维控制场为摄影对象。首先，在其正前方架设中间摄站；然后，在距此摄站左边0.2 m处架设一个摄站；同样地，在距中间摄站右边0.2 m、0.4 m处分别架设另外2个摄站，总基线长度为0.6 m左右。4 个摄站距离控制场第一层约2.9 m，总共拍摄4张像片，使控制场影像均匀充满整个画幅，边缘不可留出太多的空白，保证所摄像片中控制点均清晰可见，尽量无遮挡，然后分别利用2张、3张和4张像片进行光束法解算。实验给出了4种控制点组合：组合一属于控制点共面的情况，利用了控制场第一层上的23 个控制点，它们基本处于同一平面，并且均匀分布；组合二和组合三属于控制点较少和较多的情况，分别利用了控制场3个层面上的23 个控制点和54 个控制点，它们均位于控制场的边角位置，在不同深度上数量相当，在同一平面上的分布均匀对称；组合四属于控制点稠密的情况，利用了控制场中的98 个控制点。用以上4种控制点组合进行实验，得到的内方位元素如表1所示。

表1 3种方案下的内方位元素

由表1可以看出，组合一和组合二之间f的偏差在3种方案下分别达到了48 个像素、8 个像素和20 个像素左右，虽然2种组合的控制点数量相同，但存在着是否共面的区别，内方位元素之间有较大的偏差。由此可见，光束法对控制条件的要求较高。对于控制点不共面的组合二和组合三，方案二和方案三的f的偏差分别约为7个像素和9 个像素，方案一中的偏差约为10 个像素。由此可见，控制点的数量和分布对检校结果也产生了较明显的影响。而对于控制条件良好的组合三和组合四，方案一的检校结果的最大偏差为2个像素，方案三的检校结果的最大偏差为1 个像素，而方案二的检校结果偏差更小，约为0.5 个像素，说明在控制条件良好的情况下，光束法的检校结果较为稳定。随着控制点个数的增加，3种方案解算出来的相机参数都逐渐达到稳定，但从整体上来看，方案二达到稳定的速度更快一些。

可以看出，光束法检校并不适合平面控制场，因此下节对有同样性质的PTR的后方交会不再测试控制点共面情况。

3.2 PTR方法

实验以二维平面格网控制场和室内三维控制场为摄影对象，摄站尽量设在2个控制场的正前方中轴线上，各拍摄一张像片，使控制场影像成对称分布，并使拍摄的像片中二维格网可以充满整个像幅，且各格网控制点清晰可见，便于量测，利用这2张像片便可以进行PTR的解算。为了比较PTR方法的稳定性，以不同的摄影距离对三维控制场拍摄了2张像片，从而使三维控制场上的控制点位置在这2张像片中发生了变化。其摄影距离分别为2.6 m和3.1 m，以这2种不同的摄影距离为根据得到2种实验方案，并对每种实验方案使用上述控制点组合当中的3种组合进行解算，得到的内方位元素如表2所示。

表2 2种方案下的内方位元素

由表2可以看出，2种方案下的组合二、组合三和组合四得到的相机参数最大偏差分别为4.5 个像素、3 个像素和2.5 个像素，表明在不同的摄影距离下PTR得出的检校结果是比较稳定的，并且随着控制点数量的增加，检校稳定性也随之提高。方案一下的组合二和组合三得到的相机参数最大偏差表现在像主点坐标y方向上，约为2.5 个像素，而方案二表现在像主距f方向上，约为5 个像素，与方案一相比稳定性较低，可能是由于控制场在影像中成像范围较小造成的。而对于组合三和组合四，方案一和二下得到的相机参数最大偏差均表现在像主距f方向上，分别约为3 个像素和2 个像素，说明在控制条件良好的情况下，PTR的检校结果是比较稳定的。总体上来看，在不同的控制条件下，PTR方法的检校计算稳定性表现较好。

3.3 张正友相机标定法

实验以电脑显示屏上的棋盘格影像为拍摄对象，对二维棋盘格的拍摄需保证整个显示器的成像在像片中不可太小，通过调整屏幕或相机的方向，拍摄一组不同位置和角度的像片，总共拍摄了32张像片。为了验证张正友标定法的稳定性，实验给出了2种方案。方案一利用这组像片中的少量、中量和大量像片来进行检校计算，其中少量像片是7张，中量像片是17张，大量像片是32张；方案二给出这组像片中2组数量相同但拍摄位置不同的15张像片来进行检校计算，得到的内方位元素如表3所示。

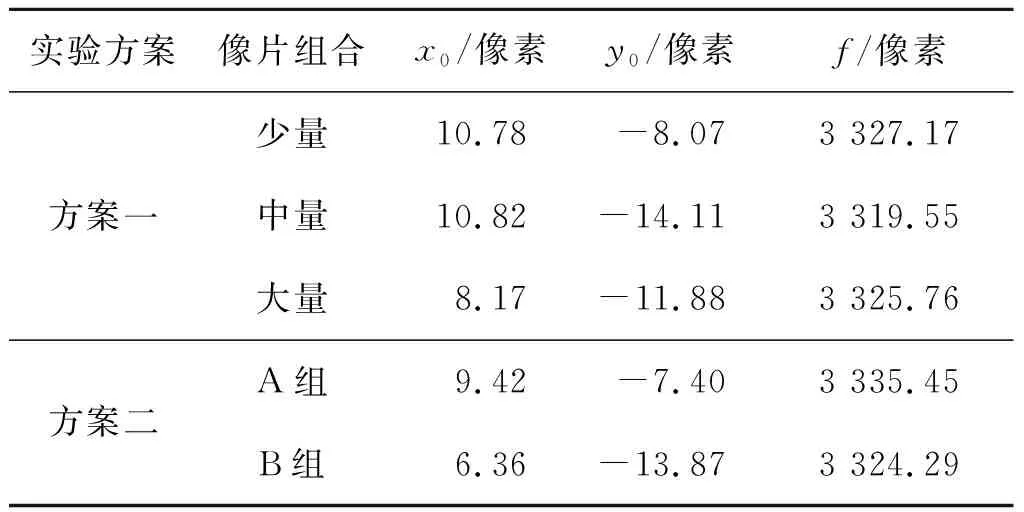
表3 2种方案下的内方位元素

由表3可以看出，方案一的像主距f的最大偏差在7.5 个像素，而像主点坐标x和y方向上的最大偏差分别为3 个像素和6 个像素。方案二的内方位元素的最大偏差表现在像主距f方向上，达到了11 个像素，另外，像主点坐标x和y方向上的偏差分别为3 个像素和6.5 个像素。由此可见，张正友标定法的检校计算稳定性受像片数量和姿态的影响较大。

4 量测应用精度的比较

在实际的测绘应用中，往往将相机预先检校得到内方位元素和畸变系数，然后作为量测型相机使用，利用检校获得的相机参数校正像点坐标，最后计算得到物方点位精度，即量测应用精度，它是衡量检校参数解算精度的实用标准。

实验以室内精密三维控制场为摄影对象，拍摄一个立体像对，利用3种检校方法得到的最佳相机参数，对像点坐标进行校正，然后使用摄影测量后方交会-前方交会量测算法，反算物方点位，得到检校参数的量测应用精度。选择控制场中的8 个点作为控制点，它们分布在3个层面上的边角位置，而其余的99 个点均作为检查点。应用后方交会-前方交会量测算法进行解算并求出坐标精度，物方坐标采用近景摄影测量坐标系，其X和Z方向分别沿水平和铅垂方向，Y方向与拍摄方向相同。为了避免量测结果的偶然性，对每一种方法得到的校正影像各量算2次，结果如表4所示。

表4 3种方法的量测应用精度比较

由表4可以看出，整体上来看，3种检校方法得到的中误差分布规律一致，均在Y方向较大，X方向最小，每种方法的2次计算结果基本上保持一致，解算较为稳定。通过表中的平均点位中误差可知，光束法与PTR方法的量测应用精度相当，均表现良好，而张正友标定法得到的精度比前二者略低些，但也可以满足中低精度的应用需求。

5 结束语

由于把所有的参数纳入到一个平差模型中进行解算，基于三维控制场的光线束相机检校方法会受到参数间相关性的影响，导致解算精度降低和不稳定，其稳定性在控制条件良好的情况下较好，否则欠佳。应用起伏不大的小型自动编码控制场，检校精度会受到限制，而布设高精度的三维控制场成本较高，灵活性较差。基于二维和三维控制场的PTR方法的量测应用精度跟光束法相当，且由于它分别在二维和三维控制场中解算相机畸变系数和内方位元素，采用分步检校逐次趋近的方法进行解算，可以有效地减弱解算参数之间的相关性，稳定性较好。与光束法和PTR相比，基于二维控制场的张正友相机标定方法精度略低，且稳定性受像片数量和姿态的影响较大。但此方法整个标定过程仅需要电脑上显示的棋盘格图像作为标定板，操作简单，携带方便，可做到灵活标定，大部分用户都可以利用此方法完成相机的检校，且可以满足中低精度要求的测绘应用需求。总之，在实际应用中，还需结合不同的工作环境、成本和精度需求等因素来合理选择相机检校方法。