大规模光伏发电配电网电压和无功协同控制的混合整数二阶锥规划方法

张庆晖，吴杰康，莫 超,3，吴 帆，唐惠玲，陈灵敏

(1.广东省城乡规划设计研究院，广州 510290；2.广东工业大学 自动化学院，广州 510006；3.南宁轨道交通集团有限责任公司，南宁 530029；4.广西博阳电力勘察设计有限公司，南宁 530028)

0 引 言

在分布式电源大规模接入的情况下，配电网无功功率平衡问题变得更复杂，使得电压控制变得更加困难。风力发电取决于风速，光伏发电取决于日照强度，而风速和日照强度均具有极大的不确定性，这使得风电机组出力和光伏发电系统输出功率也具有极大的不确定性。因此，风电大规模接入后配电网潮流变化更加频繁，电压控制变得更有难度[1-6]。

电压和无功协同控制一直是电网工作的重点，在新能源环境下，电压和无功协同控制受到高度重视。几十年来，国内外专家学者对电压和无功协同控制问题进行了深入研究，取得了许多研究成果。与传统配电网一样，分布式新能源配电网电压无功优化大多针对单目标进行优化，通常以网损或运行成本最小为目标函数[7-9]；有些采用多目标优化模型，目标函数除了网损、成本以外还包括有些技术指标和经济指标。目标函数的处理方法有许多，比如模糊集方法、权重法等[10-13]。对于配电网的电压无功优化问题，通常采用线性规划、非线性规划、动态规划、鲁棒规划、内点法等方法来求解[14-20]。

二阶锥规划是求解凸规划问题的一种数学方法，已在电力系统中得到应用。比如，采用锥规划方法，解决以网损最小化为目标函数、以无功源的无功功率为决策变量的配电网重构问题[21-22]、优化运行问题[23]。采用二阶锥规划方法，建立配电网有功和无功功率协调优化、无功源容量配置优化的混合整数二阶锥规划模型[24-25]，其核心技术是利用二阶锥规划理论对目标函数和约束条件函数进行线性化处理。

文中针对光伏发电大规模接入造成的电压质量问题，采用混合整数二阶锥规划方法，构建配电网电压和无功协同控制优化模型，验证其应用效果。

1 电压和无功协调控制优化模型

传统配电网中，有载调压变压器调压抽头调整与并联电容无功功率控制的协调性一直是一个难点，影响电压质量。光伏发电系统的大规模接入使得配电网无功控制的难度更大，除了要考虑有载调压变压器调压抽头的调整以及并联电容、静止无功补偿器无功功率的控制外，还要考虑静止无功发生器(SVG)、静止同步补偿器等先进无功补偿装置无功功率的调整控制以及分布式电源输出有功和无功功率的调整控制。

1.1 一般优化模型

在新能源环境下，配电网并联电容、静止无功发生器、静止同步补偿器无功功率的控制以及分布式电源输出有功和无功功率的调整控制需要协调性，其目标函数为在一个运行周期内网损最小：

式中：T为电压无功优化周期的时段数；Gij为支路i和j间的电导；Vi和Vj为t时刻节点i、j的电压值；θij为节点i、j的电压相位差；Δt为两个时段的时间间隔。

约束条件有：

1)系统潮流约束。节点注入功率要满足潮流方程：

式中：u(i)为与节点i相连的节点集合。

节点i注入有功功率等于光伏发电系统输出有功功率减去负荷有功功率；注入无功功率为光伏发电系统、SVG和并联电容器(CB)等输出的无功功率代数和减去负荷无功功率：

2)节点电压约束。节点i电压应不大于其允许的最大值，不小于其允许的最小值，节点i、j之间支路电流应不大于其允许的最大值：

式中：Vi、Vi.min和Vi.max分别为节点i电压实际值、允许的上限值和下限值；Iij、Iij.max分别为节点i、j之间支路电流实际值、允许的上限值。

3)并联电容器(CB)运行约束。并联电容器投入或切除的电容组数及电容容量制约条件为

式中：Qi.CB、Qi.CB.step分别为并联电容器投入或切除电容容量的实际值、一次允许投入或切除电容容量数值；Ni.CB、Ni.CB.max分别为并联电容器投入或切除的电容组数实际值、允许的上限值。

4)静止无功补偿装置运行约束。节点SVG输出无功功率应不大于其允许的最大值，不小于其允许的最小值：

Qi.SVG.min≤Qi.SVG≤Qi.SVG.max

5)分布式光伏电源运行约束。节点光伏发电系统输出有功和无功功率应不大于其允许的最大值：

1.2 混合整数二阶锥规划模型

将上述模型转化为混合整数二阶锥规划形式，二阶锥规划的标准形式为

式中：f(x)为具有线性或非线性组合的单目标或多目标函数；Ax=b为具有线性的等约束条件函数，x∈Rn，A∈Rm×n，b∈Rm；C为具有二阶锥特性的约束条件矩阵。

二阶锥：

旋转二阶锥：

引入如下中间变量：

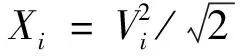
Yij=ViVjsinθij

Rij=ViVjcosθij

对电压和无功协调控制的一般优化模型的非线性目标函数和约束条件进行锥转化后得到二阶锥规划模型，其目标函数为

约束条件有：

1)系统潮流约束。节点注入功率要满足潮流方程：

2)系统安全运行约束。考虑中间变量，节点电压和支路电流应满足如下约束条件：

从以上约束条件函数中可以看出，部分变量和约束条件函数呈非线性，可以利用二阶锥对其进行线性化处理。经过二阶锥处理后可形成如下变量锥约束条件：

2 锥规划原对偶问题

二阶锥规划原问题模型：

mincTx+cf

s.t.lc≤Ax≤uc

lx≤x≤ux

x∈C

式中：lc和uc为线性约束的上下限；lx和ux为变量约束的上下限；x∈Rn，A∈Rm×n；C为二阶锥约束。

二阶锥：

旋转二阶锥：

二阶锥规划对偶问题模型为

对偶二阶锥：

对偶旋转二阶锥：

3 实例计算与分析

配电网中多为辐射式接线，现采用单馈线辐射式电路对混合整数二阶锥规划进行验证。分析在某一时间段内分布式光伏电源接入电网后，在混合整数二阶锥规划下的电压和无功协调控制，对无功补偿装置最优补偿容量能否进行合理选择。

在单馈线辐射式18节点的配电系统中，分别在3、4、7、8、9、15、16、17、18节点接入分布式光伏电源，这些节点的注入电网功率分别为2.5、1、3、2、6、5.5、3、5、3 MW。系统中安装有静止无功补偿器的负荷点有节点7和节点10，安装有无功补偿电容器的负荷节点有1、4、8、17节点，且每一组电容器的补偿容量为12 kvar。

通过混合整数二阶锥规划的计算后，得到各无功补偿节点的无功补偿容量分别如表1和表2所示。

表1 混合整数二阶锥规划下SVG补偿容量

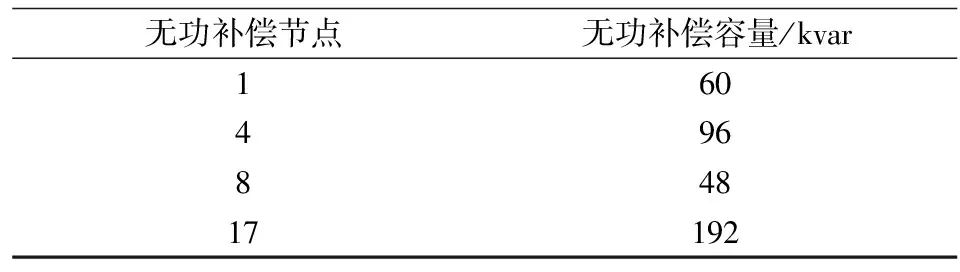
表2 混合整数二阶锥规划下并联电容器补偿容量

以1天为周期，将其分为24个时段，对多时段内的电压无功进行协调控制，作为连续型决策变量的静止无功发生器可以在一个周期内随着分布式光伏电源出力的变化和负荷的变动而动态地改变其无功补偿量，作为离散型决策变量的电容器在每个调度周期内允许操作的次数为6次。

在1个调度周期内，对电容器而言，将24个时间段分为6次动作时间，分别在5:00、9:00、13:00、17:00和21:00时进行动作。在21:00—5:00时间段内，光伏无出力，无功补偿装置不需要动作。分布式光伏电源接入后，根据混合整数二阶锥规划的无功补偿装置投切容量如图1和图2所示。

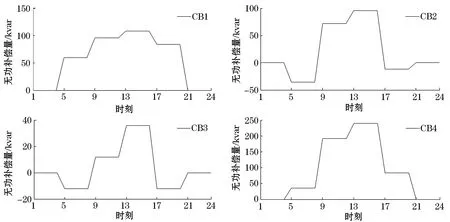
图1 无功补偿电容器动态优化投切策略

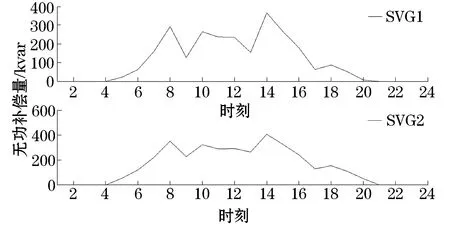
图2 SVG动态优化投切策略

在采用二阶锥规划的电压无功优化控制时，受电网拓扑结构的复杂性以及负荷节点数量、分布式光伏电源接入点和无功补偿装置安装地点的影响，二阶锥规划的电压无功优化控制的原问题不可行，此时可以通过将原问题转化为对偶问题求解，如图3所示。在此算例中，在采用二阶锥规划法分析某市10 kV配电网中接入分布式光伏电源时，考虑到馈线上负荷节点的数量、网络拓扑、无功补偿装置的安装地点和分布式光伏电源的接入点等原因，采用内点法求解过程中原问题会出现不可行的问题，所以此时将原问题转换为对偶问题，通过对偶解来求出原问题目标函数的解。

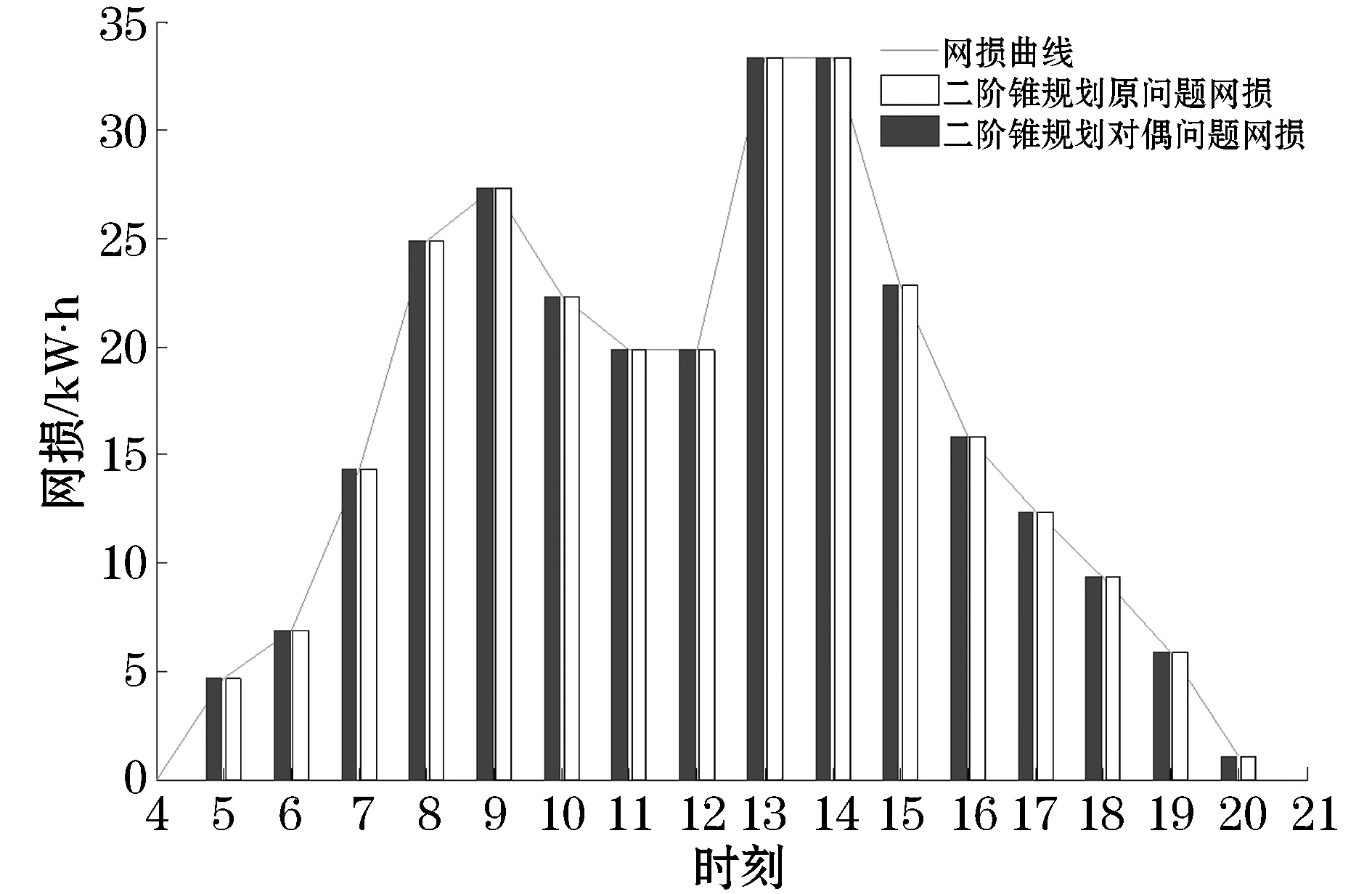
图3 二阶锥规划的原问题和对偶问题下的网损

4 结 语

1)光伏发电系统大规模接入使配电网电压变化更复杂，电压和无功协同控制也变得更加困难。利用原对偶问题的建模方法，通过构建电压和无功协同控制的锥规划模型，使控制模型更加简化，使求解更可行、更有效。

2)光伏电源、静止无功发生器和补偿电容器等协调运行，并协同控制其输出无功功率，可以实现新能源环境下配电网无功功率的优化平衡，保证电压质量。

3)采用内点法求解过程中原问题会出现不可行的问题，可以将原问题转换为对偶问题，通过对偶解来求出原问题目标函数的解。