全火星模型中震波传播特征的数值模拟研究

邓迪 肖万博 王彦宾

全火星模型中震波传播特征的数值模拟研究

邓迪 肖万博 王彦宾†

北京大学地球与空间科学学院地球物理学系, 北京 100871; †通信作者, E-mail: ybwang@pku.edu.cn

采用基于交错网格的傅里叶伪谱与有限差分混合方法, 求解弹性波动方程, 根据地球化学分析得到的两个火星理论结构模型, 模拟二维全火星模型中 P-SV 波和 SH 波的传播过程。根据理论地震图和波场快照, 讨论全火星模型中震波的传播过程以及各种震相的产生和演变, 分析模型内部火星壳厚度以及火星核幔边界深度对震波传播的影响。结果表明, 在低速火星壳内部多重反射波及转换波的相干叠加会形成很强的波列, 其特征受火星壳厚度的影响较大, 在切向分量上可以更清晰地观测到核幔边界的反射震相。

全火星模型; 震波传播; 数值模拟; 伪谱与有限差分混合方法

火星是太阳系中与地球有最多相似性的类地行星。研究火星的内部结构和物质组成, 对认识火星的形成和演化, 进而研究地球乃至太阳系的形成和演化历程具有非常重要的科学意义[1], 因此这也成为空间探测的重要研究课题。

地震波穿透性强, 对速度界面敏感, 具有较高的分辨能力, 普遍认为地震学是确定行星内部结构最好的地球物理学工具, 在地球内部结构研究中发挥着非常重要的作用。在美国阿波罗登月计划期间, 航天员在月球表面布设 4 台月震仪, 记录了大量月震数据。通过对这些数据的分析, 揭示了月球的内部结构特征[2]。

火星地震学的研究始于 1976 年美国的海盗计划, 但远不如月震探测成功。海盗 1 号着陆器于1976 年 7 月 20 日降落在火星上, 但是着陆器上的地震仪无法解锁, 没有任何数据返回。海盗 2 号着陆器于 1976 年 9 月 3 日登陆火星上的乌托邦平原, 着陆器上的地震仪连续工作 19 个月, 但除在第 80 个火星日记录到一个可能的火星震事件外, 没有其他发现[3]。该事件发生时, 没有记录到风数据, 因此不能排除风噪声的干扰。没有记录到其他事件的原因可能是地震仪在远震体波的频带宽度中灵敏性不足[4],也可能是由于仪器的位置导致其对风噪声的高灵敏度[5‒6]。

陨石撞击是引起行星内部震波传播的另一个潜在来源。在阿波罗计划 1969—1977 年对月球的 8年观测中, 4 个台站观测到 13000 多个月震事件, 其中包含约 1800 多个陨石撞击事件[7]。在月球上, 陨石直接落在月球表面并产生月震信号, 由于缺乏大气层, 因此仅通过表面位移就可以检测到所有的撞击。但是, 火星的大气层能非常有效地防止陨石撞击, 到达火星表面的 10kg 以下陨石的数量仅为入射到大气层陨石数量的 10%, 因此在火星上检测到陨石撞击的数量很少[3]。

对火星核结构的研究目前主要通过重力观测进行。Yoder 等[8]通过火星全球探勘者号(Mars Global Surveyor)的无线电跟踪分析, 测得火星太阳引力下的潮汐变形勒夫数2。观察得到的2值为 0.153± 0.017, 排除了火星核为固体铁芯的可能性, 至少外核是液体。之后, 研究人员对 2001 年火星奥德赛号(Mars Odyssey)、2003 年机遇号火星漫游车(Mars Exploration Rover Opportunity)和 2005 年火星勘测轨道飞行器计划(Mars Reconnaissance Orbiter)发回的跟踪数据进行一系列的分析, 确定2值为 0.169± 0.006[9‒10]。

Sohl 等[11]提出火星内部结构的两个模型, 他们在流体静力平衡和封闭传热的条件下进行求解, 得到质量、静水压力、重力、温度和热流密度的径向分布, 还获得火星模型的分层密度和火星震波速结构。两个模型分别是满足地球物理约束(即极惯性矩达到最大可能值)的模型 A 以及与来自火星的SNC 陨石的地球化学约束一致的模型 B。

2018 年 11 月 26 日, 洞察号火星地球物理探测器降落在埃律西昂平原, 并在火星表面部署地震实验仪器(Seismic Experiment for Internal Structure, SEIS), 用于研究火星内部结构。地震仪由长周期三轴宽频带仪和三轴短周期仪组成, 覆盖 0.01~50Hz 的频率范围。与海盗号地震仪相比, SEIS 检测火星震的分辨率有所提升。另一项与海盗号不同的重大改进是, 地震仪通过机械臂直接部署在火星表面, 并通过高效的隔热和隔风保护, 使其免受温度和风变化的影响。基于现有的火星知识, 预计 SEIS 每年可检测到几十次震中距 40°以内、矩震级大于 3级的火星震[12]。2019 年 4 月 23日, 法国国家空间研究中心(Centre National d’Etudes Spatiales, CNES)宣布洞察号首次在火星上检测到发生于 2019 年 4月 6 日的火星震信号。目前, 科学家仍在研究该火星震的数据, 以期确认其震源信息[13]。在洞察号发射之前, 针对可能观测到的火星震数据, 人们利用地震学方法开展了相关研究, 如火星震的活动性、火星震定位、震波传播、火星浅层结构和壳幔结构等, 为洞察号的设计与发射以及火星震观测数据的分析奠定了基础[14‒20]。

地震波数值模拟研究在地震学中起到非常重要的作用, 有助于理解复杂地震波的传播过程和解释地震观测数据。Furumura 等[21]将傅里叶伪谱法与有限差分法相结合, 对 1999 年台湾集集地震进行三维强震地面运动的数值模拟。马德堂等[22]运用傅里叶伪谱法与有限元法的混合方法, 对弹性波动方程进行求解。魏星等[23]运用傅里叶伪谱法与四阶精度有限差分方法的混合方法, 基于傅里叶伪谱法精度高、内存消耗少的前提, 发挥四阶精度有限差分方法对人工边界和自由界面的处理优势, 对二维模型进行弹性波场的数值模拟计算。秦艳芳等[24]将魏星等的方法推广到三维非均匀介质地震波传播模拟计算中, 在确保精度和效率的情况下, 成功地实现对三维沉积盆地模型的并行模拟计算。Wang等[25]和 Jiang 等[26]应用交错网格傅里叶伪谱法与有限差分法的混合方法求解弹性动力学方程, 分别模拟计算全月球模型中 P-SV 波和 SH 波的传播。

本文对二维全火星模型中火星震波传播进行数值模拟, 针对已有的理论火星结构模型, 模拟火星震波传播的理论地震图和波场快照, 讨论火星壳厚度和核幔边界深度对火星震波传播的影响, 可为解释未来可能获取的火星震数据以及火星结构和火星震发生机制的研究提供方法参考。

1 基于交错网格的傅里叶伪谱与有限差分混合方法和全火星模型

对于各向同性的弹性介质, 在柱坐标系(,,)下, 假设方向上所有变量保持不变, 在(,)平面内, 以速度和应力形式表示的 P-SV 波和 SH 波的二维波动方程为

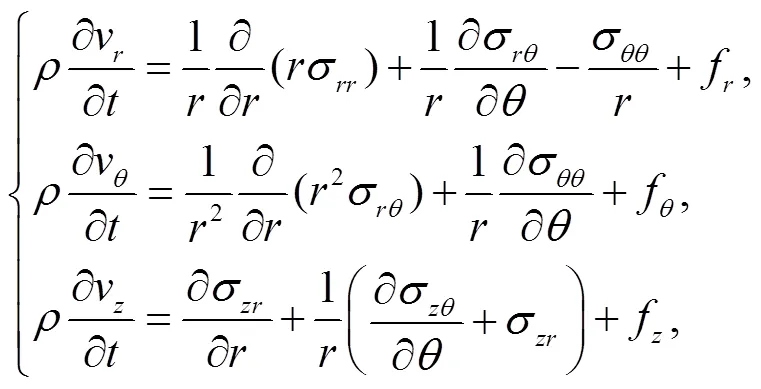
对于各向同性的弹性介质, 其本构关系为

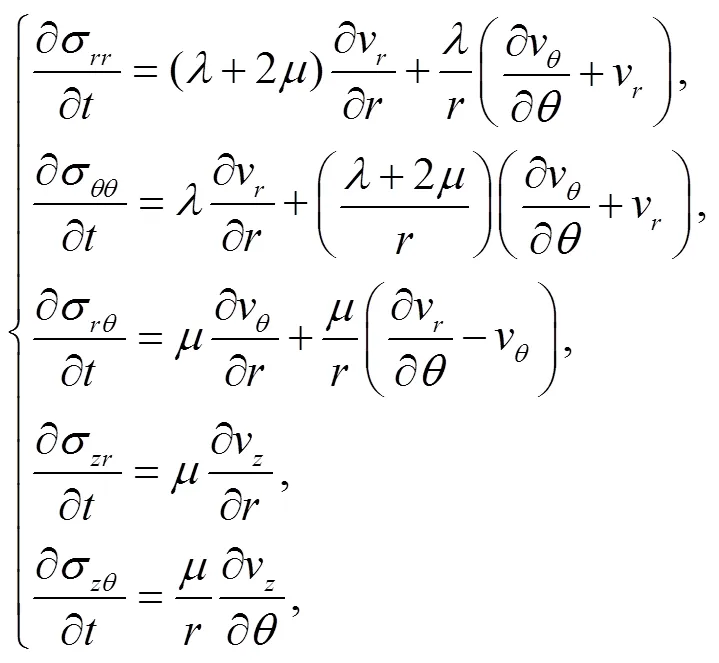
其中,v,v和v分别为垂向、径向和切向的速度分量,为介质密度,f,f和f分别为垂向、径向和切向的体力分量,,,,和为各应力张量的分量,和为拉梅常数。

本文中网格划分采用如图 1 所示的交错网格, 应力和速度分量在不同位置离散化, 彼此之间有半个网格间距。半径方向采用等间距网格离散化, 对于每个固定的半径, 横向网格点的数量是相同的, 横向网格的间距随着深度的增加而逐渐减小。采用基于交错网格的有限差分与傅里叶伪谱的混合方法, 对波动方程组进行求解。

在横向上, 通过傅里叶伪谱法计算空间变量对的偏导数[27]:

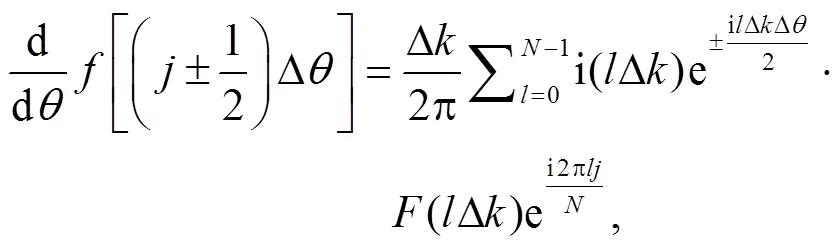
其中,=1, 2, …,–1,()表示在方向上离散的空间变量,()表示其相应的波数域的傅里叶变换,表示空间离散的网格节点数,和分别表示在方向上和波数域的离散间隔。

在半径方向上, 空间变量()对的偏导数由交错网格的四阶精度有限差分格式计算[28]:

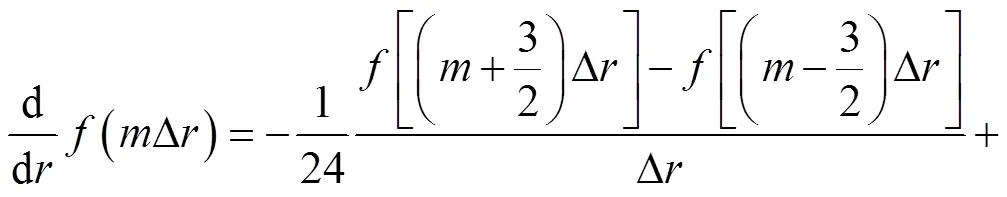
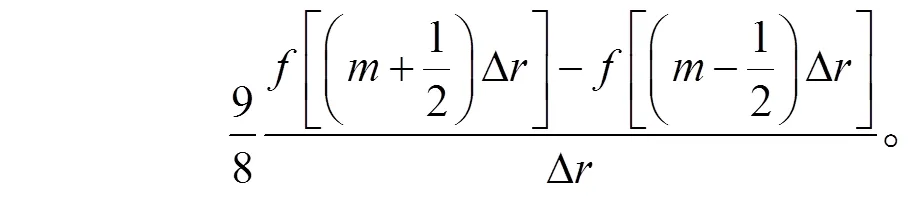
在模型区域内共需要处理两个边界条件, 通过满足表面处牵引力为零的自由边界条件, 将自由表面引入模型中。对于模型的中心区域, 采用 Cerjan等[29]提出的带有 20 个网格点的“缓冲区”的吸收边界条件。式(1)中的震源体力采用 Wang 等[30‒31]给出的二维柱坐标的线源形式:

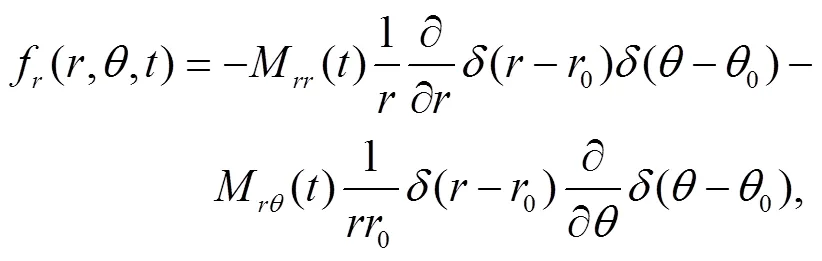
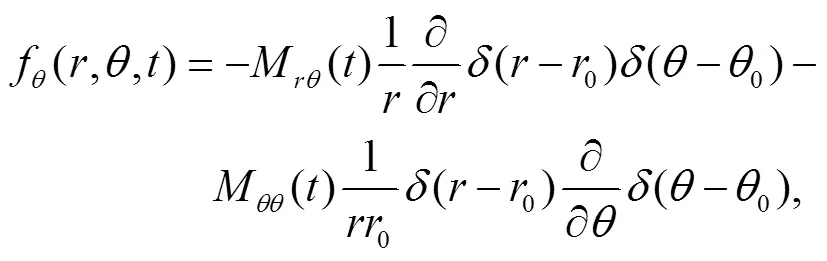
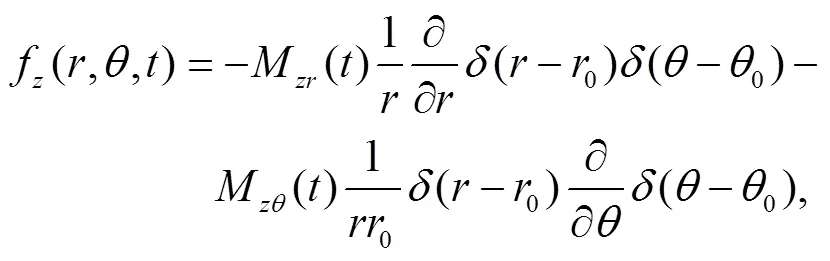
其中, (0,0)为震源中心位置;M,,,M和分别为震源矩张量的分量;()和()表示震源体力的空间分布方式, 采用 Herrmann[32]提出的伪函数进行近似计算。

本文选取以往研究中广泛采用的 Sohl 等[11]提出的火星内部结构参考模型 A 和模型 B, 两个模型的火星壳厚度分别为 110 和 250km, 火星幔上层与火星幔下层由橄榄石‒尖晶石过渡区分隔开, 火星幔下层又分为尖晶石层和尖晶石层两层。因此, 火星内部分为 5 层, 由浅至深分别是火星壳、火星幔上层(橄榄石层)、尖晶石层、尖晶石层和火星核, 各层的 P 波速度、S 波速度和密度分布如图 2所示。本文的值模型采用 Toyokuni 等[33]给出的值作为参考, 即液体核心内的值为 1000000, 其他区域的值均为600。

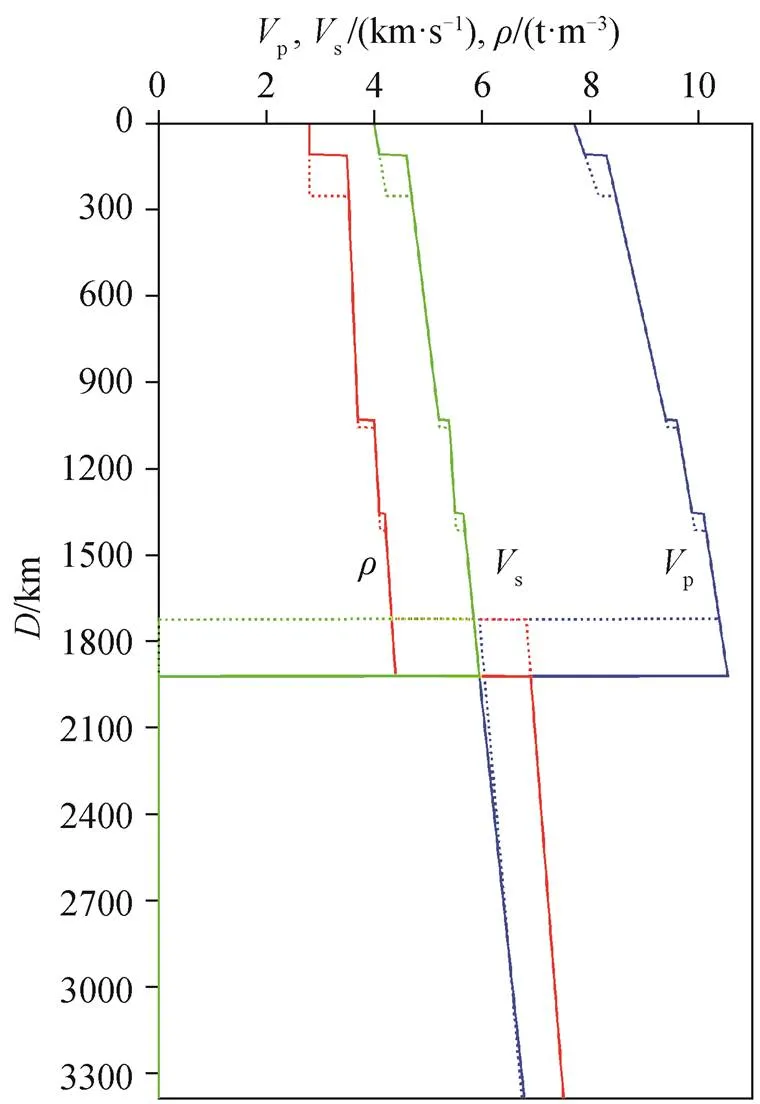
实线代表模型A, 虚线代表模型B

2 全火星模型的数值模拟

由于火星震的震源机制没有任何观测资料的约束, 本文在模拟过程中将典型的剪切地震震源作为参考。本研究的震源机制为二维双力偶线源, 取M= –1.0,M=1.0, M=M=0, 相当于一个 45°倾角的倾滑断层。模型的方向离散为 2048 个网格点, 范围为 0~2π;方向离散为 512 个网格点, 范围为0~3390km。因此,方向的网格间距为 6.62km,方向的网格间距最小为 0.02km, 最大为 10.40km, 位于火星模型表面。根据 Knapmeyer 等[34]构建的包含 13681 个火星震的目录, 火星震事件的震源深度最大可达 100km, 大多数事件的震源深度小于 60km, 因此本文模拟的震源深度为 60km。震源时间函数的宽度为 10s, 计算中使用的时间间隔∆由稳定性条件确定, 即受模型中最小网格间距∆min与最大波速max之比的约束。时间步长∆满足

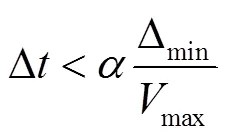
其中,为常系数0.26。中心附近的∆min为0.02km,max为10.5km/s, 因此得出的∆为0.0004s。该值在实际计算中过小, 因此需要设法加大∆。本文参考Wang等[30]提出的波数域滤波算法, 解决邻近球心=0处横向网格间距过小的问题。在计算横向导数时应用一个平滑因子, 即应用低通滤波器滤除高频波数成分, 由此得到的∆0.049, 比滤波前的时间步长提高约100倍。本研究取∆值为0.04s, 计算的总步数为75000, 能得到3000s的理论地震图。

在研究切向分量波传播时, 由于该分量上只有S 波, 且 S 波在火星液核内不传播, 因此对模拟参数做了调整, 将火星核内的网格点剔除。方向离散为 2048 个网格点, 范围为 0~2π;方向离散为 550个网格点, 范围为 1190~3390km, 因此方向的网格间距为 5.0km, 同时方向的网格能完整覆盖 SH波的传播路径。

2.1 模型 A 的理论地震图与波场快照

图 3 展示模型 A 在火星表面的合成理论地震图以及主要震相的理论射线到达时间, 可以看到, 由于火星核的存在, P 波传播到核幔边界时速度会明显减小, 并改变路径方向, 因此存在着直达 P 波的影区, 影区范围的大小与火星核半径有关。3 个分量上均能观测到互相对应的直达 S 波, 但只有径向和垂向分量能观测到直达 P 波, 同时能观测到 P 波的多重反射波 PP 和 PPP 等。径向和垂向分量上均能看到传播经过火星核的 PKP 震相, 只能看到很弱的入射到核幔边界发生反射的震相, 如 PcP, PcS 和ScP 等。切向分量上波形单一, 只能观测到 S 波, 多重反射波 SS 和 SSS 最为清晰明显, 同时能观测到 ScS, sScS, ScS2 和 ScS3 等核幔边界反射震相。由于模型 A 中火星壳厚度较小, 因此 ScS 和 sScS 震相的到时相差不大。在直达 S 波和 SS 波之间, 可以看到很强的低速火星壳内部产生的多重反射震相。同时可以看到, 3 个分量的理论地震图上面波均比较清晰明显, 径向和垂向分量上的振幅较大, 切向分量上的勒夫面波没有另外两个分量上的瑞利面波强。随着面波的传播, 波列越来越长, 频散现象越来越明显。

图 4 展示震源深度为 60km 的火星震激发的 P波和 SV 波在全火星模型 A 中传播的波场快照, 可以看到, 120s 时直达 P 波和 SV 波在火星幔上层向下传播, 具有清晰的波前, 同时能看到来自地表的直达 P 波和 SV 波的反射波和转换波, pP 和 sP 震相的波前依次在 P 波之后向下传播。在火星壳中, 速度比较慢的面波开始产生。在低速的火星壳中, 由于P 波和 SV 波的多重反射和转换作用, 形成直达波之后的较长波列。360s 时, 直达 SV 波到达核幔边界, 可以看到比较清晰的 P 和 pP 震相的核幔边界反射波, 面波和直达波之后多重反射和转换波的波列变得更强。420s 时, 来自核幔边界的直达 SV 波的反射波和转换 P 波向上传播, 由于 P 波影区的存在, 核幔边界附近可以看到弯曲的绕射 P 波。720s 时, 可以看到整个波场存在各种“Y”字形 P 波和 SV 波的多重反射波, P 波已经传播至火星核的另一面, 产生转换的 SV 波。

图 5 展示 SH 波在全火星模型 A 中传播的位移波场快照, 能够很清晰地看到直达 SH 波、多重反射 SS 和 SSS 震相以及传播到核幔边界反射的 ScS震相。180s 时, 直达 SH 波和经过表面反射的 SH波向下传播, 波场非常清晰。420s 时, 直达 SH 波到达核幔边界, 并产生反射SH波向上传播, ScS 和sScS 震相非常清晰。630s 时, 由于影区的存在, 核幔边界附近产生明显的绕射波。750s 时, 反射 SH波已传回地表, 能看到火星壳内传播的勒夫面波和低速火星壳内由于多重反射产生的很长的波列。

2.2 模型 B 的理论地震图与波形快照

图 6 展示模型 B 在火星表面的合成理论地震图以及各个主要震相的理论射线到达时间。与模型 A相比, 模型 B 的火星核半径更大, 因此直达 P 波的影区范围也更大。切向上, 由于火星核半径更大, 直达 SH 波的传播距离更短, ScS 震相的到时也比模型 A 更早。同时, 由于模型 B 的火星壳更厚, 低速区内 SH 波的传播距离更长, 因此 ScS 与 sScS 震相的到时相差更大。二次反射的 ScS2 震相和三次反射的 ScS3 震相等也是如此。由于切向上只有 SH波, 径向和垂向上 P 波和 SV 波会发生震相转换, 因此在切向上更容易估算波的传播距离和传播时间。

图 7 展示震源深度为 60km 的火星震激发的 P波和 SV 波在全火星模型 B 中传播的波场快照。180 s 时, 直达 P 波传播进入火星核, 比模型 A 更早。330s 时, 直达 SV 波到达核幔边界。360s 时, 由于模型 B 的火星核半径更大, 因此更早地产生弯曲的绕射波。900 s时, 波已传至另一侧火星表面, 可以看到很明显的多重反射震相。

图 8 展示 SH 波在全火星模型 B 中传播的位移波场快照。270s 时, 直达 SH 波到达火星幔上层与下层的分界面。由于模型 B 的火星壳更厚, 因此向下传播先经壳幔边界反射, 再经火星表面二次反射向下传播的 SmSS 和 sSmSS 震相与直达 SH 波和 sS波的距离更远。630s 时, 开始产生核幔边界绕射波。690s 时, 直达 SH 波经过核幔边界的反射波传回地表。

2.3 模型 A 与模型 B 理论地震图对比

为了讨论不同界面位置对火星震波传播的影响, 将模型 A 与模型 B 的理论地震图进行对比分析, 如图 9 所示。可以看出, 由于模型 A 的火星壳厚度更小, 低速区更薄, 因此直达 P 波的到时相对更早。震中距离较近时, 波形差异很小; 随着距离增加, 直达波的传播深度增加, 受火星壳幔速度结构的影响, 其波形与到时差稍有增加。多重反射震相受到的影响较大, 这是因为多重反射震相 PP, PPP, SS 和 SSS 等在传播过程中多次穿过低速的火星壳, 受火星壳厚度的影响很大。随着反射次数增加, 其到时差别越来越大。PcP 和 PKP 震相的到时均与火星核半径有关, P 波传播到火星核内之后速度变慢, 因此对于 PcP 震相, 火星核半径更大的模型 B 到时更早; 对于 PKP 震相, 火星核内传播路径更长的模型 B 到时更晚。同时, 模型 A 的面波频散要强一些, 面波的幅度更大, 持续时间更长, 面波更发育。切向上, 火星核半径更大, 直达 SH 波的传播距离更短, 模型 B 中 ScS 震相的到时也相对更早, 在图 9中能看到明显的差异。同时, 由于模型 B 的火星壳更厚, 因此 ScS 与 sScS 震相的到时相差也更大。与瑞利面波相比, 切向上勒夫面波的差异较小。

3 结论和讨论

本文采用基于交错网格的有限差分与傅里叶伪谱法的混合方法, 对目前广泛采用的两个全火星模型开展震波传播特征的数值模拟研究, 得到以下结论。

1)火星壳厚度对火星震波的传播起着重要的作用, 在低速火星壳内部, 多重反射波与转换波相干叠加会形成很强的波列。火星表面的多重反射波会多次经过低速的火星壳, 受火星壳厚度的影响很大。

2)核幔边界深度影响核幔边界反射波的到达时间和振幅。由于在切向分量上能够更清晰地观测到核幔边界反射震相, 因此利用切向分量记录到的核幔边界反射波可以更方便地进行核幔边界特征的研究。

3)通过对比模型 A 与模型 B 的波形图和波场快照, 可知模型 A 具有持续时间更长、频散更强的面波, 这与 Toyokuni 等[33]的结论相符, 即模型差异严重地影响面波的波列, 较薄的火星壳模型中面波的波列更长。

本文数值模拟的震源时间函数的主周期为 10 s, 在以后的研究中, 可以考虑不同的主周期, 进一步研究火星壳对不同成分面波传播的影响。模拟过程中采用的震源为二维线源, 与实际的三维点源相比, 由于存在波形和几何扩散的差异, 二者的模拟结果有差异, 可以利用二维线源到三维点源结果的转换进行近似的校正[30]。另外, 后续研究中可以尝试对火星震波在三维空间中的传播进行数值模拟, 并且讨论横向非均匀火星壳和地形变化对火星震波传播的影响。

[1] 欧阳自远, 肖福根. 火星探测的主要科学问题. 航天器环境工程, 2011, 28(3): 205‒217

[2] Lognonné P, Johnson C. Planetary seismology. Trea-tise on Geophysics, 2015, 10: 65–120

[3] Anderson D L, Miller W F, Latham G V, et al. Seis-mology on Mars. Journal of Geophysical Research, 1977, 82(28): 4524‒4546

[4] Goins N R, Lazarewicz A R. Martian seismicity. Geo-physical Research Letters, 1979, 6(4): 368‒370

[5] Nakamura Y, Anderson D L. Martian wind activity detected by a seismometer at Viking Lander 2 site. Geophysical Research Letters, 1979, 6(6): 499‒502

[6] Solomon S C, Anderson D L, Banerdt W B. Scientific rationale and requirements for a global seismic net-work on Mars [R]. LPI Tech. Rpt. 91-02. Houston: Lunar and Planetary Institute, 1991

[7] Nakamura Y. New identification of deep moonquakes in the Apollo lunar seismic data. Physics of the Earth and Planetary Interiors, 2003, 139: 197‒205

[8] Yoder C F, Konopliv A S, Yuan D N, et al. Fluid core size of Mars from detection of the Solar tide. Science, 2003, 300: 299‒230

[9] Konopliv A S, Asmar S W, Folkner W M, et al. Mars high resolution gravity fields from MRO, Mars sea-sonal gravity, and other dynamical parameters. Icarus, 2011, 211: 401‒428

[10] Konopliv A S, Park R S, Folkner W M. An improved JPL Mars gravity field and orientation from Mars orbiter and lander tracking data. Icarus, 2016, 274: 253‒260

[11] Sohl F, Spohn T. The interior structure of Mars: imp-lications from SNC meteorites. Journal of Geophysi-cal Research, 1997, 102: 1613‒1635

[12] Lognonné P, Banerdt W B, Giardini, et al. SEIS: insight’s seismic experiment for internal structure of Mars. Space Science Reviews, 2019, 215: 1‒170

[13] Brown D, Johnson A, Good A. NASA’s InSight Lander captures audio of first likely ‘Quake’ on Mars [EB/OL]. (2019‒04‒24) [2019‒05‒01]. https://www. nasa.gov/press-release/nasa-s-insight-lander-captures- audio-of-first-likely-quake-on-mars

[14] Clinton J F, Giardini D, Böse M, et al. The mars-quake service — building a Martian seismicity catalo-gue for InSight. Space Sci Rev, 2018, 214: 1‒33

[15] Knapmeyer-Endrun B, Ceylan S, van Driel M, Crustal S-wave velocity from apparent incidence angles: a case study in preparation for InSight. Space Sci Rev, 2018, 214: 1‒40

[16] Zheng Y, Nimmo F, Lay T. Seismological implications of a lithospheric low seismic velocity zone in Mars. Phys Earth Planet Inter, 2015, 240: 132–141

[17] Khan A, van Driel M, Böse M, et al. Single-station and single-event marsquake location and inversion for structure using synthetic Martian waveforms. Phys Earth Planet Inter, 2016, 258: 28–42

[18] Lognonné P, Karakostas F, Rolland L, et al. Modeling of atmospheric-coupled Rayleigh waves on planets with atmosphere: from Earth observation to Mars and Venus perspectives. J Acoust Soc Am, 2016, 140(2): 1447–1468

[19] Bissig F, Khan A, van Driel M, et al. On the detectability and use of normal modes for determining interior structure of Mars. Space Sci Rev, 2018, 214: 1‒28

[20] Bozdag E, Ruan Y, Metthez N, et al. Simulations of seismic wave propagation on Mars. Space Sci Rev, 2017, 211(1/2/3/4): 571–594

[21] Furumura T, Koketsu K, Wen K L. Parallel PSM/FDM hybrid simulation of ground motions from the 1999 Chi-Chi, Taiwan, earthquake. Pure and Applied Geo-physics, 2002, 159(9): 2133‒2146

[22] 马德堂, 朱光明. 有限元法与伪谱法混合求解弹性波动方程. 地球科学与环境学报, 2004, 26(1): 61‒64

[23] 魏星, 王彦宾, 陈晓非. 模拟地震波场的伪谱和高阶有限差分混合方法. 地震学报, 2010, 32(4): 392‒400

[24] 秦艳芳, 王彦宾. 地震波传播的三维伪谱和高阶有限差分混合方法并行模拟. 地震学报, 2012, 34(2): 147‒156

[25] Wang Y, Takenaka H, Jiang X, et al. Modelling two-dimensional global seismic wave propagation in a laterally heterogeneous whole-Moon model. Geophy-sical Journal International, 2013, 192(3): 1271‒1287

[26] Jiang X, Wang Y, Qin Y, et al. Global SH-wave pro-pagation in a 2D whole Moon model using the parallel hybrid PSM/FDM method. Earthquake Science, 2015, 28(3): 163‒174

[27] Witte D C, Richards P G. The pseudospectral method for simulating wave propagation. Computational Acoustics, 1990, 3: 1‒18

[28] Levander A R. Fourth-order finite-difference P-SV seismograms. Geophysics, 1988, 53(11): 1425‒1436

[29] Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations. Geophysics, 1985, 50(4): 705‒708

[30] Wang Y, Takenaka H, Furumura T. Modelling seismic wave propagation in a two-dimensional cylindrical whole-earth model using the pseudospectral method. Geophysical Journal International, 2001, 145(3): 689‒708

[31] Wang Y, Takenaka H. SH-wavefield simulation for a laterally heterogeneous whole-Earth model using the pseudospectral method. Science China Earth Scien-ces, 2011, 54(12): 1940‒1947

[32] Herrmann R B. SH-wave generation by dislocation source —a numerical study. Bulletin of the Seis-mological Society of America, 1979, 69: 1‒15

[33] Toyokuni G, Ishihara Y, Takenaka H. Preliminary modeling of global seismic wave propagation in the whole Mars // 42nd Lunar and Planetary Science Conference. Woodlands, 2011: Abstract no. 1631

[34] Knapmeyer M, Oberst J, Hauber E, et al. Working models for spatial distribution and level of Mars’ seis-micity. Journal of Geophysical Research, 2006, 111: 11006

Numerical Modeling of Global Seismic Wave Propagation in the Whole Mars Models

DENG Di, XIAO Wanbo, WANG Yanbin†

Department of Geophysics, School of Earth and Space Sciences, Peking University, Beijing 100871; † Corresponding author, E-mail: ybwang@pku.edu.cn

The pseudospectral and finite difference hybrid method on staggered grid is applied to solve seismic wave equations for two Martian structure models derived from geochemical analysis. The numerical modeling is used to calculate P-SV and SH wave propagation inside 2-D whole Mars models. The generation and propagation of various seismic phases in the whole Mars models are shown by synthetic seismograms and wavefield snapshots. Effect of Martian crustal thickness and the depth of Martian core-mantle boundary on seismic wave propagation is analyzed with synthetic seismograms. Multiple reflections and conversions of seismic waves and their constructive interference inside the low-velocity Martian crust form reverberating wave trains, which are strongly affected by the thickness of Martian crust. Seismic reflections from core-mantle boundary can be clearly identified from the calculated transverse component seismogram.

whole Mars model; seismic wave propagation; numerical modeling; pseudospectral and finite difference hybrid method

10.13209/j.0479-8023.2020.029

国家自然科学基金(41930103)资助

2019‒05‒16;

2019‒10‒13