永磁同步电机电磁噪声有限元分析
2020-07-29陈致初彭俊郭淑英李伟业
陈致初,彭俊,郭淑英,李伟业
(中车株洲电气技术与材料工程研究院,湖南株洲 412001)
0 引言
相比于传统异步电机,永磁同步电机在运行效率、转矩密度等方面性能均有明显优势,目前已在能源发电、工业制造及电力驱动等领域得到广泛的运用。在新能源汽车、城市轨道交通等对声环境敏感的应用领域,对噪声要求很高,需要在电机设计中优化降低电磁噪声,因此对电磁噪声准确计算方法的研究尤为重要。
国内外较早就开展了电机电磁噪声计算方法的研究,文献[1]采用解析法对异步电机、电励磁同步电机、直流电机等进行了电磁噪声的分析研究。文献[2]采用了ANSYS workbench对盘式电机的电磁噪声进行了分析研究。文献[3]、[4]采用专业软件对电机的电磁噪声进行了分析研究。本文采用电磁场有限元、声固耦合有限元相结合的计算方法,对永磁同步电机的电磁噪声进行仿真分析。
1 电磁噪声仿真分析流程
永磁同步电机电磁噪声仿真分析步骤包括建立电机二维电磁场有限元仿真模型,计算气隙中电磁径向力波的时空图谱,并对其进行二维傅里叶变换,得到径向力波的阶次和倍频数;建立电机定子与周围空气的声固耦合三维有限元仿真模型,加载径向力波载荷进行谐响应分析,后处理得到声压级分布,分析流程图见图1所示。

图1 电磁噪声仿真分析流程
2 二维电磁场有限元分析
电机二维电磁场有限元分析步骤包括单元类型选择、材料属性定义、二维建模、给各面赋予单元类型及材料属性、剖分生成有限元单元、求解及后处理、转子旋转处理等[5],其中定义的材料属性有硅钢片、永磁体、空气,二维建模是通过坐标系的变换,创建关键点、线、面及其布尔运算完成,剖分采用的四边形八节点网格,采用瞬态场计算,后处理中在电机气隙中间创建一条路径,按极坐标提取路径上的气隙磁密,包括径向磁密和切向磁密,然后根据式(1)计算气隙径向电磁力密度的值,将各时刻的气隙径向电磁力密度连起来就形成了气隙径向电磁力波。
(1)
式中,Bx—径向磁密;By—切向磁密;σ—力密度;μ0—真空绝对磁导率。
本文以槽极配合为488的永磁同步电机为例来进行二维电磁场有限元分析,得到其空载磁密云图见图2所示,空载力波时空图见图3所示,其中横轴为空间角度,纵轴为时间上的电机转子旋转电角度,将空载力波进行二维傅里叶分解,得到力波的阶次和频率的阶次(倍频),如图4所示。

图2 磁密分布云图

图3 力波时空图
为了便于分析,将0阶力波、8阶力波单独绘制成柱状图,如图5、图6所示。
从图5中可以看出,0阶力波中12倍频力波的幅值较大,其由1阶齿谐波所产生,由于一般电机定子的0阶模态固有频率比8阶模态固有频率低,0阶力波更容易与定子0阶模态固有频率重合产生共振,引起较大的电磁噪声,因此,0阶力波要加以关注。
从图6中可以看出,8阶力波中2倍频力波的幅值最大,其由基波磁场所产生,14倍频力波幅值次之,其由1阶齿谐波所产生。
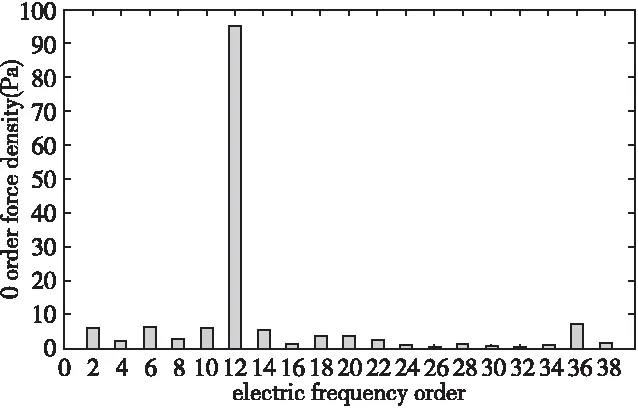
图5 0阶力波
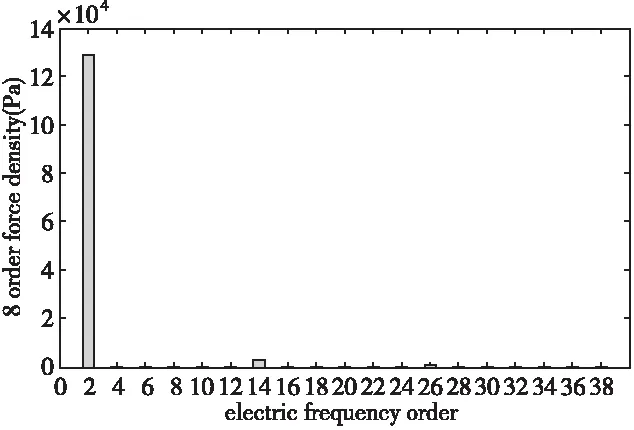
图6 8阶力波
3 三维声固耦合有限元分析
采用三维结构有限元单元Solid45对电机的定子部分进行建模,采用三维声固耦合单元FLUID30对电机定子周围的空气声场进行建模,以及采用与三维声固耦合单元FLUID30匹配使用的声场无穷远场单元FLUID130来模拟空气求解区域边界条件,具体仿真建模步骤如下。
3.1 实体建模
在三维声场有限元仿真中,要求无穷远边界圆的半径距离发声体的最小距离为0.2λ(λ为求解频率波长)[6],因此电机周围空气域的半径要满足与声波频率波长的关系。周围空气域采用球体建模,建立的三维实体模型见图7所示。

图7 三维实体模型
3.2 定义单元类型、实常数及材料属性
定子铁心采用的是硅钢片材料,机座采用的是铸铝材料,定义定子铁心、机座的单元类型均为Solid45,材料属性为弹性模量、泊松比、密度;定义与机座耦合的周围空气单元类型为FLUID30,以及不与机座耦合的周围空气单元类型为不具备自由度UX、UY、UZ的声场单元FLUID30,材料属性均为密度、声速;定义空气的边缘采用无穷远场单元FLUID130,并定义该单元的实常数,材料属性与空气相同。
3.3 有限元单元剖分
三维有限元剖分单元质量对有限元的求解的速度、精度影响很大,在本文中定子铁心、机座的剖分方式采用扫掠剖分,单元形状为6面体8节点,周围空气采用自由剖分,单元形状为4面体4节点。剖分之后的有限元模型见图8所示,其中,周围空气单元做了透明化的显示处理。
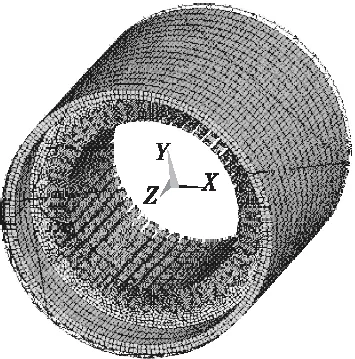
图8 三维有限元模型
3.4 声固边界耦合
在机座与空气接触的面上建立声固耦合,具体操作方法是选择机座表面的节点和与机座接触的空气单元,将二者的自由度UX、UY、UZ的进行耦合。耦合后的结果见图9所示,其中,红色为创建的节点与单元的耦合标识。

图9 声固节点单元耦合
3.5 修改非耦合空气单元类型
将不参与声固耦合的空气单元的单元类型修改为不具备自由度UX、UY、UZ的声场单元。
3.6 创建无穷远单元
选中空气域最外层的节点,在其上创建无穷远单元FLUID130,材料属性与空气相同。
3.7 施加约束
在电机机座两端面每隔90°的位置,选者节点定义其位移自由度UX、UY、UZ为0,作为结构计算的约束,这样约束与实际等效较为接近,约束后的结果见图10所示。
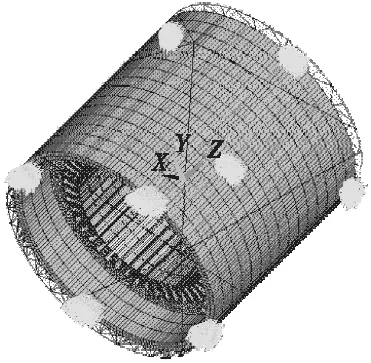
图10 约束条件
3.8 施加载荷
本文采用谐响应分析类型,在谐响应分析中可以加载多个力载荷,其中载荷的方向、幅值、相位可以不同,但载荷的频率必须相同,因此,需要逐一单独对二维电磁场有限元分析得到的气隙径向力波加载进行谐响应分析。为了将气隙径向力波加载到声固耦合三维有限元模型中,本文采取了如下措施:(1)以每个齿的齿顶面作为一个力的加载单元,该齿顶面上所有的节点力载荷具有相同的方向、幅值和相位;(2)所有齿顶面上力的方向均为径向;(3)所有齿顶面上力的幅值相等,其中该幅值为力波波形在齿距宽度内的平均值幅值;(4)所有齿顶面上力的相位根据力波阶数来计算。
例如0阶力波加载后的结果见图11所示,8阶力波加载后的结果如图12所示,其中红色箭头为加载力的标识。

图11 0阶力波加载

图12 8阶力波加载
3.9 求解及后处理
采用谐响应求解器进行求解,定义载荷频率,载荷频率即为力波频率[7],定义求解方法为完全法求解完成后,进入后处理,可以选中电机定子,绘制定子位移云图;可以在电机中间位置建立剖视图,绘制空气中的声压级云图。例如0阶定子位移云图如图13所示,0阶声压级云图如图14所示,8阶定子位移云图如图15所示,8阶声压级云图如图16所示。
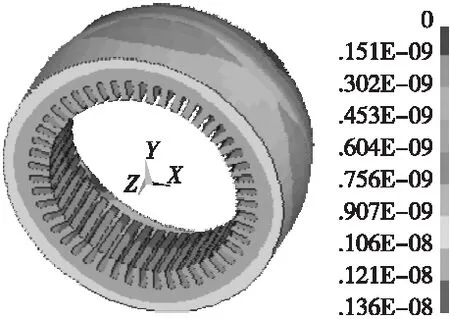
图13 0阶定子位移云图

图14 0阶声压级云图

图15 8阶定子位移云图

图16 8阶声压级云图
在后处理中除了绘制云图外,还可以得到空气中任一位置的声压级数据,根据声压级数据可以调整电机设计方案,对电磁噪声进行优化降低。
4 结语
本文提出了一种永磁同步电机电磁噪声有限元的计算方法,能计算得到电机周围空气中的声压级分布,对永磁同步电机电磁降噪工作具有较大的促进作用。
