基于时间权函数的落角约束导引律中剩余时间的估计方法
2020-07-29张友安赵贺伟
梁 勇,张友安,赵贺伟
(1. 海军航空大学岸防兵学院, 烟台 264001; 2. 烟台南山学院电气与电子工程系, 烟台 265713)
0 引言
随着战场目标对抗手段日益多样,对导弹的攻击要求也逐步增多。导弹在命中目标时,不仅希望获得最小脱靶量,还往往希望命中目标时导弹姿态最佳,以使战斗部发挥最大效能,取得最佳毁伤效果。在末制导约束中,通过线性二次最优控制理论可以得到满足落角和脱靶量约束的最优制导律[1-4]。针对这一问题,不少文献开展了相关研究[5-7]。针对垂直平面内的再入飞行器,文献[1]提出了一种控制落角约束的最优制导律;文献[2]提出了一种带落角约束的能量最优制导律设计;文献[3]提出了考虑终端速度约束的最优制导律,并且可以将速度约束直接转变成终端落角约束;文献[4]针对以不同的速度打击机动目标的情况研究了带落角控制的制导律,将该制导律与弹上预测目标位置跟踪器结合在一起;文献[5]和文献[6]针对任意阶常速导弹系统,得到了基于能量最优、落角约束的最优制导律的广义形式;文献[7]通过考虑与文献[2]一样的代价函数得到了一种最优制导律,并假设当前的加速度命令为剩余时间的线性形式,将零脱靶量和终端速度误差作为状态变量,通过将终端速度矫正到落角方向可以得到期望的终端落角;文献[8]针对落角和终端速度约束提出了最优制导律。上述制导律都是基于最优控制理论得到的,而文献[9]和文献[10]在比例导引律的基础上添加了控制落角约束的一个时变偏置项。对于静止目标,文献[11]的圆轨迹制导是偏置比例导引的另外一种形式,该制导律的主要思想是将导弹导引在导弹和目标之间的椭圆轨道上。尽管当N=3时比例导引律情况下能量是最优的,但是考虑初始位置或者角度存在误差、目标机动等外界干扰和不确定性的情况,在实际中N>3的情况是被应用于导弹系统中的[12]。注意到比例导引律的制导增益是和导弹和目标的能量比例相关的[13]。其他关于制导增益的解释可以参考文献[14]。
对于上述最优制导问题的闭环形式的解,需要知道准确的剩余时间[15],但是剩余时间又不能通过任何的装置来测量。最优制导律的性能取决于剩余时间估计的准确度,因此,需要一个比较可行的剩余时间估计算法。由于落角控制的弹道轨迹是比较弯曲的,所以传统的估计剩余时间的方法(距离除以速度)会产生很大的误差,尤其是导弹在末制导段的初始时刻。针对上述问题,本文通过建立导弹实际轨迹近似模型,提出了一种实用的剩余时间计算方法。
1 落角约束最优制导律设计
针对静止或者缓慢移动的目标,图1所示为末制导段几何关系。其中,Vm、θm和θmf分别表示导弹的速度、弹道倾角和期望的落角,am是垂直于导弹速度的法向加速度,通过控制输入u(t)来实现。

图1 规划航迹示意图Fig.1 Planned trajectory of the missile
如图1所示,导弹末制导阶段运动方程为
(1)
在假定Vm是常量和θm小角度的情况下,可以线性化方程式(1)。
定义
v(t)=Vmθm(t)
(2)
系统状态方程为
(3)
其中
(4)
(5)
最优控制问题为,寻找控制变量u(t)使得以下性能函数值最小
(6)
并且满足方程
Dx(tf)=E
(7)
其中
(8)
vf=Vmθmf,tf代表飞行时间,R是正的加权函数
(9)
剩余时间的定义为
tgo=tf-t0
(10)
当N=0时,问题就变成了文献 [5]中的纯能量最优控制问题。使用式(9)中的剩余时间加权函数,可以改变制导指令分布。对于N>0,当t→tf时代价函数逐渐增大,所以当t=tf时控制最后变成0。
通过对最优控制问题求解可以得到状态反馈解为
u*(t)=R-1BTFG-1(FTx(t)-E)
(11)
其中
(12)
将式(5)和式(8)式代入式(12),可得
(13)
对于一个非负整数N,可以得到
(14)
其中

(15)
(16)
(17)
把式(15)和式(17)代入式(11)中,用Vmθm代替v(t)。经过简化可以得到一阶惯性环节系统的带落角约束的最优制导律为
A2)Vmθm(t)+(A1f31+A2f32)am(t)-
A1zf-A2Vmθmf]
(18)
其中
A1=f31g22-f32g21
A2=f32g11-f31g12
(19)
如果导弹控制系统的响应时间较小或者飞行时间相对时间常数较大时,可忽略时间常数τ。在式 (18)中,令τ→0,zf=0,那么无惯性环节控制系统的带落角约束的最优制导律(Optimal Guidance Law with Impact Angle Constraint, OGL/IAC-0)为
(20)
其中
(21)
上述制导律需要已知z(t)和θm(t)的值。可以通过测量导弹和目标的视线角信息θ(t)来计算z(t)的值。此时,θ(t)可以近似为
(22)
那么式(20)可以改写为
(23)
实际中,对于N>0的情况,制导增益是可行的,因为当接近目标时制导指令是趋近于0的。这个特性很重要,因为它能保证抵抗外界干扰的不确定性、模型的不确定性和制导命令饱和限制。如果导弹的速度由于空气阻力而减少,那么可以通过选择一个较大的制导增益来避免性能的恶化。相反地,一个小的增益可以降低感应噪声的灵敏度。对于大多数的情况,理想的制导增益都是通过非线性仿真来选择。
2 剩余时间估计方法
针对上述制导律,最常用的也是最简单的剩余时间估计方法是用剩余距离除以导弹速度,即tgo=R/Vm。这种方法在弹道弯曲时会产生较大误差。为此,本文考虑将OGL/IAC-0的轨迹通过剩余路程的N阶多项式函数来近似。
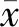


(24)

(25)
为了求解式(24)和式(25)中的系数,需要N+4个边界条件。当N=0时,由文献[5]可知,存在4个边界条件,包括t和tf时刻的位置和飞行路径角
(26)
当N>1时,需要N个额外条件,可以给定t=tf时刻的加速度条件为
(27)
由于Vm为常值,tgo可以通过路径的长度除以导弹的速度得到

(28)
式(28)表示的剩余时间可以理解为距离除以速度再乘以由于路径的弯曲而导致长度增加的一个补偿项。在以下给定的近似条件下
(29)
对于每个N值可得到k的值为
(30)

3 仿真结果
仿真条件如下:导弹初始位置为(0,2000)m,目标位置为(1200,0)m,导弹速度为VM=200m/s,初始弹道倾角θM(0)=0°,期望的落角θf分别取30°,60°,90°。

表1所示为采用传统方法和本文方法对导弹剩余时间进行估计的相对误差。由表1中可知,相对于传统的剩余时间计算方法tgo=R/Vm,本文提出的剩余时间估计方法对所有的N都有很高的精度。

(a)弹道轨迹

(b)剩余时间估计图2 θm0=60°,θmf=-60°时仿真结果Fig.2 Simulation results under θm0=60°,θmf=-60°

(a)弹道轨迹

表1 导弹剩余时间估计相对误差Δtfmax/tf(%)Tab.1 Fractional error of time-to-go estimation
4 结论
本文采用最优控制理论设计了考虑落角约束的闭环制导律,针对所需的剩余时间估计问题,基于导弹飞行近似轨迹,提出了一种实用的剩余时间估计算法。仿真结果表明,该方法相对于传统的估计方法,在不同的落角约束和制导增益条件下,相对精度平均提高了13倍以上。
