部分斜拉桥斜拉索锚固和传力安全性分析

2020-07-28张淼钱永久徐佰顺

哈尔滨工程大学学报 2020年3期

张淼，钱永久，徐佰顺

(1.西南交通大学土木工程学院，四川成都 610031； 2.内蒙古大学交通学院，内蒙古呼和浩特 010070)

部分斜拉桥的桥塔较矮，亦称矮塔斜拉桥。1994年由日本首次建造的小田原港桥[1]，具有连续梁桥和斜拉桥的特点。这种桥型造型美观、跨越能力大、施工方便且造价低廉，近年来日益兴起并广泛应用[2-3]。设计者们对部分斜拉桥的设计理论的研究也不断深入。卫康华等[4]对一三塔四跨矮塔斜拉桥成桥状态下各设计参数进行了敏感性分析。徐佰顺等[5]分析了大跨径曲线部分斜拉桥主梁的应力和挠度随设计参数的变化规律。许智强等[6]采用Monte-Carlo法建立随机车辆荷载模型，并利用有限元方法研究了斜拉桥索梁锚固区的疲劳特性。随着部分斜拉桥跨度的不断增大，混凝土箱梁结构不断向宽箱和大悬臂方向发展，这也对箱梁的设计提出了更高的要求。朱佩章等[7]研究了箱梁畸变、剪力滞和扭转等空间效应对部分斜拉桥主梁应力分布的影响。周效国等[8]对矮塔斜拉桥双边箱形主梁索梁锚固区进行了应力分布特点研究。崔春义等[9-10]利用ADINA对长山跨海矮塔斜拉桥地震动力响应特性和全桥受力状态进行了三维数值分析。罗强等[11]研究了矮塔斜拉桥索力在主梁锚固区的传递角度以及后浇带对主梁剪力滞效应的影响。

对于斜拉索锚固在箱梁大悬臂端部的部分斜拉桥，在斜拉索索力作用下，主梁悬臂端将产生较大内力[12]，同时在三向预应力作用下梁体结构内力分布更加复杂，这对梁体安全性能提出了要求。鉴于此，通过建立某矮塔斜拉桥宽箱长悬臂梁的空间有限元模型，研究斜拉索锚固区应力分布、竖向剪力分配情况及悬臂段安全性能，以期对矮塔斜拉桥的设计和施工起到指导性作用。

1 某三跨预应力混凝土部分斜拉桥工程概况

某三跨预应力混凝土部分斜拉桥，其跨径组合为108 m+208 m+108 m，平面位于曲线半径为1 800 m的圆曲线上。采用三跨连续刚构、塔墩梁固结体系，边墩处设置支座。桥塔采用三立柱型塔，桥面以上塔高28 m，主墩采用三柱式桥墩，承台横桥向分离。主梁采用C60三向预应力混凝土箱形梁；主梁截面采用变高度单箱双室直腹板箱梁，箱梁顶宽为20.5 m，翼缘板单侧悬臂宽度为4 m。在翼缘板端部设有小纵梁，小纵梁高1 m，宽0.4 m；箱梁中支点处梁高6 m，跨中及端支点处梁高3.8 m，梁高按二次抛物线变化。箱梁底板横向保持水平，桥面横坡由顶板斜置形成。箱梁横断面如图1所示。

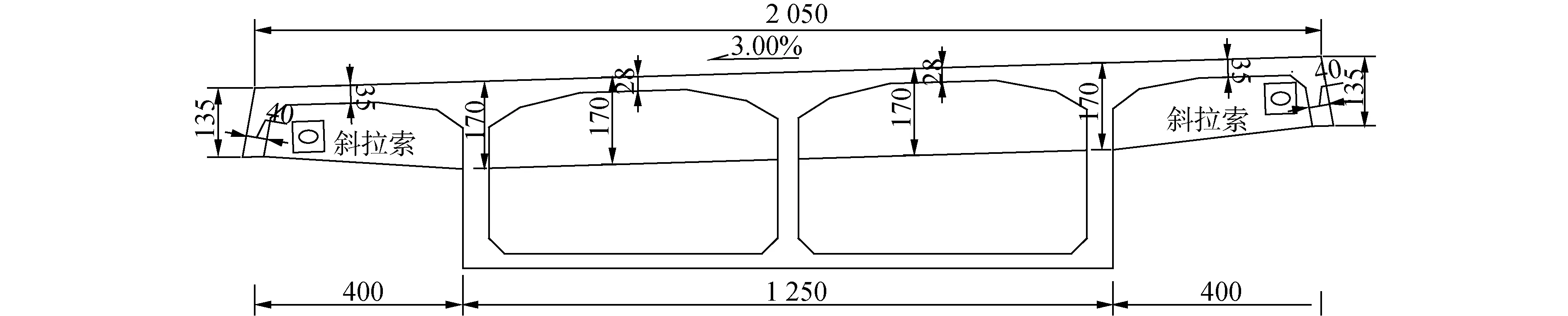
图1 箱梁横断面(单位：cm)Fig.1 Cross section of box girder

斜拉索锚固点处均设有横隔板，厚度为0.6 m，采用半横隔板形式。主梁共划分为28个节段，其中，0号节段长8.0 m，中合拢段及边合拢段长2.0 m，中节段长度分别取为3.0、3.5、4.0 m 3种。主梁无索区长度为索塔附近2×25 m=50 m，中跨跨中30 m，边跨19 m。斜拉索采用扇形布置，梁上间距8 m，塔上间距1 m。主梁分块及斜拉索布置如图2所示。

图2 主梁分块及斜拉索布置(单位：cm)Fig.2 Main beam block and arrangement of stay cables

2 某三跨预应力混凝土部分斜拉桥有限元模型

2.1 模型的建立

首先采用有限元分析软件MIDAS CIVIL建立整体杆系模型，提取最不利荷载工况下的截面内力。根据实际情况取首索附近梁段和尾索附近梁段进行分析，采用MIDAS FEA分别建立局部有限元模型。根据平截面假定和“圣维南”原理对模型进行简化，将模型一端截面的质心节点与其他节点刚性连接，并将整体杆系模型在最不利工况下的截面内力加载于质心节点，用来模拟结构其他部分对该部分模型的作用力。模型的另一端截面质心节点与其他节点也采用刚性连接，并将质心点与另一固结点间采用柔性连接，柔性连接为六自由度弹簧，刚度由整体模型计算。2类模型具体建模参数如下:

1)首索模型

首索模型计算位置取为主梁6～9号节段，模型共有161 417个节点，403 115个单元。模型考虑的预应力筋共131束，其中，横隔板预应力8束，顶板横向预应力19束，竖向预应力104束。首索模型柔性连接弹簧刚度如表1所示。

2)尾索模型

尾索模型计算位置取为主梁21～25号节段，模型共有99 330个节点，337 818个单元。模型考虑的预应力筋共140束，其中，横隔板预应力8束，顶板横向预应力20束，竖向预应力112束。尾索模型柔性连接弹簧刚度如表1所示。

表1 柔性连接弹簧刚度Table 1 Flexible connection spring stiffness MPa

3 主梁应力分析

3.1 最不利工况拟定

为保证结构正常使用阶段的安全性，对首索和尾索位置处的主梁应力进行验算。计算中考虑如下3种最不利工况：

1)工况1为首索索力最大工况，具体荷载组合为恒载+钢束一次+钢束二次+活载+整体降温+梯度降温+横风；

2)工况2为尾索索力最大工况，具体荷载组合为恒载+钢束一次+钢束二次+活载+整体降温+梯度降温+横风；

3)工况3为尾索处主梁底板最不利工况，具体荷载组合为恒载+钢束一次+钢束二次+活载+整体降温+梯度升温-顺风。

3.2 主梁应力计算结果

3.2.1 工况1

首索模型在工况1作用下，主梁应力分布情况如图3所示。当主拉应力大于1.96 MPa，主压应力大于0.6fck=-23.1 MPa时[13]，判定为主梁潜在危险区域，图3(c)为主梁主拉应力潜在区域所占的体积比例，由图可知主拉应力超限区域占模型体积的1.2%，其中最大主拉应力值为3.98 MPa，主要集中在斜拉索锚固区。由图3(d)可知，最大主压应力值为22.24 MPa,主压应力无超限区域。

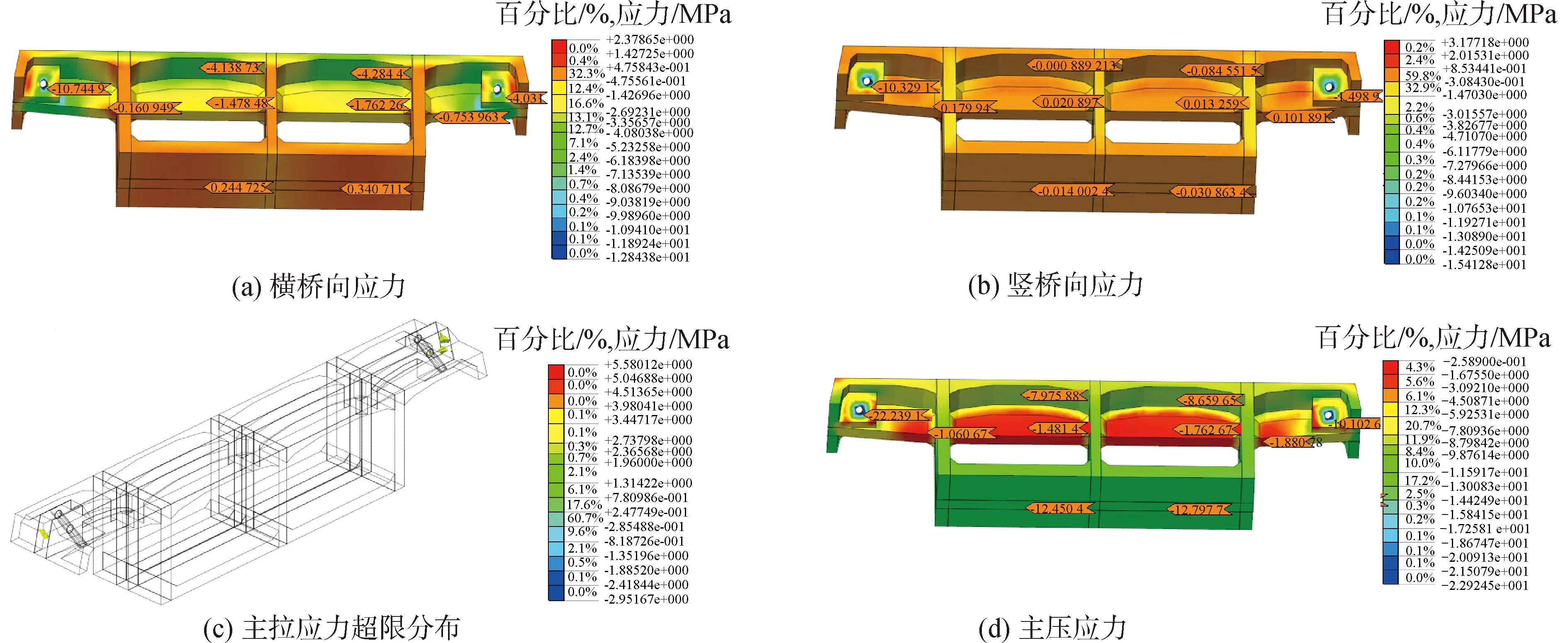
图3 工况1主梁应力分布Fig.3 Stress distribution of main beam under the first condition

3.2.2 工况2

尾索模型在尾索最大索力作用下主梁横桥向应力、竖桥向应力、主拉应力、主压应力的大小及分布情况如图4所示。图中还给出了主梁应力潜在危险区域所占的体积比例。由图4(c)可知，最大主拉应力为2.87 MPa，超过1.96 MPa部分体积占模型的0.5%，主要集中在锚固区域。由图4(d)可知，最大主压应力为20.1 MPa，没有超过23.1 MPa的区域。

图4 工况2主梁应力分布Fig.4 Stress distribution of main beam under the second condition

3.2.3 工况3

尾索模型在工况3情况下主梁横桥向应力、竖桥向应力、主拉应力、主压应力的大小及分布情况如图5所示。图中还给出了主梁应力潜在危险区域所占的体积比例。由图5(c)可知，最大主拉应力为3.58 MPa，超过1.96 MPa部分体积占模型的0.7%，主要集中在锚固区域。由图5(d)可知，最大主压应力为20.79 MPa，没有超过23.1 MPa的区域。

图5 工况3主梁应力分布Fig.5 Stress distribution of main beam under the third condition

将3种工况下主梁应力有限元分析结果进行整理，如表2所示。由表可知，横桥向和竖桥向最大拉应力值分别为2.23 MPa和3.35 MPa,主拉应力最大值为3.98 MPa，均出现在锚固区，超限区域所占比例均不超过1.2%。横桥向和竖桥向最大压应力值分别为11.90 MPa和13.10 MPa，最大主压应力为22.24 MPa，无超限区域。

表2 主梁应力计算结果Table 2 Main beam stress calculation results MPa

3.3 主梁(除去锚固区)应力计算结果

在斜拉索索力作用下，会导致主梁锚固区部分产生应力集中，通常梁体中的应力最大值产生于此处，考虑到在实际工程中，多采用一些构造措施减小锚固区应力，因此有必要对主梁去除锚固区部分进行应力分析，以便了解主梁应力分布及主应力超限情况。计算结果如表3所示。由表可知，在去除锚固区后主梁最大主拉应力为1.71 MPa，没有超过1.96 MPa的区域，最大主压应力为13.92 MPa，没有超过23.1 MPa的区域。

表3 主梁(除去锚固区)应力计算结果Table 3 Main beam(removal of anchorage zone)stress calculation results MPa

4 索梁锚固区剪力的分配

该桥斜拉索锚固在主梁两侧悬臂段的端部，且横隔板仅填充箱室上侧，在拉索作用下应力分布十分复杂。在主梁悬臂段4 m范围内，竖向剪力主要由翼缘板和横隔板共同承担，但相互之间分配关系尚不清楚。同类桥梁在设计时偏于保守的取剪力全部由横隔板承担，从而横隔板需要配置一定数量的抗剪钢筋且偏厚重才能满足设计要求。实际上翼缘板也承担一部分剪力，因此，有必要考察横隔板所承担剪力的比例，从而指导横隔板设计。

4.1 荷载标准组合下锚固区剪力分配

研究索力作用下梁索锚固区的剪力分配问题，首先对整体模型通过影响线加载的方法求出索力最大值，再将索力最大值与其他荷载进行标准组合，即可求出施加在模型上的荷载值。首索模型和尾索模型分别考虑首、尾索索力最大为计算条件，分析时选取截面1、截面2、截面3分别为距主梁中心线距离为7、7.5、8.5 m的3个截面，以此研究横隔板在不同区域分配的剪力。

计算结果如表4所示。由表可知，首索位置处的竖向剪力由横隔板承担约40%，翼缘板承担约60%，且横隔板承担的竖向剪力大小与截面位置相关，截面1、截面2和截面3承担的竖向剪力比例分别为37%、42%和44%，可见横梁越靠近锚固端承担的剪力越大。

表4 横隔板各截面剪力Table 4 Shear force of each section of the diaphragms

4.2 特殊荷载下锚固区剪力分配

为进一步讨论锚固区剪力分配问题，讨论几种特殊荷载作用下锚固区剪力分配状况。由于首索处斜拉索与桥轴线夹角最大，竖向剪力最大，因此选取首索模型为研究对象。拟定2种计算条件：

1)仅索力荷载，即全桥仅考虑索力，去除包括结构自重、活载、温度荷载等在内的所有其他荷载，并且重新定义边界条件；

2)单根索力荷载，即仅考虑首索索力，去除所有其他荷载，并且重新定义边界条件。

取索梁锚固区域隔离体作为分析对象，如图15所示。对隔离体竖向剪力进行分析，索力的竖向分力引起的竖向剪力由3个面承担，分别命名为翼缘板端面1、翼缘板端面2以及侧面，其中侧面可分为横隔板，翼缘板侧面1和翼缘板侧面2。

图15 锚固区域隔离体(单位：cm)Fig.15 Anchorage isolation

将计算结果进行整理，如表5所示，表中给出了各面分配剪力值及其所占比例。计算结果表明，在仅索力荷载作用下，剪力由各面承担，翼缘板端面承担21.2%，翼缘板侧面承担38.0%，横隔板承担40.8%。在仅首索索力荷载作用下，剪力由各面承担，翼缘板端面承担29.8%，翼缘板侧面承担30.6%，横隔板承担39.6%。

表5 锚固区隔离体剪力分配情况Table 5 Shear force distribution of anchorage isolation

通过对斜拉索锚固区剪力的传力分配情况研究表明：梁索锚固区竖向剪力由横隔板和翼缘板共同承担，在荷载标准组合作用下：首索位置和尾索位置横隔板承担剪力比例分别分44%和45%；在考虑特殊荷载时，仅索力和仅首索索力作用下，首索位置横隔板承担剪力比例分别为40.8%和40.1%，可见，横隔板承担剪力比例不超过50%,设计中可按横隔板和翼缘板共同抗剪进行设计。