基于改进CUOWGA算子-Sharpley值的应答器传输系统风险评价方法

2020-07-28褚心童张亚东

铁道标准设计 2020年8期

褚心童,张亚东,李耀

(西南交通大学信息科学与技术学院,成都 611756)

随着我国高速铁路的飞速发展，高速铁路安全运营越来越受到人们关注。应答器传输系统作为列车运行控制系统中重要的地-车信息传输子系统，在保证列车安全高效运行方面起到了极其重要的作用[1]。如何更加科学、合理地对应答器传输系统进行风险评价，对保障高速铁路安全运行具有重要意义。

危险与可操作性分析 (Hazard and Operability Analysis，HAZOP) 方法是一种系统化的辨识方法，结构化程度较高。HAZOP将系统划分为若干功能相对独立的节点，并提取分析要素，通过设计引导词，辨识系统中潜在的危险及影响。目前广泛运用于系统安全风险分析领域[2]。

由于HAZOP方法属于定性分析，无法对识别出的风险进行量化评价。因此近年来国内外学者在HAZOP方法基础上，综合ANP分析[3]、模糊综合评价法[4]、偏移度量化分析[5]等方法，对定量风险评价进行了研究。但这些方法未考虑风险事件间的相关性，并且如何进一步降低风险评价中专家决策的主观性需要深入研究。

CUOWGA算子是一种改进的OWGA(有序加权几何平均)算子[6]，它可以对不确定环境中的一组区间数据，基于数据间两两比较的可能度公式及模糊互补判断矩阵公式进行集结决策，降低决策者带来的主观影响，得到可信度最高的数据区间。CUOWGA算子目前已经在多属性决策[7]、聚类分析[8]等领域得到广泛应用。

而Sharpley值是一种基于合作博弈论的利益分配方式[9]，它可以计算各成员在考虑相互联盟的情况下对于整体的相对重要程度或权重[10]。根据这一特点，可以计算安全性分析领域中多风险相关下的评价因素权重值。

本文方法首先对被测系统建立功能分层模型，使用HAZOP方法辨识模型潜在的风险及影响；根据辨识结果建立评价因素集，结合模糊统计法建立评判集；邀请5人专家组使用评判集对各底层因素进行模糊评价并量化为置信区间；使用改进的CUOWGA算子集结各专家评价，降低专家评价主观性，获得各单一因素的风险评估值；利用Sharpley值函数，计算在考虑风险相关性的情况下，各下层评价因素对上层评价因素的影响权重；根据各下层因素的风险评估值及权重，使用加权平均法计算上层评价指标的风险评估值；重复上述步骤，最终获得被测系统的整体风险等级。本方法利用模糊统计法、CUOWGA算子及Sharpley值相结合，全面整合了专家组评价，降低了专家主观影响及经验差异，且考虑了多风险相关性，对应答器传输系统的风险评价提供了新方法。

1 系统建模与HAZOP分析

1.1 功能分层模型

本文利用功能分层模型对系统功能进行建模描述。功能分层模型能够描述系统的功能分层结构，根据功能涵盖的范围，以树状图的形式自上而下进行功能分解[11]。某典型功能分层模型如图1所示。

图1 典型功能分层模型示意

功能分层模型能帮助研究人员根据底层功能风险程度，自下而上地完成整个系统的风险评估。

1.2 HAZOP风险识别

基于功能分层模型，运用HAZOP方法对模型中的潜在的风险事件及其影响进行识别，建立HAZOP分析表[12]，包括以下内容。

(1)节点：系统具体的设备单元、功能、操作过程及状态。

(2)要素：同一节点中可能具有的不同特征，是节点的细化。

(3)引导词：用于描述对要素设计意图偏离的词或短语。常用引导词及含义见表1[13]。

表1 常用引导词含义

(4)偏差：一般为“要素”与“引导词”组成的短语，即识别出的故障模式。

(5)发生原因：从设备单元的硬件、软件、外界条件等方面分析产生风险或故障的原因。

(6)可能后果：风险可能导致的后果或影响。

按照功能分层模型的层次划分，结合“节点”及“要素”的定义，将功能分层模型中的中间功能{FⅠ，FⅡ}作为HAZOP分析节点，底层功能{{F1，F2}，{F3，F4}}作为分析要素展开分析。

2 系统风险评价方法

2.1 构建评价因素集

评价因素集是指决策系统中影响评判的各种因素所组成的集合[14]。本方法中可将HAZOP辨识出的所有偏差{u1，u2，…，um}作为评价因素集U。以图1展示的典型功能分层模型为例，结合各偏差所属的节点{uⅠ，uⅡ}，可将评价因素集U表示为

U={uⅠ，uⅡ}={{u1，u2}，{u3，u4}}

其中，uⅠ表示节点FⅠ的所有偏差组成的评价因素子集，u1表示要素F1辨识出的偏差的评价因素。

2.2 构建标准评判集及模糊评判集

评判集是指对评估标准进行划分而得到的各风险等级的集合。根据EN50126标准中对列控系统风险级别的说明，将其作为标准评判集G={G1，G2，G3，G4}={“可接受的”，“可容许的”，“不期望的”，“不可接受的”}[15]。

传统方法中，往往将评判集量化为确定数值，主观性较强。为解决这一问题，将评判集量化为区间数。定义风险等级最大值为1，最小值为0。根据等分原则，标准评判集可表示为G={G1，G2，G3，G4}={[0，0.25]，[0.25，0.5]，[0.5，0.75]，[0.75，1]}。

当专家进行风险评价时，受限于经验认知或现场环境复杂等条件，标准评判集的4等级划分较为模糊。为便于专家给出客观评价，将风险等级扩展为7级，定义模糊评判集V={v1，v2，…，v7}={“最小”，“很小”，“较小”，“一般”，“较大”，“很大”，“最大”}。其含义及对应量化区间如表2所示。

表2 模糊评判集量化含义

2.3 单因素评判集

2.4 基于CUOWGA算子的专家评价集结

CUOWGA算子是一种针对区间决策数据的集结方法，有利于解决模糊性问题。集结过程中引入规范化决策矩阵及可能度矩阵，降低了专家个人主观性及专家间经验差异性带来的影响[16]。

传统CUOWGA算子获得的结果与评判集量纲不同，本文针对此增加了算子-评判集转换步骤。以n个专家参评包含m个风险事件的因素集为例，具体计算过程如下。

(1)专家位置权重ω=(ω1，ω2，…，ωk，…，ωn)

(1)

其中，Q(r)为模糊语义量化算子

(2)

其中，a，b，r∈[0，1]。规定模糊语义计算原则分别为“至少半数”“大多数”“尽可能多”的前提下，Q(r)中的参数[a，b]对应取值为 (0，0.5),(0.3，0.8),(0.5，1)。

(3)

令la=aU-aL，lb=bU-bL，定义：

(4)

(5)

(5)规范化评判数据排序

(6)计算CUOWGA算子

利用位置权重ω，对b(k)进行加权处理，得到因素uk的CUOWGA算子

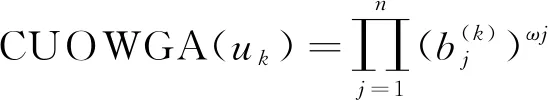
(6)

因素集的CUOWGA算子可表示为CUOWGA(u1，u2，…，um)。

(7)算子-评判集置信区间转换

利用式(3)的逆推公式，获得因素uk的集结评判数据J(uk)，其中

(7)

因素集的集结评判数据可表示为J(u1，u2，…，um)。

2.5 基于Sharpley值函数的因素权值计算

由于在应答器传输系统中，各风险可能同时出现且相互影响，风险相关性的评估对评价结果的准确性至关重要。Sharpley值函数本质是一种考虑成员可以联盟的情况下，按各成员对整体贡献度进行分配的一种分配方式[17]。将其引入安全性分析领域，可以合理分析在考虑风险相关性的情况下，各因素对因素集的影响权重。具体步骤如下[18]。

(1) 集结评判数据归一化

对集结评判数据J(u1，u2，…，uk，…，um)进行归一化处理，得到归一化评判数据C(c1，c2，…，ck，…，cm)。

(8)

(2)计算因素组合影响程度

将因素集中所有可能同时出现的因素组合用集合S表示，s表示其中的一种组合方式。组合s对因素集的影响程度v(s)可表示为

(9)

其中，σ表示关系系数，uk表示组合s包含的一个因素，ck表示uk的归一化评判数据。v(s)计算值大于1时取值为1。

组合方式s中包含的因素相互影响时，关系系数σ取1.2，增强影响程度；当各因素相互独立或s包含所有因素时，关系系数σ取1。

(3)计算各因素的风险相关权重

根据Sharpley值的计算公式，因素uk对因素集的影响权重φk可表示为

(10)

其中，|s|表示组合方式s中含有的因素个数；v(s)表示组合s对因素集的影响程度；v(s/k)表示组合s剔除因素uk后形成的新组合对因素集的影响程度；n是因素集包含的因素个数，w(|s|)表示组合s的加权因子。

2.6 加权综合评判

根据各因素的集结评判数据J(u1，u2，…，um)及权重(φ1，φ2，…，φm)，运用加权平均法计算因素集U的综合评判值Z(U)，可表示为

(11)

3 案例分析

应答器传输系统是列控系统的重要地-车信息传输子系统，也是保障列车安全运行的关键设备[19]。论文以应答器传输系统为对象进行方法应用与验证。

3.1 构建评价因素集

应答器设备由地面、车载两部分设备构成。车载设备包括BTM与天线单元，地面设备包括LEU及地面应答器。应答器设备结构如图2所示[20]。

图2 应答器设备结构

应答器系统的核心功能，是实现地面设备与车载设备之间信息的安全传输，而系统核心功能的实现，需要地面应答器功能、LEU功能、BTM及天线单元功能的共同支撑[21-22]。

根据应答器系统结构，建立三层功能分层模型。最上层为应答器传输系统功能；第二层为应答器部件功能；第三层功能为各部件具体功能，也是最简洁、不能继续分解和细化的功能。。

利用HAZOP对功能分层模型进行风险辨识，可得到如表3所示的应答器系统功能分层模型风险识别表。共识别出风险偏差11个，由于篇幅限制，仅列出部分辨识结果。

表3 应答器传输系统功能分层模型风险辨识

根据HAZOP辨识结果，将11个风险偏差编号，并建立应答器风险评价因素集U={uⅠ，uⅡ，uⅢ}={{u1，u2，u3，u4}，{u5，u6，u7}，{u8，u9，u10，u11}}，如图3所示。

图3 应答器风险评价因素集

3.2 单因素评判

邀请5人专家组对因素集的底层因素进行单因素评判。以“地面应答器功能失效”因素子集uⅠ为例，共包含4个因素。评判数据如表4所示。

表4 专家组模糊评价数据

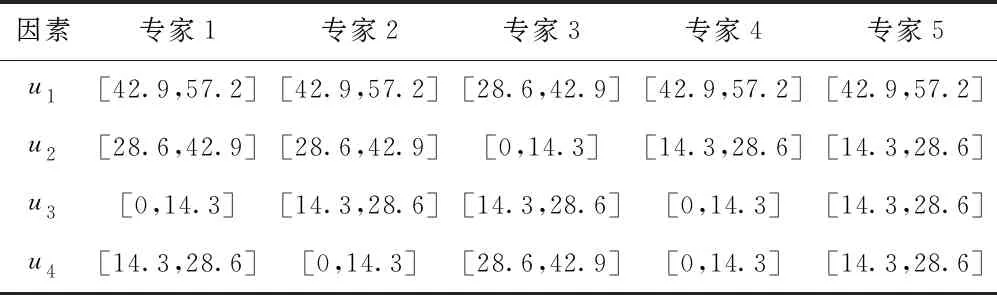
表5 单因素评价矩阵

3.3 专家评价集结

(1)计算专家位置权重

对风险预测时，应考虑风险最大的情况，因此选择模糊语义为“尽可能多”，即[a，b]取值为(0.5，1)。根据式(1)、式(2)计算可得，专家位置权重为

ω=(0.4，0.4，0.2，0，0)

(2)单因素评判矩阵规范化

表6 规范化评判矩阵

同理，可得其余3个因素的可能度矩阵如下

b(1)=

b(3)=

(7)计算CUOWGA(u1，u2，…，u4)

根据式(6)，结合位置权重ω，可计算各因素的CUOWGA算子

CUOWGA(u1，…，u4)=

(8)根据式(7)计算集结评判数据

J(u1，…，u4)=

([42.9，57.2]，[0，23.5]，[0，24.9]，[0，29.3])

3.4 因素权值计算

根据上述集结评判数据的中间值，计算多风险相关下的底层因素对因素子集uⅠ的影响权重。

(1)根据式(8)，对集结评判数据中间值进行归一化处理

C=[0.563 0，0.132 2，0.14，0.164 7]

(2)将因素{u1，u2，u3，u4}随机组合，根据式(9)各组合对因素子集uⅠ的影响程度v(s)如表7所示。

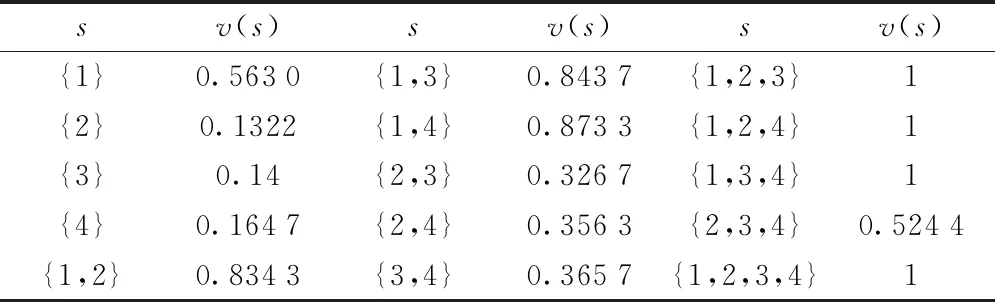
表7 各组合影响程度数据

(3)根据表7及式(10)，计算各因素权值

φ1(v)=0.598 5；φ2(v)=0.124 0

φ3(v)=0.129 7；φ4(v)=0.145 8

3.5 加权综合评判

(1) 因素子集综合评判

将各底层因素的集结评判数据J(u1，u2，…，um)及权重(φ1，φ2，φ3，φ4)，应用式(11)计算得因素子集uⅠ“地面应答器功能失效”的综合评判值Z(uⅠ)=[25.7，44.6]。

选取不同因素子集，重复3.3节内容，可计算得：“LEU功能失效”Z(uⅡ)=[15.1，28.9]，“BTM及天线功能失效”Z(uⅢ)=[41.3，54.6]。

(2)因素集U综合评判

将因素集U={uⅠ，uⅡ，uⅢ}作为评价集合，{Z(uⅠ)，Z(uⅡ)，Z(uⅢ)}作为{uⅠ，uⅡ，uⅢ}的集结决策数据，重复3.4节内容计算权值，再利用式(10)获得因素集U“应答器系统失效”综合评判值Z(U)为[30.9，46.1]。

取Z(U)中值38.5作为“应答器系统失效”的最终评价值，则根据标准评判集可知，应答器系统功能失效等级为“可容许的”，该结果与现场使用情况相符，表明基于改进CUOWGA算子-Sharpley值的应答器传输系统风险评价方法是有效的。同时，根据因素子集的综合评判值大小，可发现“BTM及天线单元功能失效”对系统整体影响最大，应采取措施重点防护。