铁路信号联锁表计算机辅助设计主要算法与量化策略研究
2020-07-28李茂蛟
李茂蛟
(中铁工程设计咨询集团有限公司,北京 100055)
1 概述
联锁表是车站信号设备联锁关系的信息说明图表,以进路为单元,表达了进路与进路、进路与道岔及进路与信号机之间的制约关系。
铁路信号设计人员完整地编制联锁表不仅是一项重要而繁琐的设计工作,而且编制过程中很容易出现差漏,尤其是敌对信号及其敌对条件的差漏。利用计算机辅助设计是大幅提高联锁表编制效率的唯一途径。但相关技术标准[1-3]及文献[4]中仅从宏观层面对联锁表编制的格式、内容以及敌对进路等概念进行了规定与定义,而基本进路与变更进路的选择、变更按钮的选择等内容均具有较强的主观性,以上因素都不利于计算机的自动处理。
本文对信号设备平面布置图的结构化表达、联锁表进路的主要处理算法进行研究,以实现联锁表的计算机辅助设计。
2 信号设备平面布置信息化表达
结合图论中“图”的概念[5],将信号设备平面布置图中信号机、绝缘节、道岔、轨道区段等抽象为含属性的基本节点单元,则可将信号设备平面布置图视为一张从左至右或从右至左的有向图[6]。
为便于处理,对上述节点单元采用统一数据结构进行描述,具体的节点单元数据结构包括设备类型代码、设备名称及相关属性等字段。
为精简接口数据,结合联锁“进路”与图论“路径”的概念,按从左至右的顺序将一条进路中的所有节点单元按序组成一束路径数据,则全站信号设备平面布置图的拓扑结构可由若干束路径数据进行描述。
本文以符号v(x)表示设备x节点信息,以节点集合Rd={v(x1),v(x2),…,v(xn)}表示一条进路和路径中顺次经过的所有节点,其中,xi为进路或路径中第i个设备名称,n表示节点数量。在不涉及具体设备名称的情况下,将v(xi)简写为vi。


图1 示例车站信号设备平面布置示意

全站的进路搜索空间可表示为
Rd=[Rd1,Rd2,…,Rdn]T
(1)
其中,
Rdi={vi,1,vi,2,…,vi,m}
(2)
其中,m表示第i条路径Rdi上所有的节点数量。
由此,可根据节点邻接关系及具体属性,采用图论中相关路径搜索算法进行进路搜索。对于图1所示车站,全站若分咽喉表示,仅需8束路径数据即可实现联锁表设计所需的全部信息的结构化存储。
实现车站信号设备平面布置的结构化表达,可有以下两种方式。
(1)人工编制结构化接口数据
设计人员根据车站实际的信号设备平面布置示意图,按照上述路径数据单元的表达方式,对车站的所有路径逐条编制相应的路径数据。该方法对平面图绘制无特殊需求,且适合对既有纸质版平面布置图进行结构化表达。
(2)计算机辅助设计
需在计算机辅助设计信号平面布置图时,根据需要将相关信息附加到相应的设备图元上,这样,平面图本身就包含了所需的信息,通过计算机程序根据需求即可提取所需的设备属性及设备连接关系等信息。该方法一方面需要信号平面布置图的绘制(本文仅讨论AutoCAD制图形式)遵循严格的规定,如需采用预先定义的图块单元来表达信号机、联锁道岔等信号设备,还需要为这些图块单元分别附加相应的属性;另一方面,需要编制相应的AutoCAD插件,以提取相关属性,从而根据上述路径数据定义生成全站的路径数据。
3 进路搜索算法与变更进路量化选择策略
图论中,路径搜索算法有深度优先(DFS)[7]、广度优先(BFS)[8]等多种搜索算法,对于本文采用的进路数据束结构,仅在道岔节点处有分支存在,本文采用DFS算法作为进路搜索核心算法,内存消耗较BFS算法小,且可在搜索过程中对搜索方向进行优化限制,如可限制直股优先或弯股优先。
3.1 进路基础搜索算法
以Rt表示进路空间,以点v1表示进路搜索起始节点,以式(3) 表示搜索到节点vi时,已顺序访问的节点集合。
V(vi)={v1,v2,…,vi}
(3)
对于某节点vi(i>1),其父节点为vi-1,其子节点集合可表示为Vs(vi)={vi,j,j=0,1,2,…,k},其中,k表示子节点数量(k=0表示无子节点,即vi,0=∅)。
不失一般性,以vc表示(任意)当前节点,则DFS(vc)递归过程如下。
a)令R=V(vc),判定是否构成合法的进路,若是,则将R存入Rt,并转d),否则转b);
b)搜索得vc子节点集合Vs(vc),若Vs(vc)=∅,则转d),否则转c);
c)对Vs(vc)中每个有效节点vc,j,分别递归调用DFS(vcj);
d)令R=V(vc-1),返回上层递归状态,若无上层递归,则结束;
由上述DFS算法过程可知,要实现进路搜索,需要设计合法进路的判定函数F(R),例如,对于式(3)中节点列表R=V(vi),若始端v1为出站信号机,终端vi为进站信号机,且二者方向相反,则可判定为合法的列车发车进路。
联锁系统中,进路需有明确的始端和终端,因此,进路搜索首先需提取进路始端设备,然后根据始端设备属性,搜索所有可能的进路。对每一个进路始端节点,采用DFS算法,搜索以该节点为始端的所有合法进路,并将每条搜索出的进路存放于进路空间,最终得到全站所有的进路集合。
Rt=[R1,R2,…,Rn]T
(4)
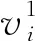
(5)
对于某进路R,根据式(5)所示的节点集合,可相应提取道岔、轨道区段等信息。以W(R)表示进路R内道岔及防护道岔(含道岔状态)的集合,以T(R)表示进路R内的轨道区段集合。
3.2 基本进路量化选择策略
在工程实际应用过程中,工程人员提出了不少基于经验的确定基本进路与变更进路的规则与见解[9-10],但通常依赖于联锁表编制人员对于平面图的直观观察与理解,其基本进路与变更进路的比选没有量化指标,不便于计算机处理。
从进路之间相互关系出发,提出一种量化的进路比较算法,为每条进路赋予相应权值,从而根据权值大小确定基本进路与变更进路。
根据两条进路所经过道岔的状态与轨道区段的相互关系,将两条进路Ra与Rb之间关系定义为以下三类。
(1)相互独立。若W(Ra)与W(Rb)无相同道岔(同一道岔的定位与反位状态视为相同道岔),且T(Ra)与T(Rb)无相同轨道区段,则Ra与Rb相互独立。
(2)相互排斥。若W(Ra)与W(Rb)分别包含至少1组相同道岔的两种状态(定位/反位),则Ra与Rb相互排斥。
(3)相互重叠。若W(Ra)与W(Rb)不包含同一道岔的不同状态(定位/反位),且T(Rb)包含至少1个相同轨道区段,则Ra与Rb相互重叠。
在不作特殊限制的情况下,相互独立的进路能够同时开放,列车经独立进路相互之间不冲突;相互排斥的进路因道岔状态冲突,是不可能同时开放的;相互重叠的进路能够同时开放,但列车经相互重叠的进路可能发生冲撞。
对于进路空间Rt中的任意进路R,与之相互独立的的进路数量Nd(R)越大,则说明受其影响的进路越少,因此,采用Nd(R)作为衡量进路影响的权值。
对于始端vs与终端ve均相同的m条进路构成的进路空间如式(6)所示
R(vs,ve)=[R1,R2,…,Rm]T
(6)
对式(6)所示进路空间按进路权值由大到小进行排序,得到
Rs(vs,ve)=[Rs,1,Rs,2,…,Rs,m]T
(7)
则标记Rs,1为基本进路,其余为变更进路。
如图2所示为京张高铁某车站右咽喉的信号设备平面布置示意,以SN至IG接车进路为例,存在两条进路R1、R2,其顺次经过的道岔状态分别如式(8)、式(9)所示
W(R1)={2,8,16,20}
(8)

(9)
依据上述量化策略,计算两条进路的权值分别为Nd(R1)=25,Nd(R2)=13,判定R1为基本进路,R2为变更进路。
由图2可知,当R2进路排出时,由S、SC接车至IIG、4G、6G及由IIG、4G、6G向S、SC口发车的共12条进路无法排出,而当R1进路排出时,上述12条进路不受影响,上述12条进路即Nd(R1)与Nd(R2)的差值所在。另一方面,R1为直向进路,R2为八字进路,以上量化策略判定R1为基本进路,也与实际经验相符。

图2 某站右咽喉信号设备平面布置示意
3.3 不合理进路判定策略
对始端vs与终端ve相同的两条进路Ra与Rb,不失一般性地,假设Ra为基本进路,Rb为变更进路。若T(Rb)⊇T(Ra),即基本进路内的轨道区段均包含于变更进路内的轨道区段,则标记Rb进路不合理。一般来说,对于上述情形,如果变更进路Rb能办理成功,则基本进路Ra亦能办理成功,就没必要办理影响范围大的变更进路。当然,实际应用时可仅对判定的不合理进路进行存疑标记,由设计人员参考相关部门意见后确定是否删除以上不合理进路。
对于式(7)所示的进路集合,对于m>2(即具有两条及以上的变更进路)的情况,需要依次对所有变更进路进行标记。即对于式(7)中已排序完毕的变更进路Rs,i(i>1),对任意j T(Rs,i)⊇T(Rs,j) (10) 若两条(或两条以上的)进路能同时办理(即进路不相互排斥),但同时办理以后有可能造成冲突的进路称为敌对进路[11-12]。根据文献[2]对敌对进路的划分,将敌对进路归纳为以下两种类型。 (1)重叠型敌对进路。根据本文对相互重叠进路的定义可知,与进路R相互重叠的进路可判定为进路R的敌对进路。 (2)侵限型敌对进路。防护进路的信号机设置在侵限轨道绝缘节处,不准许同时开通的进路。关于该进路,以图3为例,对于D8至ⅡG的调车进路R(D8,XⅡ),由于D14处绝缘节侵限,为避免侧面侵限冲突,禁止办理以D14为终端的调车进路,该类进路为敌对进路。 图3 某站信号平面布置图局部示意 对于式(4)所示的进路空间Rt中的进路R,若存在某进路Rj≠R,使得Rj与相互重叠,则判定Rj为R敌对进路,并将添加至R的敌对进路空间Rc(R)中;否则继续判定是否为R的侵限型敌对信号,判定流程如下: a)从T(R)提取绝缘节处为侵限的信号机集合S; b)若S为空,则返回,否则转c); c)对S中的每一个信号机vs,从进路空间中搜索以vs为终端,且与相互独立的进路子空间Rs,若Rs≠∅,则Rs中各进路均为的敌对进路,将Rs添加至R的敌对进路空间Rc(R)中。 至此,即完成了R的敌对进路搜索,得到其敌对进路空间表示如式(11) Rc(R)=[R1,R2,…,Rk] (11) 对于进路Ra,其敌对进路的始端信号即为其敌对信号,其敌对类型与敌对进路类型一致。例如,若Rb为Ra的列车敌对进路,则Rb始端信号为Ra的敌对列车信号。 对式(11)所示的R的敌对进路空间,按照进路类型,提取其始端信号,构成无重复的始端信号集合如式(12) (12) c)初始化道岔集合Win=∅和Wout=∅,分别表示进路内和进路外道岔条件; d)对于每条进路Rx∈Rt(sj)且Rx∈Rc(R),取其道岔集合W(Rx)中第一个包含于W(R)中的道岔状态wx,in,若wx,in∉Win,则将wx,in添加至Win; e)对于每条进路Rx∈Rt(sj)且Rx∈Rc(R),取W(Rx)中最后一个不包含在W(R)中的道岔状态wx,out,若wx,out∉Wout,则将wx,out添加至Wout; 最终,若Win不为空,则Win中的道岔状态即为进路内敌对条件;Wout不应为空(否则应为无条件敌对),Wout中的道岔即为进路外敌对条件,二者选其一作为敌对条件即可。 图4 某车站过渡阶段平面布置局部示意 本文主要讨论关键道岔提取算法和变更按钮选择算法。前者具有确定性,不受编制人员主观影响,但其判定逻辑和算法实现并不直观,值得讨论;后者往往具有较大的主观性,在计算机处理时,需确定其量化比较策略。 文献[13]规定,当有两种以上运行方式时,为区别开通的进路,需填写关键对向道岔的位置(定位/反位)。将从算法层面探讨关键道岔的搜索方法。 对于任意两条始端vs与终端ve相同的进路,二者由始端开始,必然分别经由某个道岔wf的不同位置产生分支,方能形成不同进路;之后必然再分别经由某个道岔wh的不同位置重新汇聚,方能到达同一终端。这里,产生分支的道岔wf,以下称为二分道岔,其定位与反位即为两条进路的关键道岔位置。例如,假设基本进路R0(vs,ve)和变更进路的道岔状态集分别如式(13)和式(14)所示 W0={wf,w0,1,w0,2,…,wh,…,w0,k} (13) (14) 则显见,两条进路分别经由道岔wf的定位和反位产生分支,经由道岔wh的定位和反位最终汇聚。因此,道岔wf的定位与反位即为两条进路的关键道岔位置。 在排列变更进路时,为区分于基本进路及其他变更进路,需在始端按钮、终端按钮之间设置变更按钮[14]。对于进路R,以Sg(R)表示进路内始端按钮和终端按钮之间的可用作变更按钮的调车信号集。 若变更进路Rb对应的Sg(Rb)中有可用作变更按钮的调车信号,则可选择合适的调车信号按钮作为变更按钮;否则,需在进路中合适的区段单独设置变更按钮。本文对以下问题的量化解决方案进行讨论。 (1)进路中有多个调车信号可设为变更按钮时,如何选择。 (2)需单独设置变更按钮时,设置于进路中哪个区段。 变更按钮的作用在于与始端按钮、终端按钮按照顺序唯一确定一条进路,因此,在保证始端按钮、变更按钮、终端按钮的排列不重复的前提下,变更按钮是可复用的。以变更按钮最大化复用(即变更按钮或用于变更按钮的调车按钮数量最小化)为目标,设计变更按钮的最优化选择策略如下。 首先,为搜索空间Rd的轨道区段及调车,信号节点vx按以下方式赋予权值。 令初始权值We(vx)=0,对进路空间Rt中的每条变更进路R,若vx为调车信号,且vx∈Sg(R),则令权值We(vx)加1;若vx为轨道区段,且vx∈T(R),则令权值We(vx)加1。 然后,对于以上(1)、(2)所述问题,选择权值较大的一项即可。 以京张高铁全线11个车站(不含中继站、线路所及既有改造站)为例,对上述算法与策略进行验证。通过对本文算法生成的各站联锁表采用两级人工复查的方式进行检验,结果如表1所示。 表1 本文算法及量化策略指标算法指标检算 其中,进路遗漏率为未搜索出的合法进路数量与总进路数量之比;敌对遗漏率为敌对信号有遗漏的进路数量与总进路数量之比;敌对错误率为包含错误敌对信号(含敌对条件错误)的进路数量与总进路数量之比。 由表1可见,本文提出的算法、策略能够完整地搜索全站进路以及敌对信号,准确率较高。 以上测试均由设计人员根据信号设备平面布置示意图编制结构化的接口数据实现。设计效率可通过完善信号平面布置图的信息化辅助设计软件进一步提高。4 敌对信号搜索及敌对条件计算
4.1 敌对进路搜索

4.2 敌对信号搜索






5 其他算法与量化策略
5.1 关键道岔搜索算法
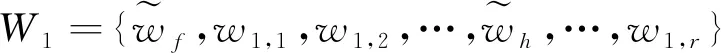
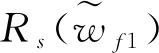
5.2 变更按钮选择的量化策略
6 结论与展望