软岩-混凝土界面剪切力变化规律及预测模型

李忠芳，舒 丹，王 姣，粟茜洁

(1.长江重庆航运工程勘察设计院，重庆 401147；2. 中设设计集团股份有限公司，南京 210014；3.重庆市水土保持监测总站，重庆 401147)

软岩的力学性能及其对港口工程混凝土嵌岩桩承载特性的影响相比于硬岩有较大的差异性[1-2]，软岩-混凝土桩界面(简称：岩-砼界面)的荷载传递特性会对桩基侧摩阻力的发挥造成影响[3-4]。研究外荷载作用下岩-砼界面的受力规律，建立合理的界面力学模型，这将有利于阐明软岩嵌岩桩的荷载传递模式并揭示其受力机理，具有重要的理论意义和工程应用价值。

剪切荷载作用下岩-砼界面的力学行为可充分反映桩基-软岩相互作用时桩侧摩阻力的发挥程度[5]。蒲诃夫[6]考虑了土体深度效应和桩-土相对滑移对桩-土界面荷载传递特性的影响，提出了改进的桩-土界面双曲线模型。蔡江东等[7]通过直剪试验，得出当桩周土强度较低时，桩侧摩阻力呈现出软化特征；当桩周土强度较高时，桩侧摩阻力呈现出硬化特征的结论。王建[8]通过现场试桩试验得出了3种典型的桩侧摩阻力与桩-土位移的变化规律：(1)非软化非硬化型：桩侧摩阻力随桩-土位移呈先增后平的趋势；(2)后期退化型：桩侧摩阻力-相对位移曲线呈现出由增到减到平的三折线规律；(3)后期硬化型：桩侧摩阻力-相对位移曲线分为2段，前期较陡、后期较缓。已有研究大都认为：桩-土界面的荷载传递规律以“非软化非硬化型”为主，且多采用双曲线函数表征其界面力学特征。然而，软岩和混凝土均属于硬质材料，其接触界面的受力特性理应更符合“后期退化型”的变化规律，因此软岩-混凝土界面的力学问题仍值得深入研究。

本文通过从工程现场取回软岩(中风化泥岩)试样，制备得到4组岩-砼试件，将之真空饱水后开展岩-砼界面剪切试验，实测得到饱和软岩-混凝土界面剪切力-位移曲线，分析岩-砼界面剪切力随位移的变化规律。在此基础上，根据桩侧摩阻力退化模型并结合试验数据回归得到模型中的计算参数，建立无因次化的岩-砼界面剪切力预测模型。

1 岩-砼界面剪切力变化规律

1.1 岩-砼界面剪切试验

本文采用RMT-301剪切试验系统来实施试验。根据该剪切试验系统的尺寸要求，制备得到4组岩-砼试件。其中，软岩、混凝土试件的尺寸分别为200×200×95 mm3、180×180×105 mm3。试件制作过程中，先将天然泥岩按上述标准打磨成型，再将其与C30混凝土一起浇筑成型，形成接触界面，经养护并饱水后得到饱和的岩-砼试件。试验步骤如下：

(1) 预热RMT-301系统，将已制备好的岩-砼试件放入下剪切盒中，砼侧在下，岩侧在上。

(2) 安放上剪切盒，在岩侧表面均匀洒抹一层5～10 mm厚的细沙并盖上一块与试件等长、等宽的钢板，将试件及上、下剪切盒推送至剪切试验区域。

(3) 在下剪切盒的销轴上套上水平拉杆，由于RMT-301剪切系统的法向应力加载臂的长度有限，故应在上剪切盒的正上方放置钢垫块；同时，为避免因法向应力加载臂与钢垫块之间发生较大的滑动摩擦，在最上层钢垫块处设置滚柱，以滚动摩擦来代替滑动摩擦，减小试验误差；

(4) 在系统配套的计算机上设置各项基本参数，进行竖向、水平预加载。而后，按照所设置的加载速率对试件施加竖向力(本文共计对4组饱和岩-砼试件分别施加25、40、60、80 kN的竖向力)，待竖向力施加完成后，即可通过拉杆对下剪切盒施加水平剪切力，采用上、下剪切盒之间的相对位移(即岩-砼界面的位移)作为判断标准，当该位移达到某一值时，表明试件的界面已发生破坏，此刻停止加载。

1.2 岩-砼界面剪切力-位移曲线

如图1所示，为当竖向力P分别为25、40、60、80 kN时岩-砼界面的剪切力随位移的变化曲线。从中可以看出：随着岩-砼界面位移的增加，界面剪切力呈现出“先增、后减、终平”的变化规律，即：岩-砼界面剪切力先随位移的增加呈现出非线性的增大趋势；当位移达到某一值时(图1中显示约2.6 mm)，界面剪切力达到峰值；接下来，界面剪切力随位移的增加而逐渐降低最终趋于平稳，此时的剪切力被称之为残余剪切力。另一方面，界面剪切力的实测结果随竖向力的增加而逐渐增大。综上表明：饱和软岩-混凝土界面的力学特性与“后期退化型”的变化规律相吻合。

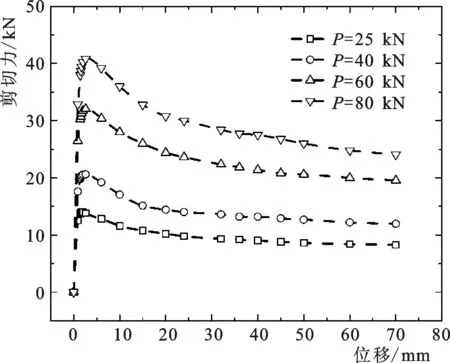
图1 岩-砼界面剪切力-位移曲线Fig.1 Shear force vs. displacement curve for rock-concrete interface

2 岩-砼界面剪切力预测模型

为了定量描述岩-砼界面剪切力随位移的变化规律，预测不同竖向力作用下岩-砼界面的剪切力数值大小，本文基于桩侧摩阻力退化模型的数学表达式，根据试验结果确定其计算参数，建立无因次化的岩-砼界面剪切力预测模型并验证模型的正确性。

2.1 桩侧摩阻力退化模型

根据文献[9-10]，桩侧摩阻力退化模型的一般数学表达式可写为

(1)

式中：Fτ为桩侧摩阻力，本文中即表示岩-砼界面剪切力，kN；x为桩-土之间的相对位移，本文中即表示岩-砼界面位移，mm；a、b、c分别为计算参数。式(1)的函数表达式能够有效描述岩-砼界面的剪切力随位移变化的“先增、后减、终平”趋势。此外，模型式(1)仅能用于表征在竖向荷载作用下桩侧摩阻力随桩-土相对位移的变化特征，不可用于描述水平荷载作用下桩身截面横向剪切力的变化规律。

2.2 模型建立

为了让建立得到的预测模型普适性更强，将式(1)中的岩-砼界面剪切力Fτ及位移x这两个自变量进行无因次化处理，得到无因次化的岩-砼界面剪切力和位移，即：Fnτ=Fτ/P，xn=x/xmax。其中，P为在试验过程中作用在岩-砼试件上的竖向力，P=25、40、60、80 kN；xmax为峰值剪切力对应的岩-砼界面位移，根据图2可知：xmax=2.6 mm。将Fnτ、xn带入式(1)中，可得到桩侧摩阻力退化模型的无因次化数学表达式

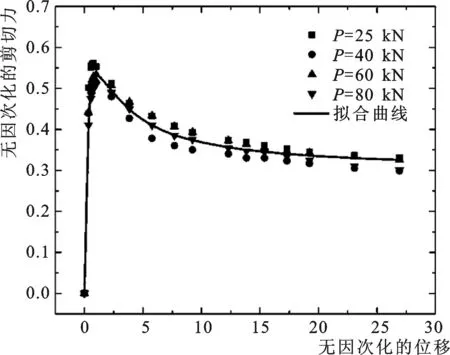
图2 岩-砼界面无因次化剪切力散点及其拟合曲线Fig.2 Normalized shear force scatters of rock-concrete interface and its fitted curve

(2)

式中：a′、b′、c′分别为式(2)中的计算参数。根据Fnτ、xn的表达式并结合图1中的试验结果，绘制得到无因次化的岩-砼界面剪切力散点随无因次化岩-砼界面位移的变化图示，如图2所示。基于式(2)的函数型式并结合非线性回归方法，可拟合得到式(2)中的计算参数a′=0.378、b′=0.091、c′=0.553，拟合曲线详见图2。因此，基于桩侧摩阻力退化模型一般表达式的无因次化岩-砼界面剪切力预测模型可写为

(3)

2.3 模型验证

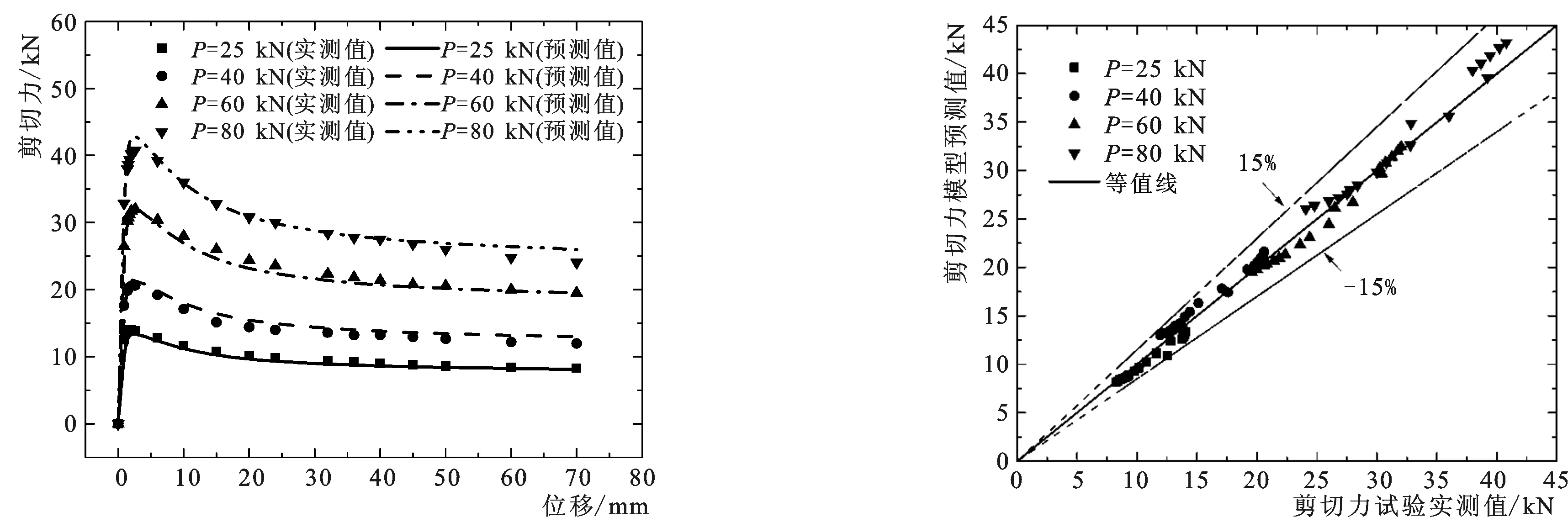
为了验证式(3)中模型预测值的正确性，文中将不同竖向力P作用下通过剪切试验实测得到的岩-砼界面剪切力的结果(简称：试验实测值)同式(3)中预测模型的计算值(简称：模型预测值)二者进行对比分析，结果见图3。从图中可知：岩-砼界面剪切力的模型预测值不论从数值大小亦或是变化趋势上均与试验实测值的吻合程度高。此外，文中也绘制得到岩-砼界面剪切力试验实测值与模型预测值的误差分析图，见图4。从中可明显观察到：基于式(3)的岩-砼界面剪切力模型预测值与试验实测值二者均包含在±15 %的相对误差范围内，证明了式(3)预测结果的精度。

3 结论

本文通过开展饱和软岩-混凝土界面剪切试验研究，详细分析了岩-砼界面剪切力随位移的变化规律，建立了无因次化的岩-砼界面剪切力预测模型，结论如下：(1) 随着岩-砼界面位移的增加，界面剪切力呈现出“先增、后减、终平”的变化规律，饱和软岩-混凝土界面的力学特性符合桩侧摩阻力的“后期退化型”特征；(2) 根据试验结果确定了桩侧摩阻力退化模型一般数学表达式中的计算参数a′=0.378、b′= 0.091、c′=0.553，建立无因次化的岩-砼界面剪切力预测模型；(3) 经对比分析，岩-砼界面剪切力的模型预测值与试验实测值二者之间的相对误差在±15 %的范围内，验证了预测模型的正确性。