填充墙竖向不规则布置RC 框架结构考虑SSI 效应的MPA 分析

2020-07-27陈大川湛洋王海东刘举

湖南大学学报（自然科学版） 2020年7期

陈大川，湛洋，王海东，刘举

（湖南大学土木工程学院，湖南长沙410082）

静力弹塑性（Pushover）方法由于其概念简洁、操作简便和计算高效的特点，在实际工程中得到广泛应用.Chopra 等[1]从结构动力学基本原理出发，考虑高阶振型和结构屈服后惯性力重分布对结构地震反应的影响，提出概念简单、运算简洁的模态Pushover方法，提高了计算精度.MPA 方法能够确定结构在罕遇地震下潜在的破坏机制，找到相应的薄弱环节，从而使设计者可以对局部薄弱环节进行加强，使整体结构达到预定的使用功能，在实际工程中得到广泛应用.

黄华等[2]通过对29 个框架填充墙模型进行地震分析，指出随着薄弱层的位置不同，填充墙对框架抗侧移刚度的参与率不同，同时提出了采用截面面积比来评定薄弱层的经验方法.刘举[3]指出对于底层为空框架的RC 框架填充墙结构，考虑SSI 和填充墙刚度效应的结构倒塌时变形主要集中在结构的底部两层，致使框架结构的耗能能力明显减弱，表现出类似薄弱层的效应.Daniele 等[4]从不同角度研究填充墙对结构周期响应的影响，分析不同高度的结构模型，提出了一个新的线性结构周期响应规律.Konstantinos 等[5]通过对比纯框架、框架填充墙结构在连续地震作用下的地震响应，发现框架填充墙结构地震响应会更大.黄靓等[6]通过对比带节能砌体填充墙的RC框架与纯框架的试验结果，指出填充墙的存在使得框架结构的强度和刚度退化加快，但却表现出较强的抗倒塌能力.

传统的模态Pushover 分析方法（MPA）是建立在刚性地基假定条件下的，当需要考虑SSI 效应时，传统的MPA 不再适用.Galal 等[7]指出在考虑SSI 效应时结构的抗震需求与刚性地基假定时存在明显差异.Rajeev 等[8]指出高层结构进入非线性状态时，结构变柔，SSI 效应的影响更加显著.岳庆霞等[9]指出考虑SSI 效应结构变柔，结构的顶层位移增加，抗倒塌能力降低.王海东等[10]指出地震作用下考虑重力二阶效应与SSI 效应之后，塑性铰主要集中在结构的底部楼层，变形集中效应明显.

本文通过周期等效原则，提出考虑SSI 的MPA方法，并对其进行验证.以一10 层带竖向不规则填充墙的RC 框架结构为研究对象，调整层间刚度比和“薄弱层”的布置位置，运用此方法分析该类结构在不同场地和设防烈度条件下的地震响应规律，为带填充墙的RC 框架设计提供参考.

1 考虑SSI 效应的MPA 方法研究

传统模态Pushover 分析方法（MPA）通过将多自由度结构等效成多个不耦连的等效单自由度体系，并求解这些等效单自由度体系的最大变形Dn来计算结构的反应[1].

然而，传统MPA 方法是建立在刚性地基假定下的，并未考虑SSI 效应.下面给出考虑SSI 效应的MPA 方法，并对此方法进行简单的验证.

1.1 弹性阶段考虑SSI 效应的MPA 基本原理

本文依据ATC40 和FEMA440 中的简化方法，采用土弹簧模型来模拟土对结构的作用，即通过在基础上施加水平、竖直以及绕轴方向的弹簧来模拟地基土对基础的约束，3 个弹簧对应刚度Kx、Kz和Kθy具体计算方法参照文献[3].

当考虑SSI 效应时，多层结构在水平地震作用下的微分方程见式（1）[11].

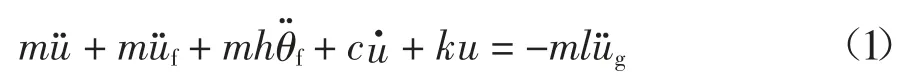
式中：u 为上部结构相对基础的水平位移向量；uf和θf分别为基础相对于地基的水平位移和转动；m 为上部结构的质量矩阵；c 为阻尼矩阵；k 为侧移刚度矩阵.

利用模态之间的正交性，令

式中：φn为结构n 阶模态；qn为结构模态位移；un（t）是结构在n 阶模态下的水平位移；Γn是n 阶模态参与系数；Dn（t）是等效单自由度体系的位移.

将式（2）、式（3）代入式（1）可得考虑 SSI 效应时n 阶模态体系振动微分方程：

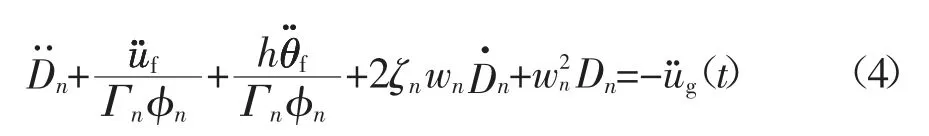
式中：wn是刚性地基假定下上部结构的振动频率；ζn是第n 阶阵型阻尼比.

第n 阶模态体系的近似基本周期为[11]：

式中：Tnssi为考虑SSI 效应时第n 阶模态体系的近似基本周期；Tns为不考虑SSI 效应时第n 阶单自由度体系的周期；Tnx为水平弹簧Kx引起的周期增量；Tnθ为绕轴弹簧Kθy引起的周期增量；Mn为结构第n 阶模态质量；Kn为不考虑SSI 效应时第n 阶单自由度体系的刚度；h 为结构质量中心的高度.需要说明的是，由于分析的是结构在水平地震动作用下的响应，没有涉及竖向地震动，这里忽略了竖向弹簧Kz的影响.

综合式（5）（6）（7）（8），可得：

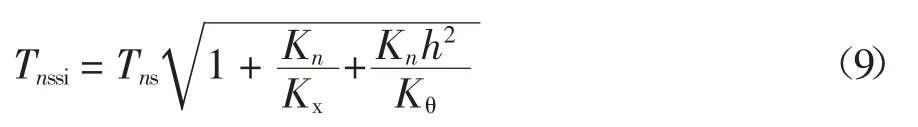
为了求出方程（4）的解Dn（t），建议采用周期等效法，将式（4）对应的振动体系等效成周期等于Tnssi（即Tne=Tnssi）的单自由度振动体系，如图1 所示，从而求解式（4）中的Dn（t），并以此完成考虑SSI 效应的MPA 分析.应用此方法，结构的每一阶阵型均可等效成一个独立的单自由度体系，考虑了高阶振型对结构响应的影响，提高了计算精度.

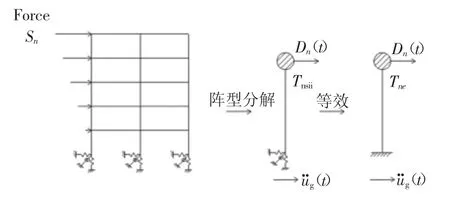
图1 考虑SSI 的弹性多自由度结构的MPA 分析过程Fig.1 MPA analysis process considering elastic multi-degree-of-freedom structure of SSI

1.2 弹塑性阶段考虑SSI 效应的MPA 基本原理

当一个构件进入到弹塑性阶段时，由于塑性变形的存在，在循环往复荷载作用下，构件受到的力和位移不再是一一对应关系，而是形成滞回曲线.也就是说，当构件进入弹塑性阶段时，力和位移的值取与变形发展的过程有关.

对于进入到弹塑性阶段的多自由度振动体系，其侧向力和位移的关系表达式变为：

将式（10）代入式（1）有：

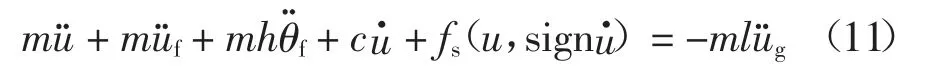
式（2）对应的是弹性阶段第n 阶阵型对应的阵型位移，当结构进入非线性阶段时放大线性阶段的阵型位移可得到弹塑性阶段的阵型位移，如式（12）所示.

将式（12）代入式（11）中，结合式（3）可得：

式中：Dn（t）为第n 阶阵型对应考虑SSI 效应的单自由度体系的位移.

要求解式（13），必须通过式（14）得到 Fsn/Ln和Dn的关系，而这个关系一般情况下无法得到解析解，必须依靠有限元分析软件，具体过程如下：

对结构逐步施加阵型荷载至结构倒塌或失效，绘制基底剪力Vbn-顶点位移urn曲线（Pushover 曲线），并通过等能量原理简化为双折线.按下式将双折线转化为Fsn/Ln和Dn的关系曲线：

至此，即可求得Dn，继而求得un，利用SRSS 法计算多阶阵型作用时总的水平位移umax，即

1.3 考虑SSI 效应的MPA 方法的验证分析

1.3.1 模型介绍

本文采用与文献[3]相同的计算模型，为10 层RC 框架结构，跨度为5 m，底层层高3.9 m，其他层层高3.6 m，图2 所示为其平、立面图，表1 列出了梁、柱基本设计参数，图3 给出了梁柱截面配筋图.柱的混凝土强度等级为C40，梁、板的混凝土强度等级为C35，钢筋采用HRB400，纵筋配筋情况见表1，梁箍筋直径10 mm，间距150 mm，板厚100 mm，钢筋混凝土自重为25 kN/m3.在模拟分析中，选择中间一榀框架进行分析，混凝土本构模型选用Mander 模型，钢筋本构模型选用Park 模型；梁柱均使用集中塑性铰模型，在距离梁端分别为0.1 和0.9 倍梁长处布置考虑弯矩的M3 铰；在距离柱端分别为0.1 倍和0.9倍柱长处布置考虑轴力与弯矩相互作用的P-M2-M3 耦合铰.

为方便表述，在后文中以本节介绍的模型为基础，刚性地基假定条件下，不考虑填充墙刚度效应的模型简称模型M；考虑SSI（三类场地土）时，不考虑填充墙刚度效应的模型简称模型N.

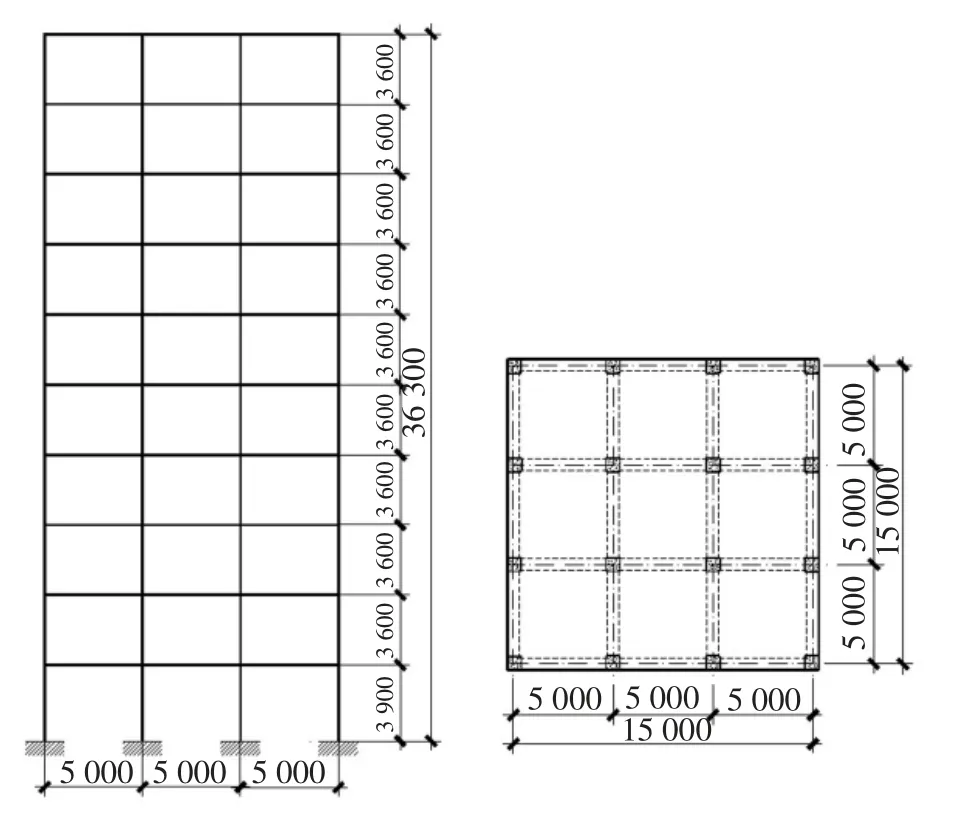
图2 平、立面布置图（单位：mm）Fig.2 Plane and elevation layout（unit：mm）

表1 框架梁、柱截面Tab.1 Section table of frame beams and columns

1.3.2 SSI 效应的实现

本文采用柱下独立基础，基础尺寸4 m×4 m，厚度为1 m，埋深为1.8 m，采用ATC40 和FEMA440 推荐的土弹簧模型来模拟地基对结构的作用.土弹簧简化模型选用ATC40 中的简化模型，如图3 所示；土弹簧简化模型的部分刚度计算公式如表2 所示；不同场地土体的具体参数如表3 所示.

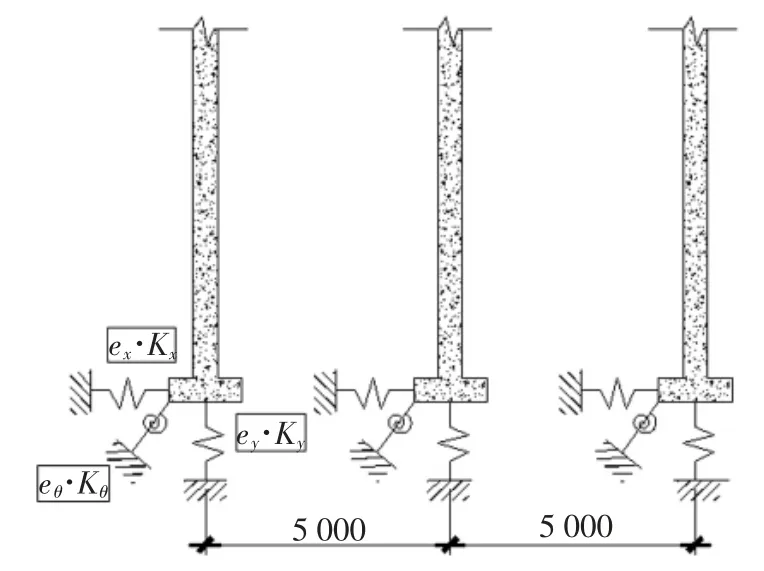
图3 土弹簧模型（单位：mm）Fig.3 Soil spring mode（unit：mm）

表2 土弹簧刚度公式及深度修正系数表Tab.2 Expressions for spring stiffness and their embedment factors

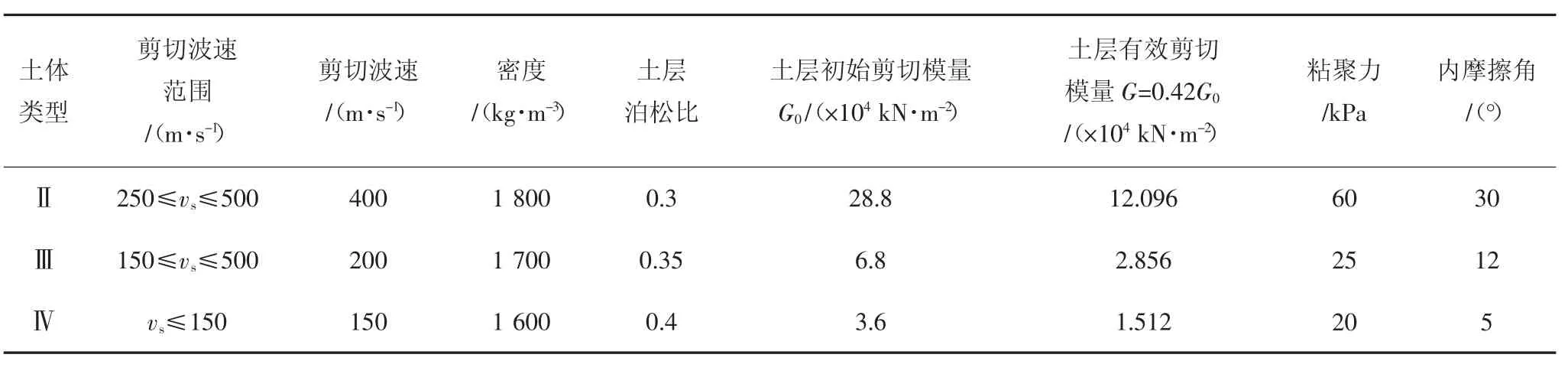
表3 土体参数表Tab.3 Soil parameters

1.3.3 填充墙的实现

本文研究填充墙对框架结构整体的影响，采用对角受压斜撑有限元模型来模拟填充墙[12]，其具体简化模型如图4 所示.

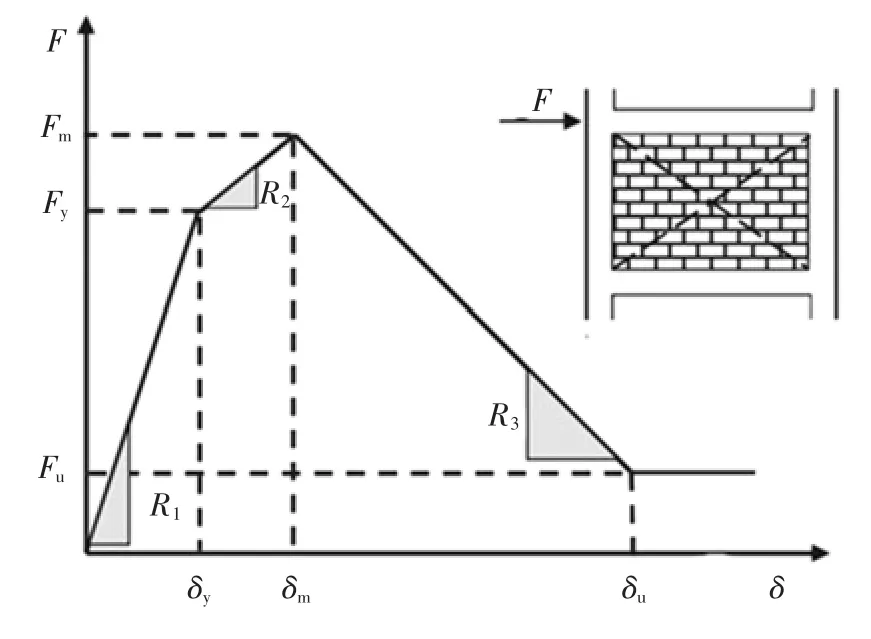
图4 填充墙的斜压杆模型[12]Fig.4 Compression strut model of infilled wall[12]

剪切模量与弹性模量相关，填充墙抗压强度与弹性模量相关[13]：

式中：初始刚度为R1；屈服刚度为R2；软化刚度为R3；屈服力为 Fy；极限力为 Fm；残余力为 Fu；Gm为填充墙的剪切模量；Em为填充墙的弹性模量；fms为填充墙的抗剪强度；lm、hm和tm分别为填充墙的长度、高度和厚度；bm是压杆等效宽度；dm是填充墙对角线长度.

刚度和屈服力均只与填充墙的弹性模量和物理尺寸有关，故本文通过不断调整Em的大小来改变填充墙的刚度和强度，得到不同大小的层间刚度比，以此来模拟不同种类填充墙对于结构抗震性能的影响.

1.3.4 验证结果

本文对上述考虑SSI 效应的MPA 可行性进行验证：在设防烈度7 度条件下，对RC 框架填充墙结构（在模型N 的基础上在2～10 层加入填充墙，调整值使一二层刚度比为1.4）分别进行考虑SSI 效应（Ⅲ类土）的MPA 分析和时程分析，各阶模态参数如表4 所示.

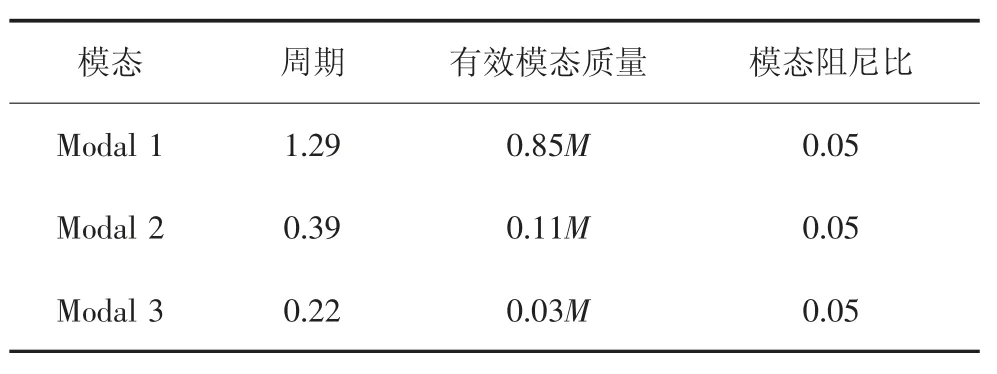
表4 各阶模态参数Tab.4 Modal parameters of each order

考虑到时程分析的不确定性，结构的地震响应与场地土特征、结构自身特性以及地震动输入选取有关，因此必须保证地震波选取的合理性.Northbridge、San Fernando 和 Northbridge 3 条地震波的反应谱均值与设计反应谱在统计意义上相符[3]，因此选用这3 条地震波进行时程分析，结果采用3 条地震波作用下的平均结果来讨论.多遇地震和罕遇地震下结构的层间位移角分布如图5 所示，表5 给出了时程分析与考虑SSI 的MPA 对比分析得到的结构层间位移角误差.

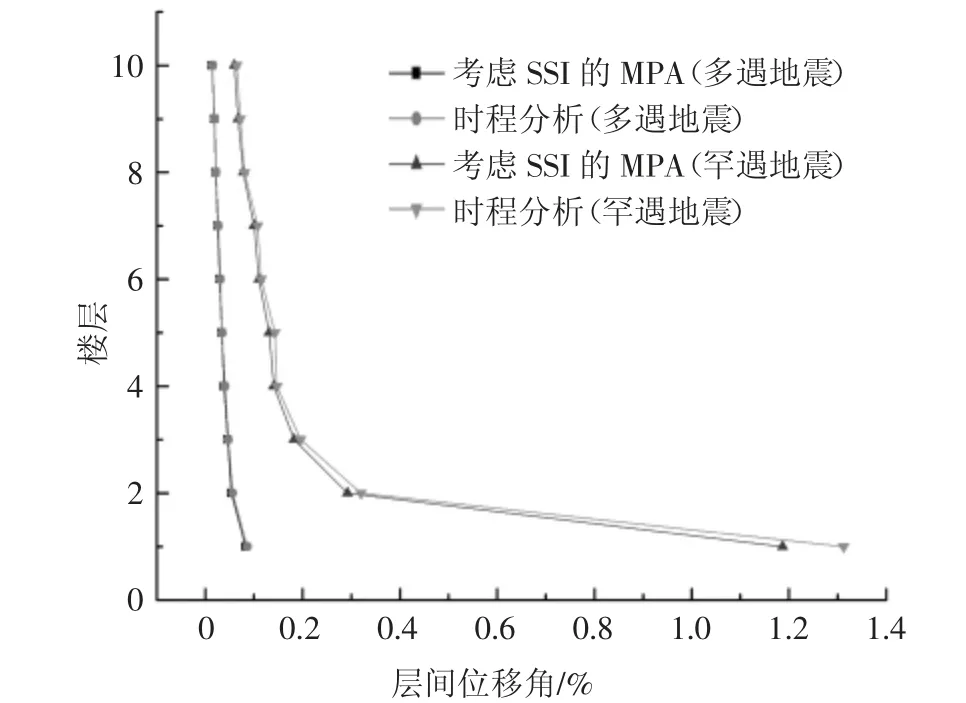
图5 多遇地震和罕遇地震下结构的层间位移角分布Fig.5 Inter-layer displacement angular distribution of structures under frequent earthquakes and rare earthquakes

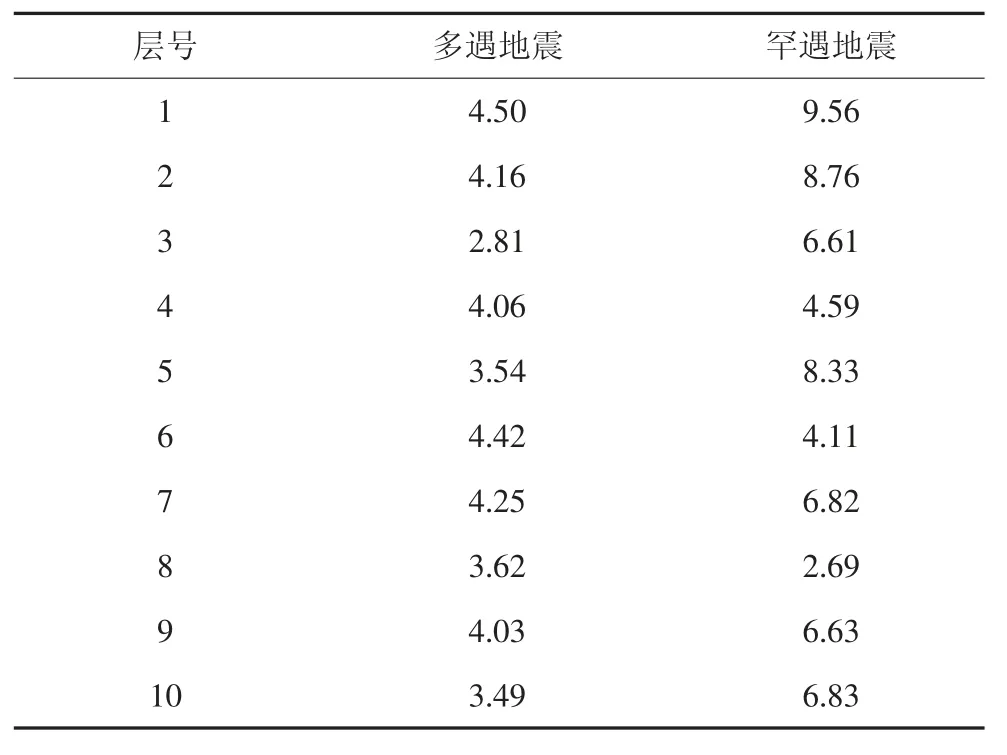
表5 结构层间位移角误差Tab.5 Structural interlayer displacement angle error %

从图5 和表5 可看出，多遇地震作用下，结构最大层间位移角误差为4.50%；罕遇地震作用下，结构最大层间位移角误差为9.56%.说明在结构处于弹性状态与弹塑性状态时，考虑SSI 的MPA 分析结果与时程分析结果基本一致，此简化方法可行.

2 层间刚度比对填充墙框架结构响应的影响分析

2.1 反应谱分析

反应谱分析方法通过振型分解的方法计算结构在弹性阶段的动力响应，为了说明弹性状态下结构响应规律，本文对模型M、N 进行反应谱分析.图6、图7 给出了其中模型M、N 的层间位移角，表6 列出了反应谱分析下不同模型的最大层间位移角.

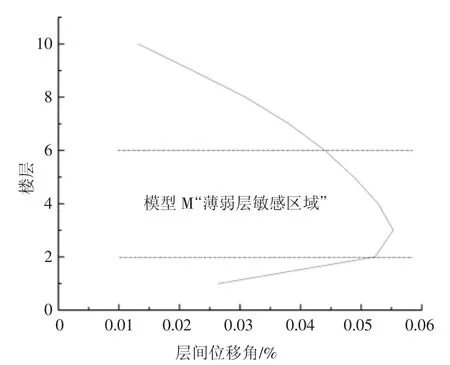
图6 模型M 层间位移角分布Fig.6 Inter-layer displacement angle distribution of model M

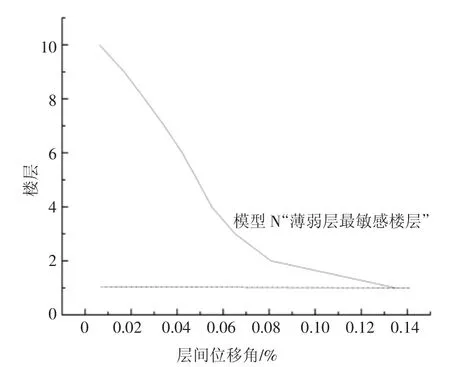
图7 模型N 层间位移角分布Fig.7 Inter-layer displacement angle distribution of model N

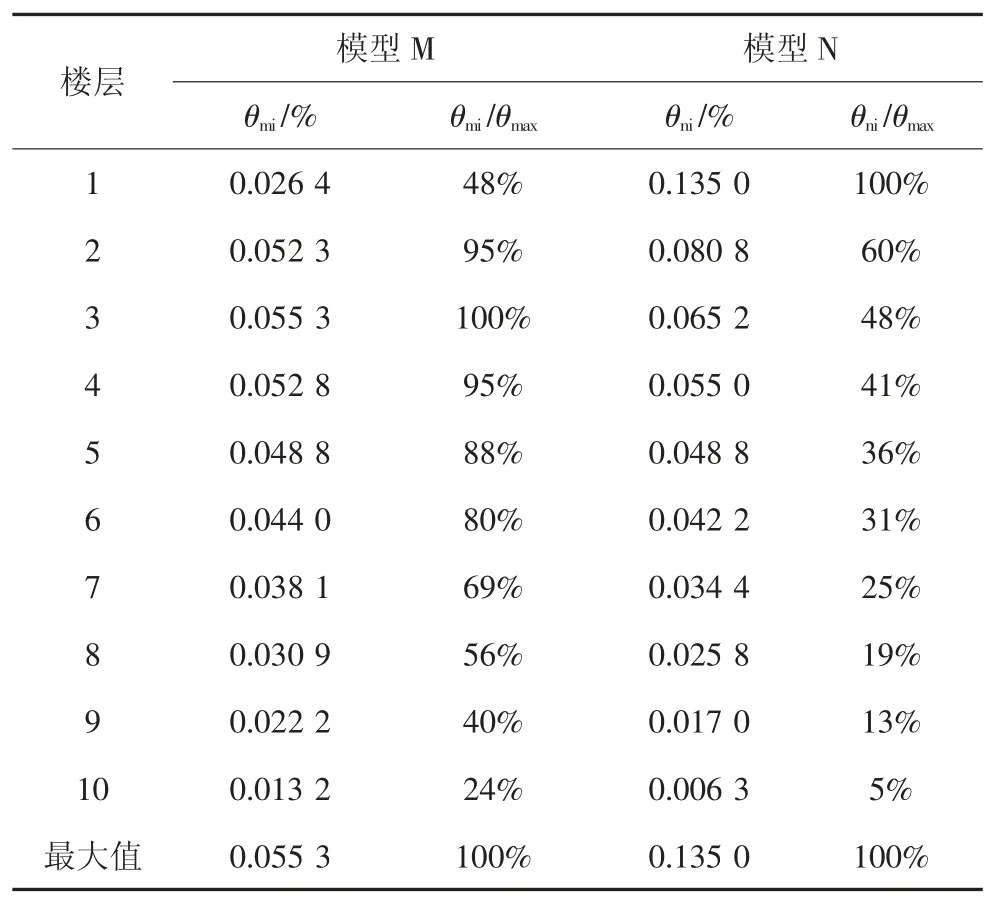
表6 反应谱工况模型M、N 各楼层的层间位移角及比值Tab.6 Inter-layer displacement angle and ratio of each floor of response spectrum model M and N

本文研究填充墙不均匀分布对结构抗震性能的影响，若某一层没有布置填充墙而其他层均布满填充墙，则将没有布置填充墙的这一层定义为“薄弱层”.为了方便研究结构进入弹塑性状态时薄弱层的位置对结构地震响应的影响，根据文献[3]将反应谱分析中层间位移角超过最大层间位移角75%的楼层区域称为“薄弱层敏感区域”，以模型M 为例，即2～6层区域；将反应谱分析中层间位移角最大的楼层称为“薄弱层最敏感楼层”，以模型M 为例，即第3 层，如图6、图7 所示.

下文将根据“薄弱层”布置位置与“薄弱层最敏感楼层”的关系在罕遇地震烈度下进行层刚度比对结构响应的影响分析，分3 种工况展开：

工况1：考虑SSI 效应，“薄弱层”布置位置与“薄弱层最敏感楼层”相同；

工况2：考虑SSI 效应，“薄弱层”布置位置与“薄弱层敏感区域”不同.

工况3：刚性地基假定下，“薄弱层”布置位置与“薄弱层最敏感楼层”相同.

2.2 工况1 结构响应分析

模型N 的“薄弱层最敏感楼层”在第1 层，故将“薄弱层”布置在第1 层，通过不断调整填充墙刚度来调整层刚度比，对不同层刚度比结构模型进行MPA 分析.层间刚度比变化范围为1.0～2.0，变化率为0.1，直到最大层间位移角超过1/50.

本节选择考虑SSI 效应（三类场地土）和填充墙刚度效应的结构模型来研究“薄弱层”位于底层时“薄弱层”与其上一层的层刚度比对结构响应的影响.

图8、图9、图10 分别给出了设防烈度为7 度、8度、9 度时各楼层层间位移角分布.

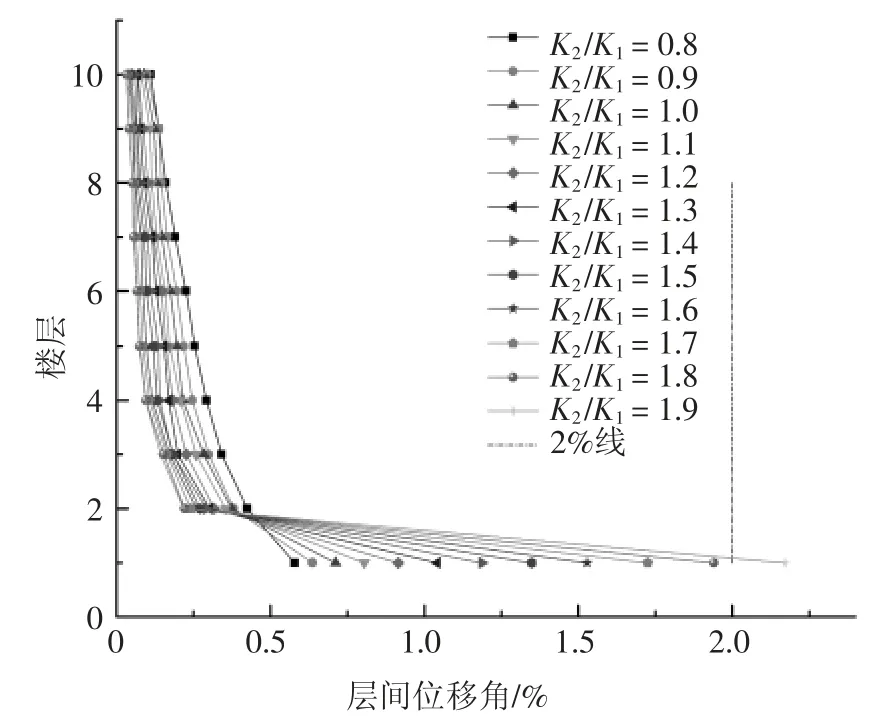
图8 7 度设防各楼层层间位移角分布Fig.8 Inter-layer displacement angle distribution between layers of seven degrees

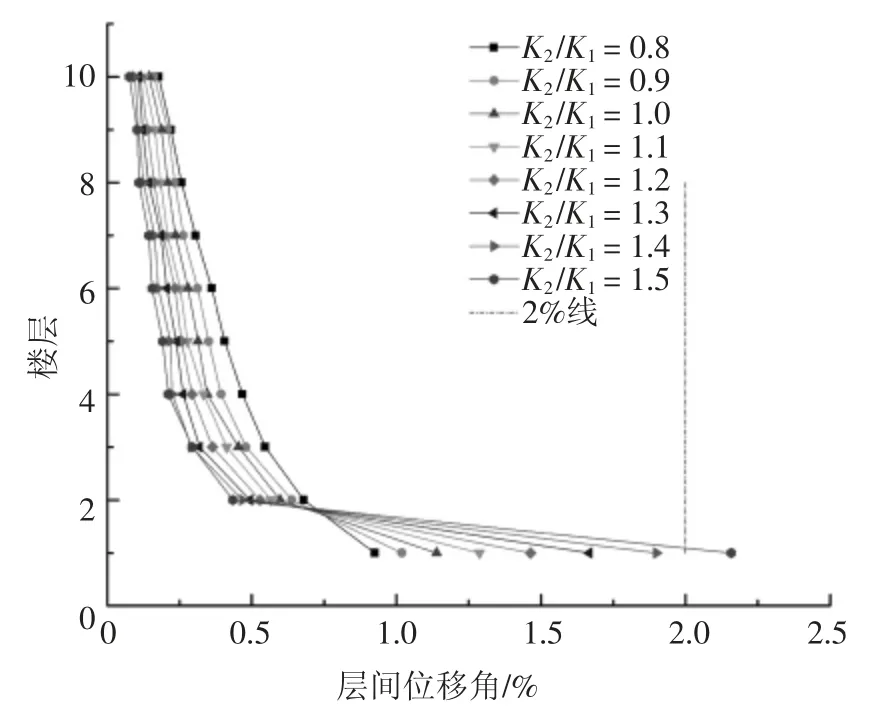
图9 8 度设防各楼层层间位移角分布Fig.9 Inter-layer displacement angle distribution between layers of eight degrees

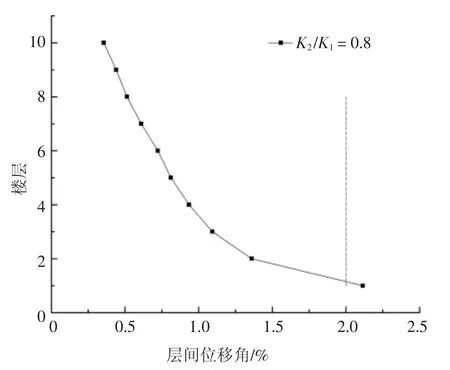
图10 9 度设防各楼层层间位移角分布Fig.10 Inter-layer displacement angle distribution between layers of nine degrees

图11 给出了在不同地震烈度条件下将“薄弱层”设置在“薄弱层最敏感楼层”时最大层间位移角达到文献[14]规定的罕遇地震下弹塑性层间位移角限值1/50 时对应的层间刚度比.对比分析图8、图9、图10 以及图11 可知：

1）同一设防烈度下，结构的最大层间位移角均出现在结构“薄弱层”处，且“薄弱层”处的层间位移角随层刚度比增大变大，变形向“薄弱层”处集中.非“薄弱层”楼层的层间位移角则随层刚比增大变小.

2）不同设防烈度下，7 度设防，层刚度比为1.9时结构最大层间位移角超过1/50；8 度设防，层刚度比为1.5 时结构最大层间位移角超过1/50；9 度设防，层刚度比为1.0 时结构最大层间位移角超过1/50.这表明在考虑SSI 效应后，结构达到弹塑性层间位移角限值时对应的层间刚度比随设防烈度增高变小.

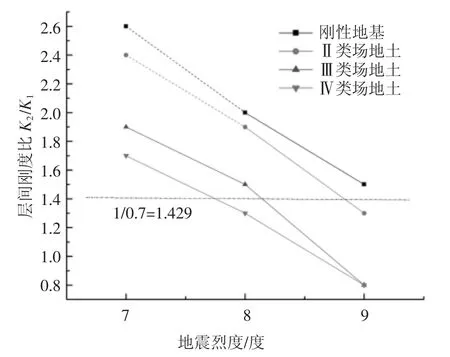
图11 层间位移角达到限值1/50 时对应的层间刚度比Fig.11 Corresponding interlayer stiffness ratio when the interlayer displacement angle reaches the limit of 1/50

3）文献[14]规定RC 框架结构层刚度比不得小于0.7，即层刚度比不得大于1.429，如图9 所示.8 度设防在Ⅳ类场地上、9 度设防在Ⅱ类、Ⅲ类和Ⅳ类场地上，结构在层间位移角超限时相应的层间刚度比均小于1.429，说明在考虑SSI 效应和填充墙竖向不规则布置后，层刚度比小于1.429（即大于0.7）不一定安全.且同一设防烈度下，场地土越软，层间位移角超限的层刚度比越低.

2.3 工况2 结构响应分析

模型N 的“薄弱层敏感区域”在1 层，现将“薄弱层”布置在第2 层，通过不断调整填充墙刚度来调整层刚度比对结构模型进行MPA 分析，研究薄弱层布置在非“薄弱层敏感区域”时层刚度比对结构响应的影响.层间刚度比变化范围为1.0～2.0，变化率为0.1，直到最大层间位移角超过1/50.

本节选择考虑SSI 效应（三类场地土）和填充墙刚度效应的结构模型来研究“薄弱层”位于2 层时“薄弱层”与其上一层的层刚度比对结构响应的影响.

图12 给出了9 度设防各楼层层间位移角分布.

通过图表分析可知：

1）当层刚度比等于1.0 即结构为没有填充墙的裸框架时，最大层间位移角超过1/50；当加入填充墙且层刚度比在1.1～2.0 范围变化时，结构层间位移角没有超过1/50，且随层刚度比增大，结构的响应趋势逐渐减小，填充墙对限制结构层间位移角存在明显有利的影响.这表明在“薄弱层敏感区域”以外的楼层布置“薄弱层”不会使结构形成明显的薄弱层.

2）当“薄弱层”与“薄弱层最敏感楼层”不是同一楼层时，随层间刚度比值增大，最大层间位移角所在的楼层会逐渐由“薄弱层最敏感楼层”向“薄弱层”过渡.建议设计人员注重对这些过渡楼层的层间位移角评估.

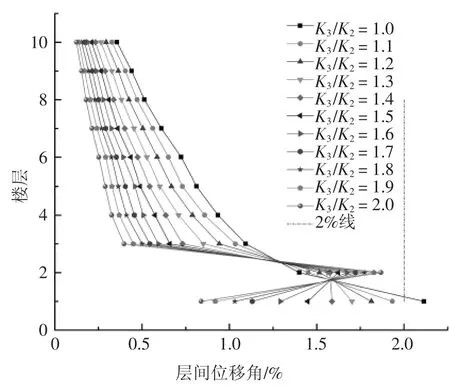
图12 9 度设防各楼层层间位移角分布Fig.12 Inter-layer displacement angle distribution between layers of nine degrees

2.4 工况3 结构响应分析

模型M 的薄弱层最敏感楼层在第3 层，故将“薄弱层”布置在第3 层，通过不断调整填充墙刚度来调整层刚度比对结构模型进行MPA 分析.层间刚度比变化范围为1.0～2.0，变化率为0.1，直到最大层间位移角超过1/50.

本节选择刚接状态下考虑填充墙刚度效应的结构模型来研究将“薄弱层”布置在第3 层时层间刚度比对结构响应的影响，因第2 层和第4 层侧向刚度相同，故取第2 层分析.

图13、图14、图15 分别给出了设防烈度为7度、8 度、9 度时各楼层层间位移角分布.表7 给出了第2、3 层间位移角变化幅度.

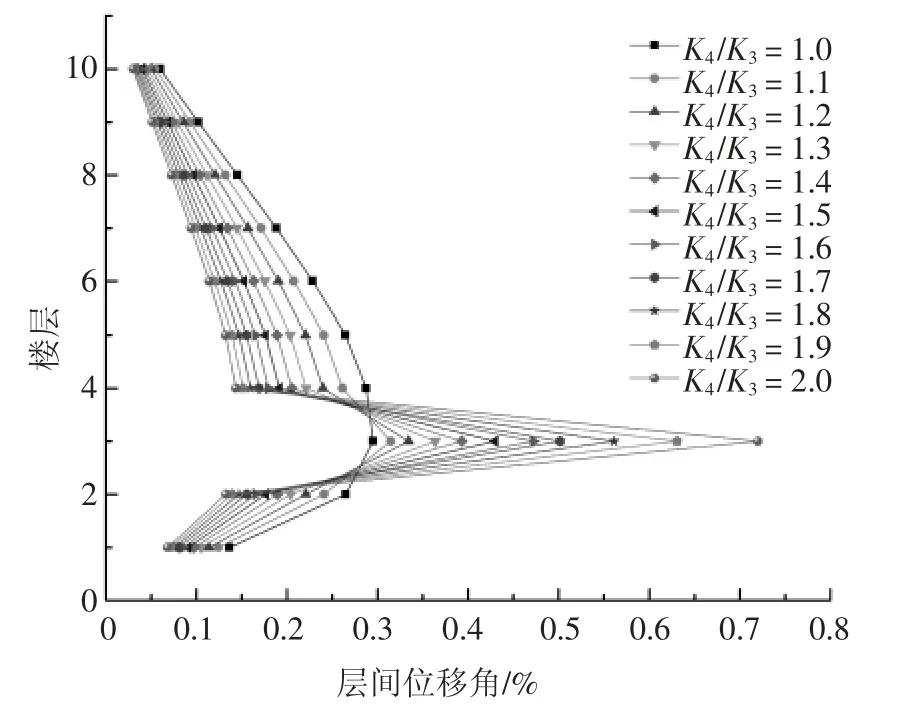
图13 7 度设防各楼层层间位移角分布Fig.13 Inter-layer displacement angle distribution between layers of seven degrees

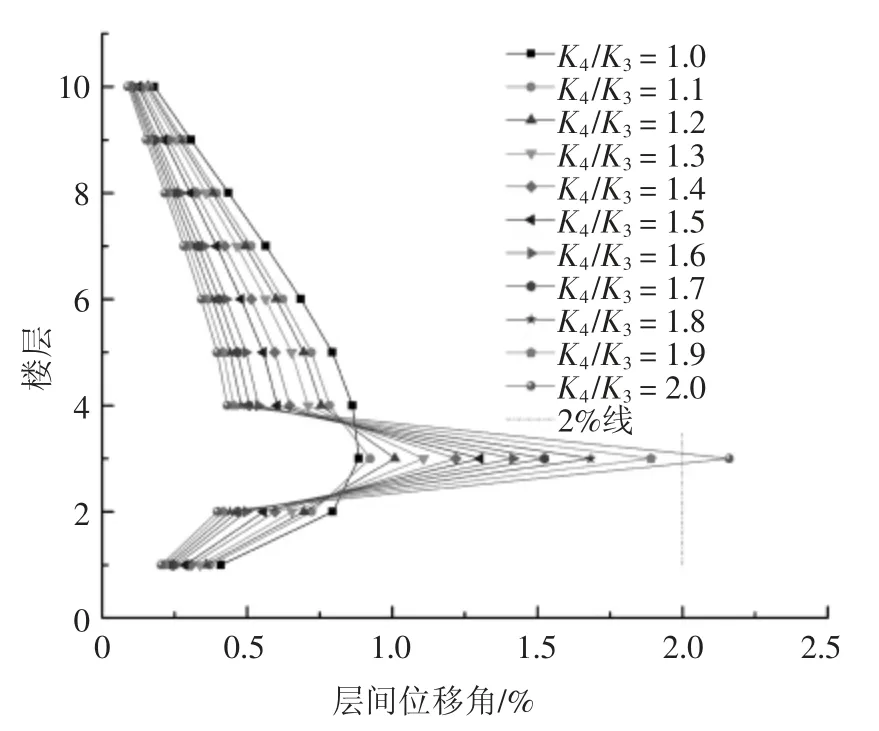
图14 8 度设防各楼层层间位移角分布Fig.14 Inter-layer displacement angle distribution between layers of eight degrees

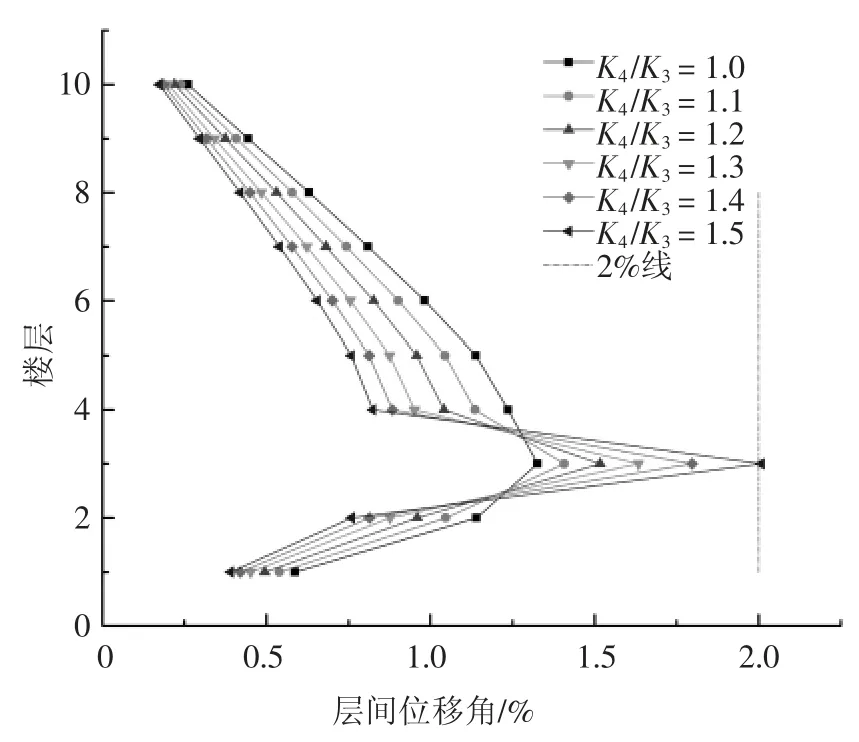
图15 9 度设防各楼层层间位移角分布Fig.15 Inter-layer displacement angle distribution between layers of nine degrees

通过分析图13、图14、图15 和表7 可知：

1）同一设防烈度下，结构“薄弱层”处的层间位移角分布会出现凸起，且层刚度比越大凸起程度越大，这样的凸起主要是由于“薄弱层”处出现刚度突变，地震作用下变形向“薄弱层”处集中，对结构造成明显的不利影响.非“薄弱层”楼层的层间位移角则随层刚比增大变小.

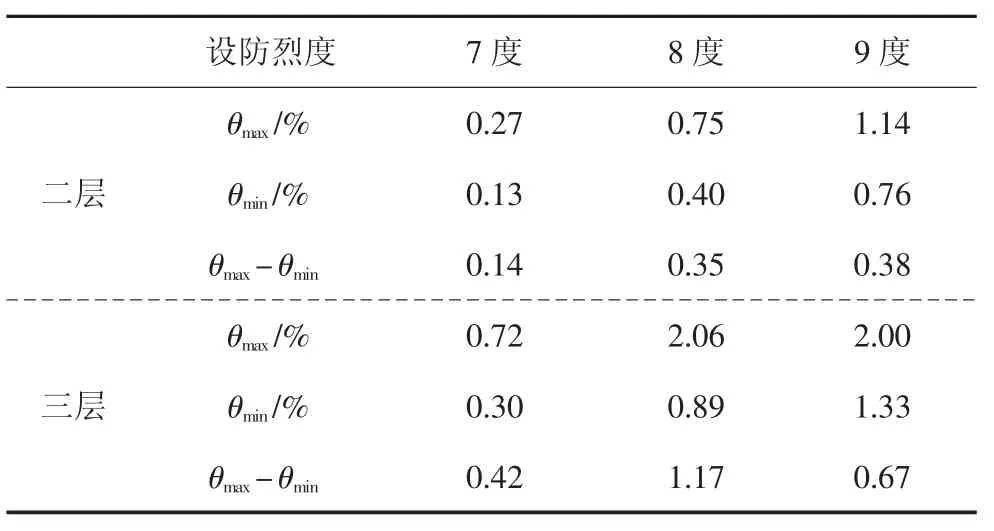
表7 二、三层间位移角变化幅度Tab.7 Variation range of inter-layer displacement angle between the second and third layers

2）不同设防烈度下，7 度设防，层刚度比在1.0～2.0 区间变化时结构最大层间位移角均未超过1/50，满足我国现行规范中“大震不倒”的要求；8 度设防，层刚度比大于等于2.0 时结构最大层间位移角超过1/50；9 度设防，层刚度比大于等于1.5 时结构最大层间位移角超过1/50.结构达到弹塑性层间位移角限值时对应的层间刚度比随设防烈度增高变小.

2.5 框架梁柱及填充墙的破环情况

图16 和图17 给出了罕遇地震设防烈度8 度，层间刚度比1.4，“薄弱层”与“薄弱层最敏感楼层”位置相同时，结构前三阶模态梁柱塑性铰分布及填充墙非线性发展情况.从图中可以看出，主体结构的塑性铰和进入非线性状态的填充墙主要分布在“薄弱层”附近.填充墙的非线性发展程度和破坏程度要高于梁柱构件，在结构抗震中起到了第一道防线的作用.

对比工况1、工况2 和工况3 的分析可知：当“薄弱层”与“薄弱层最敏感楼层”位置相同时，层刚度比的增大会放大“薄弱层”层间位移角，使“薄弱层”更薄弱，对结构造成明显的不利影响；当“薄弱层”与“薄弱层最敏感楼层”位置不同时，随层刚比增大，“薄弱层”层间位移角增加不明显，不会形成明显的薄弱层效应.

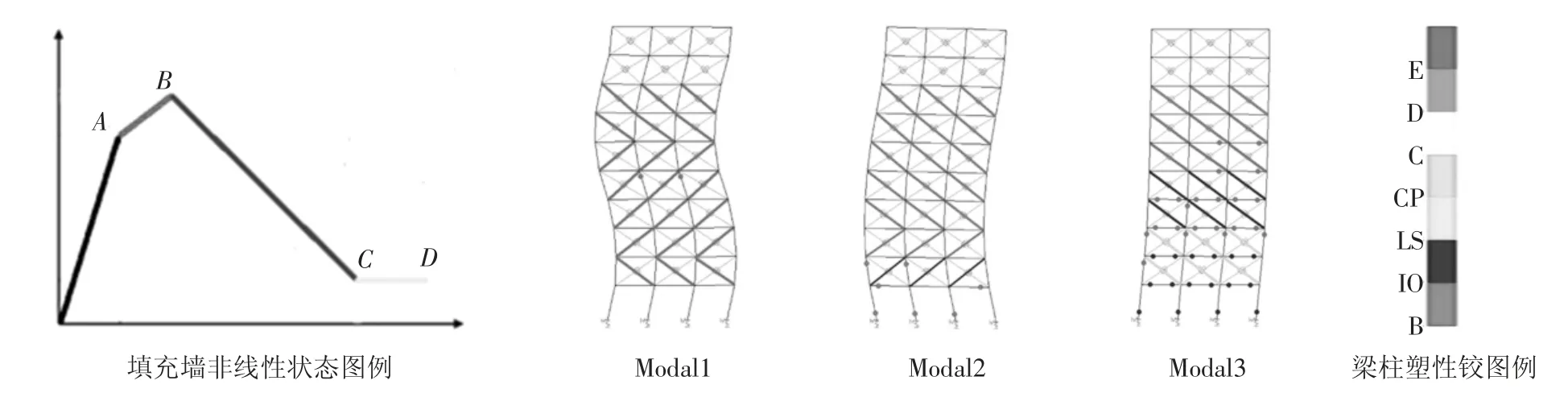
图16 Ⅲ类场地结构前三阶模态梁柱塑性铰分布及填充墙非线性发展Fig.16 Distribution of plastic hinges and nonlinear development of filled wall in the first three-order modal of structures on site Ⅲ

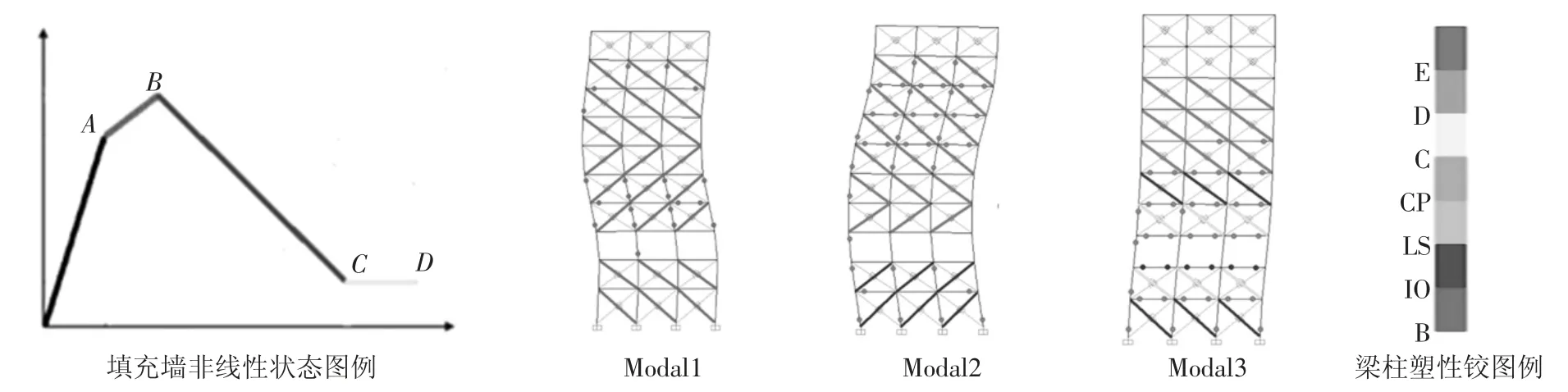
图17 刚性地基前三阶模态梁柱塑性铰分布及填充墙非线性发展Fig.17 Distribution of plastic hinges and nonlinear development of filled wall in the first three-order modal of structures on rigid foundation