结构动力时程分析的地震动选择方法研究

张耀庭，刘勇，沈杰，邹志文，余昕叶

（华中科技大学土木工程与力学学院，湖北武汉 430074）

随着计算机以及有限元技术的不断发展，结构抗震性能研究广泛地采用动力时程分析方法，同时《建筑抗震设计规范》（GB 50011—2010）[1]规定某些特定建筑需要采用时程分析法进行多遇地震下的补充计算，而合理的地震动输入是保证计算结果相对准确的前提.地震动本身就具有极强的随机性，不同的地震动计算结果差距可能高达数倍，而大部分研究者或工程人员采用的是标准化的实际地震动，并未考虑场地和结构特性，从而导致结构响应存在较大的离散性和不合理性[2].

从20 世纪80 年代起，国内外众多学者对地震动进行了大量的研究，并提出了一些地震动选择方法.Nau[3]等提出了基于地震反应谱的缩放选波方法，这种方法的思路后来也被广泛接受，很多西方规范中推荐的方法均受其影响.Naeim[4]等利用遗传优化算法进行地震动的选择，使其反应谱中值与设计反应谱相匹配.Nirmal 等[5]利用蒙特卡洛法和贪婪算法提出了一种更有效的地震动的选择方法，选出的地震动记录的反应谱均值与设计反应谱高度匹配，离散性也较小.Haydar[6]等提出了用和声搜索法进行基于欧洲规范下的地震动选择，结果表明所选地震动的平均反应谱与规范目标谱有较好匹配.《建筑抗震设计规范》（GB 50011—2010）[1]要求在结构的主要周期点处所选地震动反应谱与规范设计反应谱统计意义上相符（简称周期点法），但规范过于笼统，使其可操作性较差.王亚勇[7-8]等提出了一种基于反应谱形状特征的选择地震动的方法，并以规范中加速度设计反应谱为标准，按近场地震、远场地震和反应谱特征周期分类的方法对地震动进行分组.杨溥[9]等提出基于规范设计反应谱平台段和结构基本自振周期段的两频率段控制的选波方案（简称双频段法），依据所选地震动的反应谱与设计反应谱一致的原则，对比分析得出该方法的合理性.高炳鹏[10]等提出对场地特征周期及结构基本周期附近反应谱与规范设计反应谱的面积进行拟合（简称面积法），并与周期点法进行对比分析得出各方法适用性.综上所述，地震动选择的基本思路均是让所选择地震动的反应谱与相应的设计反应谱相一致，但在所选地震动反应谱与设计反应谱的匹配程度上尚存有争议.

为此，本文根据我国现规范设计了两榀不同周期的PC 框架结构，利用Matlab 分别得到周期点法、双频段法、面积法以及改进的和声搜索法最优的7条地震动.在OpenSees 中进行动力时程分析，并对比其结果的准确性和离散性，以期为结构抗震分析时，合理地确定地震动的选择方法提供参考依据.

1 地震动备选数据库

随着地震动记录不断地收集，全世界的实际地震动数据库也在不断的扩大，本文从美国太平洋地震工程研究中心（PEER）的NGA-West2 中选择了一组含有766 条水平强地震动的地震动集作为地震动备选数据库，在本文研究中，对每个地震动仅考虑两条水平分量的加速度记录.地震动备选数据库的选择标准如下[11-12]：

1）地震动震级：所选地震动震级为6.0 ～8.0；

2）断层距：场地的断层距为0 ～60 km；

3）场地类型：场地类型为C 类，剪切波速为260 m/s ≤Vs30≤510 m/s，对应国内的Ⅱ类场地；

4）地面峰值加速度：PGA ＞ 0.05 g，保证备选地震动有一定的强度；

5）有效持时：需满足D5-95≥15 s.

根据上述标准在PEER 中选出了766 条满足要求的地震动记录，其加速度反应谱如图1 所示.

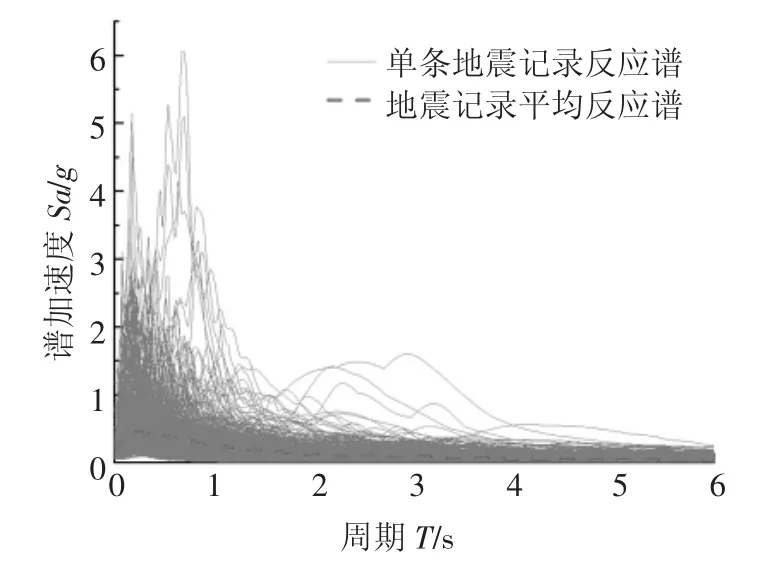
图1 备选766 条地震动加速度反应谱（ξ=3%）Fig.1 Alternative 766 earthquake acceleration response spectrums（ξ=3%）

2 地震动选择方法

地震动选择的基本原则是要求所选地震动的加速度反应谱与设计反应谱相一致，但实际地震动加速度反应谱不可能与设计反应谱在全周期都有很好的匹配，所以在匹配的周期段和方法上都具有较大的可研究性.以下是对4 种地震动选择方法（记为A、B、C、D）进行的对比分析.

2.1 周期点法（方法A）

《建筑抗震设计规范》（GB 50011—2010）[1]规定了时程分析法中多遇地震和罕遇地震下的弹性和弹塑性验算的方法，且在建筑抗震计算时某些建筑还需采用时程分析法进行多遇地震下的补充计算.当取7 条及7 条以上的时程曲线时，计算结果取时程法的平均值和振型分解反应谱法的较大值.对于地震动的选择方法，其中也规定了在采用时程分析法时，多条时程曲线的平均地震影响系数曲线应与设计反应谱在统计意义上相符.虽然规范对选波方法提出了一定的要求，但具体的实施过程并没有详细的规定，从而导致操作人员在选波过程中也存在着差异，该方法的研究步骤主要分为3 步：

1）根据场地建筑的抗震设防烈度和地震烈度水准在规范中得到相应的加速度时程的最大值，并把备选的766 条地震动的加速度最大值统一线性调幅到相应的值.

2）利用Matlab 软件编写选波程序，得到7 条与设计反应谱在统计意义上相符的地震动.即每条地震动的加速度反应谱与设计反应谱相比，在结构的前三周期（主要振型周期）相差都不大于20%，这样保证了所选地震动在进行时程分析时与振型分解反应谱法计算结果的一致性.再根据三个主要振型周期上反应谱的差值的均方根误差（RMSE）从小到大依次选择出7 条合理的地震动.

3）规范中对时程分析的计算结果也进行了相关的规定：在进行弹性时程分析时，每条时程曲线计算所得的结构底部剪力不应小于振型分解法计算的65%；多条时程曲线计算所得结构底部剪力的平均值不应小于振型分解反应谱法计算结果的80%，如均满足即为本方法最合理的地震动选择.

2.2 双频段法（方法B）

双频段法主要是在杨溥[9]等人的研究基础上进行了一定的改进，得出了更有效的关于双频段的地震动选择方法.该方法对反应谱进行了两个频段的控制：分别是对规范设计反应谱中的[0.1，Tg]平台段和结构基本周期T1附近[T1-0.2，T1+0.5]段进行控制，要求每条所选地震动的加速度反应谱在这两段的值与设计反应谱分别相差不超过10%.该方法的研究步骤主要分为两步：其一同周期点法中的步骤1；其二是利用Matlab 软件编写选波程序，得到在双频段上分别满足要求的地震动，并根据双频段上反应谱差值的RMSE 从小到大依次选择出7 条合理的地震动.

2.3 面积法（方法C）

面积法主要是在高炳鹏[10]等人的论述方法中进行了一定的调整，同时也方便与双频段法的对比，该方法对两个频段的反应谱面积值进行了控制：分别是对规范设计反应谱中的[0.1，Tg]平台段和结构基本周期T1附近[T1-0.2，T1+0.5]段进行控制，要求每条所选地震动的加速度反应谱在这两段的面积值与设计反应谱中的面积值分别相差不超过10%，该方法的具体研究步骤与双频段法类似.

2.4 改进的和声搜索法（方法D）

和声搜索算法[13]是一种启发式全局搜索算法，该方法的最初灵感来源于音乐演奏中乐师们凭借自己的记忆，通过反复调整乐队中各乐器的音调，最终达到一个美妙和声状态过程的模拟.HS 算法将乐器i（i=1，2，…，m，此处为所有备选地震动编号）类比于优化问题中的第i 个设计变量，各乐器声调的和声 Hj（j=1，2，…，HMS，此处为地震动集的组号）相当于优化问题的第j 个解向量，评价标准类比于问题公式化后的目标函数.算法首先产生HMS（和声记忆库大小）个初始解放入和声记忆库HM 内，以概率HMCR（和声记忆库取值概率）在HM 内搜索新解，以概率1-HMCR 在HM 外变量可能值域中搜索.然后算法以概率PAR（音调微调概率）对新解在±BW（音调微调带宽）范围内进行局部扰动.若新解的目标函数值优于HM 内的最差解，则替换之；否则保持HM 不变，然后不断迭代，直至达到预定迭代次数Tmax为止，最终得到最优的和声解向量（此处为最优的地震动集）.Geem[14]等提出了和声搜索优化算法后，该方法大量的应用于各种优化组合的问题，同时较遗传算法、模拟退火算法和禁忌搜索等算法有更好的计算效率和精确度.

一组地震动的选择也是一种优化组合的问题，所以也适用于地震动的选取.Haydar[6]等提出了用和声搜索法进行基于欧洲规范下的地震动选择，针对不同场地类别以及控制参数分别选出7 条地震动记录，结果表明所选地震动的平均反应谱与规范目标谱比较接近，能很好的满足规范要求.黄丹[12]提出了基于优化级排序的改进后的和声搜索法，并得到了适用于我国规范的地震动记录，通过选出的50 组地震动进行结构的动力时程分析，验证了该方法的适用性和稳定性.虽然上述和声搜索方法都能选择出平均反应谱与规范设计反应谱较匹配的地震动记录，但由于在定义约束条件时，没有对单条地震动进行约束，以及进行地震动选择时，没有考虑结构本身的特征，从而导致选出单条地震动的反应谱与设计反应谱差异较大，且作用于结构进行动力时程分析时结构响应的离散性也较大.

由于约束条件不同，其地震动选择结果也会有较大的差异，本文对其约束条件进行一定的改进.为了考虑结构本身的特征，在选择地震动时，要求所选单条地震动的结构基本周期处反应谱值与设计反应谱值在统计意义上相符，在约束条件中添加一个与结构基本周期相关的约束，最终得到一组使结构响应离散性较小的地震动记录.该方法主要分为以下步骤，其算法程序见图2.

1）同周期点法的步骤1；

2）Matlab 编程处理，问题公式化并得到目标函数f（x）的表达式；

式中：e 所选地震动反应谱均值与设计反应谱值在特定周期内差值的均方根误差，其取值如下式：

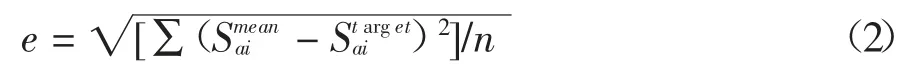
g1—约束条件1，控制所选地震动反应谱均值与设计反应谱在特定周期内每点的差值在10%以内，其取值如下式：

g2—约束条件2，确保每组地震动不能出现相同的地震动，其取值如下式：

g3—约束条件3，控制每条所选地震动在结构基本周期处其加速度反应谱值与设计反应谱值在20%以内，其取值如下式：

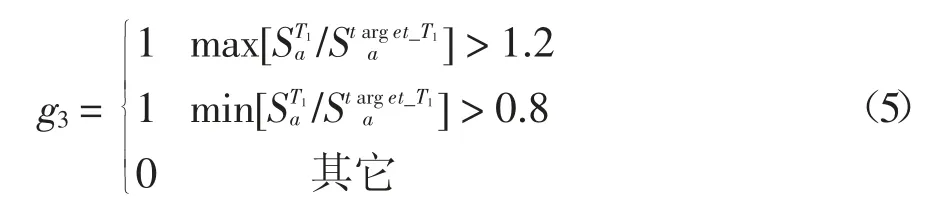
3）确定控制参数：Geem[15]等研究结果推荐HMCR 在 0.7 到 0.95 之间，PAR 在 0.2 到 0.5 之间以及HMS 在 10 到 50 之间.Degertekin[16]推荐 HMCR 取 0.8，PAR 取 0.4 以及 HMS 取值在 50 到 100 之间.本研究中，HMCR 为 0.8、PAR 为 0.4、HMS 为 50、BW 与地震动备选数据库大小相关并取值为20、最大迭代次数（Tmax）为 1 000 000 和匹配周期段为[0.5T1，2T1].

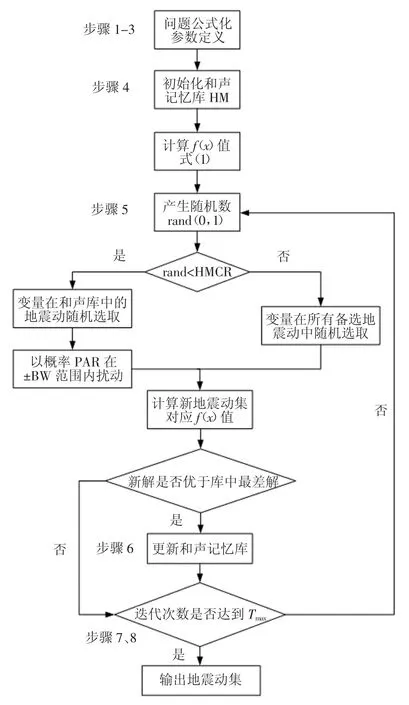
图2 改进的和声搜索法程序Fig.2 The program of improved harmony search method

4）初始化和声记忆库（HM）：在地震动备选数据库中随机选择HMS 组地震动，通过式（1）计算每组地震动的f（x）值；

5）即兴生成新的和谐解向量：通过和声记忆库取值概率（HMCR）、音调微调概率（PAR）、音调微调带宽（BW）进行即兴创作，生成一个新的和谐解向量；

6）更新和声记忆库（HM）：当即兴生成的和谐解向量的f（x）值小于和声记忆库中f（x）的最大值时，则用该和谐解向量取代f（x）最大值的向量；否则，保持原来的和声记忆库不变.

7）重复步骤5、6，直至达到最大迭代次数.

8）最终得到50 组分别含有7 条地震动的集合，并选出f（x）值最小的地震动集.

3 地震动选取算例及分析

3.1 结构分析模型

本文按照《建筑抗震设计规范》（GB 50011—2010）[1]、《混凝土结构设计规范》（GB 50010—2010）[17]和《预应力混凝土结构抗震设计规程》（JGJ 140—2004）[18]设计了两榀 PC 框架结构，层数分别为 3 层（YKJ01）和 8 层（YKJ02），框架的抗震等级分别为二级和一级.抗震设防烈度为8 度，设计基本加速度值为0.2 g，场地类别为Ⅱ类场地，设计地震分组为第一组，场地特征周期为0.35 s，结构阻尼比为0.03.女儿墙等效线荷载为2.5 kN/m，填充墙等效线荷载为10 kN/m，结构荷载信息见表1，框架结构立面和平面信息分别见图3 和图4，并选取C 轴框架进行结构分析.

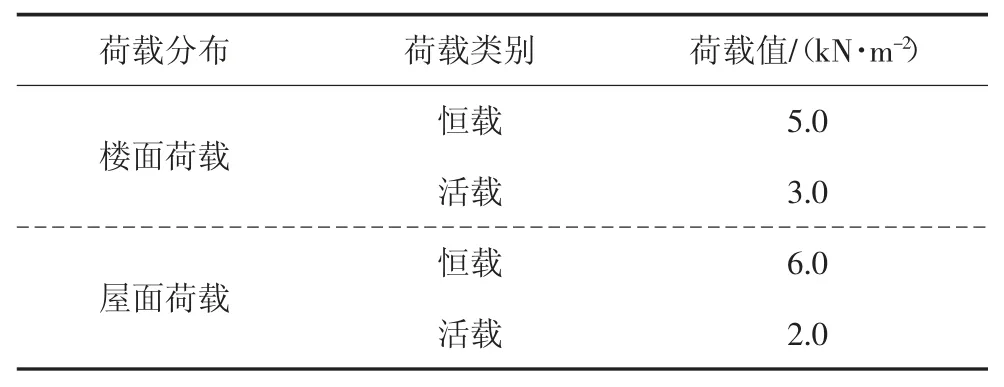
表1 结构荷载信息Tab.1 Structural load information

图3 框架结构立面图Fig.3 Elevation of frame structures

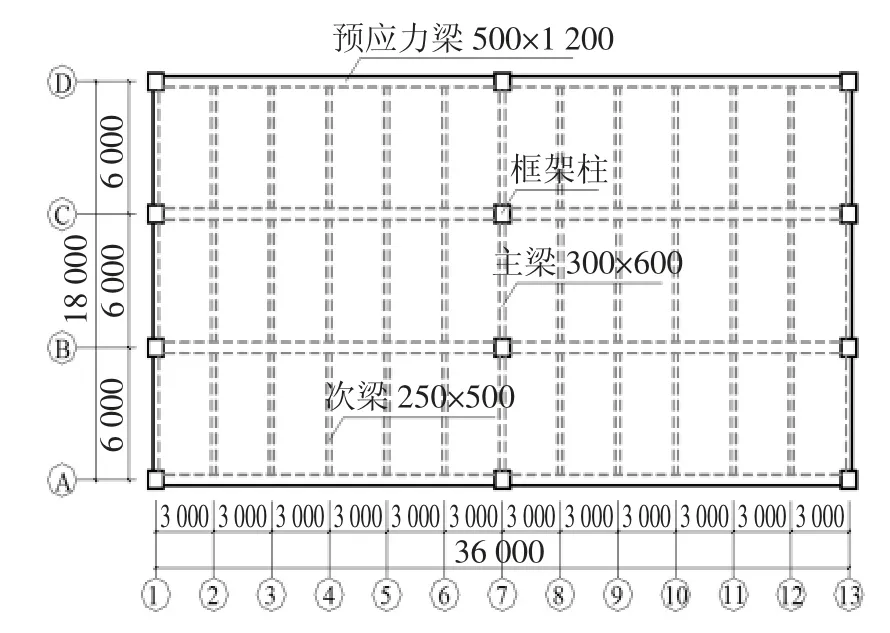
图4 框架结构平面图Fig.4 Plane of frame structures

屋面和楼面板厚120 mm，混凝土强度等级为C30，梁、柱混凝土强度等级为C45，预应力筋采用极限抗拉强度标准值ftpt为1 860 MPa 的φs15.2 低松弛钢绞线，纵筋和箍筋均采用HRB400 级钢筋，配筋信息见表2，其前三阶结构周期见表3.

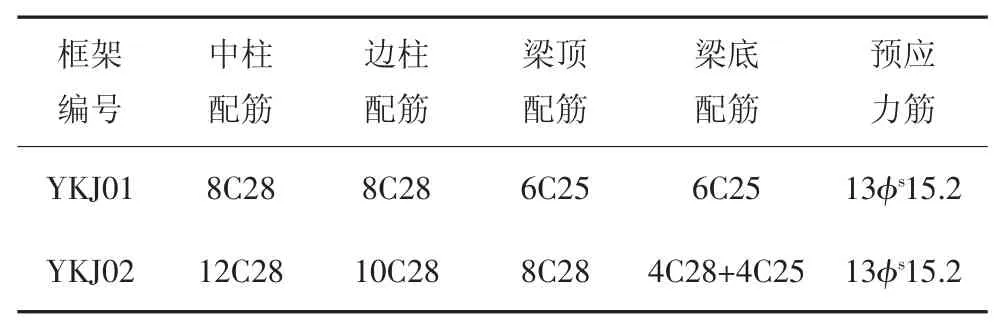
表2 梁柱配筋信息Tab.2 Reinforcement information of beam and column

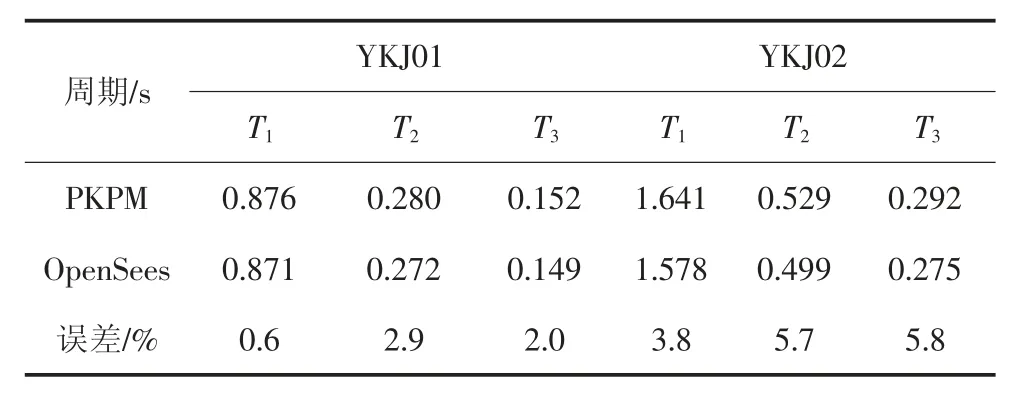
表3 PC 框架前三阶周期Tab.3 The first three period of the PC frame

本文用OpenSees 进行建模分析，混凝土本构采用Concrete02 模型，考虑了混凝土的受拉性能和箍筋的约束效应；普通钢筋本构采用Steel02 模型，考虑了钢筋等向应变硬化影响和包辛格效应；预应力筋本构采用Hysteretic 模型，考虑了其滞回捏拢效应和卸载刚度退化，并通过Initial Strain Material 模型给预应力筋初始应变以施加预应力[19-21].

考虑楼板对梁刚度的影响，预应力梁采用T 型截面，两侧翼缘宽度均取6 倍板厚，梁、柱混凝土截面分为核心区和保护区，见图5.框架的普通钢筋混凝土部分采用非线性梁柱单元，PC 梁由普通钢筋混凝土单元、预应力筋和刚臂单元组成.每根PC 梁划分为12 个单元，每根柱划分为4 个单元，每个单元均包含4 个Gauss-Lobatto 积分点.

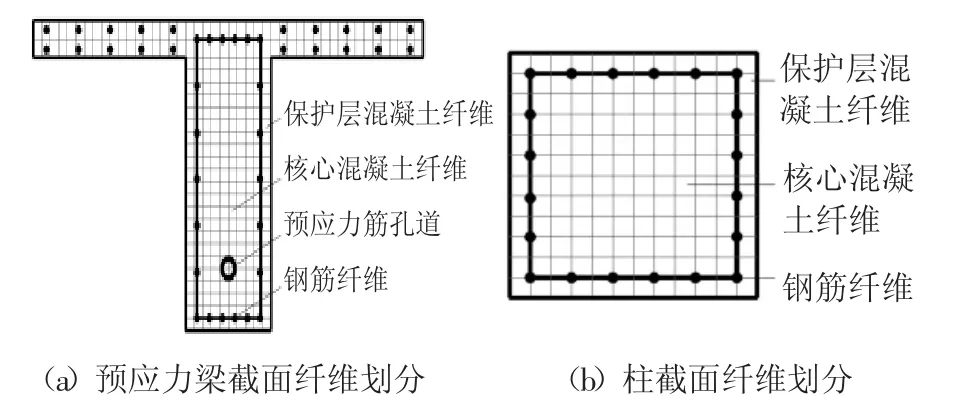
图5 框架梁、柱截面纤维划分Fig.5 Section mesh for beam and column fiber models

3.2 地震动选择

利用上述4 种地震动选择方法，对各条备选地震动加速度反应谱进行不同条件下与目标谱的匹配，分别在766 条地震动备选数据库中选出合适的7条地震动，各个方法选取的地震动记录见表4 和表5，其地震动加速度反应谱见图6～9，且得到的地震动加速度反应谱与规范设计反应谱的统计特性在各自匹配段均具有较好的一致性.

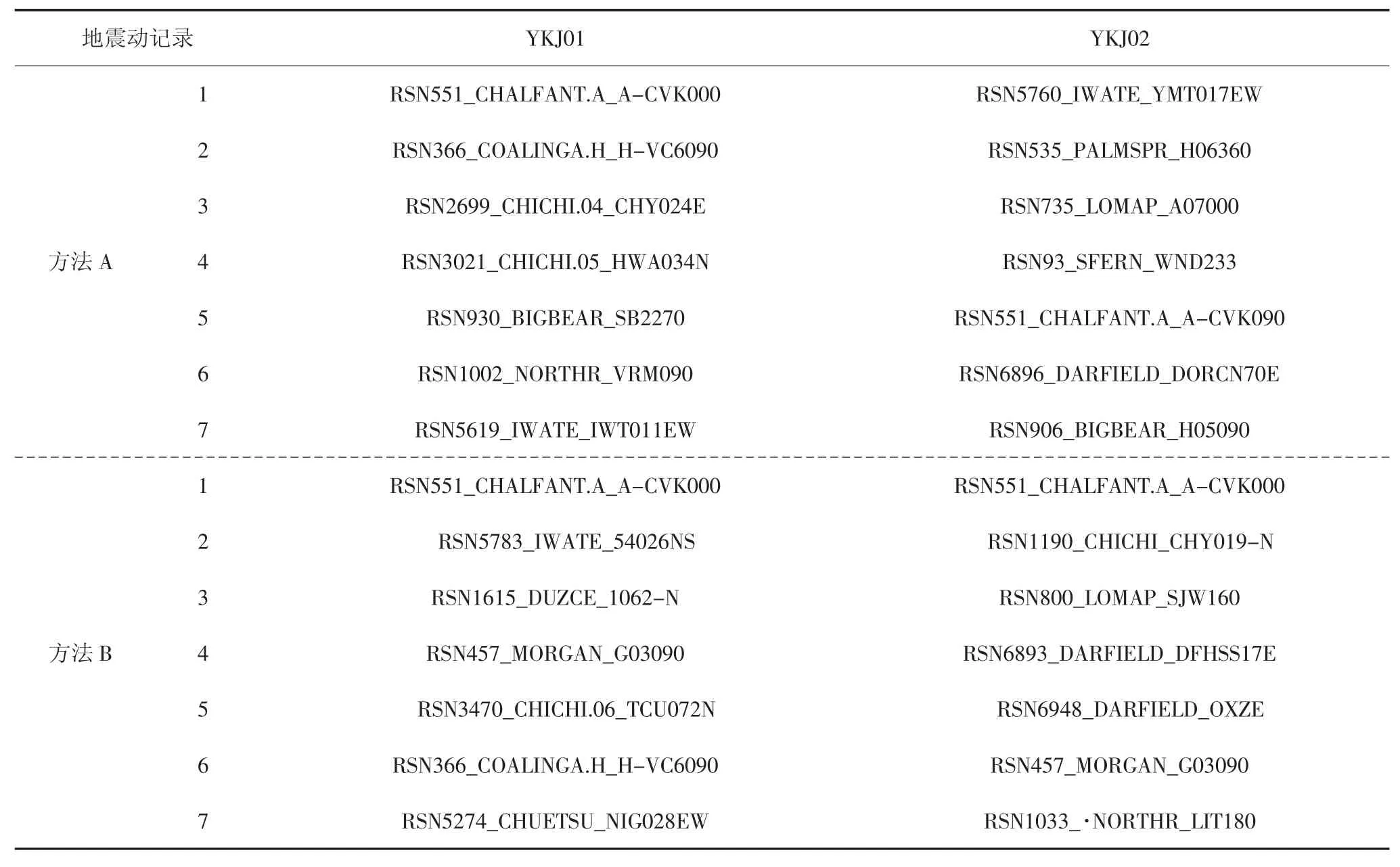
表4 方法A 和方法B 选取的地震动记录Tab.4 Selection of ground motion records for method A and B

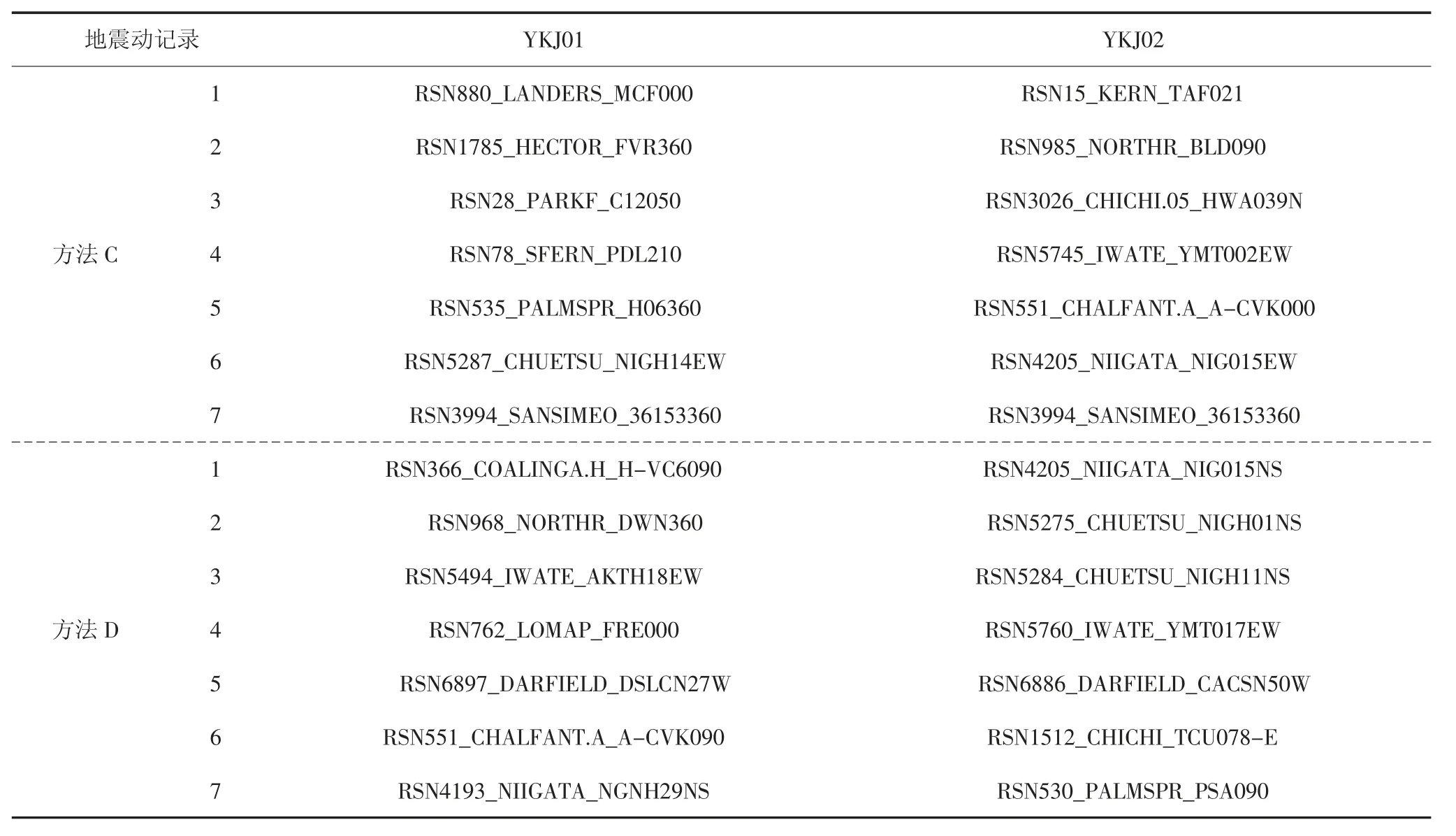
表5 方法C 和方法D 选取的地震动记录Tab.5 Selection of ground motion records for method C and D

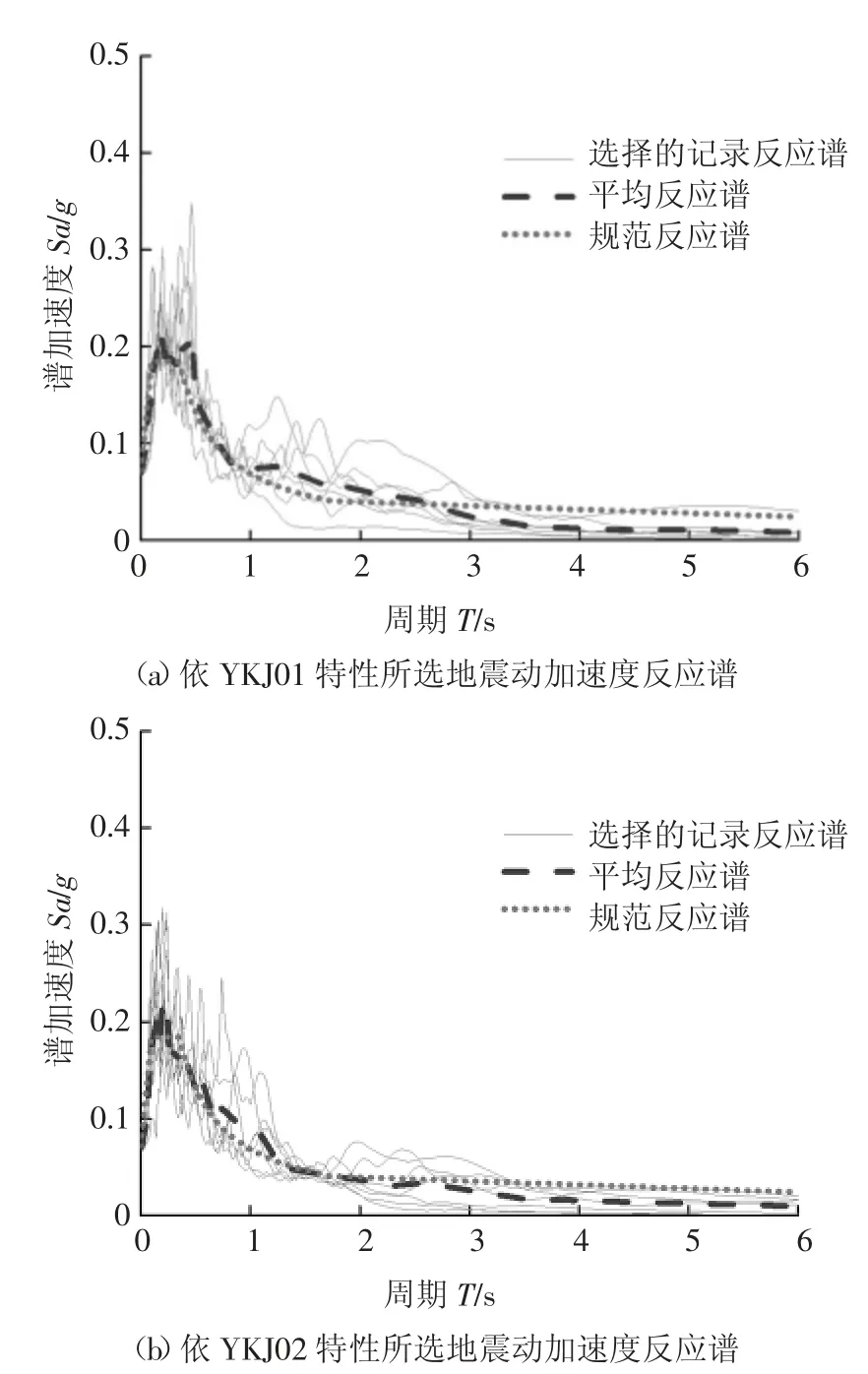
图6 方法A 地震动选择结果Fig.6 Result of ground motion selection for method A

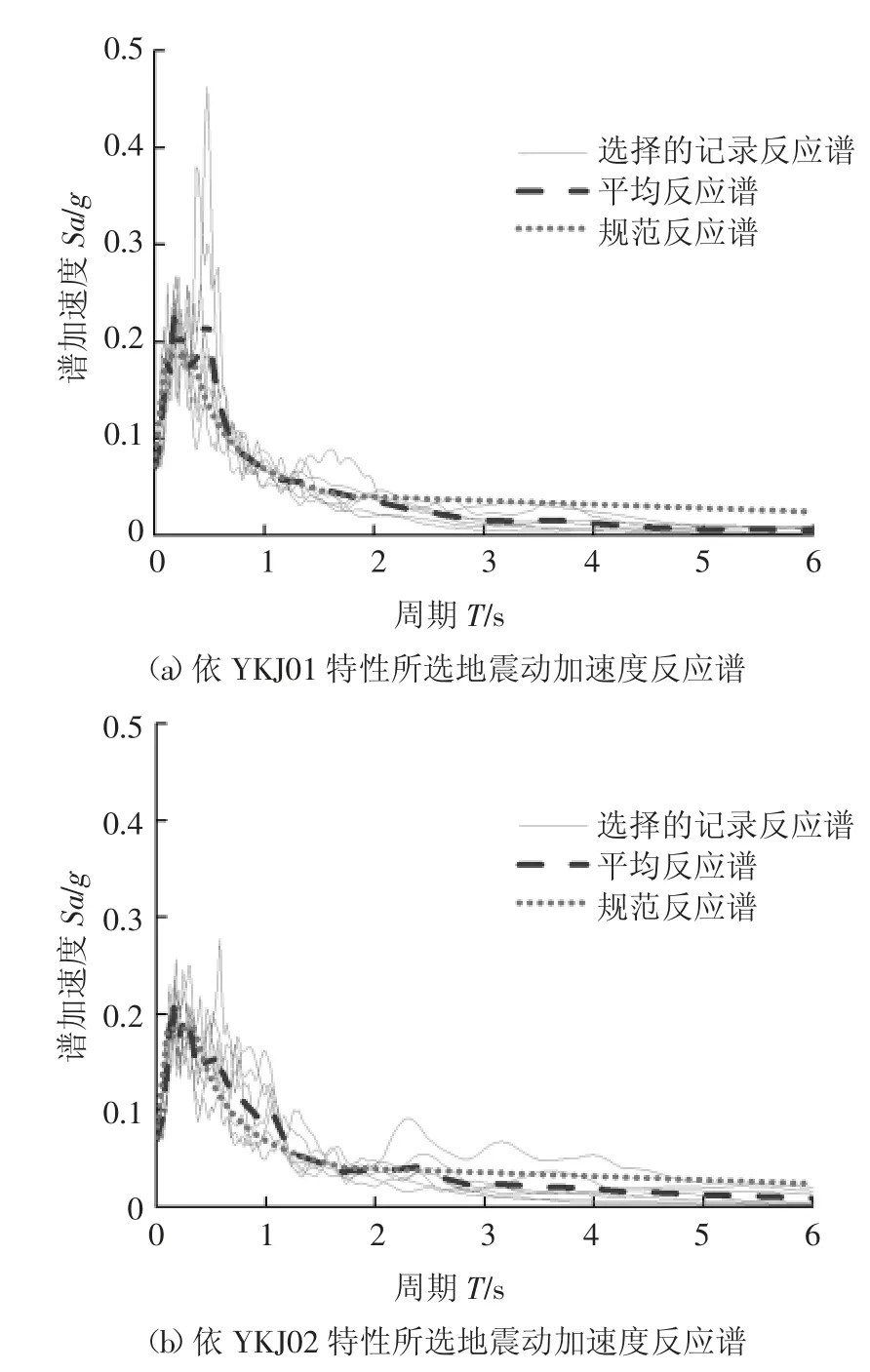
图7 方法B 地震动选择结果Fig.7 Result of ground motion selection for method B

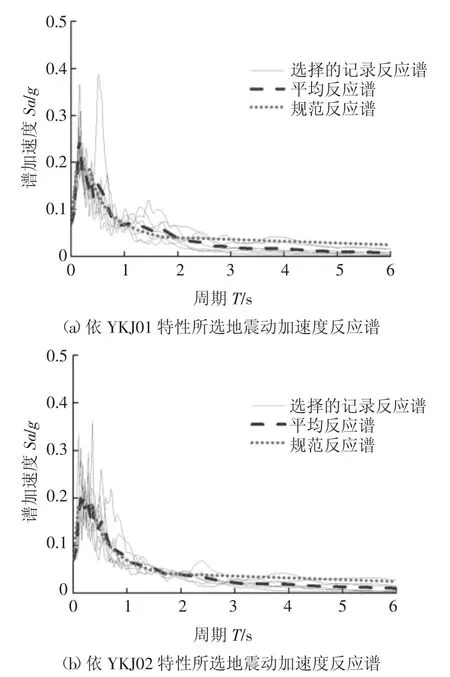
图8 方法C 地震动选择结果Fig.8 Result of ground motion selection for method C

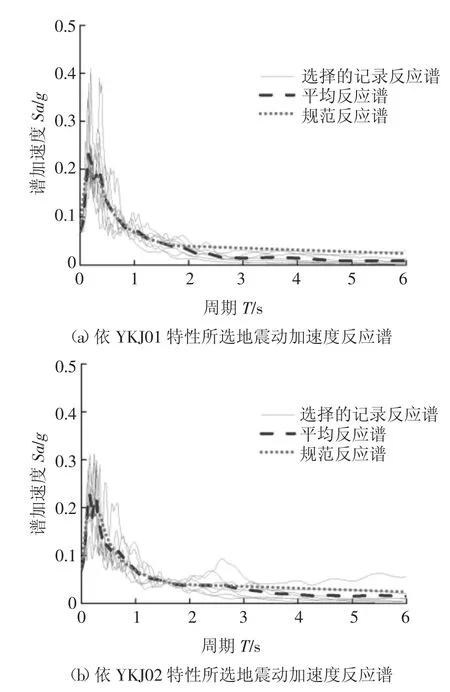
图9 方法D 地震动选择结果Fig.9 Result of ground motion selection for method D

3.3 结构动力时程分析结果对比分析

本文利用上述4 种方法得到的地震动进行动力时程分析输入，分别计算结构在多遇地震和罕遇地震作用下的响应，包括底部剪力、顶点位移和最大层间位移角，分析结果见表6 和表7.其中多遇地震下加速度峰值取为70 cm/s2，罕遇地震下加速度峰值取为400 cm/s2.

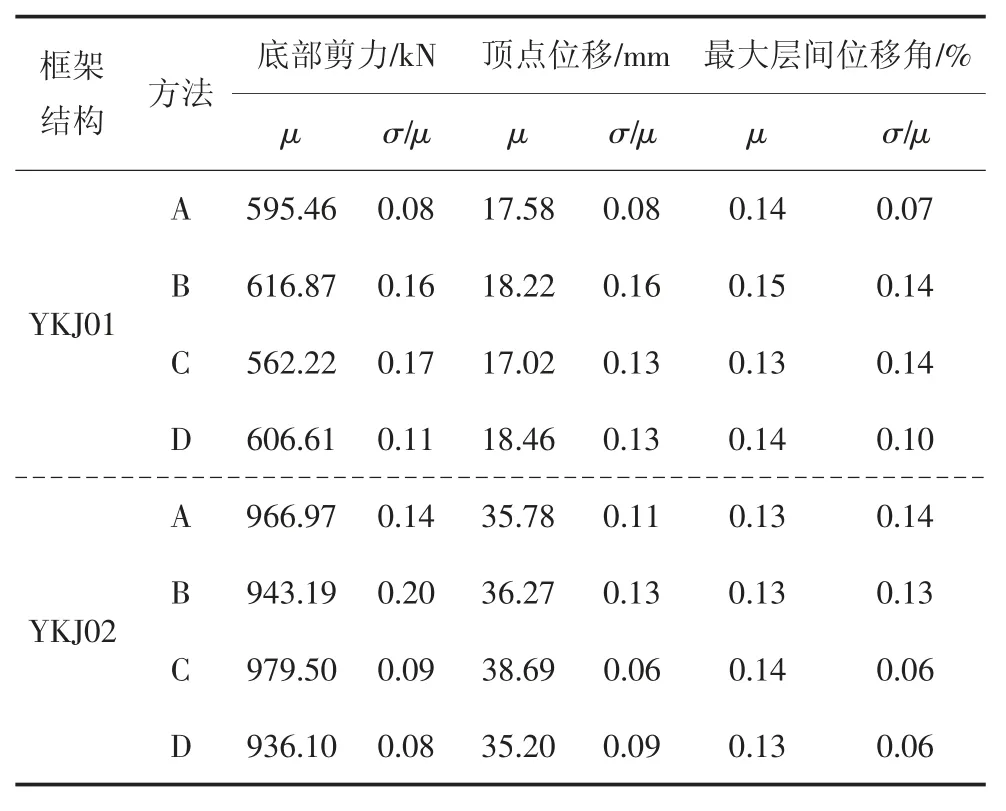
表6 多遇地震作用下结构动力响应Tab.6 Structural dynamic response under frequently earthquake

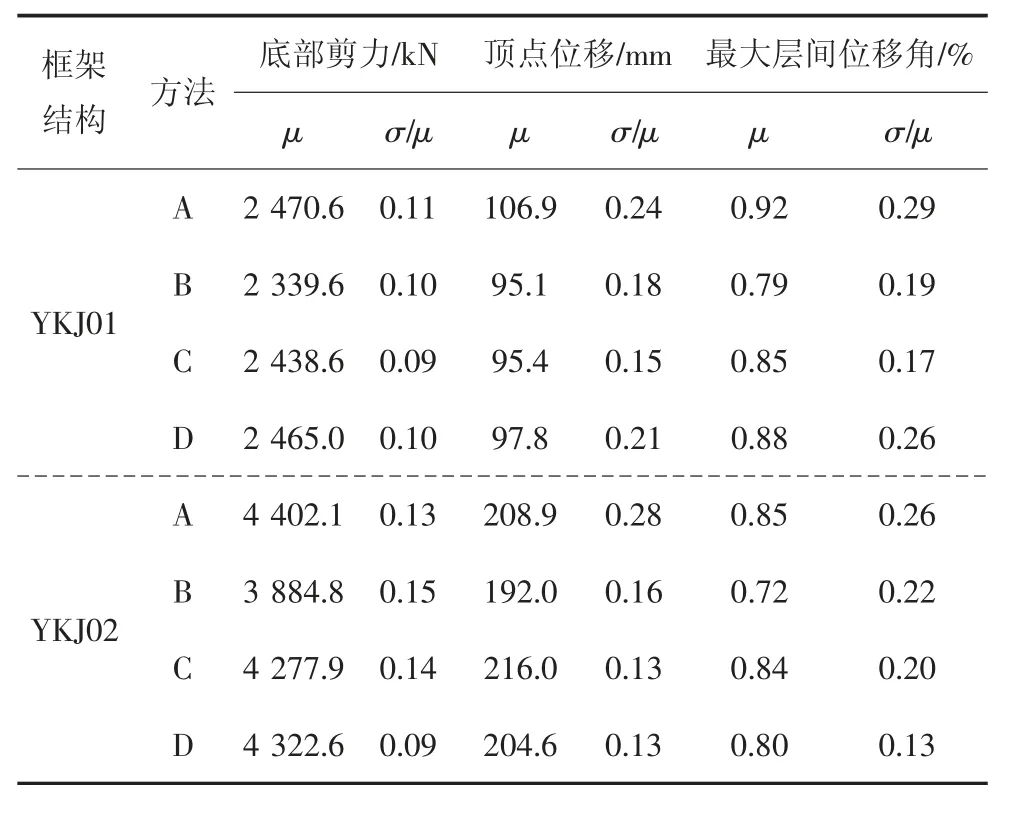
表7 罕遇地震作用下结构动力响应Tab.7 Structural dynamic response under rarely earthquake

由表6 多遇地震作用下结构的动力响应可以看出方法A 和方法D 得到的结果，包括底部剪力、顶点位移和最大层间位移角离散性均较小.方法A 和方法D 的结构响应参数指标的变异系数在10%左右，而方法B 的结构响应参数指标的变异系数在15%左右，方法C 的YKJ01 和YKJ02 结构响应参数指标的变异系数分别在15%和10%左右.

由表7 罕遇地震作用下结构动力响应可以看出方法C 和方法D 得到的结果离散性较小.方法C 和方法D 的结构响应参数指标的变异系数在15%左右，而方法A 和方法B 的结构响应参数指标的变异系数在20%左右，且结构已进入弹塑性阶段，构件刚度退化导致结构基本周期变长，所以方法A 不适用于弹塑性时程分析的地震动选择过程.

由表6 多遇地震和表7 罕遇地震作用下各种方法计算结果响应参数平均值之间的差值均在10%左右，表明4 种地震动选择方法计算结果的结构响应具有较好的准确性和一致性.

根据《建筑抗震设计规范》（GB 50011—2010）[1]：弹性时程分析时，多条时程曲线计算所得结构底部剪力的平均值不应小于振型分解反应谱法计算结果的80%.由结构弹性底部剪力对比结果（见表8 和图10）可以看出4 种选波方法都能很好的满足规范要求，其中依照方法B 和方法D 选波的结构弹性底部剪力计算结果与振型分解反应谱法对底部剪力的计算结果更加接近，误差值均在2%左右，更加符合设计水准.

最大层间位移角作为结构弹塑性分析响应的重要参数，在罕遇地震作用下要求钢筋混凝土框架层间位移角限值为1/50.本文4 种方法选出的地震动对结构进行弹塑性动力时程分析，其结果见图11.对于YKJ01 和YKJ02 结构，目标反应的最薄弱楼层分别出现在第1 和第2 层，最大层间位移角的平均值分别约为1/110 和1/125，均满足最大层间位移角的限值要求.

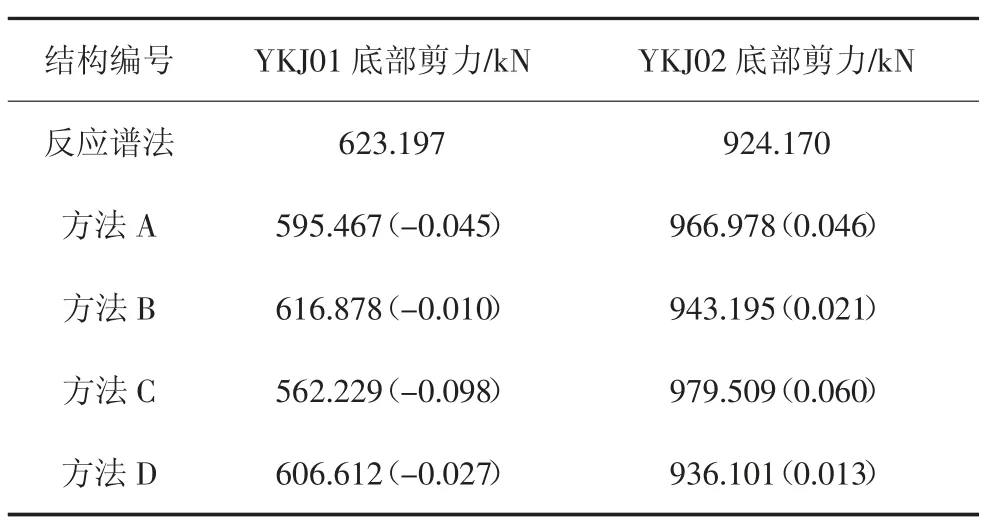
表8 结构弹性底部剪力对比Tab.8 Base shear force comparison with structural elastic

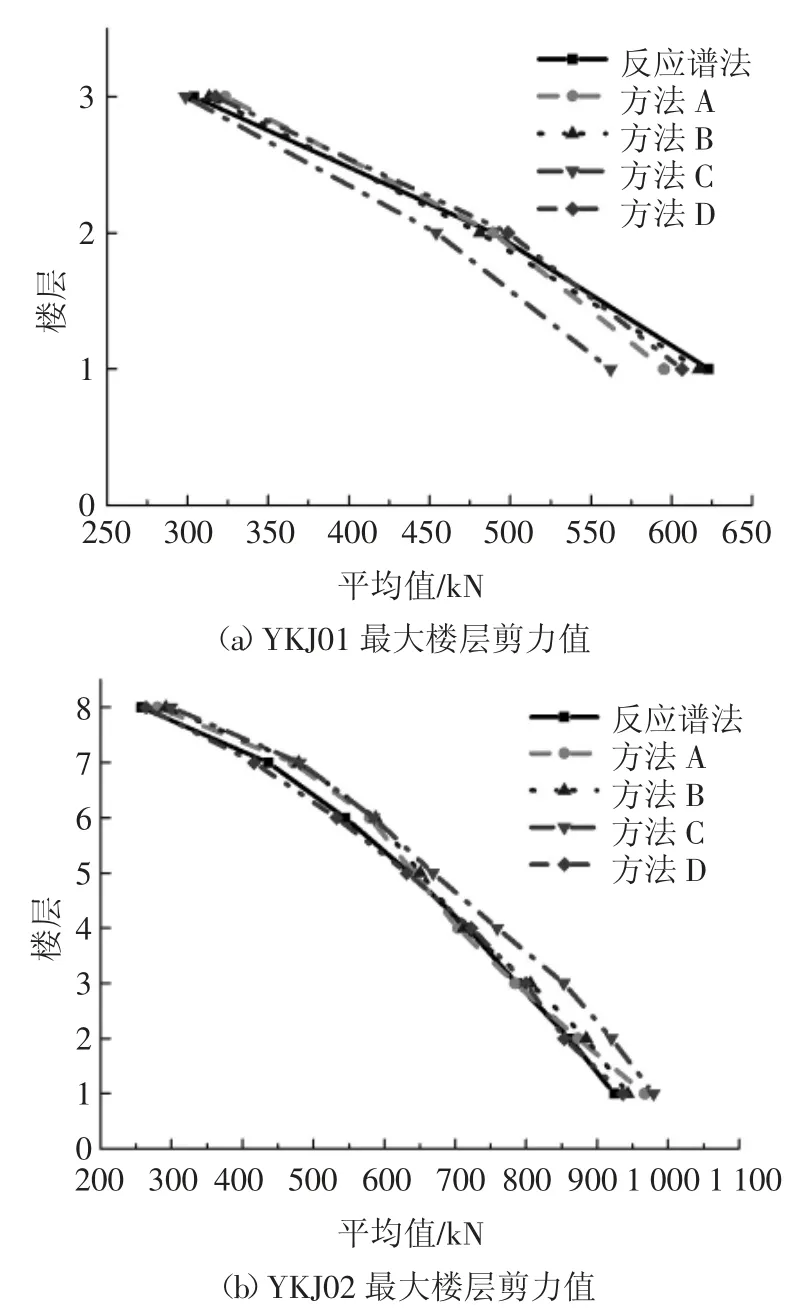
图10 结构弹性最大楼层剪力值Fig.10 Maximum floor shear value of elastic structure

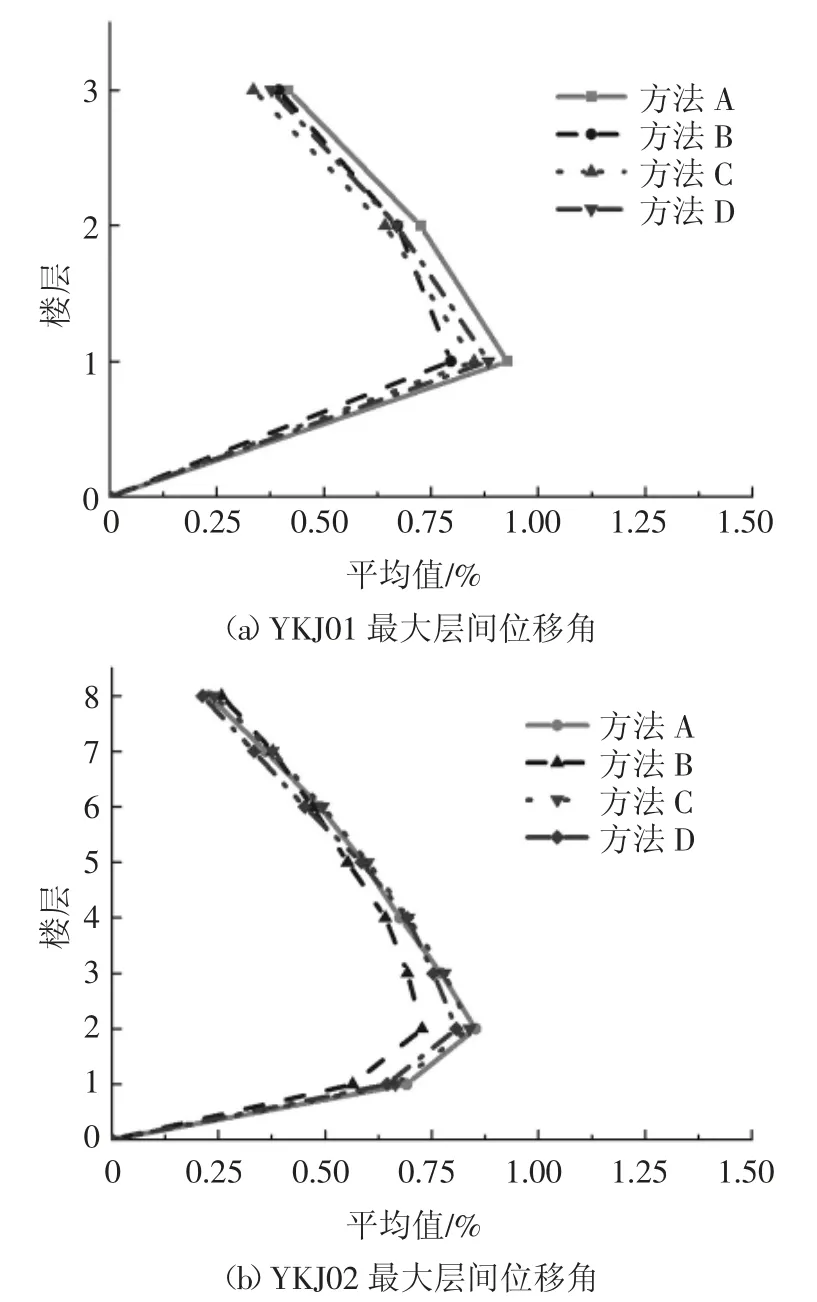
图11 结构弹塑性最大层间位移角Fig.11 Maximum inter-story drift ratio of elastoplastic structure

4 结 论

本文通过改进现有的和声搜索法进行地震动的选取，针对依据我国现规范设计的两榀不同周期的PC 框架结构在OpenSees 中进行了动力时程分析，并与其他3 种常用的选波方法的计算结果进行对比，所得到的主要结论如下：

1）多遇地震作用下，周期点法和改进的和声搜索法的结构响应参数的离散性更小，其变异系数在10%左右；通过底部剪力的对比，双频段法和改进的和声搜索法得到的计算结果与振型分解反应谱法的结果更接近，误差值均在2%左右，更符合规范设计水准.

2）罕遇地震作用下，面积法和改进的和声搜索法的结构响应参数的离散性更小，其变异系数在15%左右；且周期点法计算结果离散性最大，结构响应参数在25%左右，适用性较差.

3）周期点法只适用于弹性时程分析的地震动选择过程；双频段法没有较严格的控制结构周期点处的反应谱差值，与结构特性匹配程度不足；面积法是对反应谱围成的面积进行匹配，容易出现反应谱明显偏离目标谱的现象；改进的和声搜索法不仅对结构基本周期点处反应谱进行匹配，还对其周期点一定范围内进行较好的匹配，所以该方法无论是对弹性时程分析还是弹塑性时程分析都适用，离散性较小且很好的满足规范的设计水准.因此，本文提出的改进的和声搜索法能更好的满足地震动选择要求.