对称型旅行商问题在工程运输中的应用
2020-07-27胡凯超
胡凯超
(江苏科技大学工程管理系,江苏 镇江 212003)
0 前 言
旅行商问题(Traveling Saleman Problem,TSP)是VRP的特例,由于Gaery已证明TSP问题是NP难题,是指一名推销员要拜访多个地点时,如何找到在拜访每个地TSP问题点一次后再回到起点的最短路径。规则非常容易了解,也贴近人们的生活,但是当要参加的目的地变多时,难度就会急剧增大。本文所列的为30个地方,如果要列举所有路径后再确定最佳行程,那么统计工作量之大,几乎不可能做完。多年来,全球数学家绞尽脑汁,试图找到一个高效的算法,近来在大型计算机的帮助下才取得了一些进展。
“旅行商问题”的应用领域包括:如何规划最合理高效的道路交通,以减少拥堵;如何更好的规划物流,以减少运输成本等[1]。在工程项目中,由于建筑中物资一般会储存在偏远地区以降低成本,故对于物资的运输规划有着非常高的要求,此时对于“旅行商问题”的求解对于提高企业经济效益,加快工程进度具有重要意义。
1 问题的引入
一个工厂将产品运送到各个不同的地点,已知城市个数和各地点之间的路程,要求找到从某一个地点出发,经过所有地点并且每个地点只能被访问一次,最后回到起始点,使总路程最小。以工厂为原点的坐标系,每个运输点的位置相对坐标见表1。
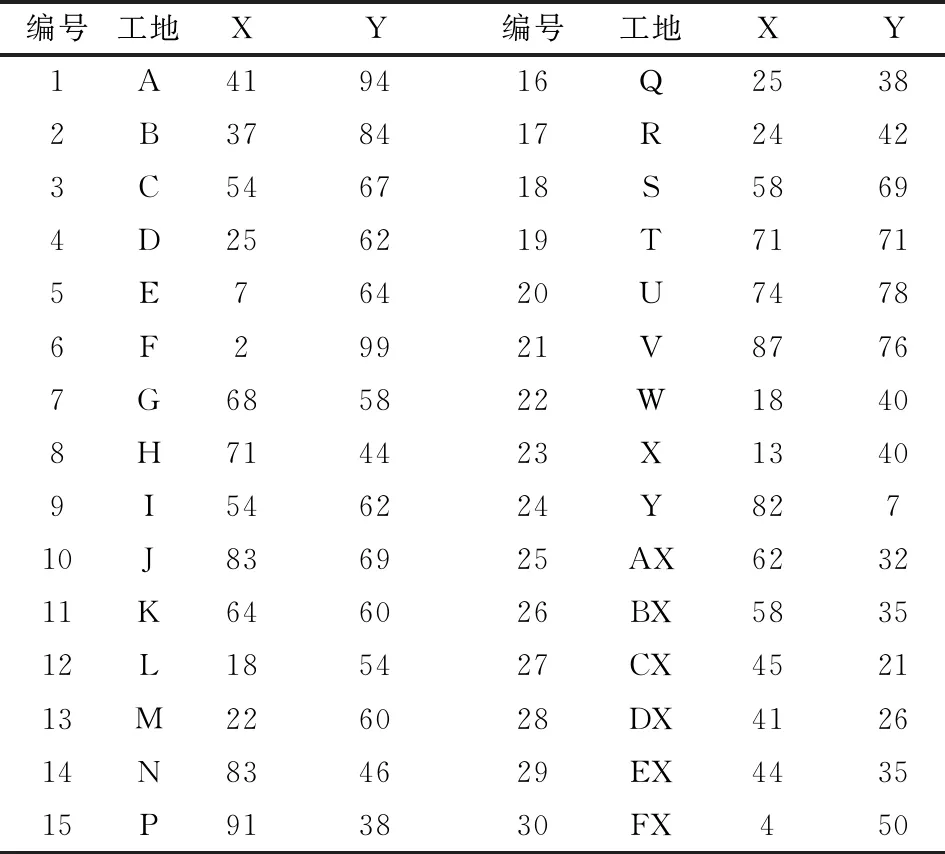
表1 各运输点的位置坐标
因为任意两个工地的往返的距离都是相同的,所以该问题是对称型的,比非对称型的旅行商问题容易一些,不过其最优解的求解过程依然不是一个容易的过程。一般而言,对于旅行地数目较少的TSP问题,可以利用动态规划方法和枚举法手动求出最优解这两种方法显得有些无能为力,通常采用启发式算法式算法借助计算机求其较好的解,比如蚁群算法[2]、基于遗传算法的粒子群算法等。
2 数学模型
蚂蚁k(k=1,2...m)在运动过程中,运动转移的方向由各条路径上的信息量浓度决定。为方便记录可用tabuk(k=1,2...m)来记录第k只蚂蚁当前已走过的所有节点,这里可以称存放节点的表为禁忌表;且该集合会随着蚂蚁的运动状态进行调整。在算法的搜索过程中,蚂蚁会智能地选择下一步所要走的路径。
设m表示蚂蚁的总数量,用dij(i,j=0,1...n-1)表示节点i与节点j之间的距离,τij(t)表示在t刻ij连线上的信息素浓度。在初始时刻,各个位置的信息素浓度是相同的,在t时刻,蚂蚁k从i节点转移到j节点的状态转移概率为:
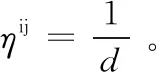
在蚂蚁运动过程中,为了避免在路上残留过多的信息素而使启发信息被淹没,每只蚂蚁在遍历完成后,要对残留信息进行更新处理。由此,在t+n时刻,路径(i,j)上的信息调整如下:
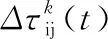
蚁群算法流程见图1。
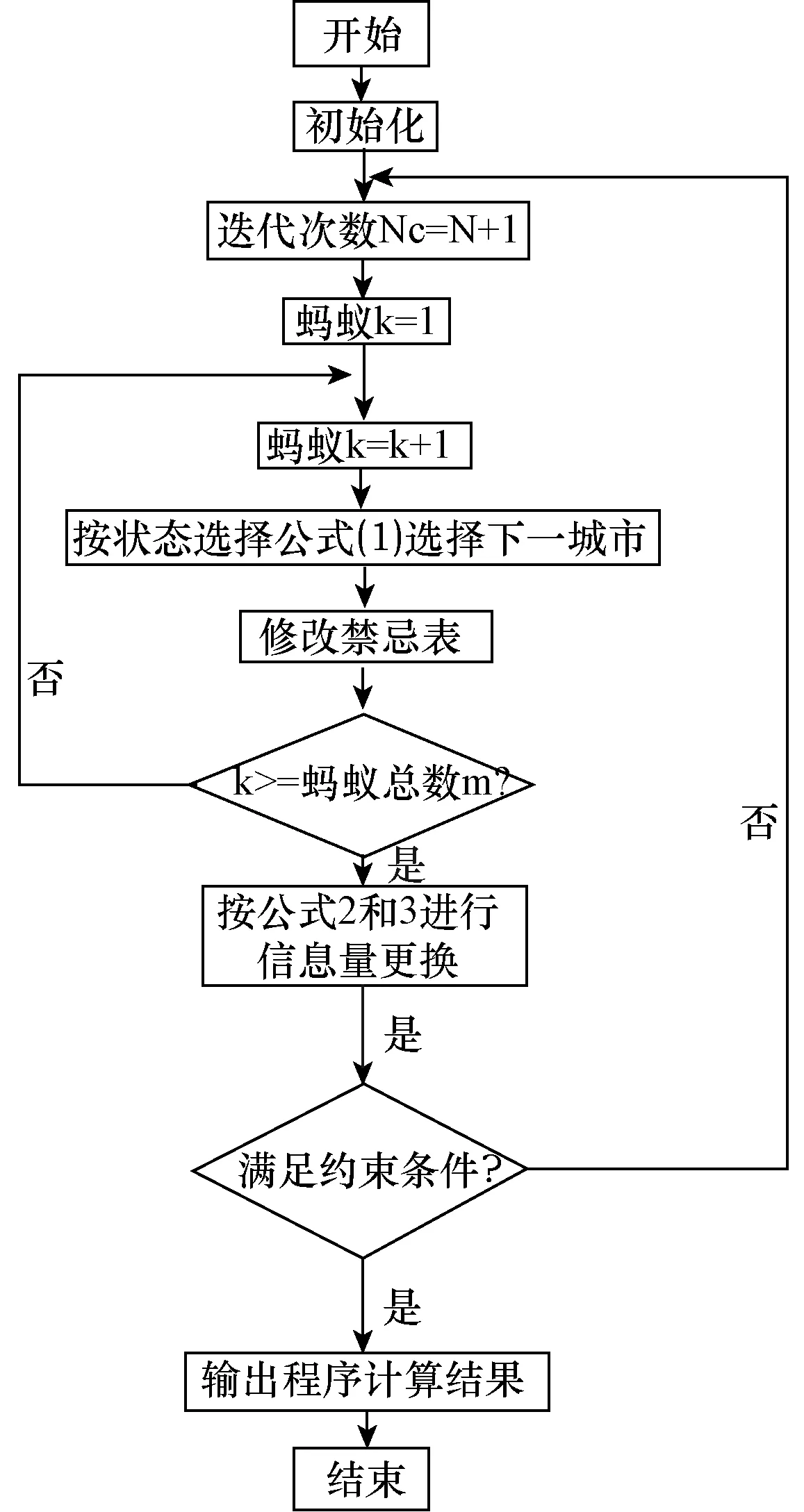
图1 蚁群算法流程
禁忌表:与真实的蚂蚁不同,人工蚁群系统具有记忆功能。为了满足蚂蚁必须经过所有12个不同的工地这一约束条件,为每只蚂蚁都设计了数据结构,成为禁忌表。用来记录t时刻蚂蚁已经经过的工地,不允许该蚂蚁本次循环中在经过改工地,当本次循环结束后,禁忌表被用来计算改蚂蚁所建立的解决方案。之后禁忌表清空蚂蚁又可以自由地选择方案。
运行结果见图2~3。运输的先后顺序见表2。
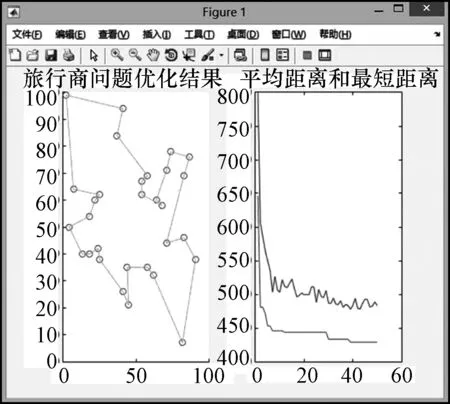
图2 运算结果(1)

图3 运算结果(2)

表2 运输的先后顺序
由此可见,最短路线长为428.959 2。
3 结束语
本文中通过蚁群算法对于工程项目中常遇到的旅行商问题进行了研究,案例中共涉及30个施工场地坐标,虽然是对称型的旅行商问题,但30个点的情况下依然是非常复杂的,案例表明,蚁群算法对于处理此种类型的问题具有求解速度快、答案准确的特点。
[ID:009805]
