Gradient Boosting 算法在典型浅埋煤层液压支架选型中的应用

张 杰，孙 遥，谢党虎，蔡维山，刘清洲，龙晶晶

（1.西安科技大学 能源学院，陕西 西安710054；2.陕西涌鑫矿业有限责任公司，陕西 榆林719407；3.甘肃厂坝有色金属有限责任公司，甘肃 陇南742500）

近年来，大采高综采技术在浅埋煤层开采中得到了广泛应用，已成为煤矿开采主要方向[1]。而由于采高加大，导致采场矿压显现剧烈，极易引发冒顶、压架及片帮等事故，故此，支架阻力的合理选型具有积极意义。目前，支架阻力的选型方法主要有理论计算法、相似模拟法、数值模拟以及神经网络法等。其中理论计算方法[2-4]过于理想化，同实际覆岩有一定差异；数值模拟[5-7]的各项参数同地质条件相关，准确参数难以获取；相似模拟[8-10]对材料要求较高，难以准确模拟实际地质条件；神经网络法[11-12]综合考虑各影响条件，但其对数据量要求较高，极易过度学习，普适性差。基于此，提出梯度提升（GBRT）算法来预测支架阻力，避免了以上方法的不足。但模型的预测精度和泛化能力受参数的影响明显，因此采用改进的逻辑斯谛（Logistic）算法对参数进行优化，建立支架阻力预测的LR-GBRT 模型。

1 研究方法

1.1 基于逻辑斯谛算法的特征选择

逻辑斯谛是1 种速度快，能够快速吸收新数据并更新模型的适合分类问题的算法模型[13]。选择该模型对样本进行特征预处理。对于样本训练集A=（xi，yi），i=1，2，3，…，N，其中：xi，为影响支架阻力yi的特征向量，单个样本训练集的代价函数（cost function）cost（hθ，y）为：

在L2中选择权值系数之差小于0.5 的阈值，L1中选择其权值为0 的特征集组合成1 个新的集合，并将L1中的权值平均分配给该新集合中的特征值。将经过L1和L2正则化后的数据集作为梯度提升决策树的原始数据进行回归预测。

1.2 梯度提升决策树算法

GBRT 在每次迭代时通过对其损失函数最小化，在残差减少的梯度方向上新建立1 棵弱决策树。最后将所有的弱决策树累加起来得到强决策树得到最终预测结果[14]。

将液压支架的阻力用y 表示，影响液压支架阻力的变量用x 表示，N 表示用于训练的样本数。算法过程如下。

1.2.1 定义算法中默认的损失函数L（yi，f（xi））

式中：f（xi）为预测液压支架阻力值，i=1，…，N。

初始化强学习器f0（x）为：

式中：ρ 为只有1 个根节点的树，来估计使损失函数极小化的常数值。

1.2.2 迭代m＝1，2，3，…，M 次后的负梯度值

式中：I 为指示函数，满足条件x 落入叶子节点区域时取1，否则取0。

该算法最终模型由数个子模型集成所得，当模型训练速度较大时，会忽略一些样本信息,容易过拟合。基于此，加入参数来控制子算法模型的学习速率，则式（7）变为：

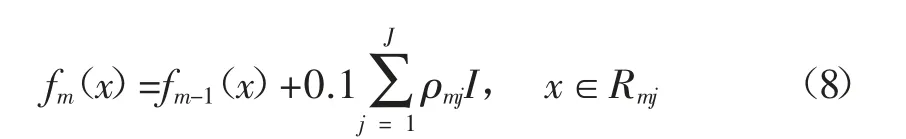
1.2.3 M 次迭代后得到集成算法模型

根据上述分析以及树的最大分裂节点和最大树深关系，选取树深3 为GBRT 树深参数。LR-GBRT算法流程图如图1。

图1 LR-GBRT 算法流程图Fig.1 Flowchart of LR-GBRT algorithm

2 液压支架阻力预测模型的建立与评价

2.1 影响因素以及样本选取

选择样本数据首先应确定所研究问题的影响因素。根据前人研究表明，影响工作面支架阻力的主要因素有[15-17]：煤层埋深、工作面长度、顶板岩石抗拉抗压强度、顶板厚度、来压步距。样本选择时数据应选取代表性样本，避免数据集中化，样本越具有代表性，模型越具有普适性。在通过现场调研及文献查阅，选取43 组具有代表性的浅埋煤层工作面数据。其中，随机选取28 组作为训练数据，15 组作为预测数据。部分数据见表1。

表1 部分数据Table 1 Partial data

2.2 模型的建立与评价

为消除参数的量纲不同对预测精度的影响，调用Python-Sklearn 库的Proprocessing.MinMaxScaler函数进行归一化处理。

为验证基于LR-GBRT 预测模型的预测能力，搭建并调试决策树（DTR, 树深取3）、线性回归（LR）、弹性网回归（ENR）以及支持向量机（SVM,核函数取rbf，C=1×103，γ=0.2，其中，C 是惩罚系数，即对支架阻力预测结果误差的宽容度，γ 为rbf 核函数自带参数，该值决定了预测后的支架阻力数据映射到新的特征空间后的分布）等常用算法的预测模型至最优状态，并用训练样本集分别训练以上模型进行预测比较。

为了验证各模型的阻力预测结果，采用平均绝对误差（MAE）、均方误差（MSE）和拟合度（R2）3 个指标来评价各模型在测试集上的预测效果，其中平均绝对误差和均方误差越接近0，拟合度越接近于1，说明模型拟合性能越好，支架阻力的预测准确率越高。

式中：yi为第i 个测试样本的支架阻力真实值；为其对应的支架阻力预测值；为测试样本均值；i＝1，2，3，…，N；N=45。

为获取预测支架阻力的3 种指标值，减少随机误差，采用了10 折交叉检验法[18]来总体评价模型的预测能力。在k 折交叉检验中（本文取10），样本被分割成k 个大小相等的样本子集，保留1 个子样集作为验证数据，剩余k-1 个子样集训练模型，将该过程重复k 次，每个子样本仅用作验证数据1 次。最后，将来自每次所得结果值进行平均，可得到1 个总体性能评价指标。

2.3 预测结果分析

基于支架阻力训练样本集，对上述各算法模型调试至最优态，将其在测试集上的支架阻力预测结果同实际阻力值进行比较，预测模型结果如图2。

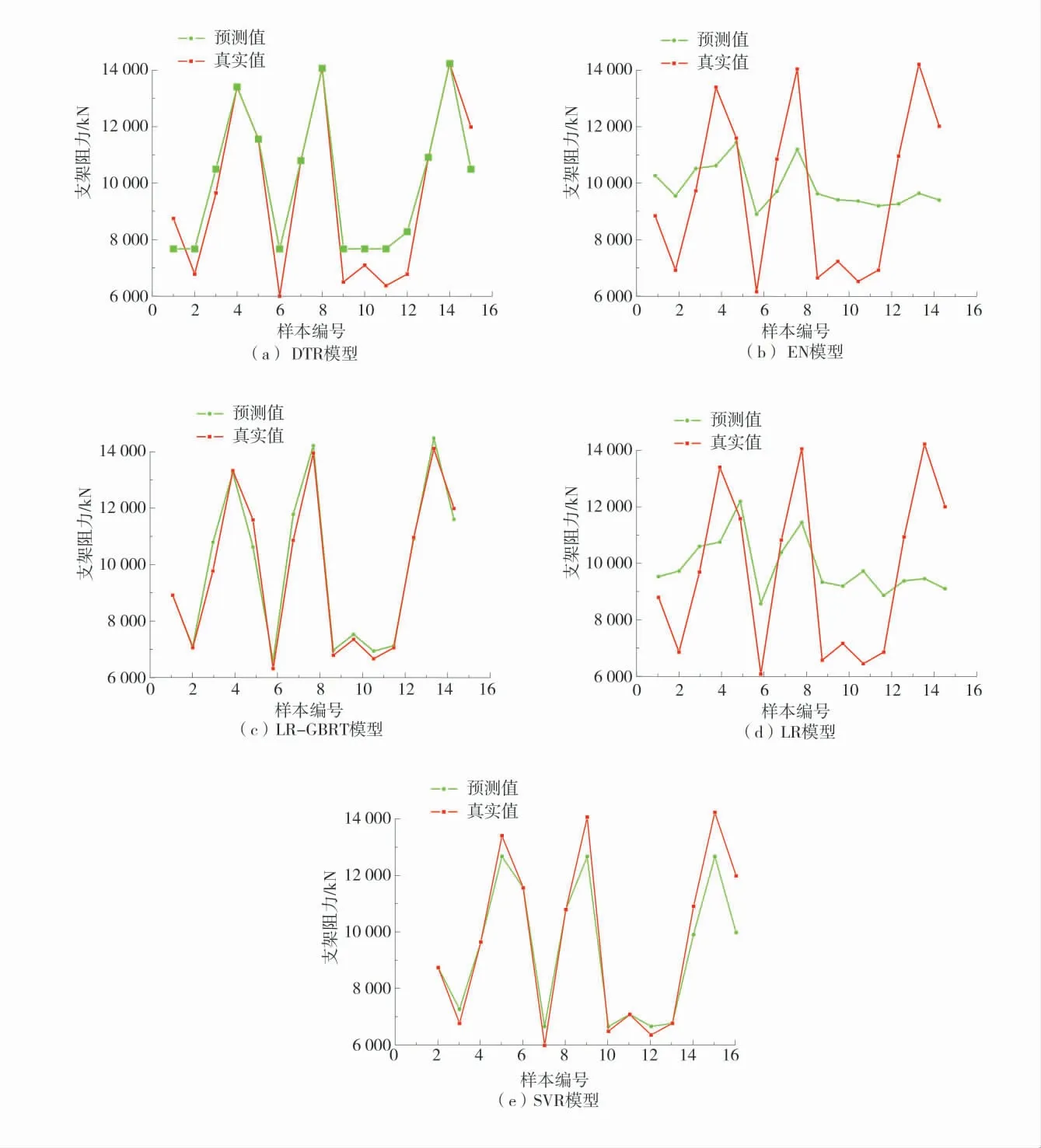
图2 预测模型结果Fig.2 Prediction model results

由图2 可知，DTR 和SVR 的拟合趋势较好，偏差相对较小；LR 和EN 误差相对较大，原因可能是因为用于训练的数据集较少；LR-GBRT 预测模型对数据预测效果最好，拟合度高，更适用于小样本数据情况；6 折交叉验证结果见表2。表2 结合不同评价指标描述了上述预测模型在测试集上的支架阻力预测性能。对比模型交叉验证结果可知，LR-GBRT的可解释变异和拟合度相较于其它4 个模型的值最接近1，均方误差和平均绝对误差的值相较于其它4个模型值最小。LR-GBRT 模型表现最优，体现了LR-GBRT 回归模型在预测液压支架阻力上具有较好的预测精度。由此也可看出，支架阻力同各影响因素支架具有复杂的非线性关系特点。

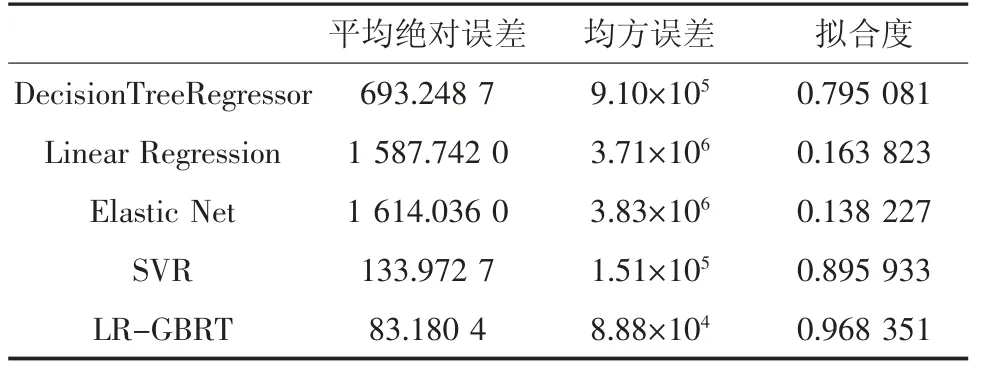
表2 6 折交叉验证结果Table 2 Results of 6-fold cross validation

3 工程应用

Qt 是C++跨平台应用程序框架，该框架受到广泛应用。例如，Itasca 公司在该框架下开发了FLAC、PFC 以及UDEC 等多款数值模拟软件。Python 同其结合为PyQt，在PyQt 环境下，将训练好的模型封装并进行GUI 开发，以便工程实际应用。

为了验证开发后的系统在预测最大液压支架阻力的实际效果，分别对南梁煤矿1-2煤工作面和韩家湾煤矿3302 工作面采用在线式KJ513 型矿压监测系统在工作面上部、中部和下部分别布置3 条测线，以工作面距开切眼100 m 位置处开始观测。工作面上中下3 部分支架工作阻力随工作面推进的变化曲线如图3。在此过程中南梁矿发生12 次周期来压，韩家湾矿发生10 次。最大来压分别为8 439 kN和12 003 kN，GBRT 预测结果分别为9 024 kN 和12 320 kN，工作阻力和预测最大阻力比值分别为：93.5%和97.4%，实践证明，该系统能较好的对液压支架阻力进行预测，达到现场应用要求。

4 结 论

1）基于梯度提升理论，通过选取煤层埋深、工作面长度、覆岩抗拉抗压强度、直接顶厚度和来压步距等7 个主要影响因素作为液压支架阻力选型的判别指标，结合43 组浅埋煤层样本数据，利用Python3.6 建立了液压支架阻力预测的GBRT 模型，并限制其学习速率，防止模型过拟合。

2）利用DTR、SVR、EN、LR 和LR-GBRT 构建的预测模型，对样本的支架阻力预测进行交叉检验以检验其可靠度。结果表明，用LR-GBRT 模型预测本文样本的拟合度最高，同比其余4 种算法具有较高的精确度。可见，该模型对预测支架阻力是行之有效的，它为支架阻力的选型确定提供了1 条新途径。

图3 支架工作阻力随工作面推进的变化曲线Fig.3 Variation curves of support working resistance with working face advance

3）基于PYQT 进行GUI 开发，能更好的将其应用于工程实践；需要指出的是，该于液压支架阻力的预测中还只是初步尝试，模型的预测结果很大程度上取决于指标的选取。今后的研究工作中，将进一步研究影响支架阻力的因素，如构造应力、地下水作用以及掘进速度等，考虑更多的影响因素并建立云数据平台囊括更多数据，以期进一步增强模型的泛化能力，为支架阻力选型提供1 个新途径。