减速板故障下的RLV末端区域能量管理算法设计

权申明，王松艳，晁 涛，杨 明

(哈尔滨工业大学控制与仿真中心，哈尔滨150080)

0 引 言

可重复使用飞行器(Reusable launch vehicle，RLV)的末端区域能量管理阶段(Terminal area energy management，TAEM)位于再入飞行阶段之后，自动着陆阶段之前，是衔接再入段和着陆段的重要过程。一般来说，飞行器长时间处于再入飞行阶段，由于气动环境的不确定性，TAEM初始状态中位置、速度存在偏差。在整个TAEM过程中，发动机无法提供动力，需要依靠自身运动状态进行能量的控制。为了保障飞行器的安全着陆，TAEM算法应在终端时刻将飞行器控制在自动着陆段所要求的初始窗口范围内[1]。

TAEM通过调节能量变化规律，改变飞行器高度、速度以及倾角的变化规律，安全到达着陆窗口，满足着陆所需各种的条件。通常情况下，TAEM阶段中由于初始和终端位置相对固定，有三种方法进行能量控制：1) 增加飞行距离进行速度耗散，一般需要设计航向校准段圆心位置和转弯半径两个参数[2]；2) 调制动压，通过改变飞行高度与速度的关系进行能量调节[3-4]；3) 调制速度制动，通过减速板直接对飞行器速度进行调节。整个TAEM过程一般包含捕获段、航向校准段(Heading alignment cone，HAC)和进场前飞行段三个阶段，每个阶段有各自的任务。

现阶段的TAEM制导算法研究主要包括两部分内容：轨迹设计与制导跟踪。早期的TAEM轨迹设计方法大多在分离的二维平面内进行离线设计[1-2,5-7]，能够适应小范围的侧向机动需求，同时对飞行器的初始状态要求严格，因此适应性较差。部分学者结合蛇形机动形式，优化得到三维机动飞行轨迹，但本质上仍为二维轨迹设计方法[3]。

随着轨迹设计算法的不断发展和计算机水平的提高，三维的在线计算方法不断提出[8-13]，能够根据飞行器的实际状态进行在线轨迹设计，具有较强的适应性。张恒浩[8]提出一种快速生成算法能够自动选择直接进场或者间接进场策略，通过不断迭代校正计算得到HAC的中心位置与终端半径以调节航程。文献[9]采用增加直线预测捕获段的方式，然后求解存在动压、过载约束情况下的非线性规划问题，得到最优HAC中心位置。Lan等[10]则重点研究了飞行器倾侧角受限情况下的三维轨迹在线规划方法，并考虑了纵向、侧向两个平面运动的耦合，实时规划出三维飞行轨迹。刘智勇等[11]通过航程预测在线生成轨迹，给出了减速板角度偏转规律和高度/航程联合调节方案。

然而，在TAEM过程中，减速板由于突发故障可能会导致飞行任务难以完成，甚至威胁到相关人员的安全，前述控制系统设计中尚未考虑。针对减速板故障导致无法到达着陆窗口的问题，本文提出一种考虑减速板故障下的在线的RLV末端区域能量管理算法。首先结合纵向能量走廊和地面侧向几何轨迹，得到标称飞行轨迹。然后分析了动压剖面对飞行轨迹的影响，主要为动压选取与飞行距离的关系，在此基础上，设计在线修正动压剖面策略，将传统的动压剖面四参数求解简化为单参数更新问题，提高了计算效率。同时，证明了动压剖面单参数更新的可行性。仿真结果表明，所提出的TAEM算法能够控制飞行器安全到达自动着陆窗口，具有一定的鲁棒性。

1 模型描述

为了简化分析过程，可以忽略运动学和动力学方程中的次要项，并假设高度随时间变化率等于地心距随时间变化率，根据牛顿第二定律及运动学关系，建立TAEM段飞行器三自由度运动方程。

(1)

式中：h,λ,φ,v,θ,σ为质心运动方程的状态量，分别表示飞行高度、经度、纬度、飞行速度、速度倾角、速度偏角，Sref为参考面积，Ma为飞行马赫数，q为飞行动压，g为重力加速度，CL和CD分别为升力系数、阻力系数，倾侧角γc以及攻角α和减速板角度δe为质心运动方程的控制量。同时，为了提高计算效率，以上各物理量可采用归一化处理，归一化过程不做详述。

2 TAEM标称轨迹设计与轨迹跟踪

2.1 纵向标称剖面设计

能量走廊体现了RLV飞行过程中具有的能量与动压、过载约束及升阻特性之间的关系，是飞行器安全飞行的区域。待飞距离是飞行器沿着地面投影从当前飞行状态到终端位置的剩余飞行总长度，因此可以通过直接设计地面几何轨迹得到待飞距离的大小。在能量走廊中选择一条曲线作为能量剖面，该曲线是待飞距离的函数。结合飞行器的飞行能力，沿着最大动压飞行得到最陡下滑剖面得到能量走廊上边界(通常飞行距离最短)，保持最大升阻比飞行得到能量走廊下边界。因此，首先需要求出能量走廊的边界，进而在其中设计合适的标称能量剖面。

飞行器的机械能为

(2)

定义飞行器的单位重量能

(3)

式中：W=mg为飞行器的重量。TAEM阶段飞行器无动力飞行，无质量变化，假设重力加速度g不变，则E与EW是等价的。记R为待飞距离，则单位重量能EW随航程的变化率为

(4)

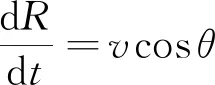
(5)

可以看出，飞行器受到的阻力越大且航迹倾角幅值越小，能量消耗越快。能量走廊可以通过飞行试验或者理论分析得到，对于相同的初始能量状态，选取不同的动压剖面边界构成了能量走廊。

进行纵向轨迹离线设计时，通常忽略侧向运动的影响，令倾侧角为零得到

(6)

由于飞行器受到物理结构的限制，需要对飞行动压进行限制。在TAEM无动力飞行过程中，高度逐渐降低，大气密度增大变快，速度损失较快，而动压是速度和高度的函数，因此其变化相对缓慢。动压改变后，阻力、速度倾角均会发生变化，最终改变能量变化规律。此外，调节动压剖面相比直接调节速度会产生更加稳定的效果。

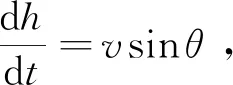
(7)

假设动压-高度剖面已知，便可得到动压随高度变化规律，给定任一高度便可求得CL和CD，进而得到纵向运动的其它状态量。

动压剖面是将动压随高度变化设计为分段的三次多项式，其中c0,c1,c2,c3为待求参数。

q(h)=c0+c1h+c2h2+c3h3

(8)

那么动压随高度变的变化率为

(9)

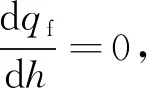
(10)

通常情况下，TAEM初始高度为h0=25 km，终端高度h0=3 km，取hmid=14 km时，h0≠hf≠hmid≠0，则上式右侧方阵的行列式值不为零或者极小值，其逆存在。

通过选取合适的动压剖面，进而求得纵向运动状态。设计动压剖面时需要注意飞行器结构能力的限制，在初始和终端动压满足的同时，过程中任意时刻均不可超过动压约束边界[7]。动压的大小会影响飞行距离，可以根据以上的原则选取合适的动压剖面。采用图1所示流程进行能量走廊设计：

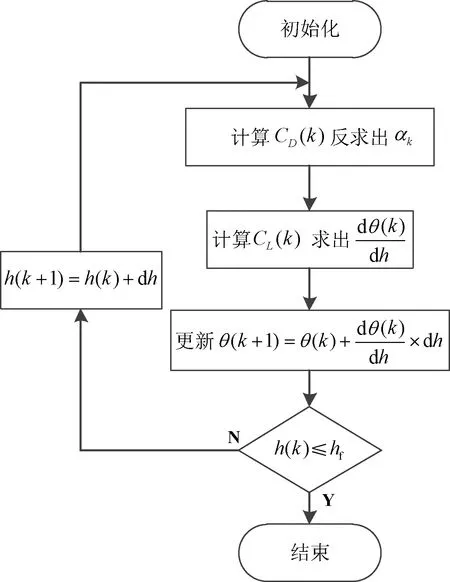
图1 能量走廊计算流程图Fig.1 Flowchart of energy corridor calculation

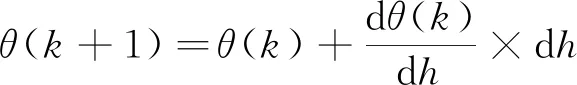
2.2 侧向几何轨迹设计

在侧向上，末端区域能量管理段地面投影轨迹示意图如图2所示：

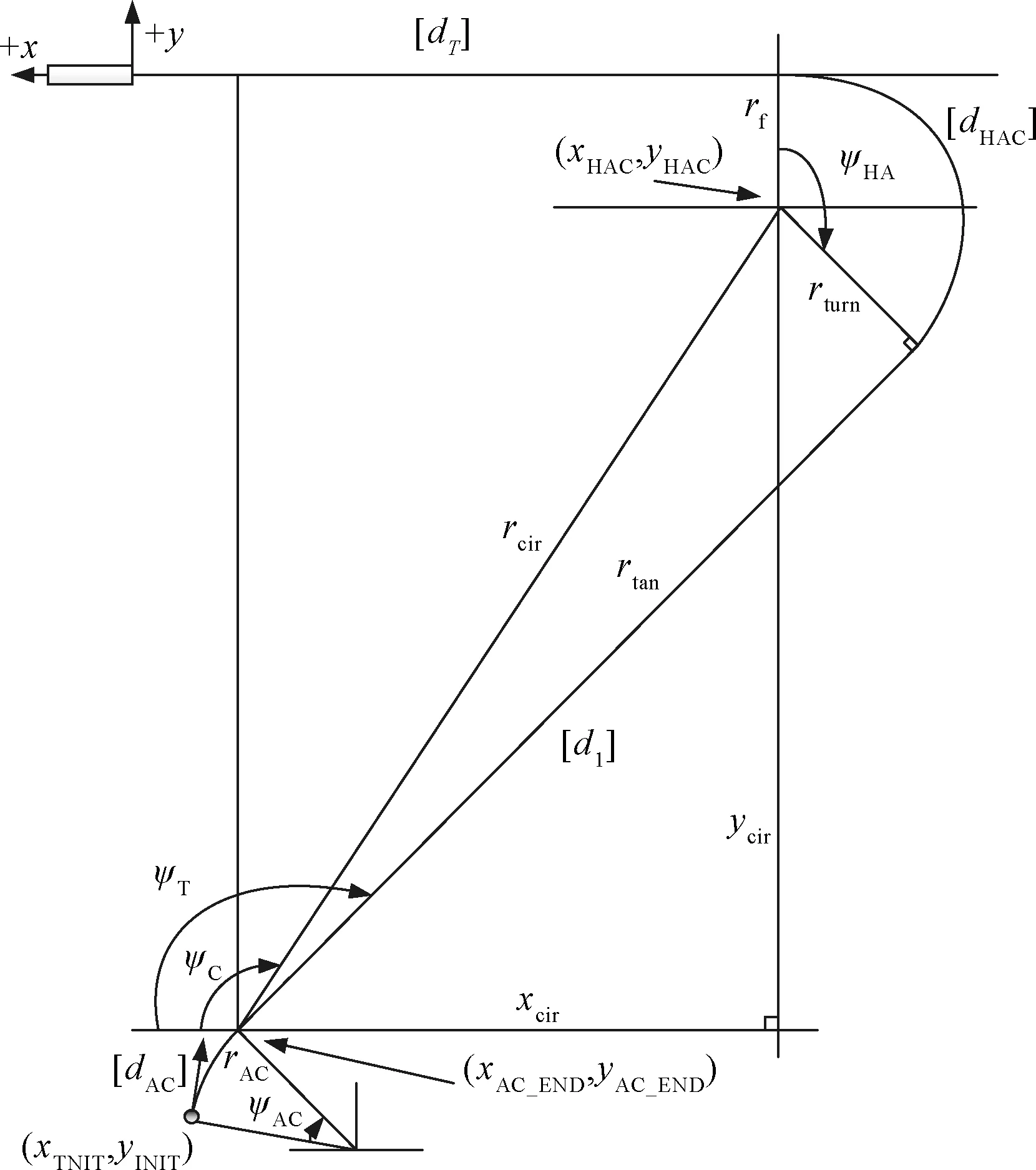
图2 TAEM段地面投影轨迹示意图Fig.2 Schematic of ground projection trajectory of TAEM phase

沿着轨迹从终点(原点)反向计算，最后一段为自主着陆段飞行轨迹地面投影，是沿x轴从HAC终点到终点条件的距离。飞行器在HAC转弯时的地面投影可以在极坐标下用半径rturn和转弯角ψHA表示。HAC的螺旋半径计算公式为

(11)

式中：rf表示最终转弯半径，r1和r2是常系数。

yHAC的位置计算为

yHAC=ySGNrf

(12)

式中：ySGN是飞行器该螺旋转弯段中心位置在跑道中心线两侧的标志。

沿HAC螺旋的弧长距离dHAC计算为

(13)

为了求出线段距离d1，首先用距离rcir计算转弯端(xAC-END,yAC_END)到HAC中心点的距离

(14)

xcir和ycir的按照以下公式计算

(15)

然后得到

(16)

式中：rturn为HAC起始点的HAC转弯半径，

同时可得

(17)

然后，指向螺旋开始时的HAC切线

(18)

可得初始航向误差角为

ψAC=ψT-ψ

(19)

则沿圆形段dAC的距离为

dAC=rAC|ψAC|

(20)

式中：转弯半径rAC可通过最大法向过载计算

(21)

地面轨迹距离之和为

rpred=dAC+d1+dHAC+dT

(22)

在某些条件下，dAC,d1或dHAC段可以为零。

2.3 有限时间轨迹跟踪控制器

轨迹设计为轨迹跟踪提供参考轨迹，一般情况下，TAEM段的制导从纵向和侧向两方面进行，TAEM中各个飞行阶段由于目的不同需要分别设计轨迹跟踪控制器。侧向上主要通过预测地面待飞航程进行倾侧角修正进行侧向轨迹跟踪。纵向上通过反馈高度偏差调节过载进行高度控制。

捕获段需要控制飞行器朝着HAC柱面初始切点位置飞行，以便飞行轨迹和HAC的表面某点相切，而后飞行器沿着HAC表面飞行的同时控制其能量大小。在进场前飞行段飞行器将沿着跑道中心线进行直线平飞到达自动着陆段接口处。

1) 捕获段

捕获段位于TAEM段的起始段，在捕获段阶段，飞行器轨迹的地面投影与HAC的位置、最终半径和螺旋系数三个因素有关，为了使飞行器飞行轨迹与HAC相切，倾侧角指令应与航向偏差角成正比。捕获段倾侧角指令为：

γc=GvΔψAT

(23)

倾侧角的计算如上式所示，Gv是控制器比例系数，ΔψAT是飞行器航迹偏角偏差。

2) 航向校准段

该阶段保证飞行器沿HAC表面飞行，并控制动压和速度制动的变化。假设飞行器以固定倾侧角γc进行飞行

(24)

飞行器在沿着HAC柱面飞行时不断进行航向修正，最终对准跑道。得到飞行器在航向校准段的飞行关系式如式(25)所示。

(25)

当飞行器需要沿HAC柱进行飞行时，参考倾侧角的计算公式如式(5)所示。

(26)

为了使飞行器更加精确地跟踪HAC柱的地面投影，将实际的倾侧角指令设为参考倾侧角的前馈输入与闭环反馈之和，如式(26)所示。式中Δr是转弯半径偏差，KR和KRD均为控制器比例系数。

3) 进场前飞行段

(27)

当飞行器在一定角度范围内对准跑道时，即进入进场前飞行段。上式中，Δy表示飞行器的实际位置与跑道轴线的侧向偏差，GR和GDR表示比例系数。

纵向上，控制飞行器跟踪标称动压曲线，动压相对于飞行高度和速度数值较大。因此纵向制导设计选用跟踪动压-高度剖面，以实现对飞行器速度的控制。

飞行器可以通过两种途径减小动压大小[6]：一种方式通过减慢飞行器降高速度，减小大气密度过快增加的影响；另一种方式可以增大阻力，快速消耗速度，但是这样会导致升力减小，飞行高度降低更快，因此方式二需要适当增加阻力，达到速度减小和高度降低的平衡状态。通过过载控制可以实现对动压的调节，在动压过大情况下，增加过载和升力，增大攻角值，所受阻力增加，减速效果增强。

(28)

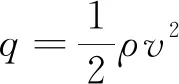
(29)

记x1=q，u=ny，且f(x1,u)=μ，将μ视为系统虚拟控制量，则式(29)可写为

(30)

期望动压值为qc，构造滑模面s=q-qc，针对μ，设计有限时间动压剖面跟踪控制器

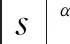
(31)

式中:k>0,0<α<1。根据文献[14]，容易得到该控制器的有限时间收敛特性。然后，通过法向过载ny=f-1(qc,μ)可以计算出攻角。

3 实时动压剖面修正算法

3.1 算法设计

由于减速板发生卡死故障，因此可以通过转离跑道和调制动压这两种方式进行在线TAEM算法设计，计算流程如图3所示。

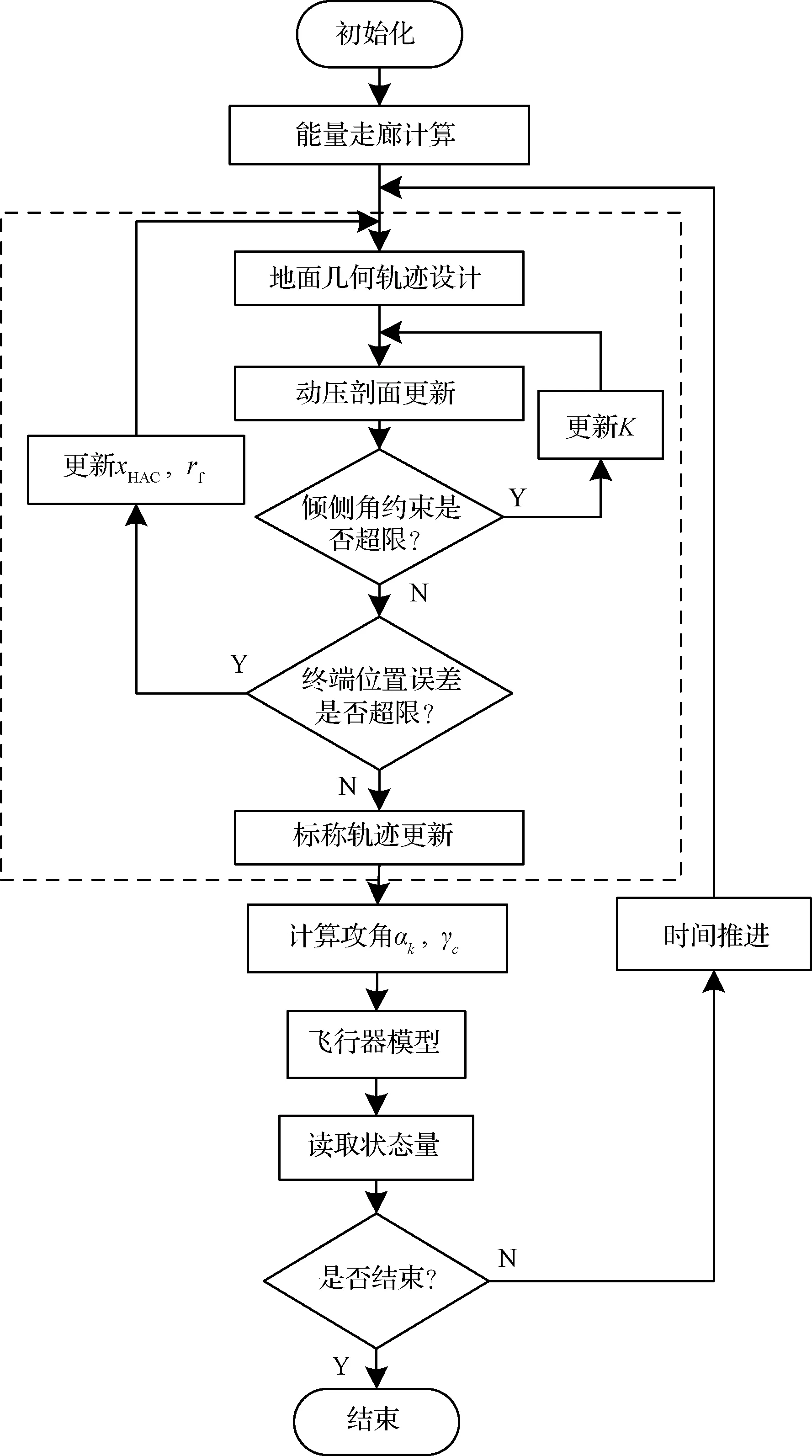
图3 TAEM段仿真流程图Fig.3 Flowchart of TAEM phase

由式可知，动压剖面的选取决定了飞行器的飞行距离及其他物理量变化规律，在标称剖面设计时，选取最陡下滑剖面和最大升阻比下滑的中值作为标称动压。为了进一步探究动压剖面对飞行器飞行能力的影响，改变标称动压剖面在动压剖面边界中的位置，利用下式进行计算。

(32)

此外，对于xHAC,rf的更新算法可采用倾侧角约束值与倾侧角最大值进行迭代计算，详细过程可参考文献[8,10,12]。

3.2 算法合理性分析

根据式，改变K值，做出反归一化后各状态量曲线如图4所示。

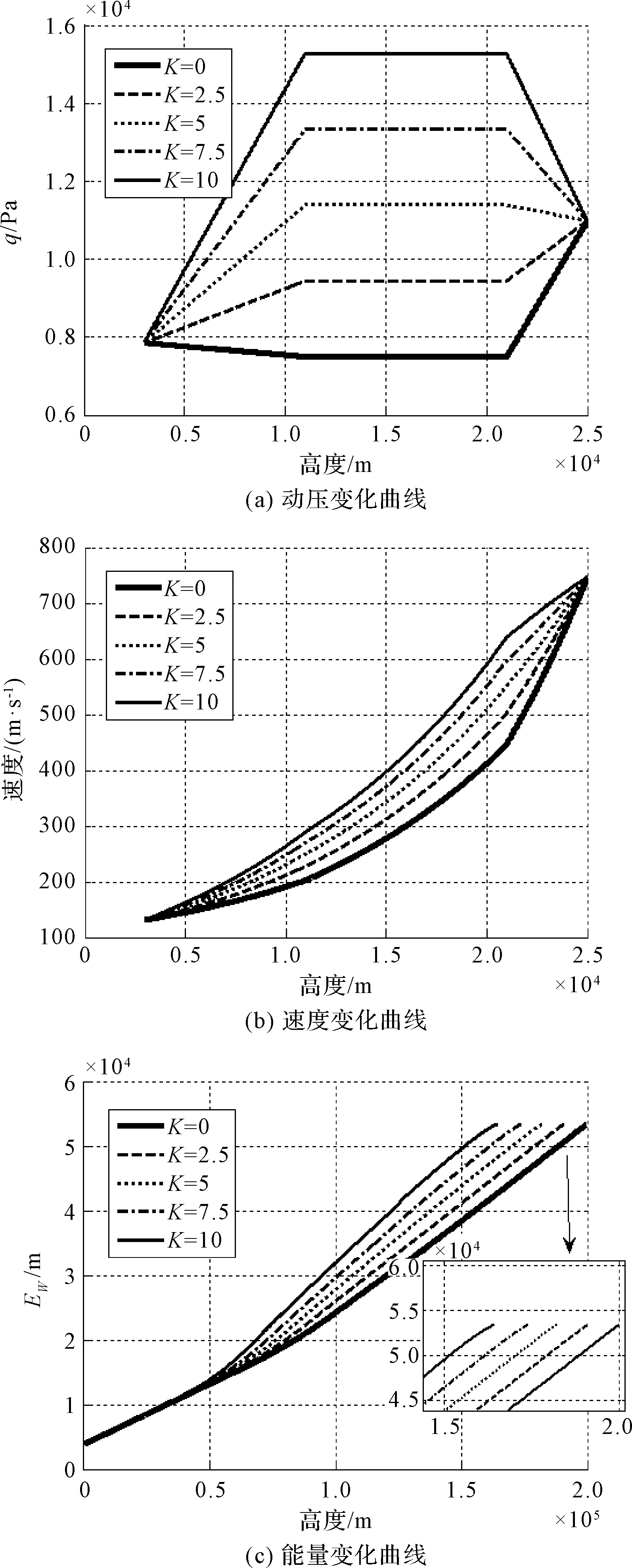
图4 状态量随K值变化曲线Fig.4 State curves with different K

通过图4可以看出，随着动压剖面的均匀变化，飞行器射程也近似均匀变化，这个特点可以为实时根据待飞距离更新动压剖面提供依据。图4(a)中可以看出，当K值增加时，动压剖面曲线上移，同一个高度下的动压增大，不同K值所对应的飞行速度减小，图4(b)，因此需要使用更大的攻角(幅值)来增加阻力系数，从而，减小飞行器飞行距离。从图4(c)可以看出，随着K的均匀增加，在能量走廊内，射程逐渐减小。

通过以上分析可以看出，飞行器动压剖面对飞行器射程具有很大的影响，由于飞行过程中存在较大不确定性及干扰，同时由于飞行器的橫侧向运动对纵向状态的影响，当标准动压剖面下的飞行距离小于实际待飞距离时，减小动压剖面的大小，飞行器，飞行高度增加，减小速度损耗，可以增加射程；当标准动压剖面下的飞行距离大于实际待飞距离时，增大动压数值飞行高度将会降低，加快速度损耗，可以减小射程。

图5给出了飞行器根据能量-待飞射程曲线，调节动压剖面的示意图，可以令

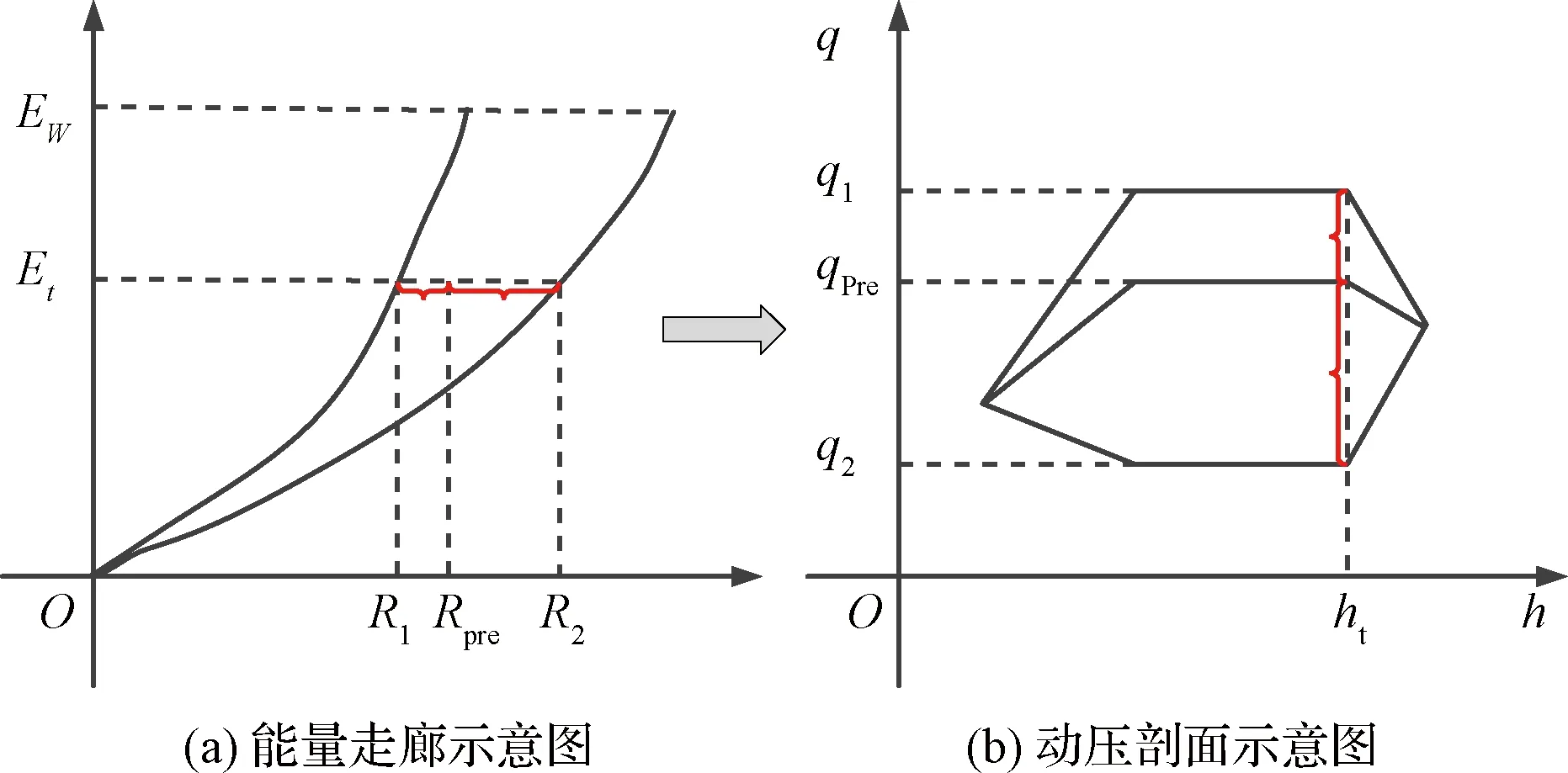
图5 动压剖面修正示意图Fig.5 Schematic diagram of dynamic pressure profile correction

(33)

具体来看，根据实时飞行器能量Et，以及期望待飞射程RPre，得到比例关系

(34)

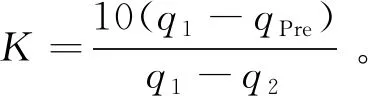
以下将通过变量关系证明该算法的合理性。

(35)

为了简化计算，可以假设飞行器的最近射程为原点R=0，并记

(36)

假设在TAEM过程中，θ<0，幅值和变化率均为小值，那么cotθ可以视为常值kθ。对于不同的动压曲线，由于初始和终端状态已经固定，q0和qf为定值。

(37)

由泰勒公式ln(1+x)=x-x2/2+x3/3≈x，对于归一化后的Δq(h)，可得

(38)

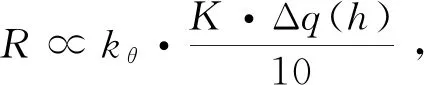
4 仿真校验

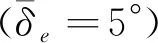
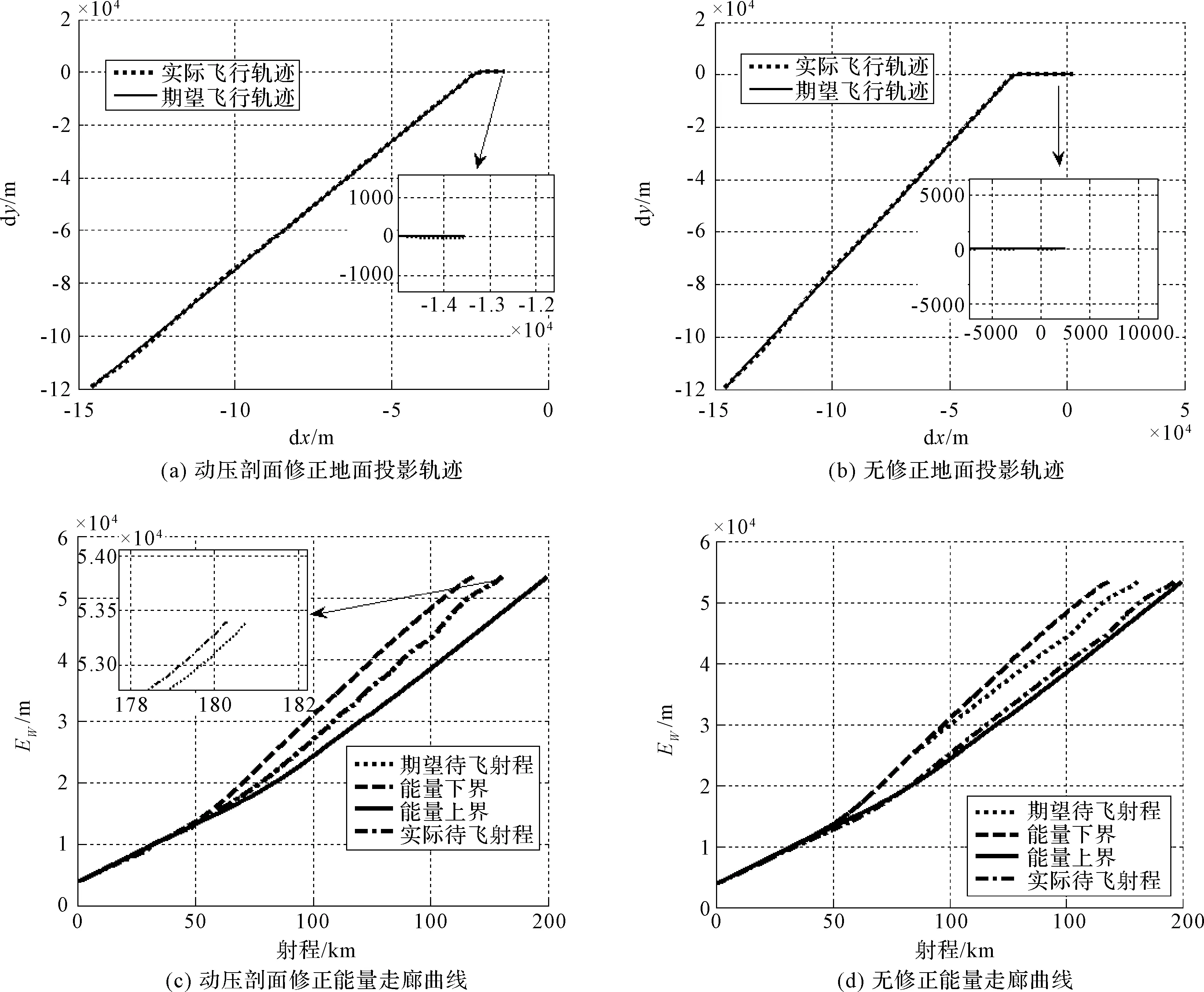
图6 气动参数摄动仿真结果Fig.6 Aerodynamic parameter perturbation simulation results

当升力系数摄动ΔCL=5%，阻力系数摄动ΔCd=-5%时，飞行器相同状态下升力增加、阻力减小，相比标称轨迹，飞行器具有更大的速度和能量，因此应该适当增加飞行器动压值，通过以上有动压剖面修正情况下的仿真结果，可以看出，在加入动压剖面修正后，飞行器能够以期望的飞行距离到达着陆窗口。

5 结 论

对于存在减速板故障下的RLV末端区域能量管理问题，本文给出了一种考虑减速板故障下的在线的RLV末端区域能量管理算法。通过纵向能量走廊和地面侧向几何轨迹，得到标称飞行轨迹。当存在减速板卡死故障及参数不确定性时，设计在线修正动压剖面策略，将传统的动压剖面四参数求解简化为单参数更新问题，提高了计算效率。仿真结果表明，所提出的算法能够到达着陆窗口，具有一定的鲁棒性。