断溶体油藏油源深度对井温分布影响的数值模拟

胡文革，邹宁，李丹丹，黄知娟，雷健，郭宇航，潘保芝

(1.中石化西北油田分公司，新疆 乌鲁木齐 830012； 2.吉林大学 地球探测科学与技术学院，吉林 长春 130026)

0 引言

塔河油田位于塔里木盆地塔北隆起阿克库勒凸起的南部斜坡区[1]，在该区域发现了断溶体油藏[2]。断溶体油藏的储集空间是中—下奥陶统碳酸盐岩层中沿断裂发育的大型洞穴、裂缝及沿缝溶蚀孔洞，物性圈闭是外围致密碳酸盐岩构成的侧向封挡[3]。断溶体油藏的石油富集差异化明显，不同油藏开发效果差异较大，开发井“高产不稳产”，产油深度难以确定[4]。

在断溶体油藏开发过程中，由于缝洞系统发育，钻井时常发生大量泥浆漏失与钻具放空的情形。在钻遇大型溶洞时往往封堵效果很差，这时无法继续钻进，而被迫完井。常规测井在漏失段和坍塌段都无法测量，导致生产时油源深度难以确定[5]。

无论井眼条件如何，都可以测量井内温度剖面[6]。井温测井是重要的生产测井方法之一，通过测量某一深度的井温或沿井剖面的温度变化，来确定生产油层的深度，了解井内流体的流动状态。油气生产过程中，井中温度不仅仅反映测量层段的温度信息，还受流体来源层段的温度影响[7]。在关井后非生产时段，井筒中的温度逐渐与地层温度相同，这时的井温称为静温；产液过程对井筒和地层温度分布产生影响，在稳定生产时的井温，称为流温[8]。

由于井筒和地层温度分布受到流体流动的影响，在断溶体油藏生产过程的温度场模拟中，需要同时考虑流动和能量传递，将温度场和流动场耦合计算。井中流体和周围地层通过传导、对流和辐射进行热交换，其中辐射作用很小可以忽略[9]。作为断溶体油藏主要的储集空间和生产通道，大型溶洞、裂缝以及井筒中的流体流动不遵循达西定律，而是具有管流特征，满足 N-S方程，因此流体动力学是研究断溶体油藏流动的基础[10-13]。

计算流体力学(CFD)是研究流体流动和能量传递规律的一种实用方法，利用离散方程描述连续的流动场和温度场，通过数值方法求解整个计算区域的流体性质[14]。相应的CFD商业化软件可以实现模拟过程的可视化和参数精准检测，其中COMSOL软件具有强大的流体流动分析能力和多场耦合计算能力。

断溶体油藏是一种新型的石油富集圈闭，对该类油藏的温度分布规律尤其是生产时流温的评价方法还是空白。利用COMSOL软件，模拟断溶体油藏的石油生产过程中温度场的变化，进行流体流动场和温度场的耦合，分析不同井筒和溶洞关系时井中流温、静温曲线特征。为利用井中静温和流温差异研究储层与井筒的相对位置提供依据，为断溶体油藏的开发提供帮助。

1 数学物理模型及模拟方法

本文模拟的断溶体油藏生产过程为：①初始状态时，石油储存在溶洞中，温度分布就是地层原始温度；②钻井开发时，石油以一定的速度从溶洞进入井筒，井筒和周围地层的温度场发生改变，井中温度为瞬态温度；③稳定生产一段时间，井中温度分布达到稳态，不再变化，测得的井中温度为流温曲线；④关井一段时间后，井中温度逐渐恢复到与地层原始温度一致，流体静止，此时为静温。在热平衡建立的过程中，热量在井筒与地层中的传递存在5个典型阶段，分别为：原始温度分布被破坏、热量在井筒内做稳定径向导热、热量从井筒向地层传递、热量在地层内做径向导热以及达到热平衡[15]。本文模拟采取稳态方法，不考虑生产时间和关井时间的影响，直接得到流温、静温曲线。

1.1 物理模型

塔河油田的断溶体油藏规模与断裂的发育密切相关[16]。图1是断溶体油藏在地震图上的形态，可以看出沿着断裂的走向分布的众多溶洞，这些溶洞具有不同的形态。图中标出了3口井的位置,这3口井均与溶洞直接接触[17]。唐海[18]通过分析钻遇溶洞和地震等资料，总结得到了5 种典型的断溶体油藏形态，每种形态由不同数量和大小的溶洞构成。这些溶洞水平方向较窄，垂向延伸很深，在几何上接近于圆柱，由此本文模拟时采取圆柱形的溶洞形态。

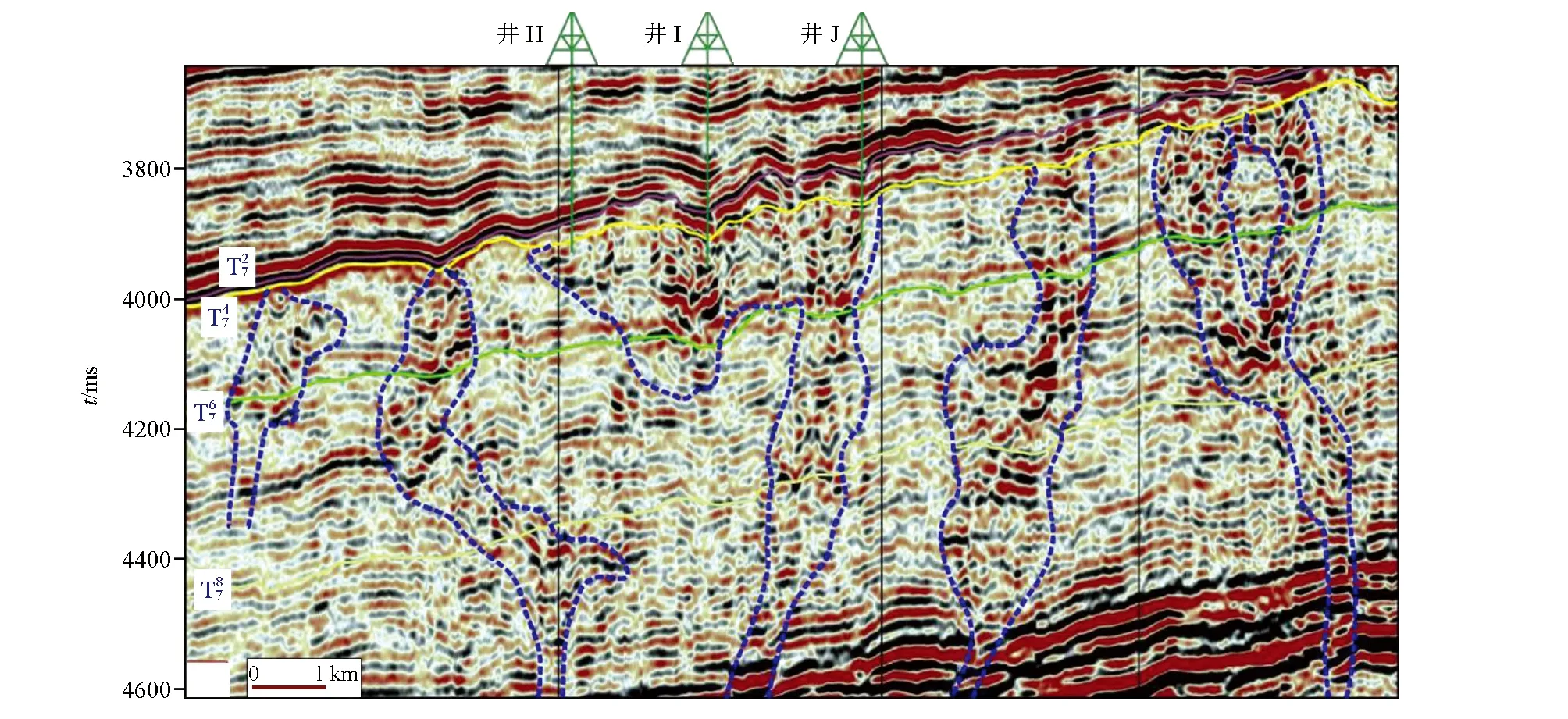
图1 沿断层的地震图像(图中蓝色虚线区域为溶洞[17])Fig.1 Seismic image along the fault(The blue dotted line area in the figure is karst cave[17])

考虑到生产井与油藏的相对位置存在的多种情况，文中确定了4种模型：①只有井筒(图2a)；②井筒与溶洞直接相连(图2b)；③井筒与溶洞通过裂缝相连，溶洞在下方(图2c)；④井筒与溶洞通过裂缝相连，溶洞在井底上方(图2d)。根据研究区地震剖面等资料确定了模型的几何参数(图2)，溶洞高为1 000 m，直径为100 m，钻孔直径为0.15 m，裂缝宽度为0.05 m。

图2 物理模型示意Fig.2 Schematic diagram of physical model

1.2 计算方法

利用COMSOL软件的流体传热模块进行稳态模拟。假设井筒、裂缝和溶洞中的流动为层流，地层为固体无流体流动，地温梯度恒定，不考虑热辐射。

通过数值计算和图像显示，对包含有流体流动和热传导等相关物理系统进行分析。文中基于CFD采用的基本算法是：用有限个离散点上的温度和速度的集合表示速度场和温度场，通过守恒方程组建立这些离散点上两种场变量之间的代数关系，然后求解代数方程组获得各个离散点上的温度和速度的近似值。

1.2.1 控制方程

在断溶体油藏生产过程的数值模拟中，流体的流动和传热受质量守恒、动量守恒和能量守恒方程控制。

1)流体流动方程

动量守恒

ρ(u·)u=·[-p+μ(u+(u)τ)]+F

(1)

质量守恒

ρ·(u)=0 。

(2)

2)传热方程

能量守恒

ρCρu·T+q=Q，

(3)

q=-kT，

(4)

式中:ρ为流体密度，kg·cm-3；u为流动速度，m·s-1；μ流体粘度，Pa·s；p压力，Pa；Cρ为恒压热容，J·(kg·℃)-1；q热通量，W·m-2；k为导热系数，W·(m·℃)-1；T为温度，℃；F表示体积力，Q表示热源。文中不考虑重力等的影响，F=0；没有内部热源，Q=0。

1.2.2 边界条件

地层的外边界保持原始地温分布，TΩ=T0+gT·h；

流动入口在溶洞底部，Tin=T0+gT·h，uin=ν；

流动出口在井筒顶部pout=0；

式中：TΩ为地层边界温度，℃；T0地面温度，℃；gT为地温梯度，℃·m-1；h为地层深度，m；Tin为入口处流体温度，℃；uin为入口处流体速度，kg·s-1；ν为流体流入溶洞速度，kg·s-1；pout为出口压力，Pa。相关的模拟参数见表1。图3为原始地温分布图，代表了静温的分布。

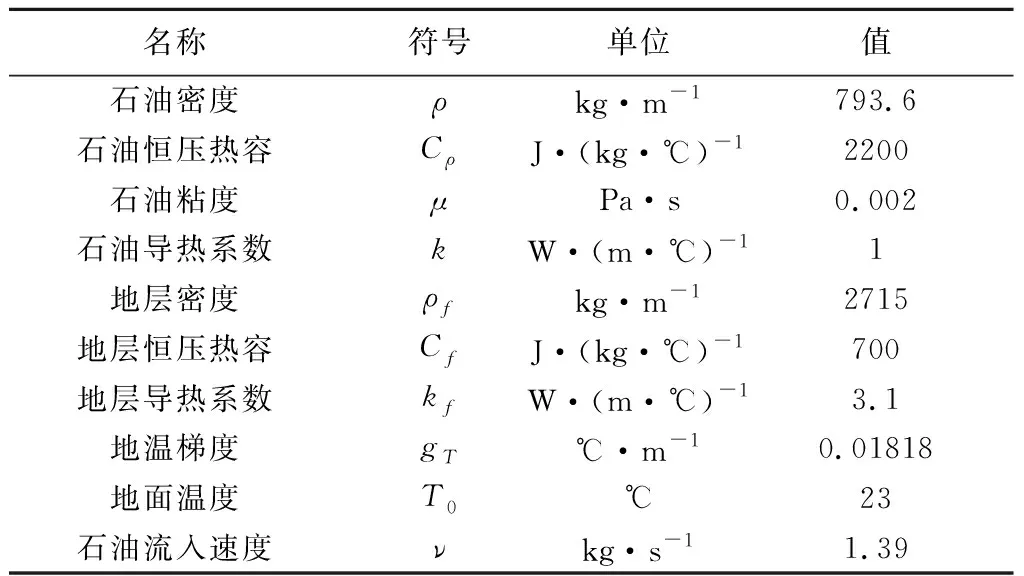
表1 模拟参数

图3 地层的初始状态Fig.3 Initial state of formation

1.3 模拟方法

1.3.1 网格剖分

在数值模拟中，物理模型的网格剖分精度对于计算结果有重要影响，COMSOL软件自带的网格剖分模块具有强大的功能，可以适应各种复杂模型。网格的剖分越细，模拟结果越精确，但是会增加网格数量，导致计算机内存需求和运算时间的增加[19]。由于井筒直径、溶洞直径与地层直径的几何尺寸相差较大，本文采取分区域的网格剖分方法，即井筒、溶洞、裂缝和地层等不同区域的网格大小不同。将井筒、裂缝和溶洞部分的网格进行更密集的剖分，而地层部分采取较粗的剖分，通过在不同区域的连接处设置边界层实现地层与井筒等的耦合，图4为其中模型4的网格剖分。

a—整体剖分网格;b—溶洞和井筒的局部网格a—global;b—karst cave and wellbore

1.3.2 温度场求解方法

由于石油流动和温度场相互影响，在模拟中需要考虑温度场和流动场的耦合问题。本文采用了COMSOL自带的稳态分离式求解器，该求解器在解决稳态多物理场问题时有良好的效果[20]。求解步骤如下：首先假设初始的压力分布求解方程(1)得到速度分量；再将速度分量代入方程(2)，检验速度求解是否正确；如果正确，将速度分量代入方程(3)和(4)求解温度场；如果不正确，使用压力修正，重新计算速度，直到得到满足精度要求的解(具体的计算过程参见文献[21])。

2 模拟结果分析

图5是只有井筒时(模型1)的温度分布和井温曲线。模型参数如下：井筒直径0.15 m，地层直径600 m，井筒长度1 000 m，井底位置在7 000 m。石油自井底流入井筒，流入时石油的温度与地层温度一致，此时井底流温和静温均为159.35℃。石油在井筒垂向热量对流传递效率远大于径向与地层的热传递。这样就导致生产时，井筒内的温度大于地层温度，高温石油将靠近井筒的地层加热，地层温度亦升高；稳定生产一段时间，地层温度和井筒内石油温度达到平衡，此时的温度分布如图5a和图5b，井筒内的流温曲线如图5c所示。可见流温与静温曲线在井底是一致的，向上流温逐渐大于静温。

a—温度分布切面;b—温度三维分布;c—井温曲线a—section diagram of temperature distribution;b—three dimensional distribution of temperature;c—well temperature curve

图6是溶洞在井筒下方时(模型2)的温度分布和井温曲线。模型参数为：井筒直径0.15 m，地层直径600 m，地层纵向厚度为2 000 m井筒长度1 000 m，溶洞直径100 m，长度1 000 m，井底位置在7 000 m，井底静温为159.35℃。石油在溶洞中流动时，由于与地层的接触面较小，且地层和石油的温差较小，溶洞中的石油冷却较慢，最终以较高的温度进入井筒，井底流温为 166.23℃。对比只有井筒时(模型1)的情况，存在溶洞时井底出现了较大的温度差异，且流温大于静温。

a—温度分布切面;b—温度三维分布;c—井温曲线a—section diagram of temperature distribution;b—three dimensional distribution of temperature;c—well temperature curve

图7是溶洞在井底下方，通过裂缝与井筒相连时(模型3)的温度分布和井温曲线。模型参数为：井筒直径0.15 m，地层水平方向长宽均为500 m，地层纵向厚度为2 000 m，井筒长度1 000 m，溶洞直径100 m，长度1 000 m，裂缝宽度为0.05 m，井底位置在7 500 m，井底静温为159.35℃。石油通过裂缝进入井底时的流温为161.74℃。对比只有井筒时(模型1)的情况，井底温度差异较小，流温略大于静温。对比井筒直接与井筒相连的情况(模型2)，模型3井筒中的流静温差较小。

a—温度分布切面;b—温度三维分布;c—井温曲线a—section diagram of temperature distribution;b—three dimensional distribution of temperature;c—well temperature curve

图8是溶洞在井底上方时(模型4)的温度分布和井温曲线。模型参数为：井筒直径0.15 m，地层水平方向长宽均为500 m，地层纵向厚度为1 600 m，井筒长度1 000 m，溶洞直径100 m，长度1 000 m，裂缝宽度为0.05 m井底位置在7 500 m，井底静温为159.35℃。由于溶洞在井底上方，温度较低的石油先向地层深部流动，逐渐被加热，但温度尚未上升到与地层温度一致即通过裂缝进入井筒。通过裂缝进入井筒时井底流温小于静温，井底流温为157.63℃。

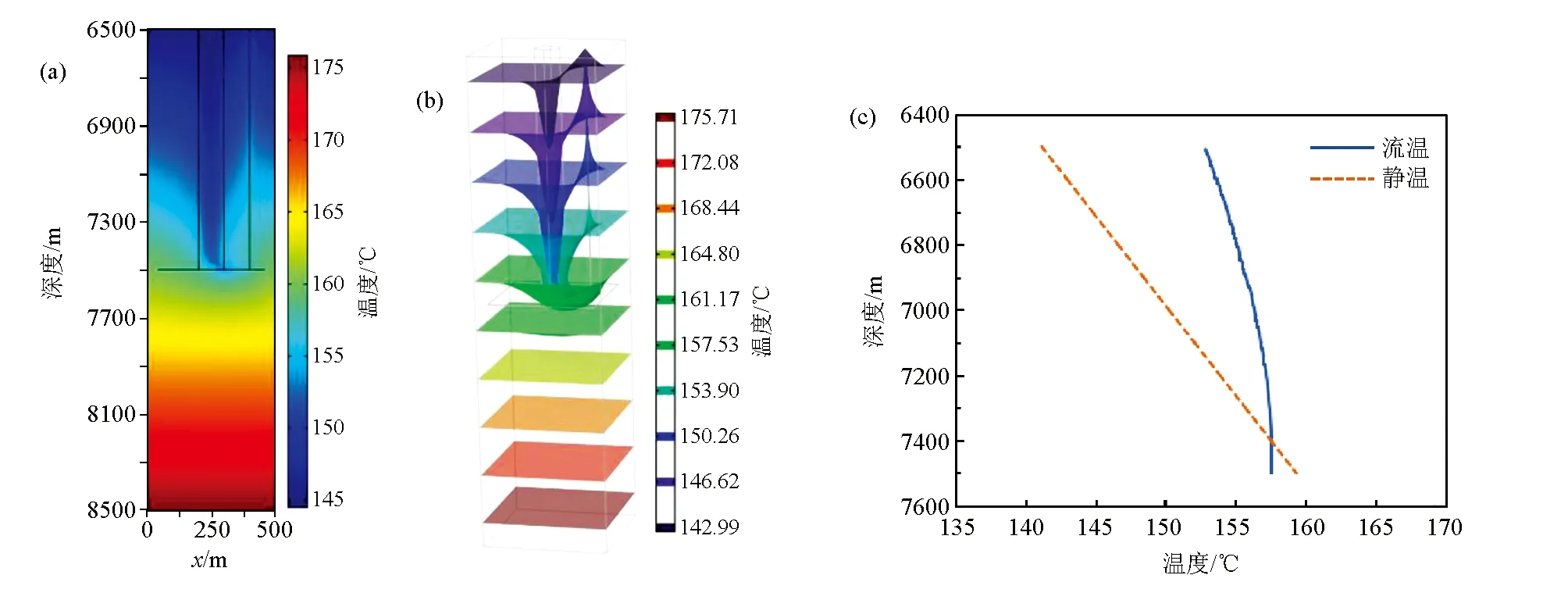
a—温度分布切面;b—温度三维分布;c—井温曲线a—section diagram of temperature distribution;b—three dimensional distribution of temperature;c—well temperature curve

3 实际井温分析

不同深度石油从溶洞进入井筒时的温度不同，测得的流温曲线也不同，图9是研究区A井和B井的实测和模拟流温、静温曲线，两口井在钻井和完井中均出现了泥浆漏失，目前均已稳定生产，产量约为90 t/d。使用表1的参数，结合已知的井底深度和产量数据，选择流温曲线形态相似的模型进行模拟。

图9 实测与模拟井温曲线对比Fig.9 Comparison of measured and simulated well temperature curves

结果如下：A井井底在7 400 m，温度160.114℃，此深度的静温为158.733℃，温差1.381℃，该井的流温曲线形态与模型1相似，模拟结果显示该井的油源深度在7 510 m。B井井底在6 950 m，此深度的实测流温为150.947℃，静温为146.56℃，温差4.387℃，该井的井底流静温差较大，形态与模型2的模拟结果相似，推断溶洞在井孔下方，依据油源深度为7 500 m时的模拟结果(图9b的蓝色实线)，推测该井的油源深度为7 500 m。

4 结论

断溶体油藏作为一种新型的石油富集圈闭，急需有效的测井评价方法，以确定储层深度。文中通过对不同井筒和溶洞相对位置设置不同的断溶体模型，模拟了受石油流动影响的温度场，发现利用井中流温、静温曲线可以确定断溶体油藏储层位置。当产油层位于井底时，井底的流温、静温一致；当石油产自井底上方时，井底流温小于静温；当石油产自井底下方时，井底流温大于静温。通过实测的流温与静温曲线的形态，可以推断合适的溶洞—井模型，结合油井的生产数据通过数值模拟计算出油源位置。在之后的研究中需要进一步确定流温曲线与油源位置的定量关系，以便更快捷地确定油源深度和溶洞大小等信息。