飞机客舱地毯清洗机的设计分析
2020-07-24董艇舰王亚楠
董艇舰, 王亚楠
(中国民航大学 1.考管中心;2.航空工程学院, 天津 300300)
目前飞机客舱地毯由人工清洗,传统的人工清洗不仅耗费大量的人力物力,而且工作效率极低,无法满足当今民航运输快速发展的要求。针对这一问题进行研究,提出并设计一款结构体积小、操作方便、成本低廉的专用于飞机客舱地毯自动清洗的机械,进一步来解决飞机客舱地毯清洗的压力,提高清洗的效率,降低清洗成本。
1 地毯清洗机的结构设计
航空地毯的尺寸通常为:长10 000 mm,宽350 mm。根据《中华人民共和国民用航空行业标准 MH/T 6060-2015航空地毯》4.1型号,按地毯单位面积的总质量(允许5%偏差),将地毯划分为以下型号:
Ⅰ型:小于1 660 g/m2;Ⅱ型:1 760 g/m2;
Ⅲ型:1 900 g/m2;Ⅳ型:不小于2 170 g/m2。
参考市场上常见的大型地毯清洗设备[1],清洗速度通常为0.5 m/min~2 m/min,现取清洗速度V=0.5 m/min,主轴转速为n=60 r/min。初步打算对地毯进行以下四个步骤[2]清洗:
除尘过程→清洗过程→漂洗过程→压干脱水过程
下面将分别介绍飞机客舱地毯清洗机的除尘、清洗、漂洗、压干脱水这四个过程的结构设计。
1.1 除尘装置的工作原理及结构设计
除尘装置是通过链传动把动力输送到一组间隙可调节的上下排列的辊筒,通过上料平台将地毯由毯面朝下送入辊筒,在输送辊筒里间接排列四组齿型刮刷器,对毯面进行一定压力的刮刷,同时齿型刮刷器的下方安置一个广口的吸尘箱,把地毯上掉落的尘土、食物残渣、毛发等杂物收集起来。结构设计如图1所示。

图1 除尘装置结构设计
1.2 清洗装置的工作原理及结构设计
地毯毯面朝上通过带输送进入清洗装置[3],为了保证地毯清洗的质量[4],采用间歇式输送地毯前进的方式,当传感器[5]检测到地毯输送到旋转清洗头下方时,带输送停止工作,旋转清洗头和六分喷头在气缸带动下通过在X和Y两个方向上安装的齿轮齿条传输动力开始进行工作,能够保证在毯面上的自由移动,实现对毯面的全方位清洗。具体的地毯清洗过程类似于“扫地机器人”,通过对毯面预定运行轨迹[6]的设计,旋转清洗头以一定作用力对毯面预定区域进行旋转摩擦清洗。预定区域清洗完成后,带输送以地毯预定清洗区域的长度为一次输送距离,间歇式工作。结构设计如图2所示。

图2 洗涤装置结构设计
1.3 漂洗装置的工作原理及结构设计
经过清洗过程后毯面上残余大量的地毯清洗剂,漂洗装置是利用链传动将动力传递给动力滚筒,辊筒通过挤压将地毯经过导向板输送到漂洗槽进行漂洗作业。经过漂洗实验,洗涤过的地毯要经过三次漂洗才能将毯面上残留的地毯清洗剂彻底去除,为此漂洗装置要设计三道漂洗槽来依次漂洗地毯。同时,为了控制地毯清洗机的总体尺寸,本设计在漂洗装置第一道漂洗槽的内部套装了两道漂洗槽,使地毯能够在导向板的作用下依次经过三道漂洗槽进行漂洗工作,有效的节省空间。结构设计如图3所示。

图3 漂洗装置结构设计
1.4 脱水装置的工作原理及结构设计
脱水装置和除尘装置整体结构类似。地毯脱水将采用挤压脱水的方式,脱水装置是利用链传动把动力输送到一组间隙可调节的上下排列的辊筒,利用辊筒对地毯的挤压作用进行脱水处理,同时脱水机架下方安置一个回收水箱,可以把毯面脱离的水回收,该回收水箱储存的水可回收到洗涤水箱和漂洗槽中,可提高水的回收利用率。结构设计如图4所示。
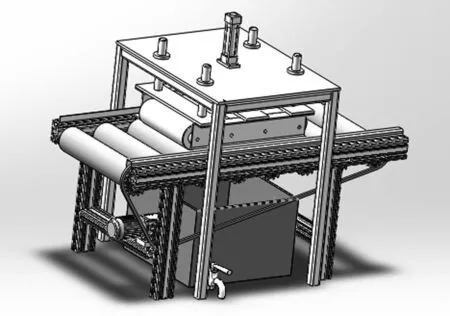
图4 脱水装置结构设计
1.5 地毯清洗机的整体结构设计
根据前面的地毯清洗方案设计,地毯清洗要依次经过除尘、清洗、漂洗和脱水处理。各清洗过程的装置都根据清洗要求和原理进行结构设计[7],地毯清洗机就是各部分功能集合的装置,整机的装配图如图5所示。
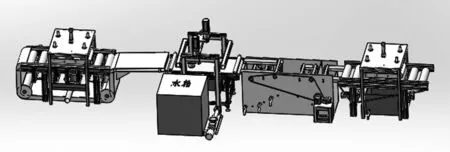
图5 地毯清洗机整机装配图
2 清洗机关键部位有限元仿真分析
对地毯清洗机的一些关键部位进行有限元分析[8],如除尘装置的机架及动力辊筒组、无动力辊筒组,清洗装置的齿轮齿条啮合部位进行强度验证,振型分析等。
2.1 地毯清洗机关键部位静力学仿真分析
2.1.1 静力学分析理论基础
静力学分析需要考虑如下假设条件:刚度系数矩阵[K]必须是常值,假设线弹性材料、采用小变形理论、可以采用部分非线性边界条件;{F}为静力载荷,不考虑随时间变化的载荷,不考虑惯性(如质量、阻尼)的影响。忽略通用运动方法与时间相关的选项,其方程式为:
[K]{μ}={F} (1)
2.1.2 机架及动力辊筒组静力学仿真结果分析
将模型导入ANASY workbench[9]中,设置材料属性为Structural steel;采用自动划分网格方法;因机架及动力辊筒组要承受来自于上方无动力辊筒组的压力和自身的重力,则给模型施加一个“Force”和标准地球重力。由于上下辊筒组之间通过四对辊筒相互作用,故在相互作用的每组辊筒接触面上都施加一个Force,大小为50 N;约束选择“Fixed Support”;右键单击“Solution”选择“Total Deformation”和“Equivalent Stress”求解;随后进入ANASY workbench的后处理求解过程,得到了该结构的总变形云图和等效应力云图,如图6和图7所示。

图6 机架及动力辊筒组总变形

图7 机架及动力辊筒组等效应力
从机架及动力辊筒组总变形云图可以看出:结构整体没有发生太大变形,最大变形位置发生在距离支撑柱最远的中间两辊筒处,变形量为2.9625E-3 mm。因变形量对于结构钢材质的机架及动力辊筒组相对较小,故符合刚度要求。
从机架及动力辊筒组等效应力云图可以看出:最大等效应力发生在处于中间处的辊筒与机架连接附近,为3.358 4 MPa,远小于材质为45钢的屈服强度355 MPa,故符合材料的强度要求。
2.1.3 无动力辊筒组静力学仿真结果分析
通过对该结构的静力学仿真分析,得到了无动力辊筒组的总变形云图和等效应力云图,如图8和图9所示。

图8 无动力辊筒组总变形

图9 无动力辊筒组等效应力
从无动力辊筒组的总变形云图可以看出:结构发生变形主要集中在模型的中间位置,呈中心对称状,由中间向四周变形呈现出同心圆的逐渐减小的变化规律,且最大变形位置发生在气缸整体和与气缸相接触的板面处,变形量为0.046 212 mm,符合刚度要求,在静载荷下可以正常工作。
从无动力辊筒组的等效应力云图可以看出:该结构的等效应力呈中心对称分布,最大应力发生在支撑架的内部四个角处、两侧横梁处,为9.217 3 MPa。则对结构施加的固定静载荷不会使其发生塑性变形,满足强度要求。
2.1.4 齿轮齿条啮合静力学仿真结果分析
通过对该结构的静力学仿真分析,得到了齿轮齿条啮合的总变形云图和等效应力云图,如图10-图13所示。

图13 齿轮齿条局部放大等效应力

图10 齿轮齿条总变形

图11 齿轮齿条局部放大总变形
从齿轮齿条总变形云图可以看出:变形主要发生在齿轮齿条啮合处和驱动电机的壳体部位,由齿轮齿条啮合处到电机壳体变形量逐渐向上积累变大,呈带状分布,最大变形发生在距离载荷施加处最大的电机顶部壳体处,为5.6132E-5 mm。这是因为,为了缩短求解时间,将该模型进一定的简化,使得电机缺少支撑,在离转速施加位置最大距离的电机壳体处产生最大变形。因变形量相对于金属材质的电机壳相对较小,不会影响齿轮齿条正常啮合的工况。

图12 齿轮齿条等效应力
从齿轮齿条等效应力云图可以看出:齿轮齿条的啮合基本处于正常应力范围,云图中的最大等效应力发生在齿轮齿条啮合的齿轮根部附近,为0.112 36 MPa,远小于齿轮材质为45钢的屈服强度355 MPa,故符合材料的强度要求。
2.2 地毯清洗机关键部位模态仿真分析
结构的受载还需要进行模态分析,得到正常工况下结构的固有频率和振型,以避免其运动频率接近固有频率而引起共振。
2.2.1 模态分析理论基础
动力学的通用方称为:
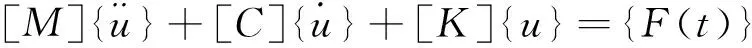
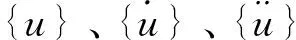
在实际的模态分析中,[C]一般可以忽略不计,F(t)=0,则在自由振动且忽略结构阻尼的情况下,式(2)可简化为:
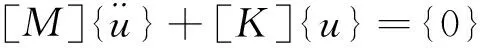
模态分析假定结构是线性的,因此[M]、[K]保持为常数,则自由振动为简谐运动:
{u}={φ}isin(ωi+θi) (4)
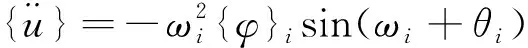


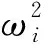
2.2.2 机架及动力辊筒组模态仿真结果分析
通过模态分析,得到了机架及动力辊筒的前六阶模态对应的总位移云图,如图14所示。
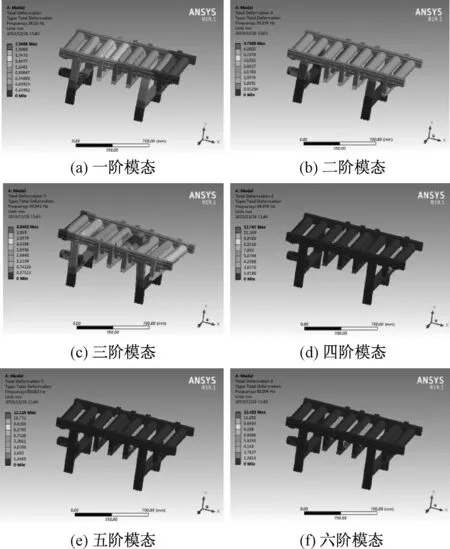
图14 机架及动力辊筒前六阶模态分析

2.2.3 无动力辊筒组模态仿真结果分析
通过模态分析,得到了无动力辊筒组的前六阶模态对应的总位移云图,如图15所示。

图15 无动力辊筒组前六阶模态分析
从无动力辊筒组的各阶云图可以看出:前两阶固有振型是沿Y轴的左右摆动;第三阶固有振型是绕Y轴的扭转;第四、五阶固有振型是沿Y轴正方向拉伸;第六阶固有振型是沿Y轴摆动。同时,整体的振动幅度较小,无动力辊筒组的一阶固有频率为18.724 Hz,远大于驱动电机的激振频率。因此在正常工作时,结构满足动态要求,不会发生共振。
2.2.4 齿轮齿条啮合模态仿真结果分析
通过模态分析,得到了无动力辊筒组的前六阶模态对应的总位移云图,如图16所示。

图16 齿轮齿条前六阶模态分析
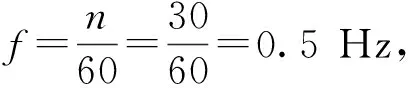
2.3 齿轮齿条瞬态动力学仿真分析
瞬态动力学分析是用来确定系统结构能否经受住随时间变化载荷作用的一种动态响应分析方法,来预测在随时变载荷作用下结构位移变形、应力和应变等。
2.3.1 瞬态动力学分析理论基础
瞬态动力学分析的控制方程是前面提到的动力学通用方程,运动方程的求解主要采用完全法和模态叠加法求解,本节主要讲解模态叠加法的求解理论。对于模态叠加法,可用模态坐标yi的线性组合来表示节点的位移{u},如下公式:
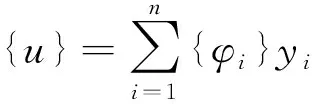
式中,{φi}表示第i阶模态的振型;n表示所提取的模态个数。把上式代入到动力学的通用方程中得:
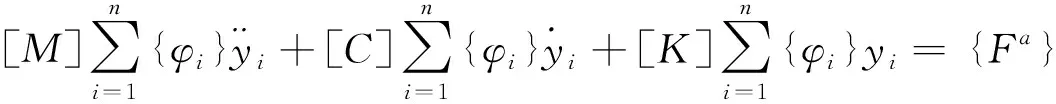
在上式中两边左乘一个经典的模态振型{φi}T,再将自然模态下的正交条件代入到上式中得:
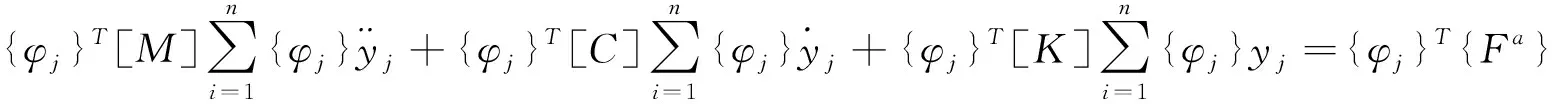
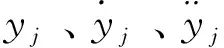
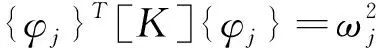

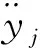
为了便于书写,可将简化为:
fj={φj}{Fa} (13)
把以上式子(10)到(13)代入式(10),得:

其中j表示任意一阶的模态,则上式代表n个未知数yj的解耦方程,其优点是,这种算法已经在模态计算中完成最费时间的计算,因此在大时间的瞬态动力学分析中效率较高。
2.3.2 齿轮齿条瞬态动力学仿真结果分析
通过瞬态动力学分析[10],得到了齿轮齿条啮合的总变形云图和等效应力云图,如图17和图18所示。

图17 齿轮齿条总变形

图18 齿轮齿条等效应力
从齿轮齿条总变形云图可以看出:在时变载荷的作用下,会发生一定的变形,驱动电机、传动轴以及齿轮均在Y轴方向上发生了一定的偏扭,最大变形发生在驱动电机壳体位置,为5.1227E-4 mm,符合材料的刚度要求,可正常工作。
从齿轮齿条等效应力云图可以看出:齿轮齿条受等效应力,主要集中在齿轮齿条将要退出啮合的作用部位,最大等效应力值的红色区域为1.033 4 MPa,远小于材料的屈服强度355 MPa,故齿轮齿条啮合工况符合材料的强度要求。
3 结论
1)根据飞机客舱地毯的清洗要求和原理,设计出一款结构体积小、操作方便、成本低的自动清洗机,来解决飞机客舱地毯清洗的压力,提高清洗的效率。
2)运用ANASY workbench软件对飞机客舱地毯清洗机进行仿真分析,能较好的模拟实际的受载情况,验证了清洗机的各部分结构设计符合强度刚度要求、满足动态要求。
