基于主成分分析法搭建A型星有效温度的神经网络模型*

李正泽，赵 刚

(1. 中国科学院光学天文重点实验室 (国家天文台)，北京 100101；2. 中国科学院大学天文与空间科学学院，北京 100049)

根据哈佛恒星光谱分类方法，恒星的光谱可分为O, B, A, F, G, K, M, R, S, N等光谱型，对应恒星的温度依次递减，A型星的温度区间位于7 500 K至11 000 K，呈白色，有强烈的氢吸收线，并且由于温度很高，同时具有电离钙和电离镁线[1-2]。于1993年提出建设的郭守敬望远镜[3]，2009年通过验收观测至今已经十余年，数据集DR5包括4 154个观测天区，发布901万条光谱，其中包含大量A型星的谱线指数和恒星参数。

相对于简单传统的回归模型，通过神经网络建立的回归模型可以更高效准确地完成任务，这要归功于神经网络模型可以捕捉非线性效应和更高阶的相互作用。对于较为复杂的数据和问题，神经网络可以挖掘数据背后的相关性，并且给出比较令人满意的结果，在数据处理领域，以神经网络为例的众多机器学习算法已经广泛应用于各个学科。

包括有效温度在内的恒星参数是决定恒星光谱的重要信息，对恒星演化的研究具有重要意义[4]。恒星参数的测量方法主要有两类[5]：(1)通过将待测恒星光谱与已知参数的标准恒星光谱进行匹配，将匹配最好的模板光谱参数作为待测恒星参数；(2)类似非线性回归的方法，比如神经网络模型，利用光谱数据通过神经网络结构训练测试恒星大气参数[5]。谱线指数是包含恒星自身物理特征信息的重要参数，利用谱线指数可以进行众多的天文研究，例如：文[6]利用谱线指数对恒星光谱进行聚类分析研究。文[7]利用谱线指数建立人工神经网络对包括有效温度在内的恒星参数进行了测量，文中使用LAMOST数据训练得到的模型，预测得到有效温度的误差正态分布数学期望为-316.02，标准差为617.36。使用SDSS DR8数据训练的模型结果稍好，但误差的正态分布数学期望为88.58，标准差为147.81。可见文中的方法还不能比较准确地给出有效温度，需要进一步研究改进。

本文使用主成分分析方法(Principal Components Analysis, PCA)，运用于DR5数据集中的A型星数据，对19种谱线指数进行相关性降维，再给出每种谱线指数占整个数据信息的百分比，以此为依据，选择与有效温度关系最紧密的几种谱线指数作为模型的输入，经过测试，选择占比最大的前12种谱线指数作为神经网络模型的输入。同时选择有效温度误差小于100 K的数据作为输入数据，训练得到了A型星的谱线指数与有效温度的神经网络回归模型。通过建立的神经网络模型，给出了8 644组有效温度误差大于100 K的A型星有效温度，一定程度上对数据进行了改进与提升，并且通过神经网络模型对DR5数据集中光谱型为A5，缺少有效温度的恒星光谱进行了补充，给出了这些恒星的有效温度。

1 主成分分析

如今科学研究面临的问题日渐深入复杂，要处理的数据量也随之剧增，单纯直接处理庞大的数据已经不能满足科学研究对高效性的追求。为了从复杂繁琐的数据中提取主要信息，必须利用一些科学手段，寻找数据之间的相关性，对数据进行简化，有效减少数据的维度，但同时保证数据提供的信息极大程度地保留下来，尽量减少在这个过程中数据所携带信息的损失。主成分分析法便是这样一种算法，现在已经成为使用最广泛的降维方法之一。

主成分分析法是一种运用十分广泛的降维方法。对于大样本多参量观测数据, 它可以简捷有效地寻求参量之间的相互关系，从而实现对数据降维，可以去除数据噪声，消除数据沉余，使得数据更易使用。主成分分析法的主要思想是找出数据最主要的信息、最主要的成分代替原始数据，以此达到对原始数据降维的目的，即在减少需要分析的指标的同时，尽量降低原指标所包含信息的损失。这种方法最早被应用于社会科学研究领域。之后随着20世纪60年代计算机的兴起和发展，开始广泛应用于自然科学研究领域[8]，与此同时，主成分分析法也开始应用于天体物理学领域，在近几年的天文研究中，文[9]利用LAMOST巡天光谱DR2数据，使用R语言的主成分分析工具提取各类型光谱数据的特征量，从含有大量冗余信息的光谱中提取代表恒星光谱特征的主要成分。除此之外在星系和恒星的光谱分类[2]、特征参量的挑选、活动星系核光变的研究、大样本天体红移的测量等方面，主成分分析法都有不错的表现[8]。近年来随着计算机与机器学习的飞速发展，为了克服主成分分析法的一些缺点，开发了很多主成分分析法的一些变种，比如解决非线性降维的核主成分分析(Kernel PCA, KPCA)，解决内存限制的增量主成分分析(Incremental PCA)，以及解决稀疏数据降维的稀疏主成分分析(Sparse PCA)等。

1.1 主成分分析的数学原理

首先假设需要处理分析的数据样本由n个天体组成，每个天体对应m个观测参量，即m个特征指标，因此，观测量可以表示成矩阵X，如(1)式，矩阵X称之为观测矩阵，其行矢量对应同一天体的不同特征量，列矢量对应不同天体的同一特征量。

(1)

设待求的m维特征向量为e，则一个主成分pc可以表示为

pc=eX=e1xk1+…+eixki+…+emxkm.

(2)

同时，为了保证在降维过程中数据携带的信息不丢失，降维后的主成分应尽可能多地体现原始观测数据的信息，并且保证主成分之间互相独立。随机变量的方差可以体现随机变量所携带的信息，而不同的特征向量e，其方差的大小也不同，主成分分析法就是寻找使主成分pc的方差达到最大的一组特征向量e。为此，根据最小二乘法原理，此处的e为观测矩阵X的协方差矩阵C=(cjk)m×m的正交特征矢量，其中cjk的表达式为

(3)

(4)

构造行列式方程|C-lI|=0，其中l为行列式的特征根，I为m×m的单位矩阵，通过求解这个方程，可以得到特征根l，再求解：

(C-lI)ei=0 ，

(5)

就能求得特征矢量ei。

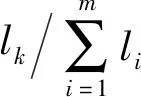
1.2 主成分分析的算法流程

(1)对样本中每个特征指标下的数据，减去该特征的平均值，即对所有样本进行中心化；

(2)计算样本矩阵的协方差矩阵；

(3)求协方差矩阵的特征根和特征根所对应的特征矢量；

(4)根据特征根的大小，计算得到每个特征根对应的贡献率和累计贡献率；

(5)用每一个特征矢量乘以样本矩阵计算得到每一个主成分，即降维后输出的新样本。

1.3 主成分分析结果

利用DR5数据集给出的谱线指数、有效温度以及有效温度误差，给定温度为7 500 K至11 000 K提取A型星的数据，之后首先对数据筛选预处理，去除一些明显异常的数据，比如空值、显示为-9 999的数据，除此之外，正常情况下谱线指数都应该是正值，但是由于郭守敬望远镜流量定标没有定好，有些谱线指数的数据出现负值，因此，这里只选取谱线指数为正值的正常数据，一共选取53 739组A型星的数据。

通过主成分分析方法对19种谱线指数数据(kp12, kp18, kp6, hdelta12, hdelta24, hdelta48, hdelta64, hgamma12, hgamma24, hgamma48, hgamma54, hbeta12, hbeta24, hbeta48, hbeta60, halpha12, halpha24, halpha48, halpha70)进行相关性降维，设定累计贡献率大于90%，得到了3个主成分，方差分别为15.479, 1.563, 1.507。因此，主成分一的贡献率α=77.82%，主成分二的贡献率β=7.86%，主成分三的贡献率γ=7.58%。再结合主成分分析过程中得到的转换矩阵w：

(6)

(7)

(8)

表1 每种谱线指数占整个数据信息的百分比大小Table 1 The percentage of the entire information for each spectral index

2 搭建神经网络模型

本文使用的机器学习模型是多层感知器(Multilayer Perceptron, MLP)，即神经网络模型[10-11]，在Python环境下提供了多种机器学习算法，其中sklearn.neural_network模块提供多层感知器回归算法，即MLPRegressor[12]。多层感知器顾名思义，由多个层构成，包括一个输入层和可以规定数量的多个隐藏层以及一个输出层，隐藏层的加入增强了模型的表达能力，但同时也使模型变得更加复杂，对于输出层的神经元来说，可以有不止一个输出。

神经网络模型设置了两个隐藏层，每个隐藏层包含100个节点，多层感知器回归算法可选择的激励函数有4种，分别是identity，logistic，tanh，relu，分别测试这4种激励函数下模型的表现，如表2。由表2可以看出，选择identity和relu时模型表现比较好。选择relu时模型表现更好，并且选择relu时模型训练速度较快，效率较高。因此，搭建神经网络模型的激励函数设置为relu。但是选择relu作为激励函数时有一个缺点，可能会造成神经元坏死，为了避免这种情况，这里网络的学习速率设置得较小，避免权重突然更新过多导致神经元彻底关闭。

表2 不同激励函数下多层感知器的表现Table 2 The performance of MLP by using different Activation function

经过测试，梯度下降函数选择在较大数据集上效果较好的adam，此时模型运算效率较高并且结果较好。设置正则化系数alpha是为了避免过拟合，设置为0.001，同时保证模型的运行结果较好。最大训练迭代次数max_iter经过测试设置为4 000。除此之外其他参数为默认值。

2.1 选择输入参数

图1是郭守敬望远镜提供的有效温度的绝对误差分布，选取有效温度误差小于100 K，共计45 095组数据建立模型，其中随机选取80%的数据作为训练数据，20%的数据作为训练之后的测试数据。通过主成分分析法给出了19种谱线指数占整个数据信息的百分比大小排序，据此，选择与有效温度关系最紧密的几种谱线指数作为神经网络模型的输入，按照信息占比从大到小依次选择1种到全部19种谱线指数作为神经网络模型输入。测试不同指标数量下模型的表现，建立模型之后score命令可以给出模型的评分，即模型对全部数据的预测结果的决定系数R2：

图1 有效温度绝对误差分布图

(9)

表3与图2是以模型的评分为标准给出的结果。可以看出，选取包含信息最多的前12种谱线指数时，模型的评分最高，模型表现最好，因此，选取前12种谱线指数，即hgamma54, hdelta64, hgamma48, hdelta48, halpha70, hbeta60, halpha48, hbeta48, kp18, hdelta24, hgamma24, kp12作为神经网络模型的输入。

表3 不同指标数量下模型的评分Table 3 The model score for different number of features

图2 模型评分随指标数量的变化

2.2 建立模型

2.2.1 模型在训练数据集上的表现

在80%的训练数据集上，用得到的神经网络模型对有效温度进行了预测，如图3(a)，训练数据集36 076个数据点整体分布在相对集中的区域，个别数据偏离较大，除此之外，由图3(b)可以看出，随着有效温度升高，误差存在一个轻微的下降趋势，文[7]对这种现象的解释是可能因为人工神经网络内部的机制，考虑到数据本身对于早型星的恒星参数测量并不准确，所以有可能是数据本身的影响造成的，有待进行更加深入的讨论。经过计算绝对误差的平均值为58.12 K，标准差为60.99 K，结合测试数据集的预测结果，两者的平均绝对误差和标准差的结果基本一致，由此可以表明，神经网络模型并没有发生过拟合。

图3 神经网络回归模型在训练数据集上的预测结果Fig.3 The results of forecast by neural network on train data set

图4给出了误差分布及其拟合的正态分布曲线，正态分布的数学期望为-3.668，标准差为84.167。图5是神经网络模型的学习曲线，从图中可以看出，随着训练样本数量的增加，训练得分(图中红线部分)快速增加，达到饱和之后趋于水平。测试得分(图中绿线部分)与训练得分变化趋势一致，但是并没有出现训练得分较高、测试得分较低或者测试得分达到某一值后迅速下降，即过拟合的情况。除此之外，训练得分与测试得分都处于较高的水平，因此，神经网络模型并没有欠拟合。整体来看，模型的学习曲线收敛且误差较小，是一条比较理想的学习曲线。

图4 训练数据集有效温度的误差分布图Fig.4 Error distribution diagram of effective temperature on train data set

图5 神经网络学习曲线Fig.5 Learning curves

2.2.2 模型在测试数据集上的表现

对于神经网络回归模型，程序给出的评分为0.904，图6是在测试数据集上得到的有效温度的预测结果，其中，由图6(a)可以看出，预测有效温度与实际有效温度成正比，整体预测结果较好，绝对误差的平均值为58.38 K，不足A型星有效温度的1%，标准差为60.81 K，但是还是存在个别预测数据与实际数据偏离较大。图6(b)给出了模型的误差变化趋势，可以看出，误差围绕在纵坐标轴y=0上下，个别数据出现了较大的偏离，除此之外，还能够看出误差有一个轻微的下降趋势。图6(c)给出了误差的分布及其拟合的正态分布曲线，可以看出与训练数据集上的结果一致，误差主要集中在100 K以内，正态分布拟合的数学期望为-3.366，标准差为84.229。可见模型的有效温度预测准确度相比文[7]建立的模型有了很大的改进与提升。

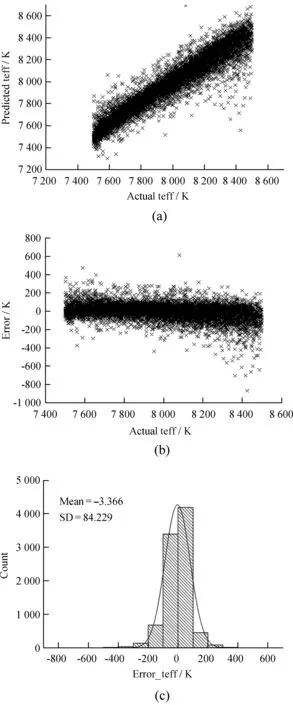
图6 神经网络回归模型在测试数据集上的预测结果

2.3 不同模型比较

支持向量机和神经网络模型都可以解决非线性的回归问题，通过sklearn.svm中的SVR模块，建立了一个支持向量机回归模型(Support Vector Regression, SVR)与前文的神经网络模型进行了对比，见表4。此外还建立了一个决策树回归模型(Decision Tree Regression, DTR)，选取80%的数据作为训练数据，20%的数据作为测试数据，为了防止严重过拟合，经过测试，决策树回归模型的最大深度设置为6。查看决策树回归模型在两个数据集上的结果，此时在训练数据集上绝对误差的平均值为65.10 K，标准差为61.74 K，在测试数据集上绝对误差的平均值为66.76 K，标准差为62.83 K，因此，模型没有发生过拟合。表4给出了3种模型在测试数据集上的结果对比。可以看出，神经网络模型在评分和误差方面比支持向量机、决策树回归模型有更好的结果。图7(a)和图7(b)分别给出了支持向量机和决策树回归模型在测试数据集上的误差变化，前文提到神经网络模型随着有效温度的变大，误差存在一个轻微的下降趋势，从图7(a)支持向量机模型整体来看，误差也存在一个下降的趋势，尤其是8 200 K到8 500 K之间，误差有明显的下降趋势，因此，产生这个现象的原因可能不单单是神经网络内部的原因，也可能与数据本身有关。

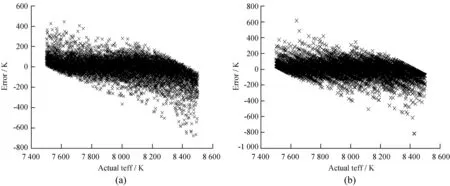
图7 支持向量机和决策树回归模型在测试数据集上的预测结果Fig.7 The results of forecast by SVR and DTR

表4 模型的比较Table 4 The comparison of different models

3 神经网络模型的应用

3.1 对有效温度误差较大的数据进行改进

选取了DR5数据集中包含有效温度、有效温度绝对误差以及19种谱线指数的A型星数据，共计53 739组，使用其中有效温度误差小于100 K共45 095组数据建立了神经网络模型。通过建立的神经网络模型对有效温度误差大于100 K的8 644组数据，使用其谱线指数进行了计算预测，给出了有效温度值，对数据进行了改进与提升，具有一定的参考价值。对于DR5数据集中有效温度绝对误差大于100 K的数据，图 8(a)是有效温度绝对误差的分布图，图8(b)是通过模型的预测得到的有效温度的绝对误差分布图。对于郭守敬望远镜给出的有效温度绝对误差平均值为185.10 K，标准差为78.79 K；神经网络模型给出的有效温度绝对误差平均值为115.24 K，标准差为104.88 K。可以看出，有效温度绝对误差平均值有明显下降，对于有效温度在一定程度上有所改进。

图8 有效温度绝对误差与模型预测得到的有效温度绝对误差分布图Fig.8 Absolute error distribution diagram of effective temperature for LAMOST and prediction

3.2 对郭守敬望远镜缺少的A5光谱型恒星有效温度数据的补充

DR5数据集一共给出了40多万条A型星光谱，但明确给出有效温度的A型星只有8万多颗，这其中还包括很多误差非常大的数据。对于有效温度的测量，通过神经网络模型可以使用谱线指数更加自动高效地进行测量，一定程度上弥补这部分数据的缺失。依据哈佛天文台的恒星光谱分类系统，除了分为O, B, A, F, G, K, M, R, S, N几个光谱型之外，对于每种光谱型还可以分为10个次型，用数字0到9表示，并且对应恒星的温度依次下降[2]。考虑到模型使用有效温度7 500 K到8 500 K的数据训练建立的，这里选取温度区间相近的光谱型恒星，以A5型恒星数据为例[2]，郭守敬望远镜提供的谱线指数分类为A5型的恒星一共有470组，大多没有给出有效温度。考虑到流量定标没有定好，导致谱线指数出现负值的情况，选取其中每种谱线指数都大于0的数据，通过神经网络模型给出了这些恒星的有效温度，表5展示了其中一小部分结果，包括观测号(obsid)、赤纬(Dec)、赤经(Ra)和预测得到的有效温度(teff)。根据MK分类系统的光谱型与有效温度之间的关系[2]，对于A5型恒星来说，光度级为I(超巨星)，即A5 I型恒星的有效温度为8 610 K；光度级为V(主序星)，即A5 V型恒星的有效温度为8 180 K，光度级VI(亚矮星)型恒星的有效温度更低。考虑到观测数据的分类以及谱线指数都可能不准确，预测得到的A5型恒星的有效温度基本符合上述范围。

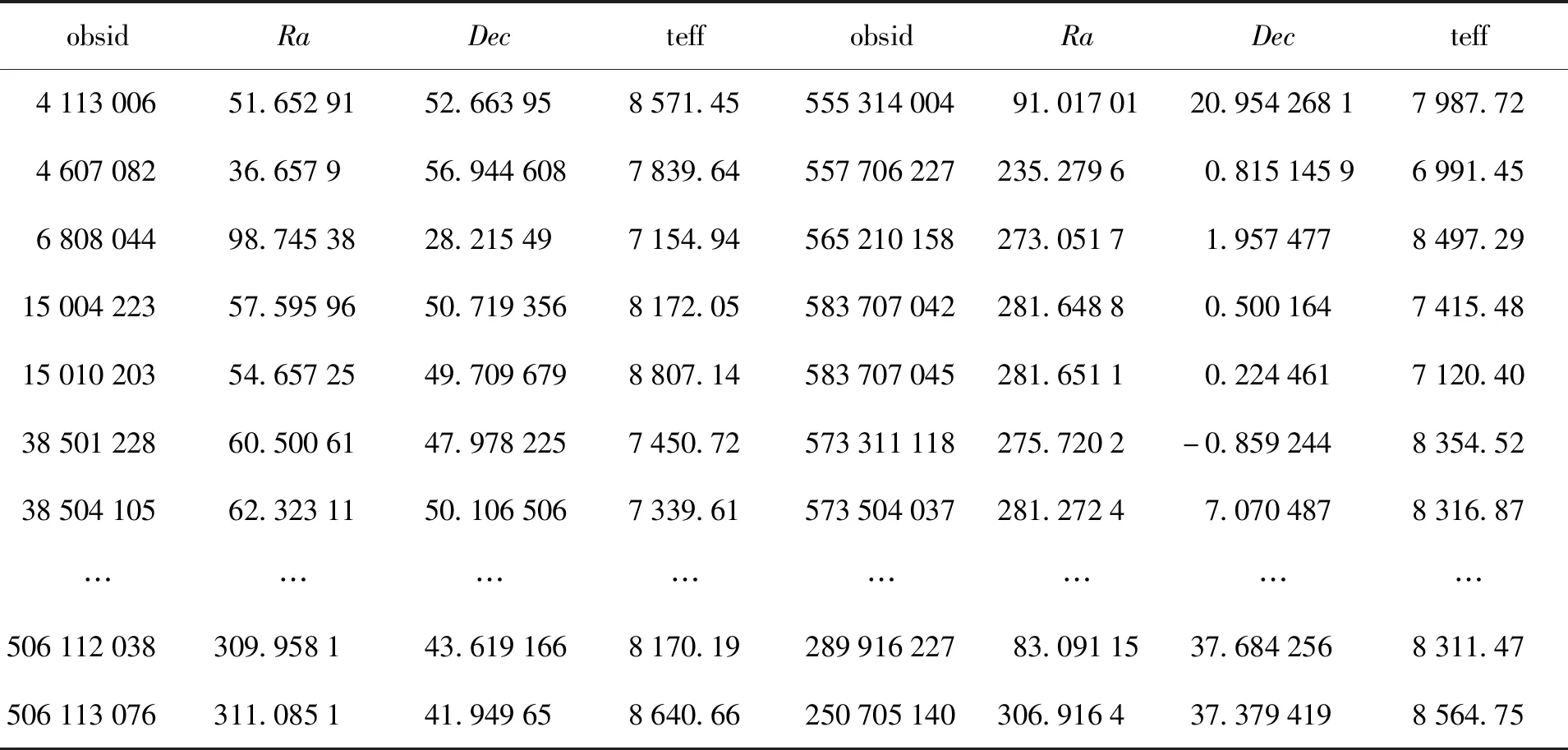
表5 预测得到DR5数据集中A5型恒星的有效温度Table 5 Predicted effective temperature of A5 type star in LAMOST DR5 data set

4 结 论

通过DR5数据集提供的A型星19种谱线指数与有效温度，通过主成分分析法进行相关性降维，根据每种谱线指数占整个数据信息的百分比，经过测试选择与有效温度关系最紧密的12种谱线指数作为输入数据。筛选有效温度误差小于100 K的数据建立了神经网络回归模型，模型在测试数据集上表现良好，评分为0.904，平均绝对误差为58.38 K，标准差为60.81 K。对比相关研究的模型，准确度有了很大的提升。通过有效温度神经网络回归模型对有效温度误差大于100 K的数据进行了预测，经过模型预测得到的有效温度的绝对误差平均值有明显的下降，一定程度上对这部分数据进行了改进与提升，此外，DR5数据集提供了大量的A型星数据，但绝大部分缺少有效温度，通过神经网络模型可以实现高效自动较为准确地给出这部分数据，以光谱型为A5的恒星数据为例，对缺少有效温度的A型星数据进行了补充。

包括A型星在内的早型星的恒星参数不容易测量得到，郭守敬望远镜巡天项目提供了海量的光谱观测数据,其中包括大量的A型星数据，但包括有效温度在内的恒星参数却非常缺乏。通过本文方法验证了建立神经网络模型利用谱线指数预测有效温度的方法是有效可行的，同时该方法能够自动高效地测量有效温度，并且测量的准确度相比于前人建立的模型有了很大的提升。