预报模型及建模序列长度对钟差短期预报精度影响研究*

郭忠臣，孙 朋，李致春，白洪伟

(宿州学院环境与测绘工程学院，安徽 宿州 234000)

卫星钟差(Satellite Clock Bias, SCB)是全球卫星导航系统(Global Navigation Satellite System, GNSS)实现高精度定位、导航和授时的重要参数之一，但国际GNSS服务(International GNSS Service, IGS)发布的精密钟差产品会有一定程度的延迟[1-2]，为实现用户实时、高精度的使用要求，对卫星钟差的预报进行研究就成为当前的重要任务之一。

用于卫星钟差预报的模型主要有二次多项式模型[3]、灰色模型[4-5]、自回归滑动平均(Autoregressive Moving Average, ARMA)模型[6]、卡尔曼(Kalman)滤波[7]和人工神经网络模型[8-9]等，不同模型在预报时均有各自的优势和局限性[8]。由于全球定位系统星载原子钟的类型不完全相同，其特性及稳定性也有所不同，故其适用的预报模型也不一定相同[10]。不少学者对钟差进行预报时，主要是验证模型的预报精度，并没有对不同类型原子钟更适合哪种模型进行分析。另外，在研究预报模型的过程中，多是选取固定长度的原始钟差序列进行预报，鲜有考虑采用不同长度的原始钟差序列建模对预报精度的影响，且多数实验选择变化趋势较为稳定的卫星钟差数据，也没有对钟差具有一定波动情况下不同模型的预报精度进行分析。

本文选取灰色模型、灰色 + 自回归模型和二次多项式模型对全球定位系统卫星钟差的短期预报进行研究，首先，分析采取不同预报模型时，不同类型原子钟的预报精度；其次，对不同类型原子钟预报时，选取不同长度的钟差序列进行建模，研究不同卫星在不同模型下的最佳建模长度；最后，选取钟差序列波动的时间段进行预报，分析钟差序列波动大小对不同模型预报精度的影响。

1 预报模型

1.1 二次多项式模型

Xi=a0+a1(ti-t0)+a2(ti-t0)2+ε，

(1)

其中，i=1,2,…,n；t0为参考时刻；ti为历元时刻；a0，a1和a2分别为t0时刻的钟差、钟速和钟漂；ε为误差。当原始钟差序列长度n大于3时，即可根据最小二乘原理解算参数。

1.2 灰色模型

对X(1)建立微分方程((3)式)，即可根据最小二乘原理求得参数。

(2)

其中，a为模型的发展系数；b为灰色作用量。

依据(2)式的响应函数，可得X(1)的预报模型为

(3)

其中，k为参与建模的原始数据个数，对预报的x(1)(k)序列依次执行累减即可得到原始序列的预测结果。

1.3 自回归模型

Xn=α1Xn-1+α2Xn-2+…+αpXn-p+εn，

(4)

其中，αi为模型系数；p为模型阶数；εn为白噪声。

自回归模型阶数通常由赤池信息准则(Akaike Information Criterion, AIC)和贝叶斯信息准则(Bayesian Information Criterion, BIC)确定，之后根据最小二乘法解算模型系数。本文采用贝叶斯信息准则确定模型最佳阶数，贝叶斯信息准则定义如下[12]：

BIC(p)=plnn-2lnL，

(5)

其中，p为模型阶数；n为样本量；L为似然函数。

2 实验分析

为分析不同因素对钟差预报精度的影响，本文选取IGS发布的2016年10月01日至10月31日共31天的精密钟差产品作为实验数据，采样间隔为5 min。考虑到全球定位系统星载原子钟有不同类型[12]，主要选取具有代表性的PRN02(IIR RB)，PRN06(IIF RB)，PRN08(IIF CS)和PRN29(IIR-M RB)进行实验，采用二次多项式模型、灰色模型和灰色 + 自回归模型3种预报算法分别进行预报，以研究原子钟类型、原始钟差序列长度及其波动情况对预报精度的影响，采用最大值(MAX)、最小值(MIN)、平均值(MEAN)和均方根误差(RMS)对预报结果的精度进行统计。

2.1 不同类型原子钟预报精度分析

全球定位系统星载原子钟种类不同，为分析不同类型原子钟的预报精度，分别以前一天的钟差(24 h，288个历元)作为原始钟差序列建模，预报接下来时长为6 h，12 h和24 h的钟差，如采用10月01日24 h的钟差数据建模对10月02日前6 h，12 h和24 h的钟差进行预报，重复预报30次，并对30次预报结果进行统计分析。由于搭载铯钟的卫星较少，除上述4颗卫星外，增加PRN24(IIF CS)一同进行实验。由于篇幅问题，文中只给出了5颗卫星24 h的钟差预报结果，见图1至图5，表1给出了5颗卫星不同情况下的预报精度统计。

表1 3种模型预报不同时长的精度统计(单位：ns)Table 1 Accuracy statistics of three models with different prediction time length (unit: ns)

图1 PRN02 24 h预报误差Fig.1 24 h prediction errors of PRN02

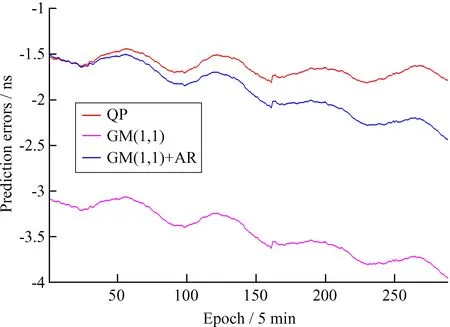
图2 PRN06 24 h预报误差Fig.2 24 h prediction errors of PRN06

图3 PRN08 24 h预报误差Fig.3 24 h prediction errors of PRN08

图4 PRN24 24 h预报误差Fig.4 24 h prediction errors of PRN24

图5 PRN29 24 h预报误差Fig.5 24 h prediction errors of PRN29

通过分析可知：

(1)从3种算法预报误差的波动情况看，铷钟(PRN02, PRN06, PRN29)误差波动幅度均在3 ns以内，部分情况的波动误差在1 ns，3种算法的预报误差波动幅度类似，主要由于铷钟较为稳定；铯钟(PRN08, PRN24)的预报误差波动幅度受算法影响较大，二次多项式模型的预报误差波动明显较大，可达12 ns，灰色模型和灰色 + 自回归模型的预报误差波动幅度可控制在3 ns。另外对3种算法预报结果的平均值和均方根误差对比，也说明灰色模型和灰色 + 自回归模型对于铯钟的预报相对二次多项式模型更稳定。

(2)铯钟虽然稳定性低于铷钟，但从预报结果的平均值和均方根误差可知，铯钟采用灰色模型和灰色 + 自回归模型的预报精度可与铷钟相当甚至部分情况下优于铷钟，这也从侧面说明了灰色模型的抗干扰能力较强，而二次多项式模型预报铯钟的误差较大，说明二次多项式模型更适合对变化趋势较为稳定的钟差进行预报。

(3)对比不同卫星的预报结果，总体来说，当原始序列长度为24 h时，采用灰色 + 自回归模型的预报效果最好，这是因为组合模型从一定程度上继承了单一灰色模型的优点且降低了灰色模型的预报风险，而自回归模型对灰色模型的拟合残差进行预报，也起到对灰色模型修正的作用，实现优势互补。

2.2 原始钟差序列长度对建模预报结果的影响

不同模型在预报时，模型参数主要依据最小二乘原理解算，因此，建模序列的长度对模型参数的计算会产生一定的影响，不同的模型参数也会导致模型的预报结果有所差别。为分析建模序列长度对钟差预报精度的影响，分别以前一天2～24 h的钟差序列构建二次多项式模型、灰色模型和灰色 + 自回归模型对PRN02，PRN06，PRN08和PRN29 4颗卫星接下来24 h的钟差进行预报，重复预报30次，并以平均值和均方根误差作为精度评价指标。各卫星采用不同长度钟差序列预报的结果统计见图6～图9。

图6 PRN02不同长度钟差序列建模预报精度统计Fig.6 Prediction accuracy statistics of different length modeling series of PRN02

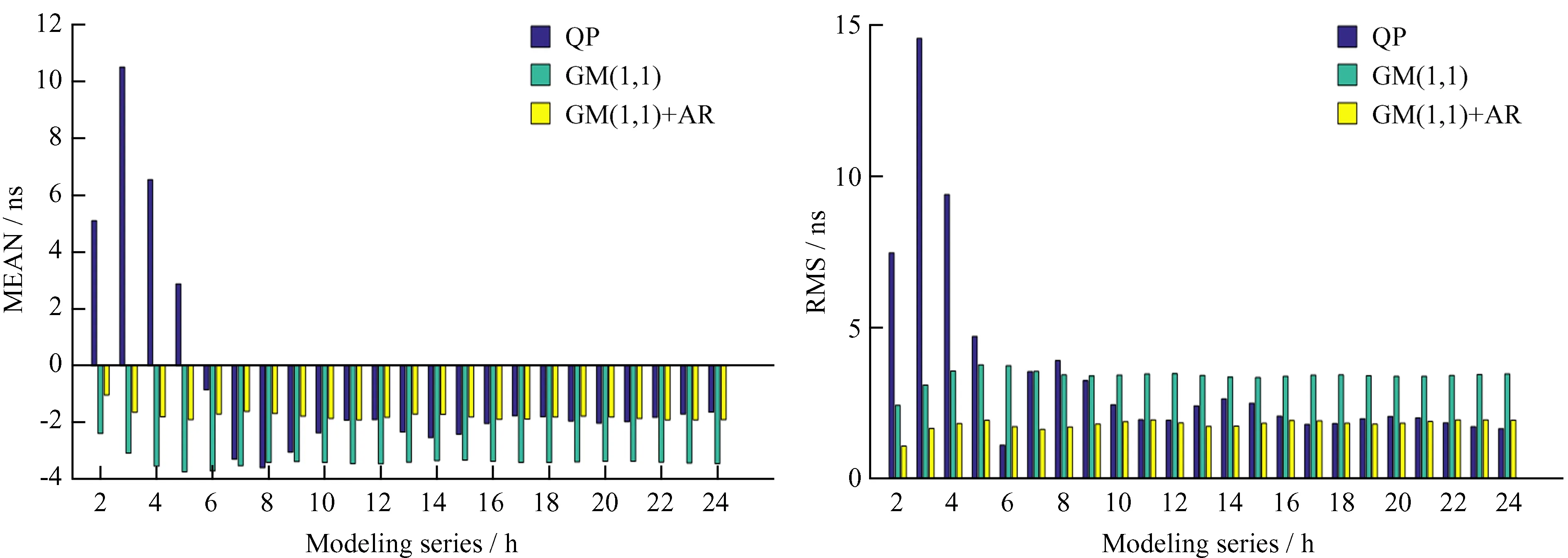
图7 PRN06不同长度钟差序列建模预报精度统计Fig.7 Prediction accuracy statistics of different length modeling series of PRN06

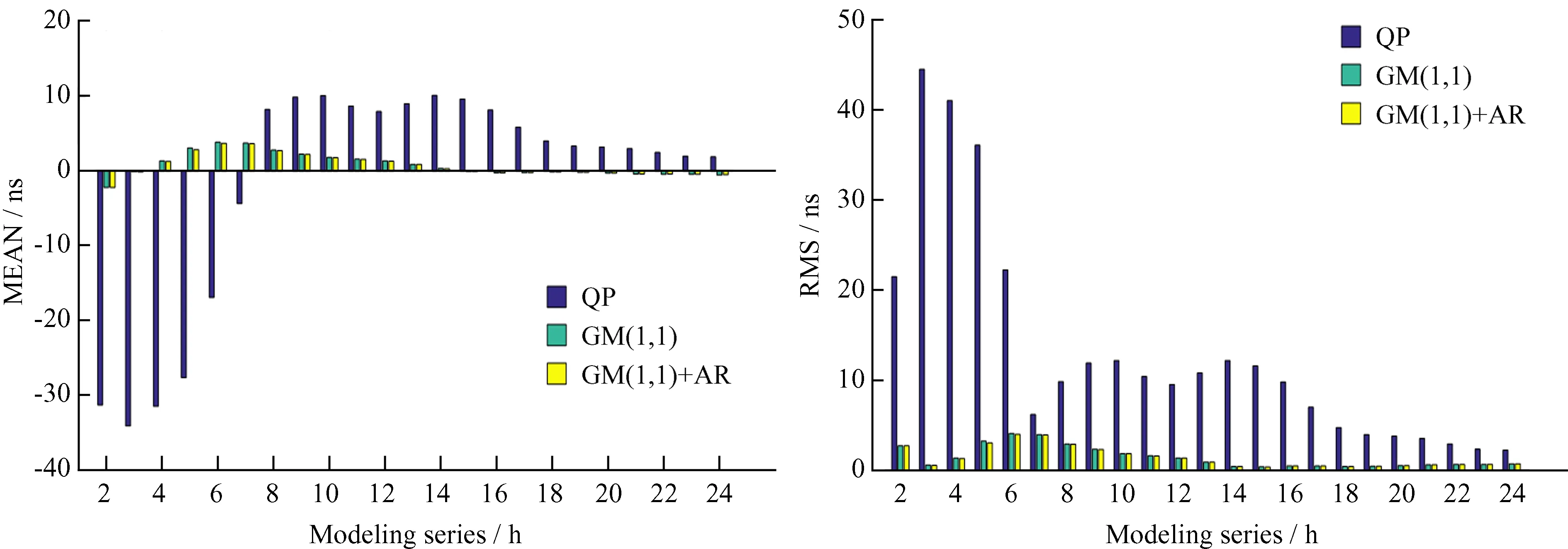
图8 PRN08不同长度钟差序列建模预报精度统计Fig.8 Prediction accuracy statistics of different length modeling series of PRN08

图9 PRN29不同长度钟差序列建模预报精度统计Fig.9 Prediction accuracy statistics of different length modeling series of PRN29

对预报结果统计分析可知：

(1)不同模型的预报精度与原始建模序列有一定关系，其中二次多项式模型受影响最大，当建模序列较短时，预报误差较大，随着建模序列增长，预报误差逐渐变小；灰色模型和灰色 + 自回归模型受建模序列长度的影响相对较小，模型抗干扰能力强，预报结果较为稳定，这也说明灰色模型在数据量较少的情况下建模效果比较好，但灰色 + 自回归模型的预报效果优于灰色模型。以PRN02为例，当建模序列长度为2 h时，二次多项式模型和灰色 + 自回归模型预报误差统计的平均值和均方根误差分别是7.235 ns，0.775 ns和8.743 ns，0.974 ns，当建模序列长度为24 h时，二次多项式模型和灰色 + 自回归模型预报误差统计的平均值和均方根误差分别是1.821 ns，1.093 ns和1.823 ns，1.160 ns，与2 h的建模序列预报结果相比，二次多项式模型的预报精度提高了79.15%，灰色 + 自回归模型的预报精度降低了19.10%。另外，对于2 h和24 h的钟差序列建模预报结果，灰色 + 自回归模型的精度较二次多项式模型分别提高了88.86%和36.37%，说明二次多项式模型适合原始数据量较多时的建模预报，而灰色 + 自回归模型受原始建模序列长度的影响较小，预报效果较为稳定。

(2)不同卫星预报24 h的最佳建模序列长度因使用模型的不同而不同。对二次多项式模型的预报结果分析可知，PRN02在序列长度为4 h时的预报效果最佳，而PRN06，PRN08和PRN29的最佳序列长度分别为6 h，24 h和22 h；对于灰色模型，PRN02，PRN06，PRN08和PRN29的最佳序列长度分别为4 h，2 h，15 h和24 h；对于灰色+自回归模型，PRN02，PRN06，PRN08和PRN29的最佳序列长度分别为2 h，2 h，15 h和24 h。

(3)铷钟受建模序列长度的影响总体上小于铯钟，当原始钟差序列长度增加到一定程度时，铷钟和铯钟的钟差预报精度会逐渐趋于稳定。

2.3 原始钟差序列波动对预报结果的影响

通过卫星钟差的趋势变化情况可知，卫星钟差具有缓慢下降或者上升的趋势，但部分卫星的钟差也会在一些时段内波动较大。对2016年10月24日的钟差数据波动情况分析可知，PRN12(IIR-M RB)和PRN21(IIR RB)的钟差序列存在波动情况，且PRN12的波动幅度明显大于PRN21，两颗卫星的钟差序列见图10，为研究原始钟差序列波动对预报结果的影响，将其与钟差序列平稳变化时间段的预报情况进行对比。通过对2016年10月24日附近时间段内IGS发布的PRN12和PRN21的钟差产品比较，发现2016年6月27日的钟差序列波动较为平稳(见图11)，分别采用二次多项式模型、灰色模型和灰色 + 自回归模型对10月24日和6月27日后一天的PRN12和PRN21的钟差进行预报，为便于对比，预报均以24 h的钟差序列建模，图12和图13给出了两种情况在不同模型下的预报误差，PRN121和PRN211表示钟差序列具有一定波动，PRN122和PRN212表示钟差序列变化趋势较为平稳，图中从上到下分别为二次多项式模型、灰色模型和灰色 + 自回归模型的预报误差，表2给出了两种情况的预报误差统计。

图10 PRN12和PRN21钟差序列(2016年10月24日)Fig.10 Satellite clock bias of PRN12 and PRN21 (October 24, 2016)

图11 PRN12和PRN21钟差序列(2016年6月27日)Fig.11 Satellite clock bias of PRN12 and PRN21 (June 27, 2016)

图12 PRN12预报误差对比Fig.12 Prediction errors comparison of PRN12

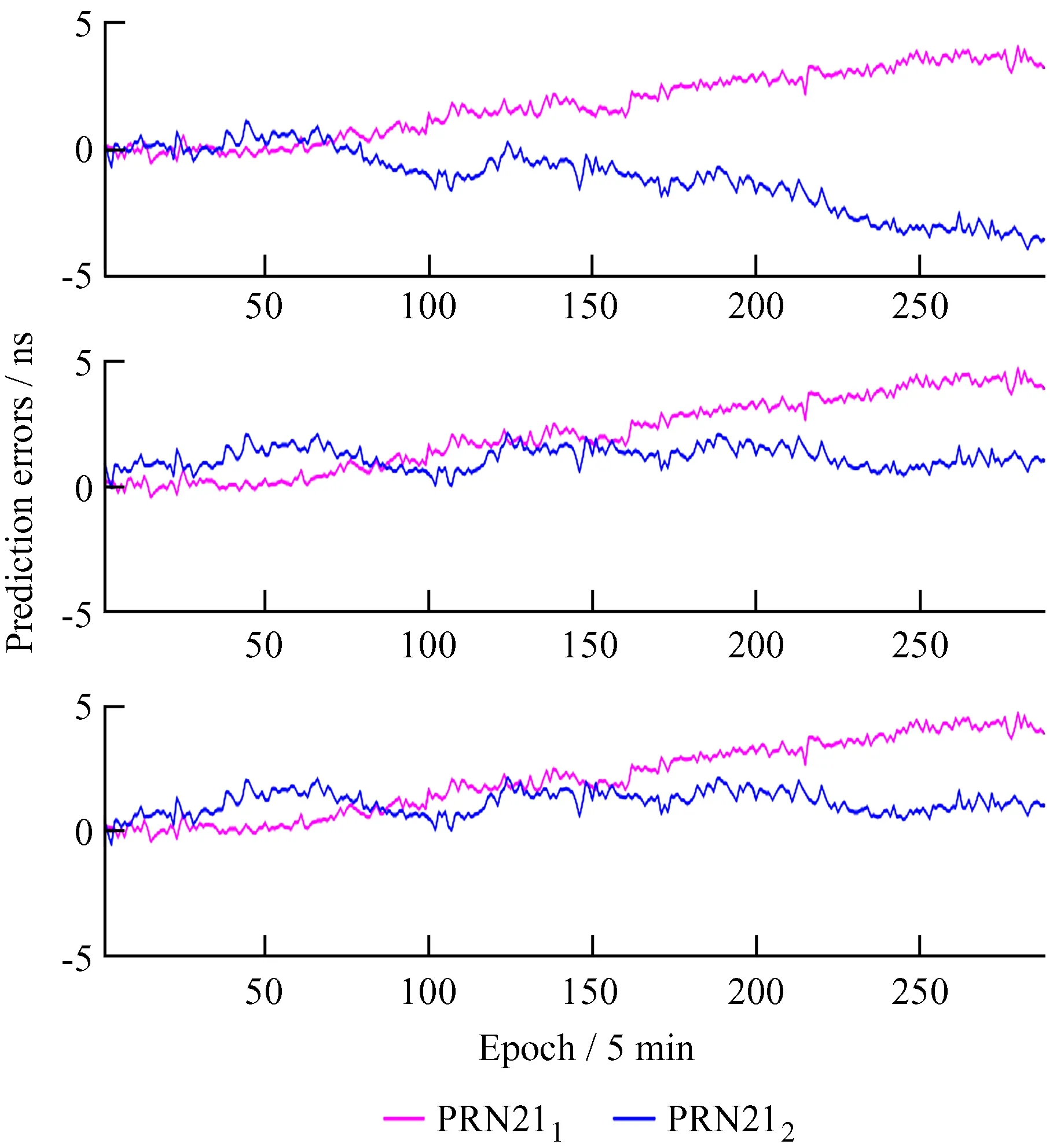
图13 PRN21预报误差对比Fig.13 Prediction errors comparison of PRN21

对图12～图13和表2分析可知：

表2 钟差波动时预报结果统计(单位： ns)Table 2 Statistics of prediction results when clock bias fluctuates (unit: ns)

(1)原始钟差序列波动对预报结果有一定影响，对比不同模型的预报结果可以看出，当钟差序列变化趋势平稳时，预报误差总体上变化较为平缓，且变化幅度小，预报精度高。PRN121和PRN122采用二次多项式模型、灰色模型和灰色 + 自回归模型预报误差的均方根误差PRN121分别提高了18.6%，32.0%和9.6%；PRN211和PRN212采用二次多项式模型、灰色模型和灰色 + 自回归模型预报误差的均方根误差分别为2.191 ns，2.572 ns，2.572 ns和1.675 ns，1.261 ns，1.240 ns，PRN212的预报精度较PRN211分别提高了23.6%，51.0%和51.8%。

(2)不同模型的预报结果与钟差序列的波动幅度大小有关。当钟差序列波动较大时，灰色 + 自回归模型的预报效果较好，PRN121采用灰色 + 自回归模型的预报精度较二次多项式模型和灰色模型分别高了36.2%和34.9%，当钟差序列波动幅度不大时，二次多项式模型的预报效果较好，PRN211采用二次多项式模型的预报精度较灰色模型和灰色 + 自回归模型分别高了14.8%和14.8%。

3 结 论

本文选取3种预报模型从不同角度对全球定位系统星载原子钟的钟差预报进行了研究，结果表明：

(1)从不同类型原子钟的预报结果可知，铷钟短期预报的稳定性总体上优于铯钟，但根据预报模型不同，铯钟的预报精度也可与铷钟相当。灰色模型和灰色 + 自回归模型对于铷钟和铯钟的预报结果均比较稳定，误差变化幅度不大，且预报精度相差不多，但二次多项式模型对铯钟的预报误差波动幅度较大，而铷钟预报误差的波动幅度较小，可与灰色模型和灰色 + 自回归模型相当。总体来说，当建模序列为24 h时，采用灰色 + 自回归模型的预报效果最好。

(2)不同模型、不同长度的钟差序列建模预报效果不同。二次多项式模型受建模序列长度的影响最大，灰色 + 自回归模型受到的影响最小，灰色模型的预报效果随建模序列长度变化的趋势与灰色 + 自回归模型相似；采取不同模型预报时，不同类型原子钟的最佳序列长度也有所区别；另外，在一定程度上，铷钟受建模序列长度的影响小于铯钟，但当建模序列增加时，铷钟和铯钟的预报精度趋于稳定。

(3)当建模序列长度为24 h时，钟差序列变化趋势稳定时的预报结果优于钟差序列波动时的结果，当钟差波动幅度不同时，不同预报模型受到的影响也有所差别。