预应力混凝土框架抗连续倒塌压拱承载力研究

黄远 胡晓芳 易伟建

摘   要：为了研究预应力混凝土框架抗连续倒塌的压拱机制承载力，首先建立了有黏结预应力框架非线性有限元分析模型，并采用试验数据对分析模型进行了验证，在此基础上研究了有黏结预应力框架与普通钢筋混凝土框架在连续倒塌过程中压拱受力机制的区别，并分析了预应力框架压拱机制承载力的影响因素. 研究表明：预应力的施加会增加压拱效应，减弱边柱的破坏，但会加剧中柱的破坏. 非预应力筋配筋率、梁高和跨度对压拱机制承载力Fa.u影响较大，顶部非预应力筋配筋率从0.66%增加到1.32%时，Fa.u增加了19.6%，底部非预应力筋配筋率从0.66%增加到1.32%时，Fa.u增加了31.5%;梁高从700 mm增加到900 mm时，Fa.u增大了220.7%，跨度从9 m增加到15 m时，Fa.u减小了64.0%. 柱截面尺寸较小时，增大柱截面尺寸对Fa.u的影响较大;但柱截面尺寸较大时，增大柱截面尺寸对Fa.u的影响较小. 预应力筋配筋率和初始张拉控制应力对Fa.u的影响较小.

关键词：预应力混凝土框架;有黏结;精细有限元;连续倒塌;压拱机制;承载力

中图分类号：TU378                             文献标志码：A

Abstract：In order to investigate the progressive collapse capacity of prestressed concrete frame structures， we established a nonlinear finite element model of a bonded-prestressed concrete frame. The experimental data were used to verify the model. On this basis， the differences of mechanical mechanism between bonded prestressed frame and reinforced concrete frame in the process of progressive collapse were studied， and the influencing factors of the first peak bearing capacity of prestressed frame were analyzed. The studies show that the application of prestress enhances the arch compression effect and weakens the failure of the side column， but it aggravates the failure of the middle column. The ratio of reinforcement， depth of beam and span have great influence on the bearing capacity of arch compression（Fa.u）. When the top reinforcement ratio increased from 0.66% to 1.32%，Fa.u increased by 19.6%. When the bottom reinforcement ratio increased from 0.66% to 1.32%， Fa.u increased by 31.5%. When the depth of beam increased from 700 mm to 900 mm，Fa.u increaseds by 220.7%. When the span increased from 9 m to 15 m，Fa.u decreaseds by 64.0%. When the size of column section is small，increasing the size of column section has a great influence on Fa.u. However，when the column section size is large，increasing the column section size has little influence on Fa.u. The initial tensile control stress and  tendon area have little effect on Fa.u.

Key words：prestressed concrete;bonded;finite element analysis;collapse analysis;compressive arch mechanism;bearing capacity

连续倒塌是指由于意外事件造成结构初始局部破坏，并引起连锁反应导致破坏向结构其他部分扩散，最终使结构大面积坍塌. 目前国内外许多学者已对结构连续倒塌性能进行了相关研究. Sasani等[1]对10层钢筋混凝土（RC）建筑进行了原位试验，分析了结构内力重分布的影响. 易伟建等[2]对二维RC框架进行了有限元分析，提出了计算RC框架结构体系可靠度的方法. 周云等[3]对RC子结构进行了有限元分析，研究了角柱失效时间和横向水平约束刚度对结构抗连续倒塌性能的影响. Kim等[4]研究表明预应力筋加固能够显著提高结构的抗倒塌能力. Qian等[5]研究了均布荷載、无黏结预应力筋、初始预应力及跨高比对梁柱子构件抗倒塌能力的影响.

已有的混凝土结构抗连续倒塌的研究对象主要针对普通钢筋混凝土框架结构或者采用预应力筋作为加强方式的普通钢筋混凝土框架结构. 而对于实际预应力混凝土框架结构的抗连续倒塌研究相对较少. 与普通钢筋混凝土框架结构相比，预应力混凝土框架结构具有荷载重、跨度大和配筋复杂的特点，其抗连续倒塌性能尚不明确，有必要进行相关的研究. 由于无黏结预应力混凝土对锚具可靠性依赖强，安全性较低. 在工程重要构件中，宜优先采用有黏结预应力混凝土[6]. 因此本文选取有黏结预应力框架进行研究.

框架结构抗连续倒塌受力机制主要包括小变形下的压拱机制和大变形下的悬链线机制. 对于预应力混凝土框架，由于结构的楼层高度相对梁跨度和截面高度较小，结构在发生连续倒塌时难以充分发挥悬链线机制，另外楼面梁的竖向变形须达到一定程度时，悬链线机制承载力才会比压拱机制承载力更高，且悬链线机制承载力与钢筋伸长率等不确定因素相关，难以准确估计，因此通常采用压拱机制承载力作为结构抗连续倒塌承载力[7].

本文采用有限元软件Marc建立有黏结预应力混凝土（BPC）框架非线性有限元分析模型，在试验验证基础上，研究BPC框架在连续倒塌过程中的受力机制，并进行参数分析，研究初始张拉控制应力、非预应力筋配筋率、预应力筋配筋率、预应力筋线型、截面尺寸和跨度等参数对BPC框架压拱承载力的影响.

1   有限元模型的建立及验证

1.1   有限元模型的建立

采用有限元软件MSC.Marc对梁柱子结构进行竖向连续倒塌模拟，有限元模型如图1所示. 本文中混凝土选用Solid7号实体单元，钢筋选用Truss9号桁架单元. 不考虑钢筋和混凝土之间的黏结-滑移，采用“Inserts”命令将钢筋嵌入混凝土中.

混凝土单轴受压应力-应变关系采用Rush模型，如图2（a）所示. 凝土的受拉应力-应变关系（σ-ε）采用双线性模型，如图2（b）所示. 混凝土弹性模量Ec按公式（1）计算，软化模量取0.1Ec，泊松比为0.2. 钢筋σ-ε采用双折线模型，如图2（c）所示，弹性模量Es为2.0 × 105 MPa，泊松比取0.3. 预应力筋σ-ε按公式（2）计算[8]. 式中：E0 = 1.95 × 105;f0.2 = 0.85 fb，fb为预应力筋的极限应力，预应力筋的屈服点取0.75 fb，如图2（d）所示. 为了保证有限元模型计算的收敛性，混凝土、钢筋、预应力筋单元均采用Von Mises屈服准则[9].

采用降温法施加预应力，降温幅ΔT=F/（βEp Ap），F为施加的有效预拉力，β为预应力筋热膨胀系数，Ep和Ap分别为预应力筋的弹性模量和面积. 对于有黏结预应力筋，与普通钢筋一样，采用“Inserts”命令嵌入混凝土中.

DOD规范将0.2L作为连续倒塌的极限位移，L为单跨梁长度[10]. 当跨度大于10 m时，采用预应力结构比较经济[11]. 对于跨度大于10 m的预应力结构，采用0.2L作为连续倒塌的失效准则时，结构净高较小，不满足安全的生存高度. 施炜等[12]直接以倒塌的真实物理定义“结构丧失竖向承载力而不能维持保障人员安全的生存空间”作为倒塌的判据. 因此本文分析中的极限位移取层高的1/3[12].

约束边柱底面所有节点六个方向的自由度来模拟固定端. 对于试验装置无法提供有效的侧向约束时，采用非线性弹簧来模拟侧向约束. 在失效柱上端采用位移加载来模拟梁所受的竖向荷载.

打开Non-Positive Definite和Large Strain选项，采用Newton-Raphson平衡迭代法进行非线性求解.

1.2   有限元模型的验证

选取BPC抗连续倒塌试件bonded strand[4]进行模型验证，该试件采用水平加载，模拟时不考虑自重，模型计算结果和试验结果对比如图3（a）所示，二者吻合良好. 由于已有文献中关于BPC框架抗连续倒塌的试验较少，为了进一步验证模型的正确性，选取有黏结预应力框架YKJ1试件[13]以及普通混凝土抗连续倒塌试件B2、B3[14]和P1[15]进行验证. 有限元计算结果与试验结果对比如图3（b）～（e）所示，有限元模型的计算结果与试验结果均吻合良好，说明有限元模型参数选取合理，计算结果准确，可以用于有黏结预应力框架抗连续倒塌研究.

2   预应力框架受力机理分析

为了研究预应力框架的受力机理，设计了2个梁柱子构件，YKJ-1为有黏结预应力框架，初始张拉控制应力为0.5fptk;YKJ-2的尺寸和配筋与YKJ-1相同，但初始张拉控制应力为0. 预应力筋采用1860级高强钢绞线，预应力筋线型采用工程中常用的曲线形. 试件预应力筋布置和几何尺寸如图4所示.

边柱底端均为固定端[15]，在建模时，约束边柱底面所有节点六个方向的自由度来模拟固定端. 对于基准模型，中柱失效前，预应力和重力荷载作用下的初始预应力状态为：梁端底部受拉，顶部受压，梁跨中顶部受拉，底部受压.

YKJ-1和YKJ-2子结构的荷载位移曲线如图5所示，YKJ-1和YKJ-2压拱承载力Fa.u分别为437 kN和407 kN. 为了量化压拱机制对抗倒塌承载力的影响，定义压拱承载力提高系数η = Fa.u /Fj.u ，式中Fj.u为经典塑性铰理论承载力. YKJ-1和YKJ-2的承载力如表1所示，YKJ-1试件承载力高，η值大，说明预应力的施加会增强压拱效应.

YKJ-1和YKJ-2构件边柱梁端顶部预应力筋和非预应力筋应力如图6所示，图中圆点表示压拱承载力Fa.u对应的应力. 对于YKJ-1试件，预应力的施加使得梁端顶部受压，相对于YKJ-2试件，非预应力筋应力有所延迟. 在达到Fa.u时，两者非预应力筋均已屈服，应力基本相同. 在达到Fa.u时，YKJ-2的預应力筋应力远小于YKJ-1的预应力筋应力，且并未达到屈服应力，预应力筋并未充分发挥其性能，所以 η偏小.

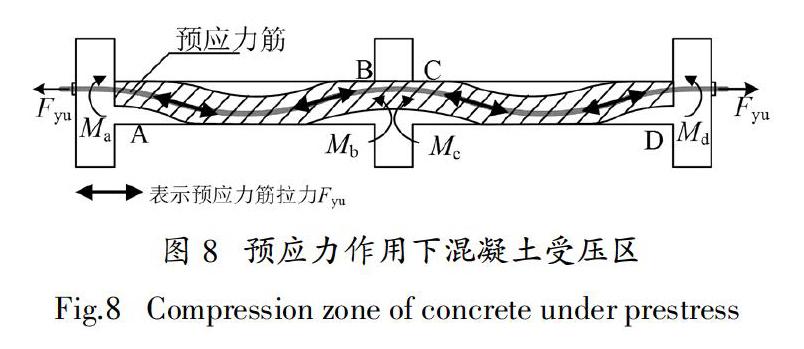
对于未施加预应力结构YKJ-2，梁在压拱机制阶段，其受力情况如图7所示，图中阴影部分为受压区混凝土. 对于施加了预应力的框架子结构YKJ-1，在预应力作用下，其受压区如图8所示，图中阴影部分为受压区混凝土. 预应力使构件中存在反拱，与图7中的受压拱相叠加，使得结构底部受压区的长度增大，但梁顶部受压区长度会减小.

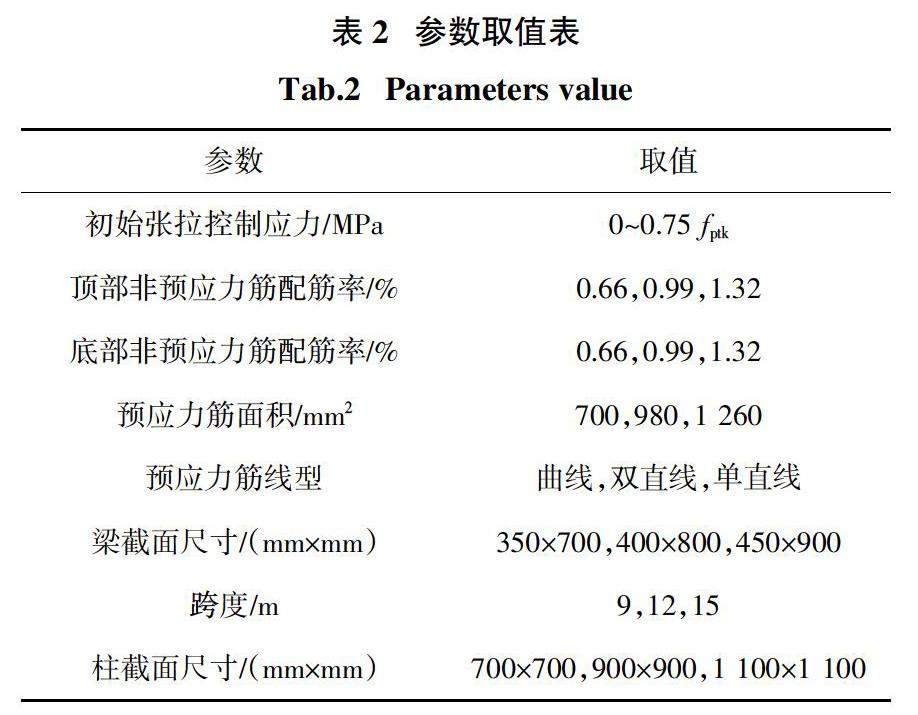
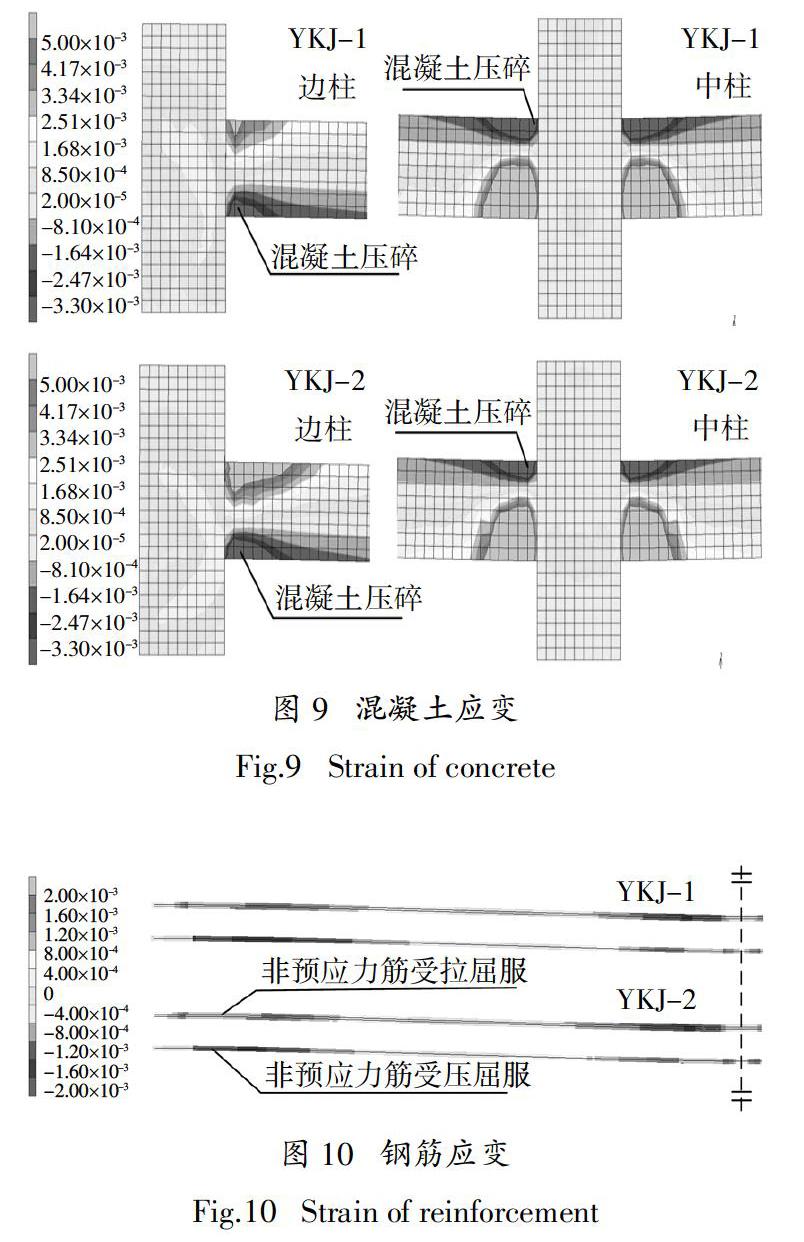
在达到压拱机制承载力Fa.u时，YKJ-1和YKJ-2构件混凝土应变如图9所示，非预应力筋应变如图10所示. 与YKJ-2框架相比，YKJ-1框架中柱梁端混凝土压碎的和钢筋受压屈服区域较大，而边柱梁端混凝土压碎的和钢筋受拉屈服区域较小，对于曲线型预应力筋，预应力的施加可以减小边柱位置梁端的损伤，但会加剧中柱附近梁端损伤.

3   BPC压拱机制承载力影响因素

选取跨度为12 m的框架，对BPC框架的压拱承载力做参数分析. 基准模型为上述的YKJ-1试件，几何尺寸及配筋如图4所示. 参数分析时每次改变一个参数的取值，同时保持基准模型的其他参数不变，各参数取值如表2所示.

3.1   初始张拉控制应力

为了研究初始预应力对压拱承载力的影响，选取初始张拉控制应力σcon分别为0、0.1 fptk、0.2 fptk、0.3 fptk、0.4 fptk、0.5 fptk、0.6 fptk、0.75 fptk的模型进行分析，fptk为预应力筋强度标准值. 各结构的压拱承载力Fa.u和压拱承载力提高系数η如图11（a）所示.

压拱承载力随着初始张拉控制应力的增大而增大，且初始张拉控制应力较大时，压拱承载力增加较慢. 初始张拉控制应力从0增加到0.75 fptk时，Fa.u增加了8.4%，η增大了8.8%.

3.2   顶部非预应力筋配筋率

不同顶部配筋率下，各结构的Fa.u和η值如图11（b）所示. Fa.u随着顶部配筋率的增加而增加，但η随着顶部配筋率的增大而减小. 顶部配筋率增加会使经典塑性铰理论承载力增加，且增加的幅度大于Fa.u，所以η会降低. 顶部配筋率从0.66%增加到1.32%时，Fa.u增加了19.6%，η减小了9.0%.

3.3   底部非预应力筋配筋率

不同底部配筋率下，各结构的Fa.u和η值如图11（c）所示. Fa.u随着底部配筋率的增加而增加，但η随着顶部配筋率的增大而减小. 底部配筋率增加会使经典塑性铰理论承载力增加，且增加的幅度大于Fa.u，所以η会降低. 底部配筋率从0.66%增加到1.32%时，Fa.u增加了31.5%，η减小了2.6%. 相对于顶部配筋率，底部配筋率对承载力的影响更大. 在抗倒塌设计时，宜优先增加底部非预应力筋的面积来提高预应力框架的抗倒塌能力.

3.4   预应力筋面积

预应力筋面积（Ap）对Fa.u和η值影响如图11（d）所示. Fa.u随预应力筋面积的增加而增加，但η随着预应力筋面积的增大而减小. Ap从700 mm2增加到1 260 mm2，Fa.u增加了7.3%，而η降低了42.8%. 随着Ap的增加，Fa.u增加不大，预应力筋面积对Fa.u的影响较小，但会使η显著降低.

3.5   预应力筋布置

保持预应力筋面积不变，改变预应力筋的布置方式，研究预应力筋布置对压拱承载力的影响. 曲线型为基准试件，中间直线和双直线预应力筋布置如图12所示.

不同布置方式计算结果如图11（e）所示. 中间直线与曲线的承载力基本相同，双直线布置的框架承载力最高，比中间直线布置的框架高8.9%. 说明预应力筋的布置方式对结构的承载力有影响，应合理布置预应力筋来提高预应力框架的抗倒塌能力.

3.6   梁截面高度

梁高对预应力框架Fa.u和η值的影响如图11（f）所示. Fa.u随着梁高的增大而增大，η随着梁高的增大而减小. 梁高从700 mm增加到900 mm，Fa.u增加了220.7%，η减小了12.6%.

3.7   跨  度

跨度对预应力框架Fa.u和η值的影响如图11（g）所示. Fa.u和η随着跨度的增大而减小. 跨度从9 m增加到15 m，Fa.u减小了64.0%，η减小了3.8%. 随着跨度的增大，结构承载力急剧下降，相对小跨度的结构，大跨结构在发生初始损伤后更易于造成连续倒塌，抗倒塌设计时应更加重視.

3.8   柱截面尺寸

柱截面尺寸对预应力框架Fa.u和η值的影响如图11（h）所示. 当柱截面尺寸较小时，增大柱截面尺寸，Fa.u会显著增大;当柱截面尺寸较大时，增加柱截面尺寸对Fa.u的影响并不明显.

4   结   论

本文采用有限元软件Marc建立BPC框架，研究BPC框架在连续倒塌过程中的受力机制以及压拱承载力影响因素，得到结论如下：

1）预应力的施加，会增大压拱承载力Fa.u，增强压拱效应，减弱边柱的破坏，但会加剧中柱的破坏.

2）非预应力筋配筋率、梁高和跨度对压拱机制承载力Fa.u影响较大，顶部配筋率从0.66%增加到1.32%时，Fa.u增加了19.6%，底部配筋率从0.66%增加到1.32%时，Fa.u增加了31.5%;梁高从700 mm增加到900 mm时，Fa.u增加了220.7%;跨度9 m增加到15 m时，Fa.u减小了64.0%.

3）柱截面尺寸较小时，增大柱截面尺寸对Fa.u的影响较大;但柱截面尺寸较大时，增大柱截面尺寸对Fa.u的影响较小. 预应力筋配筋率和初始张拉控制应力对Fa.u的影响较小.

参考文献

[1]   SASANI M，BAZAN M，SAGIROGLU S. Experimental and analytical progressive collapse evaluation of actual reinforced concrete structure [J].  ACI Structural Journal，2007，104（6）：731—739.

[2]    易伟建，邓茜. 基于OpenSees的钢筋混凝土平面框架抗连续倒塌能力分析[J]. 湖南大学学报（自然科学版），2019，46（5）：1—10.

YI W J，DENG Q. Analysis of progressive collapse resistance capability of reinforced concrete plane frames based on OpenSees [J]. Journal of Hunan University （Natural Sciences），2019，46（5）：1—10. （In Chinese）

[3]    周云，胡翔，陈太平，等. 混凝土框架子结构角柱快速移除数值分析[J]. 湖南大学学报（自然科学版），2019，46（7）：19—26.

ZHOU Y，HU X，CHEN T P，et al. Numerical analysis on corner column sudden removal of RC frame substructure [J]. Journal of Hunan University （Natural Sciences），2019，46（7）：19—26. （In Chinese）

[4]   KIM J，CHOI H. Monotonic loading tests of RC beam-column subassemblage strengthened to prevent progressive collapse[J]. International Journal of Concrete Structures and Materials，2015，9（4）：401—413.

[5]  QIAN K，LIU Y，LI B. Progressive collapse resistance of posttensioned concrete beam-column subassemblages with unbonded posttensioning strands [J]. Journal of Structural Engineering，2018，144（1）：04017182.

[6]    苏健，孙宗光，易南概，等. 无黏结与有黏结预应力混凝土梁抗震性能的试验对比研究[J]. 工程力学，2013，30（5）：69—74.

SU J，SUN Z G，YI N G，et al. Experimental study on seismic performance of unbonded and bonded prestressed concrete beams[J]. Engineering Mechanics，2013，30（5）：69—74. （In Chinese）

[7]    SU Y P，TIAN Y，SONG X S. Progressive collapse resistance of axially-restrained frame beams [J]. ACI Structural Journal，2009，106：600—607.

[8]    过镇海，时旭东. 钢筋混凝土原理和分析[M]. 北京：清华大学出版社，2003：136—137.

GUO Z H，SHI X D. Reinforced concrete theory and analysis [M]. Beijing：Tsinghua University Press，2003：136—137. （In Chinese）

[9]    陶慕轩，聂建国. 预应力钢-混凝土连续组合梁的非线性有限元分析[J]. 土木工程学报，2011，44（2）：8—20.

TAO M X，NIE J G. Nonlinear finite element analysis of prestressed continuous steel concrete composite beams[J]. China Civil Engineering Journal，2011，44（2）：8—20. （In Chinese）

[10]  DOD 2010 Design of structures to resist progressive collapse [S]. Washington DC：Department of Defense，2010：57—70.

[11]  李晨光，薛伟辰，邓思华. 预应力混凝土结构设计及工程应用[M]. 北京：中国建筑工业出版社，2013：7—8.

LI C G，XUE W C，DENG S H. Design and engineering application of prestressed concrete structure [M]. Beijing：China Architecture & Building Press，2013：7—8. （In Chinese）

[12]  施炜，叶列平，陆新征，等. 不同抗震设防RC框架结构抗倒塌能力的研究[J]. 工程力学，2011，28（3）：41—48.

SHI W，YE L P，LU X Z，et al. Study on the collapse-resistant capacity of RC frames with different seismic fortification levels [J].Engineering Mechanics，2011，28（3）：41—48. （In Chinese）

[13]  李作勤. 預应力混凝土框架抗震性能试验研究及分析[D]. 重庆：重庆大学土木工程学院，2006：17—48.

LI Z Q. Research on the seismic behaviors of prestressed concrete frame [D]. Chongqing：College of Civil Engineering，Chongqing University，2006：17—48. （In Chinese）

[14]  初明进，周育泷，陆新征，等. 钢筋混凝土单向梁板子结构抗连续倒塌试验研究[J]. 土木工程学报，2016，49（2）：31—40.

CHU M J，ZHOU Y L，LU X Z，et al. An experimental study on one-way reinforced concrete beam-slab substructures for resisting progressive collapse [J]. China Civil Engineering Journal，2016，49（2）：31—40. （In Chinese）

[15]  QIAN K，LI B，MA J. Load-carrying mechanism to resist progressive collapse of RC buildings [J]. Journal of Structural Engineering，2015，141（2）：04014107.