基于衰变三分扰动蜻蜓算法的医学图像配准

杜晓昕 张剑飞 王一萍 金梅 梁伟

摘  要： 针对基本蜻蜓算法因进化运动不稳定，从而引发收敛速度减慢等不足，提出衰变扰动方法和三分扰动方法，采用衰变扰动方法提升基本蜻蜓算法的寻优能力，采用三分扰动方法增强蜻蜓群体的富集性，进而提出一种衰变三分扰动蜻蜓算法。针对基本Powell算法依赖于初始点和易陷入局部极值等不足，采用衰变三分扰动蜻蜓算法对Powell进行优化，将其用于医学图像配准优化技术中，采用互信息作为评价标准，提出一种衰变三分扰动蜻蜓算法优化Powell的医学图像配准方法。通过仿真实验表明，该方法提高了医学图像配准的精度和鲁棒性。

关键词： 衰变扰动; 三分扰动; 蜻蜓算法; Powell; 互信息; 医学图像配准

中图分类号： TN911.73?34; TP391.41             文献标识码： A                    文章编号： 1004?373X（2020）04?0149?04

Method of medical image registration based on dragonfly algorithm with decay and tripartite disturbances

DU Xiaoxin， ZHANG Jianfei， WANG Yiping， JIN Mei， LIANG Wei

（College of Computer and Control Engineering， Qiqihar University， Qiqihar 161006， China）

Abstract： The decay disturbance method and the tripartite disturbance method are proposed for the problem that the evolutionary motion of the basic dragonfly algorithm is instable， which leads to the slow convergence speed and other shortcomings. The decay disturbance method is used to improve the optimization ability of the basic dragonfly algorithm， the tripartite disturbance method is used to enhance the enrichment ability of the dragonfly population， and then the dragonfly algorithm with decay tripartite disturbance is proposed. As the basic Powell algorithm depends on the initial point and is easy to fall into the local extremum， the dragonfly algorithm with decay and tripartite disturbances is used to optimize Powell， and applied to the medical image registration optimization technology. A medical image registration method is proposed， which utilizes the dragonfly algorithm with decay and tripartite disturbances to optimize Powell， and for which the mutual information is taken as its evaluation criteria. The simulation experimental results show that this method can improve the accuracy and robustness of medical image registration.

Keywords： decay disturbance; tripartite disturbance; medical dragonfly algorithm; Powell; mutual information;medical image registration

0  引  言

当前医学图像分析技术在临床辅助诊断中发挥着重要的作用，不同医疗设备拍摄的各类医学图像呈现了不同的医学信息，医生为了获得患者更加丰富的辅助诊断信息，必须要对多种医学图像进行融合以实现精准的治疗[1?2]。医学图像融合核心技术之一是医学图像配准，它是计算机技术医学应用领域的研究热点[3]。在医学图像配准中一个重要核心是优化技术，优化技术往往直接影响着配准的精确度[4?5]。目前针对于医学图像配准优化技术涌现出了丰富的研究成果，例如单纯形法[6]、单一Powell法[7]和群智能算法（萤火虫群优化方法[8]和布谷鸟优化方法[9]等）。其中单纯形法存在进化速度过缓的弊端[6]，单一Powell法存在易偏离全局最优陷入局部极值的缺陷[7]，萤火虫和布谷鸟等群智能算法也存在模型过于复杂、优化过程可控性差等问题[8?9]。

Seyedali Mirjalili提出了一种新型群智能算法：蜻蜓算法[10]（Dragonfly Algorithm，DA）。蜻蜓算法模拟了生物界蜻蜓的群体行为，较其他群智能算法具有建模速度快和人工干扰参数少等特点。目前DA已经较好地应用在信号检测与识别、优化预测模型和故障诊断等，已经成为群智能算法领域一个研究新亮点。随着对DA不断深入地研究，发现DA进化过程中个体之间信息交换不足，种群的多样性不断减弱，收敛速度减慢，不能保证全局搜索能力趋于稳定，易陷入局部极值，从而导致进化运动不稳定。本文在面向医学图像配准应用的基础上改进提升DA的优化计算能力，提出一种衰变三分扰动蜻蜓算法（Dragonfly Algorithm of Decay Tripartite Disturbance，DA?DTD），选用DA?DTD和Powell结合方法作为医学图像配准的优化技术，选用互信息作为医学图像配准的测度技术，进而提出了一种衰变三分扰动蜻蜓算法优化Powell的医学图像配准方法（MIR?DA?DTD?P）。

1  衰变三分扰动蜻蜓算法

1.1  衰变扰动

定义1（衰变扰动因子[Γ]）  [Γ]表达了迭代进化过程中扰动的衰变趋势，式（1）给出[Γ]的量化定义：

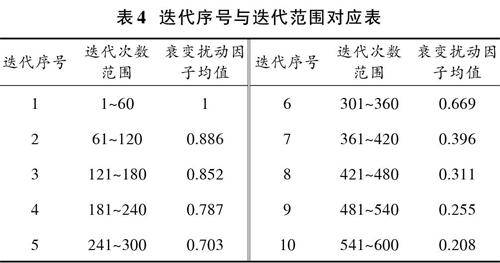
[Γ（I）=1，1≤I≤αeβ-β·IImax-1eβ-β·IImax+1×eβ·IImax-β-11+eβ·IImax-β，α

式中：I为进化当前迭代数;[Imax]为进化最大迭代数;[α]为断点参数;β为归一化倍数。

由式（1）可知，衰变扰动因子[Γ]是以[I]为自变量的函数。当[I∈[1，α]]时，[Γ=1];当[I∈（α，Imax]]时，[Γ]为1～0之间的递减值，该递减值前期为缓慢递减，后期为加速递减。其中，[e]的指数变换形式为将进化迭代数[I]向区间[[0，β]]做归一化处理。衰变扰动因子[Γ]的实际意义为，在进化初期（在[α]代之前）衰变扰动因子值为1，表示衰变扰动未启动;在进化中后期（在[α]代之后）衰变扰动因子为1～0之间的递减值，表示衰变扰动启动，并由1衰减至接近0，在此过程扰动为由强到弱。

定义2（三分扰动因子[ξ]）   [ξ]将进化过程根据[α]一分为三，形成三个不同的阶段，不同阶段执行不同的扰动操作，式（2）给出[ξ]的量化定义，三分扰动具体操作如表1所示。

[ξ=Cauchy（0，1），1≤I≤αT（I），               α

三分扰动因子[ξ]的实际意义为，扰动整体增强了群体的富集性，满足如下3个准则：

准则1 在进化初期（在[α]代之前）使用扰动能力最强的[Cauchy（0，1）]操作，强烈的扰动振荡可以避免迂回于局部极值。

[ [Cauchy（0，1）] [N（0，1）] [T（I）] 具体操作 标准柯西分布 均值为0，均方差

为1的高斯分布 以I为自由度参

数的T分布 扰动能力 最强 最弱 介于前面二者之间 ]

准则2 在进化中期（在[α]代之后，[5-12·Imax]之前）使用扰动能力居中的[T（I）]操作，这样可以保证最优运动的惯性。

准则3 在进化后期[5-12·Imax之后]使用扰动能力最弱的[N（0，1）]操作，此时进化趋近结束，如果强烈的扰动振荡可能会导致失去本次最优值，从而降低计算准确度。

定义3 （衰变三分扰动富集）  蜻蜓个体位置向量为[XMi=x1i，x2i，…，xMiT]（M为向量空间的维数）。对[XMi]进行衰变三分扰动富集操作如下：

[XFMi=XMi+XMi×Γ×ξ        =x1ix2ix3i?xMi+x1ix2ix3i?xMi×Γ×ξ=x1i+x1i×Γ×ξx2i+x2i×Γ×ξx3i+x3i×Γ×ξ        ?xMi+xMi×Γ×ξ]  （3）

式中，[XMi]进行衰变三分扰动富集操作后为[XFMi]。

衰变三分扰动富集操作在蜻蜓个体流逝位置的基础上增添了三分扰动，这样提升了蜻蜓群体的富集性，同时扰动操作受衰变因子的动态调节，衰变因子使扰动随着进化代数动态减小，这样可使计算快速收敛，提高了求解精度。

1.2  衰变三分扰动蜻蜓算法（DA?DTD）

本文在基本DA的基础上加入了衰变三分扰动富集操作，进而提出了衰变三分扰动蜻蜓算法（DA?DTD）。DA?DTD核心环节为衰变三分扰动富集操作的启动规则（见规则1），此外DA?DTD在静态场与动态场中分别执行不同的群活动，DA?DTD执行规则如下：

规则1（衰变三分扰动富集启动）：设群体进化过程中相邻三代分别为[IMi-2，IMi-1，IMi]，启动控制阈为[ω]，当[IMi-2-IMi-1≤ω]和[IMi-IMi-1≤ω]同时满足时衰变三分扰动富集启动。

规则2（静态场中群活动）：执行聚合活动、引食活动和敌斥活动，静态场中群活动具有局部性和随机性。

规则3（动态场中群活动）：执行离散活动、同一活动和聚合活動，动态场中群活动具有方向同一性。

DA?DTD具体流程如下：

1） 给定群体规模，设定最大迭代次数，随机初始化蜻蜓群体位置，初始化最优位置。

2） 启动规则2完成全局位置更新。

3） 启动规则3完成局部位置更新。

4） 计算个体适应度值，在蜻蜓群体中找出适应度值最优的蜻蜓个体位置，判断是否优于上一代，若是执行步骤5），否则执行步骤6）。

5） 保留当前最优位置，使蜻蜓群体向当前最优位置飞行，转向步骤8）。

6） 启动规则1判断最优蜻蜓位置是否满足衰变三分扰动富集启动条件，若是执行步骤7），否则执行步骤8）。

7） 根据式（3）执行衰变三分扰动，转向步骤8）。

8） 是否达到最大迭代次数，若是算法结束，否则转向步骤2）。

2  DA?DTD优化Powell的医学图像配准方法

本文提出一种基于DA?DTD优化Powell的医学图像配准方法（MIR?DA?DTD?P）。MIR?DA?DTD?P采用DA?DTD优化Powell的方法来获得最优配准变换参数，具体步骤如下：

1） 将待配准图像通过金字塔图像分解生成多分辨率图像组。

2） 将分解后的图像组中低分辨率图像采用DA?DTD获得次优变换参数。

3） 将步骤2）获得次优变换参数作为Powell的初始参数。

4） 对分解后图像组中除步骤2）之外的其他分辨率逐层采用步骤3）的Powell获得次优变换参数。

5） 对分解后图像组中除步骤2）之外的其他分辨率逐层采用DA?DTD获得次优变换参数。

6） 判断分解后图像组中所有分辨率层图像是否都求解完次优变换参数，如果不是转到步骤4），否则转到步骤7）。

7） 采用互信息作为评价标准，在步骤4）至步骤6）所有次优变换参数中选择最优变换参数。

8） 根据获得的最优变换参数进行配准变换，获得配准后图像。

3  仿真实验与结果分析

3.1  医学配准图像数据与算法参数设置

本文医学配准图像数据采用的是[McConnell]数据库中的脑[MRI]医学图像，共采用三组数据。三组数据的参数设置如表2所示，实验数据如图1所示。图1a）为原始图像，图1b）为浮动图像，图1c）为应用MIR?DA?DTD?P后的配准图像。DA?DTD比DA增加的额外参数设置见表3，其中[α]选取为通过多次实验设定的经验值。

3.2  DA?DTD衰变三分扰动性能分析

对DA?DTD的前600次迭代平均分成10份，共有10个迭代序号，计算每个迭代序号对应迭代范围内60次迭代的衰减扰动因子均值，结果如表4所示。由表4可知，迭代序号1的衰减扰动因子均值为最大值1，迭代序号10为最小值0.208，其余迭代序号随着迭代次数的不断增加，衰变扰动因子值在1～0.208之间逐渐递减。这说明在DA?DTD进化初期为了获得全局最优解，其扰动能力较强，而在进化后期为了保证其局部开发能力，其扰动能力较弱，如果在后期施加较强的扰动能力，可能导致刚刚获得的全局最优解丢失，而再次陷入局部极值。因此本文提出的DA?DTD既保证了全局寻优能力又保证了局部开发能力。

3.3  结果讨论与分析

本文提出配准方法MIR?DA?DTD?P的配准误差如图2所示。由图2可知，不同的分量均在600代之前均达到了较低的误差，这说明本文方法达到了较好的配准精度;此外图2不同分量配准的收敛速度均在总迭代数的60%处就得到了最优值，这说明本文方法具有较快的求解速度。

此外本文对如下4个方法做了对比分析，它们分别是仅使用Powell的配准方法;基本DA优化Powell的配准方法;文献[11]方法（基于群智能的图像配准方法）;DA?DTD优化Powell的配准方法（MIR?DA?DTD?P）。对比结果见表5所示，由表5可知：MIR?DA?DTD?P的互信息要优于其他三种方法，其中MIR?DA?DTD?P比文献[11]提高了7.22%，比方法2提高了11.17%，比方法1提高了22.97%。在60次配准实验中MIR?DA?DTD?P和文献[11]都达到了100%的成功比率，比方法1提高了12%，比方法2提高了9%，方法1和方法2存在部分失败比率。在平均RMSE中MIR?DA?DTD?P的值最小为0.703 5，方法1的值最大为1.386 1，说明不对Powell进行优化，配准的精度较低，MIR?DA?DTD?P比方法1降低了68.26%，比方法2降低了51.32%，比文献[11]降低了39.67%。上述三个方法综合实验结果说明本文提出的方法获得了较好的配准性能。

4  结  语

本文对基本蜻蜓算法进行改进，提出一种衰变三分扰动蜻蜓算法DA?DTD。DA?DTD既具有全局寻优能力又具有局部开发能力，可快速精确完成参数优化。针对医学图像配准技术，本文对待配准的医学图像进行金字塔图像分解生成多分辨率图像组，采用互信息作为评价准则，采用DA?DTD对Powell进行优化，从而获得配准最优变换参数，进而提出了一种新的医学图像配准方法MIR?DA?DTD?P。最后，采用[McConnell]数据库中的脑[MRI]医学图像进行了仿真实验，结果表明本文提出的方法MIR?DA?DTD?P获得了较好的配准精度，并提高了配准的鲁棒性，具有一定的推广价值。

参考文献

[1] SHAH S K. Regularized surface and point landmarks based efficient non?rigid medical image registration [J]. Computing and informatics， 2018， 37（1）： 244?268.

[2] DONG J Y， LU K， XUE J， et al. Accelerated nonrigid image registration using improved Levenberg?Marquardt method [J]. Information sciences， 2018， 423（1）： 66?79.

[3] PAN M S， JIANG J J， ZHANG F， et al. Medical image registration and fusion using principal component analysis [J]. International Arab journal of information technology， 2017， 14（4）： 512?520.

[4] WAN Yanli， HU Hongpu， XU Yanli. A robust and accurate non?rigid medical image registration algorithm based on multi?level deformable model [J]. Iranian journal of public health， 2017， 46（12）： 1679?1689.

[5] ABDEL?BASSET M， FAKHRY A E， EL?HENAWY I， et al. Feature and intensity based medical image registration using particle swarm optimization [J]. Journal of medical systems， 2017， 41（12）： 197.

[6] PANDA R， AGRAWAL S， SAHOO M， et al. A novel evolutionary rigid body docking algorithm for medical image registration [J]. Swarm and evolutionary computation， 2016， 33： 108?118.

[7] WANG B L， YING C. Liver medical image registration based on biomechanical model [J]. Multimedia tools and applications， 2017， 76（19）： 19927?19944.

[8] 杜晓昕，张剑飞，孙明.基于自适应t分布混合变异的人工萤火虫算法[J].计算机应用，2013，33（7）：1922?1925.

[9] 李荣雨，戴睿闻.自适应步长布谷鸟搜索算法[J].计算机科学，2017，44（5）：235?240.

[10] MIRJALILI S. Dragonfly algorithm： a new meta?heuristic optimization technique for solving single?objective， discrete， and multi?objective problem [J]. Neural computing & applications， 2016， 27（4）： 1053?1073.

[11] WANG Bo， ZHANG Jing， DU Xiaoxin. Biomedical image registration based on fruit fly optimization algorithm with segmented mutation and Powell [J]. ICIC express letters， part B： applications， 2016， 7（1）： 215?221.