一类四阶非线性抛物方程的紧致差分格式
2020-07-23张迪杨青
张 迪 杨 青
( 山东师范大学数学与统计学院, 250358, 济南 )
1 引 言
考虑以下四阶非线性抛物方程的初边值问题:
(1)
其中p为整数且p>1,K1(t),K2(t),K3(t),u0(x)为已知函数且满足一定的光滑性,K2(t)有正的下界.
四阶非线性抛物方程在薄膜理论和润滑理论等方面应用广泛[1-3],文献[4,5]对四阶非线性抛物方程经典解的适定性进行了研究. 特别地, 在文献[4]中主要研究了问题(1)解的爆破现象, 文献[5]中证明了四阶非线性抛物方程精确解的存在性和渐近性, 但此类方程的精确解一般难以求出, 因此对此类方程的数值解的研究具有重要意义. 紧致差分方法可以利用较少节点, 达到较高精度且容易计算, 已被应用于多种微分方程. 文献[6-8]分别对抛物方程、双曲方程以及椭圆方程建立了紧致差分格式. 对于非线性方程, 可以对非线性项线性化处理, 建立方程的线性差分格式, 如文献[9]对几类非线性发展方程建立了线性化差分格式. 文献[10,11]对二阶非线性延迟抛物方程建立了Crank-Nicolson型线性化格式. 相对于二阶抛物方程而言, 求解高阶抛物方程时通常进行降阶处理, 文献[12-14]中均对四阶方程进行了降阶处理.
本文通过引入中间变量将四阶非线性抛物问题(1)转化为二阶非线性方程组, 对方程中的时间导数项采用Crank-Nicolson格式离散, 空间导数项采用四阶紧致差分格式离散, 非线性项则采用外插方法处理, 用前两层的线性组合来逼近未知时间层, 最终得到原问题的三层线性紧致差分格式, 并通过数值算例验证该格式的有效性.
2 紧致差分格式
(2)
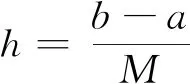

定义紧致差分算子
(3)
引理1[15]如果g(x)∈C6[c-h,c+h], 则有

其中ξ∈(c-h,c+h).
结合紧致差分算子的定义(3)和引理1, 有
(4)
其中ξik∈(xi-1,xi+1).
(5)
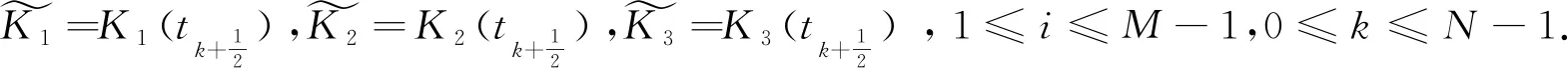
由Taylor展式, 得
(6)
(7)
(8)
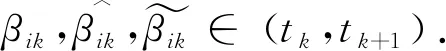
对(5)式中的非线性项, 由(7)式得
(9)
(10)
将(6)~(10)式代入(5)式, 得
(11)
(12)
其中
1≤i≤M-1,1≤k≤N-1,

(13)
其中1≤i≤M-1,1≤k≤N-1.
其次, 在点(xi,tk)处考虑方程(2b), 有
(14)
(15)
将(4)式代入(15)式, 得
(16)


(17)
对初值条件(2c)和边值条件(2d),(2e)进行直接离散得
(18)
(19)
(20)

(21)
(22)
(23)
其中1≤i≤M-1.
(24)
联立(13)式、(17)式以及初边值条件(18)式、(19)式、(20)式, 可得原问题(1)的紧致差分格式为
(25)
由上述推导过程可知, 该紧致差分格式的局部截断误差为O(τ2+h4).
3 数值算例
算例1考虑以下四阶非线性抛物方程的初边值问题:
(26)
其中F(x,t)=(1+π2+π4)etsinπx-etsinπx|etsinπx|.
取问题的精确解为u(x,t)=etsinπx,下面用紧致差分格式(25)来求解问题(26).


表1 N=M2时紧致差分格式解U的误差和空间收敛阶

表2 N=M2时紧致差分格式解V的误差和空间收敛阶
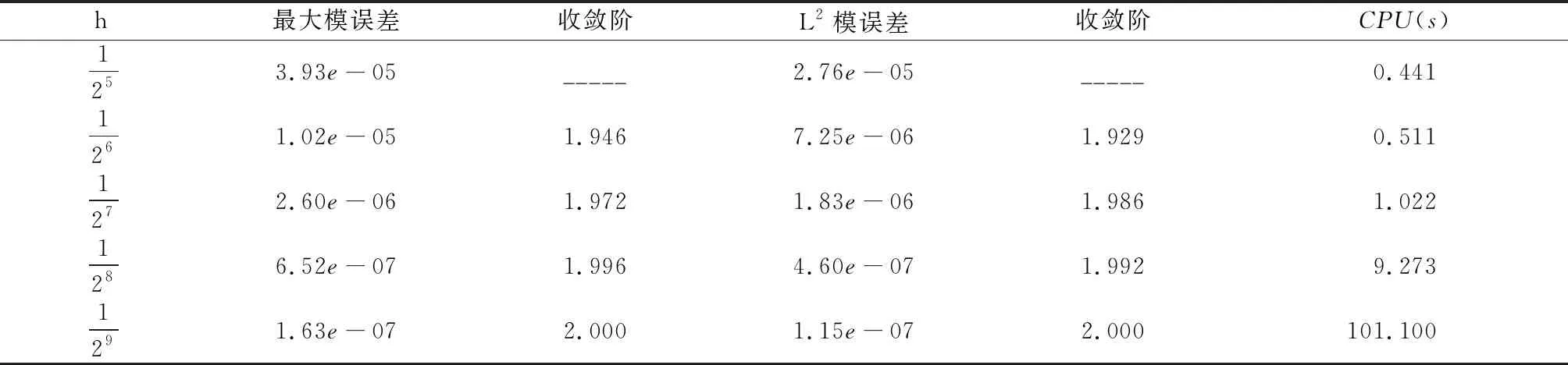
表3 N=M时紧致差分格式解U的误差和时间收敛阶
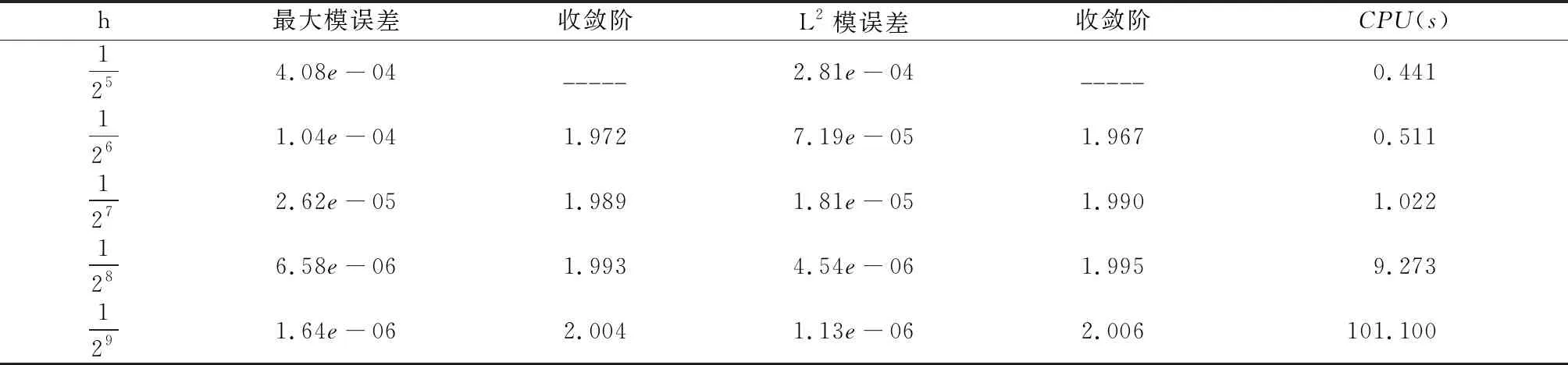
表4 N=M时紧致差分格式解V的误差和时间收敛阶
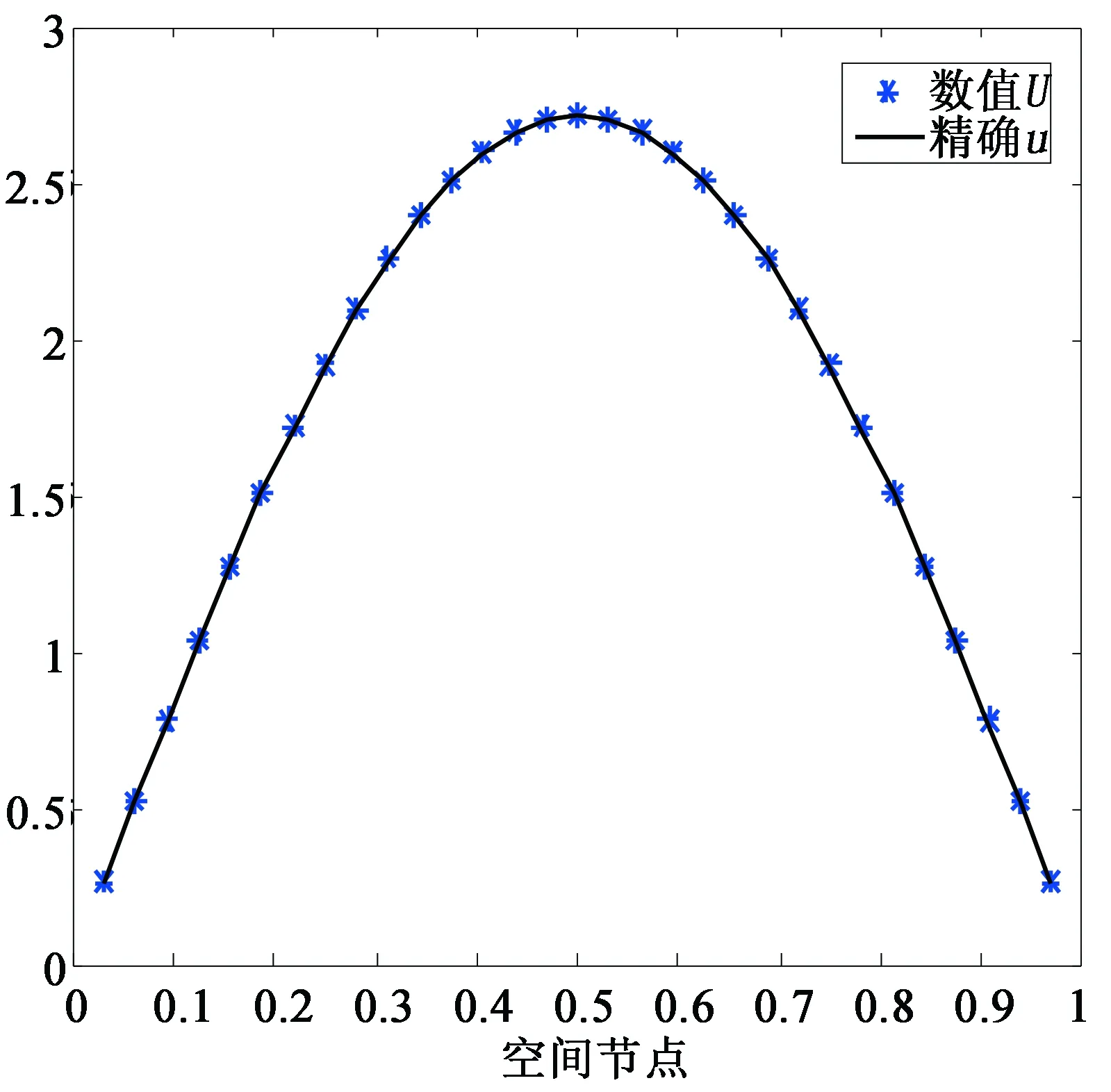
图1 当M=25时, 数值解U与精确解u的拟合图像

图2 当M=25时, 数值解V与精确解v的拟合图像
