基于matlab的柔性直流输电系统建模与仿真

2020-07-23闫伟杨家凯王荣富韩广宇卯明旺

云南电力技术 2020年3期

闫伟，杨家凯，王荣富，韩广宇，卯明旺

（云南电网有限责任公司楚雄供电局，云南楚雄 675000）

0 前言

目前，能源危机日益加剧，环境污染问题日益严重，为了解决这些问题国家将大力发展可再生能源以优化能源结构。然而，由于太阳能和风能等可再生清洁能源具有分散化、小型化、远离负荷中心的特点，势必要求通过远距离、大容量的输电方式将这些清洁能源发出的电能传输，直流输电技术显然是一个好的选择。

多年以来，在传统的高压直流输电系统中采用的是晶闸管作为换流站的开关器件。但由于晶闸管是一种半控型电力电子器件，只具有控制导通能力，而没有自关断能力，且开关频率较低，运行时产生的低次谐波较多，这也就导致了传统的直流输电技术存在一些缺点。

基于以上原因，研究和发展基于VSC和PWM脉宽调制技术的新型输电方式——柔性直流输电，是中国电力工业发展的必然选择。换句话说，发展VSC-HVDC技术将解决城市供电和孤岛供电中存在的问题，促进大规模的以风能、太阳能为代表的清洁能源的并网，满足持续快速增长的能源需求，有利于智能大电网的构建。

所以研究基于VSC的柔性直流输电技术，建立其数学模型，并以此建立可靠的仿真模型，对研究柔性直流输电的控制和保护具有理论和实际的现实意义。

1 柔性直流输电系统原理

典型的双端柔性直流输电（VSC-HVDC）系统基本结构如图1所示。系统两端分别为整流站和逆变站。与常规换流站类似，柔性直流换流站主要由电压源换流器、换流电抗器、换流变压器、直流电容器和交流滤波器组成。整流站与逆变站中间通过直流输电线路连接。

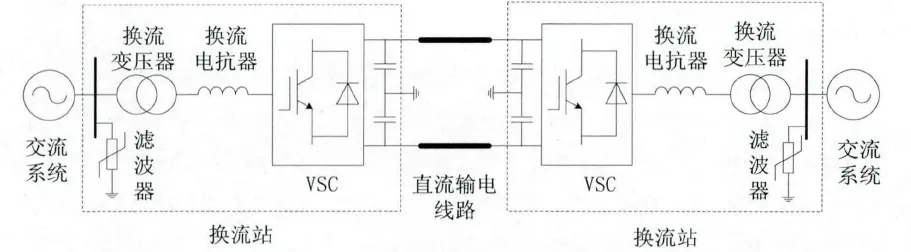
图1 柔性直流输电系统结构图

随着换流器工作状态的调整，系统的功率可以双向流动，即换流器既可以工作在整流状态将从交流系统接收的交流电转化成直流送出，也可以工作在逆变状态将直流系统输送过来的直流电通过转化输送至交流系统中。图2所示为单端电压源型换流器的原理图。

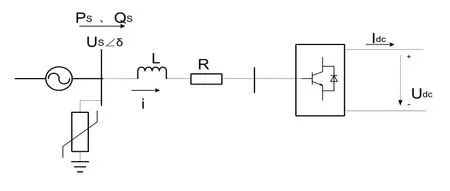
图2 单端电压源换流器原理图

图2中，L为换流器的等效电感，R为换流器的等效电阻，US为交流母线基波电压向量，UC为换流器输出基波电压向量，δ为UC滞后US的角度，PS、QS为交流系统向公共连接点处注入的有功功率和无功功率，PC、QC为换流器输出的有功功率和无功功率。

忽略换流器与变压器损耗及谐波分量时，交流系统向换流器发出的有功功率和无功功率分别为：

式中；

μ——直流电压利用率；

X——换流器电抗；

Udc——直流电压额定值；

M——调制比；

δ——交流系统电压US与换流器输出电压UC的相位差；

从以上公式可以看出：对电压源换流器进行调制时，只要调节相角δ和调制比M即可实现对有功功率PS和无功功率QS的控制。

2 MATLAB/SIMULINK建模

基于上述的理论分析通过MATLAB/SIMULINK软件对系统进行建模。柔性直流输电系统的结构如图3所示，系统两端换流站基于电压源（VSC）构建，换流站主要由电压源换流器、换流电抗器、换流变压器、直流电容器和交流滤波器组成。（注：为方便后续实验，特添加了三相故障模块）系统两端换流站通过直流输电线路连接，一端工作于整流（交流）状态，另一端工作于逆变状态，共同实现两端交流系统间功率传输。

系统主要参数如下：两端交流系统的电压为220 kV，容量为200 MW,频率为50 Hz,直流输电线路的电压为±100 kV，两者之间通过120 km长的线路互联。

图3 基于SIMLINK的VSC-HVDC系统结构图

在本模型中交流系统的结构较为简单，如图4所示模型两端交流系统是完全对称的。主要由一个容量200 MW,电压220 kV的三相电压源、一个电感元件和一个R-L并联电路组成，其中后两者用来模拟实际运行过程中交流系统的电感和阻抗。两端交流系统的电压均为220 kV,频率均为50 Hz,容量均为200 MW。

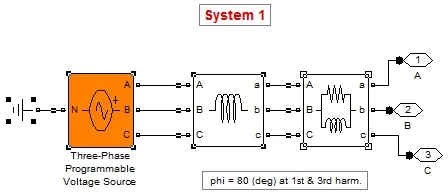
图4 交流系统结构图

由于整流站与逆变站为左右对称系统，以一侧为例，电压源换流站的模型结构如图5所示。换流站主要由换流变压器、换流电抗器、VSC换流电路和滤波器组成。

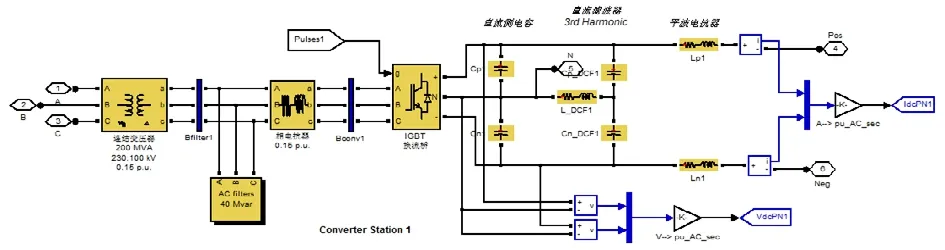
图5 VSC-HVDC换流站系统结构图

其工作原理是：电能由交流系统1传输到换流站，在换流站内先由换流变压器将等级从220 kV降至100 kV；经测量元件B1测量电压、电流相关参数后，又经过交流滤波器和换流电抗器进行滤波；滤波完成后电能传至整流电路（由IGBT组成），整流阀内开关器件的开断由控制系统发出的信号Pluses1进行控制，经整流阀整流后，100 kV的三相交流电被初步转换成±100 kV的直流电；换流阀输出的直流电经直流滤波器、平波电抗器的滤波后变为平滑的直流电输出至直流输电线路；电能经直流电路传到逆变站，在逆变换流站内经过与整流站完全相反的程序，±100 kV直流电被转换成220 kV三相交流电输出至交流系统2。在这个过程中测量与控制系统全面参与，进行了数据的采集和有功无功的控制。

3 仿真实验

3.1 稳态运行实验

系统在大部分情况下均处于稳定运行状态，因此弄清楚VSC-HVDC系统在稳态时的运行方式，控制方式，各个变量的参数变化等情况对于研究VSC-HVDC系统尤为重要。基于上述原因，在MATLAB/SIMULINK仿真平台下搭建双端有源型柔性直流输电系统，并进行稳定运行状态下的实验。VSC-HVDC仿真系统结构图如图3所示，真实模拟系统运行时可能遇到的各种状况在仿真系统处稳态运行时，整流换流器及逆变换流器的各个物理量波形如图6～15所示，以下将对各个波形进行分析：

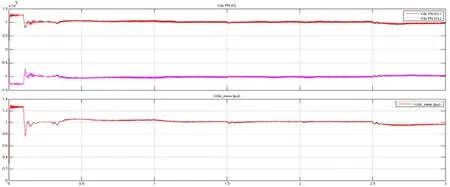
图6（a）整流换流器直流侧直流电压波形

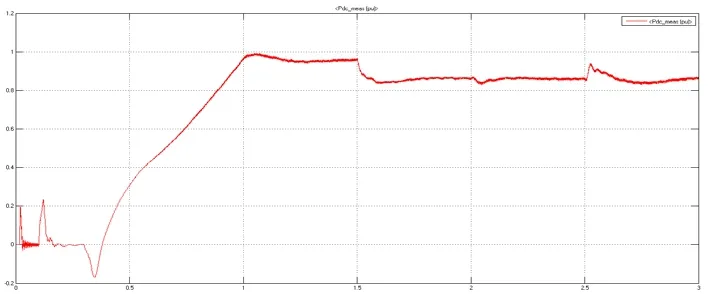
图（b） 6整流换流器直流侧有功功率波形

图6（a）、（b）波形分析：在系统运行开始后，整流换流器直流侧的电压Udc迅速升高至1.25（标幺值）附近；在0.1 s逆变控制系统投入使用后，直流侧电压有一个短暂的降低然后电压维持在1（标幺值）附近波动；在0.3 s整流控制系统投入使用后，直流侧电压逐渐趋于稳定，保持在1×105V附近，此时整流换流器的有功功率Pdc也逐渐提高，最终在1.1 s后稳定于0.95（标幺值），这表明整流换流站正在从交流系统1吸收有功功率，整个系统也在1.1 s后进入稳态；在1.5 s时由于有功功率参考值减小0.1 p.u.，持续时间为0.14 s，直流侧电压、功率均发生一定程度的波动，经过大约0.3 s后重新进入稳态，此时整流器直流侧输出的有功功率降为0.85左右；在2.0 s时由于无功参考功率减小0.1 p.u，直流电压Udc略微降低但有功功率Pdc经过短暂的波动后几乎没有变化，由此验证了VSC-HVDC系统可以独立地控制有功和无功功率。在2.5 s直流电压的参考值下降后直流电压的实际值也下降，说明换流器电压控制部分效果较好。

图7（a）、图7（b）波形分析：在系统运行开始后，逆变换流器直流侧的电压Udc迅速升高至1.25（标幺值）附近；在0.1 s逆变控制系统投入使用后，直流侧电压有一个短暂的降低然后电压维持在1（标幺值）附近波动；在0.3 s整流控制系统投入使用后，直流侧电压逐渐趋于稳定，保持在1×105V附近，此时逆变换流器的有功功率Pdc也逐渐下降，最终在1.1 s后稳定于-0.95（标幺值），这表明逆变换流站在向交流系统2发出有功功率，整个系统也在1.1 s后进入稳态；在1.5 s时由于有功功率参考值减小0.1 p.u.，持续时间为0.14 s，逆变器直流侧电压、功率均发生一定程度的波动，经过大约0.3 s后重新进入稳态，此时逆变器直流侧输出的有功功率降为-0.85左右；在2.0 s时由于无功参考功率减小0.1 p.u，直流电压Udc略微降低但有功功率Pdc经过短暂的波动后几乎没有变化，由此验证了VSC-HVDC系统可以独立地控制有功和无功功率。

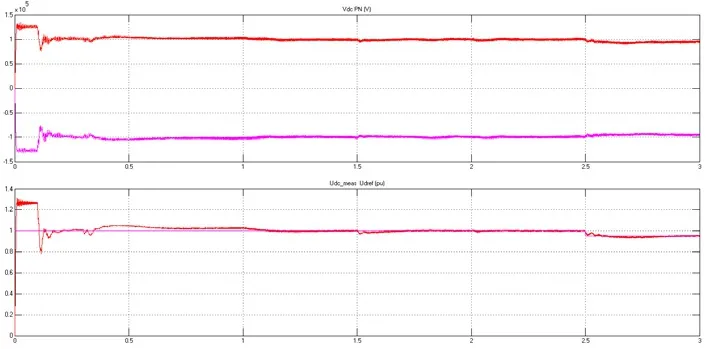
图7（a）逆变换流器直流侧直流电压波形

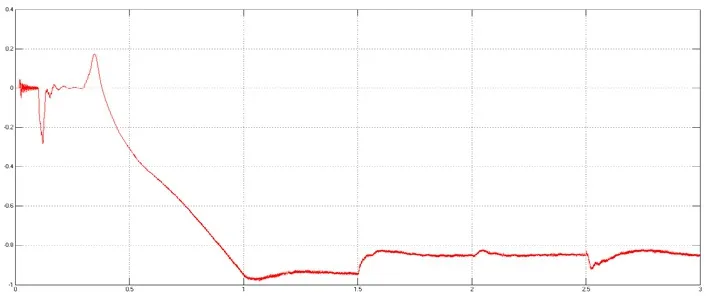
图7（b）逆变换流器直流侧有功功率波形

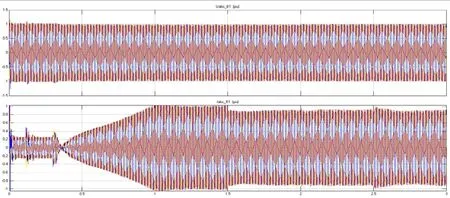
图8 整流换流器交流三相电压和电流波形（标幺值）

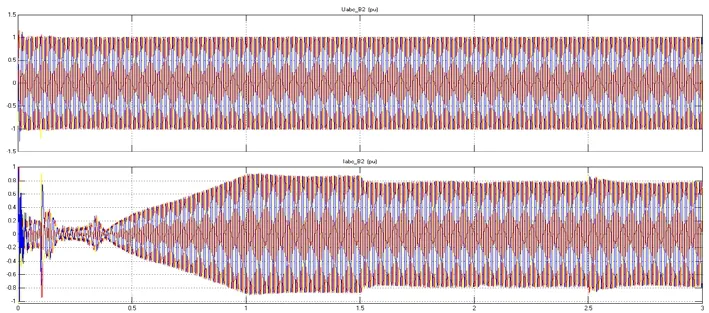
图9 逆变换流器交流三相电压和电流波形（标幺值）

图8波形分析：该图是整流换流器交流三相电压和电流波形图，一开始由交流系统1提供的交流电压很快进入稳定运行状态，而交流电流经过1.1 s左右才进入稳态。这是因为电能从交流系统1经过两个变压站、换流站到交流系统2，建立稳定的功率传输需要一定的时间，这一点在图7的有功功率波形图中也得到体现。在1.5 s时由于有功功率参考值减小0.1 p.u.，持续0.14 s，交流电压、功率均发生一定程度的波动，在波动结束后重新进入稳态，此时交流电流的大小较原来有一定程度的降低，在2.5 s时直流参考电压减小0.05 p.u，但交流电压、电流的大小几乎没有变化，这是因为在本论文的VSC-HVDC系统中送电端系统采用定直流电压控制，受电端系统采用定无功功率控制。

图9波形分析：该图是逆变换流器交流三相电压和电流波形图，与图8对比可发现，整流侧和逆变侧的交流电压、电流均比较平稳，但逆变侧的交流电流大小略小于整流侧，这是因为电能在传输过程中存在能量损耗，由于电压相对固定那么功率的损耗就体现在了电流的减小上。

图10（a）整流换流器交流侧电压测量值波形

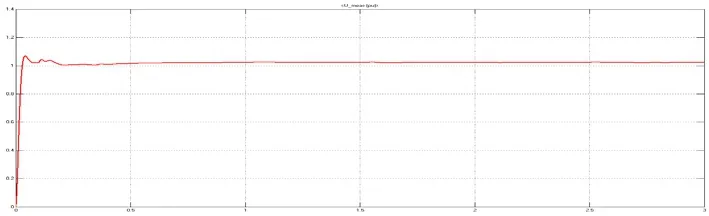
图10(b) 逆变换流器交流侧电压测量值波形

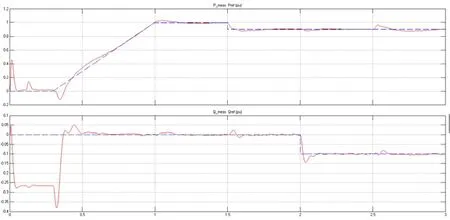
图11（a）整流换流器有功测量值参考值、无功测量值参考值波形

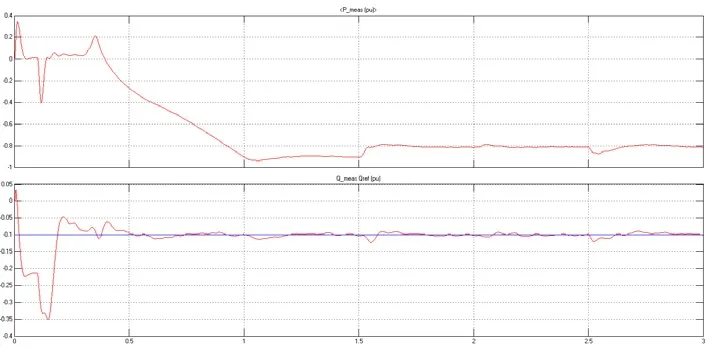
图11(b) 逆变换流器有功测量值参考值、无功测量值参考值波形

图10（a）、10(b)波形分析：图10（a）、10(b)分别是整流换流器交流电压和逆变换流器交流电压测量值（标幺）与时间的关系图像。对比两个图像不难发现逆变换流器的交流电压要比整流换流器平稳得多，这是因为有功功率和无功功率参考值的改变都直接从整流侧的交流系统发起，由于电压控制系统的调控，对逆变侧输出的交流电压并没有产生大的干扰。换句话来说VSC-HVDC系统在某种程度上可以起到故障隔离的作用，当一端交流系统发生小的扰动（在调节范围内的扰动）并不会影响另一端交流系统的正常运行，供电质量也不会受到影响。

图11（a）、11(b)波形分析：图11（a）、图11(b)分别是整流器和逆变器的有功测量值参考值、无功测量值参考值波形。从图中可看出，当有功功率、无功功率的参考值发生变化后，系统可以迅速的调节，重新进入稳态大约需要0.3 s时间。通过两个图形的对比不难发现，整流换流器与逆变换流器的有功功率大小、走势几乎一致但方向相反，这是因为整流站从交流系统吸收功率，故有功功率为正，而逆变站向交流系统发出功率，故有功功率为负。在t=1.5 s处，整流器交流侧有功功率减少0.1 p.u，而整流站和逆变站的无功波动不大；同理，在t=2 s处，整流器交流侧无功功率减小0.1 p.u.，而两换流站的有功功率几乎没有发生变化，由此验证了VSC-HVDC系统可以独立的控制有功和无功功率。

实验总结：本实验通过对VSC-HVDC输电系统在稳态运行和各种参量变化的仿真验证了本次建模的合理性和有效性。仿真过程中VSCHVDC系统可以独立控制有功、无功功率的特性也得到了体现。

3.2 交流侧短路故障运行试验

电力系统在运行过程中由于外力破坏、绝缘老化、雷击、误操作、设计制造缺陷等原因往往会发生如短路、断线等故障。在系统短路时可能产生设备损坏、系统振荡甚至系统崩溃等严重后果。随着柔性直流输电技术的应用愈加广泛，研究VSC-HVDC系统在交流侧发生短路状况时的一系列反应对于降低供电事故的发生几率具有重要意义。

基于上述原因，现在在MATLAB/SIMULNK平台上搭建VSC-HVDC系统交流侧短路故障的模型如图12所示。与3.1中的模型不同的是，本模型在交流侧加入了三相故障模块，在三相故障模块中可以设置各种短路类型。如图17所示。

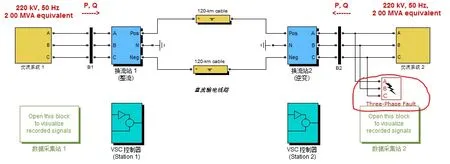
图12 VSC-HVDC系统交流侧短路模型结构图

单相接地短路是电力系统运行过程当中出现频率最高的短路故障。本实验在3.1的控制参数基础上对交流侧单相接地短路（以A相为例）进行模拟，故障接入时间：t=1.9 s,故障持续时间0.14，各相关物理量波形如图13。

图13（a）单相接地短路时整流站交流侧电压、电流波形

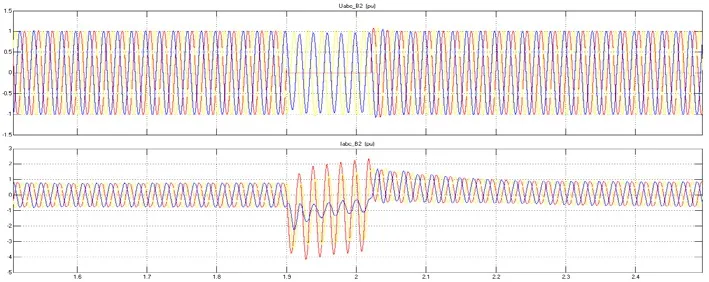
图13（b）单相接地短路时逆变站交流侧电压、电流波形

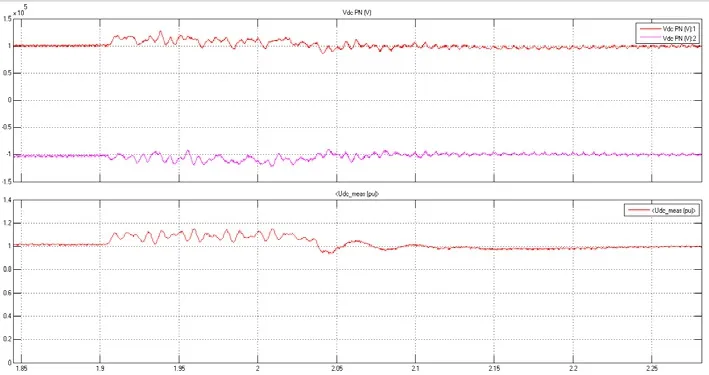
图14（a）单相接地短路时整流站直流侧电压

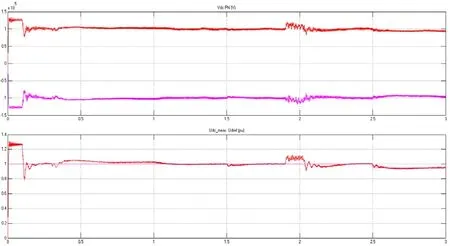
图14（b）单相接地短路时逆变站直流侧电压

波形分析：在t=1.9 s时，受端交流系统发生单相接地短路，逆变站的交流侧A电压瞬间降为0，A相电流也产生极大波动；而整流站的交流侧电压几乎没有发生变化，这是因为系统的整流端采用定直流电压控制，整流端直流电压不变，交流电压自然不发生变化。这也验证了VSC-HVDC系统在某种程度上可以起到故障隔离的作用，当一端交流系统发生小的扰动（在调节范围内的扰动）并不会影响另一端交流系统的正常运行，供电质量也不会受到影响。

波形分析：在t=1.9 s时，逆变换流站的交流侧发生A相接地短路，短路点产生很大的短路电流，导致整流站和逆变站直流侧的电压上升，由于控制环节的控制，直流电压被限制在可接受的范围内，短路解除后回归正常。

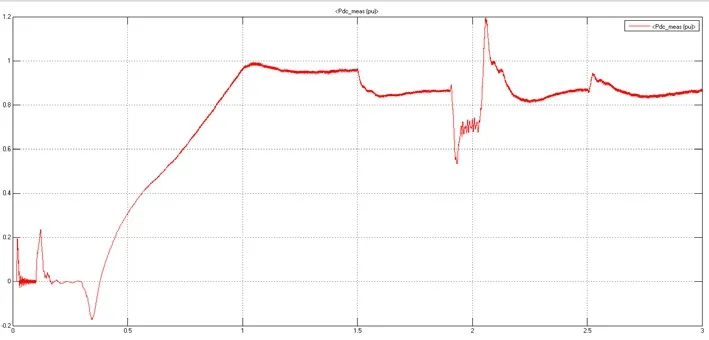
图15（a）单相接地短路时整流站直流侧有功功率波形

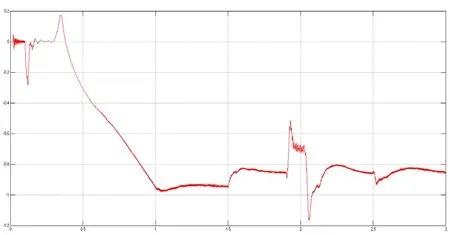
图15（b）单相接地短路时逆变站直流侧有功功率波形

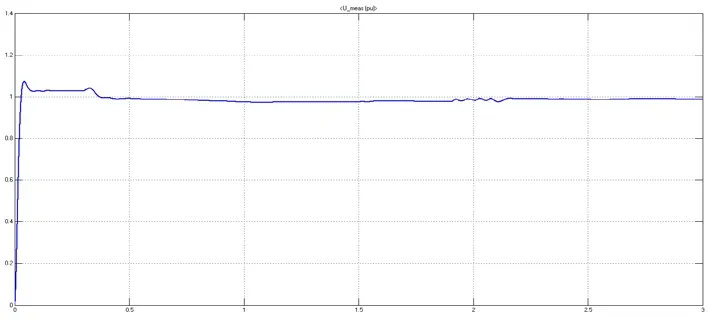
图16（a）单相接地短路时整流站交流侧电压（标幺值）

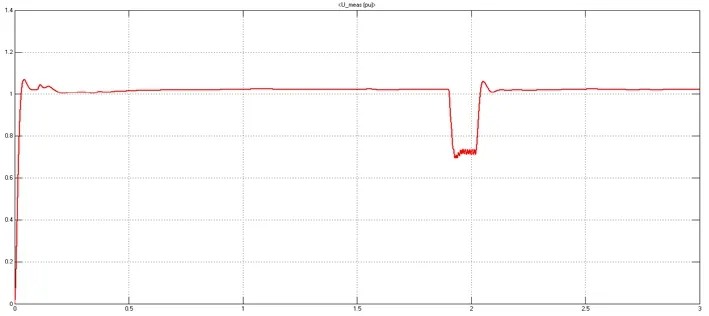
图16（b）逆变站交流侧电压（标幺值）

波形分析：在t=1.9 s时，逆变换流站的交流侧发生A相接地短路，整流站和逆变站直流侧的有功功率急剧下降，这是因为受电端的交流系统有一项发生短路，系统的功率输送能力降低，在故障解除后有功功率恢复正常。整流、逆变两侧有功功率波形相反是因为整流站从交流系统1吸收有功功率，而逆变站向交流系统2输送有功功率。

波形分析：在t=1.9 s时，逆变换流站的交流侧发生A相接地短路，短路点产生很大的短路电流，导致整流站交流侧的电压波动，短路解除后逐渐回归正常，之所以不产生大的波动是因为整流侧采用定直流电压控制，直流电压不变，故通过连接变压器相连的交流系统电压不会产生大的变化。由于短路发生在逆变站的交流侧，因此逆变站的交流电压急剧下降，在短路解除后逐渐回归正常。

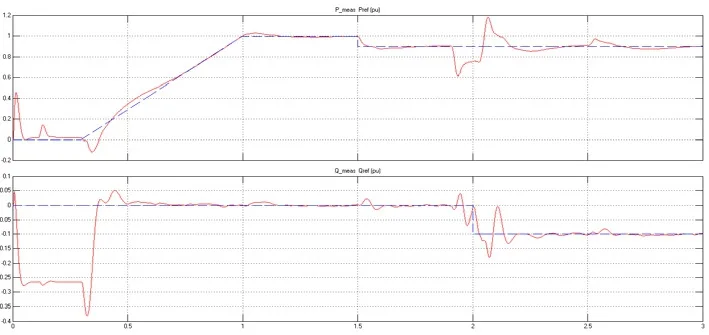
图17(a) 整流站交流侧有功无功参考值、测量值

图17(b) 逆变站交流侧有功无功参考值、测量值

波形分析：在t=1.9 s时，逆变换流站的交流侧发生A相接地短路，短路点产生很大的短路电流和一个短路压降，导致有功功率下降，控制系统为了使直流电压不发生大的变化，增加整流侧的无功功率输出以维持电压稳定。在t=2.0 s时整流站无功参考值降低0.1 p.u.，无功功率也相应下降，所以无功波形如图17(a)所示。同理，在短路发生时，控制系统控制逆变站向周围系统吸收无功功率以维持电压稳定，因此逆变站的无功功率测量值表现为急剧下降，短路解除后回归正常。