电动汽车有序充放电相关问题研究

邓志贤，兰玉清，陈进

（1.云南电网有限责任公司昆明供电局，昆明 650000；2.昆明云锗高新技术有限公司，昆明 650000）

0 前言

随着电动汽车推广，充电设施的建设也迫在眉睫，而对某区域充电负荷进行预测，就成了指导充电设施规划的基础。而在充电设施规划的基础上，又可以对电动汽车充电策略进行研究。只有在负荷预测的基础上有步骤地进行电动汽车充电设施建设，才能在推进电动汽车发展的同时提高充电设施的利用率和减小电网负荷峰谷差。

电动汽车对于能量的需求全部来源于电能。电能作为一种清洁能源，相比于直接燃烧一次能源，有着更高的能源利用率，同时，也避免了化石燃料燃烧所引起的二氧化碳、二氧化硫等温室气体的排放。目前，国内外学者已经提出了一些充电桩规划方案和电动汽车有序充电策略。包括将电动汽车充电过程参与系统频率调节、减少配电网损耗、降低峰值和低谷、抑制新能源输出波动等。

1 研究问题的提出

针对电动汽车的推广，需要对电动汽车充电设施进行合理的规划。文献[1]考虑电动汽车接入电网(V2G)技术作用，建立合理的电价机制，引导电动汽车用户在负荷高峰期合理有序地充放电，对充电站作为电源和负荷运行分别定义相应的运行权系数，用于计算配网综合运行成本。大部分是对充电站的选址问题、充电设施建设模式对于电网的影响、优化布局等进行研究。在此基础上，通过对充电站的合理规划，提高充电桩利用率，以降低充电设施建设成本为目标。

针对电动汽车对电网产生的影响，需要对电动汽车充电进行控制。文献[2]讨论了电动汽车荷载的随机性。通过负荷预测和轧制优化，提高了电动汽车有序充电的峰值填充效果。文献[3]分析了区域电网中的电动汽车如何与风电协调合作，减少负荷波动，使用动态规划方法解决负载波动问题。这些研究主要是让电动汽车充电过程参与系统频率调节、减少配电网损耗、降低峰值和低谷、抑制新能源输出波动等。因此需要研究以最小化系统等效负荷峰谷差为目标。达到节约电网运行和投资成本，提高设备利用率的目的。

因此，如何基于充电负荷预测结果对充电桩数量进行规划，如何在规划的基础上实现有序充电是目前研究的重点。

2 研究方案

以电动汽车充电设施规划以及充电策略的制定为目标进行研究。主要内容大致分为以下三部分：

1）对电动汽车行驶特性与分类，在行驶里程、出行次数、充电概率等因素进行了分析，根据这些影响因素的特性构造一个简单、适用的概率模型或随机模型，即利用蒙特卡洛法产生电动汽车充电起始时刻、充电时长等方面的数据。使问题的解对应于该模型中随机变量的某些特征（如概率、均值和方差等），所构造的模型在主要特征参量方面要与实际问题或系统相一致。基于这些特性利用蒙特卡洛法产生符合实际的随机数据，并利用MATLAB进行建模得到电动汽车充电负荷需求预测结果。

2）基于电动汽车充电负荷预测结果，以提高充电桩利用率、缩小充电站建设成本为目标采用PSO寻优算法对充电桩数量进行了规划，在实例的基础上进行了仿真，确定了区域内优化后充电桩的数量及建设成本，验证了本文所提出规划方法的有效性。

3）在充电桩规划结果的基础上，从电网角度出发，以负荷峰谷差最小从而降低调度成本为目标。依然采用PSO寻优算法，通过仿真结果分析制定了电动汽车充电策略并证明了该策略的可行性。

3 算例分析

3.1 场景介绍

在一个城区内，该区域主要包含了居民区、商场、写字楼三种不同功能的区域。而根据功能种类的不同，各区域所包含的电动汽车的用户种类也有所差别，同时在电动汽车充电行驶特性、充电特性等也有很大差别。比如，居民楼用户的充电时间大部分集中于夜晚，而写字楼用户则在白天集中充电，商场则一直人来人往，故其充电时间则比较分散，属于一直含有充电用户的类别。因此我们可以综合这几类因素以达到协调充电，完成提高充电效率的目的。区域规划图如图1。

其 中， 居 民 楼 为：A1、A2、A3、B1、D1、D2、D3；写字楼为：B3、C1、C3；商业区为：B2、C2。

图1 区域规划图

为节省充电区域占地面积及方便用户充电，计划在居民区B1，写字楼C3两处集中建设充电桩，而充电方式也采用常规充电方式，其充电功率为W=7 kW。根据电动汽车的行驶特性，在利用蒙特卡洛产生随机数据时，利用混合高斯分布对电动汽车的充电特性进行以下确定。具体参数设置如表1。

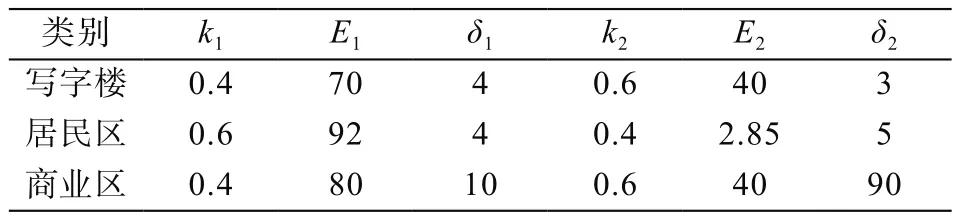
表1 混合高斯分布参数

表1中，k表示权重，E表示均值，δ表示方差。

3.2 电动汽车充电负荷需求预测

3.2.1 蒙特卡洛在本文中应用

针对三种不同区域用户，从用户数量、行驶特性、充电特性三个因素进行仿真，仿真数据则源于采集的实际充电特性结合蒙特卡洛法产生的随机数据。由蒙特卡洛法，根据概率模型的特点和随机变量的分布特性，设计和选取合适的抽样方法，并对每个随机变量进行抽样。按照所建立的模型进行仿真试验、计算，求出问题的随机解。根据充电时刻和日行驶里程数之间的数学关系，利用概率论中二维分布的相关知识最终得到概率密度分布，但在进行仿真时发现该概率密度函数表达式为含参数的定积分，不易产生随机数，因此先求出充电电能，最后计算充电时间常数的方法，从而避免了充电时间复杂的表达式。采用Acceptance-Rejection Method 进行模拟。结果如图2所示。

图2 一天内各时刻单辆功率需求的期望与标准差

以上分析了在居民区无规划管理情况下一天内单辆电动汽车充电功率需求的数学模型，但实际情况是一天内有多辆汽车需要充电，由中心极限定理可知，在某一时刻假设有N辆汽车需要充电，只要N足够大，这N辆电动汽车的总体功率需求将呈现正态分布，并且其期望为，方差为。其中和分别是单辆车在这一时刻充电功率需求的期望和标准差，可由上述仿真结果求得。根据正态分布原则，我们可以将内这个区间作为置信区间来估计功率需求的上下限。在仿真中，取N=1000，则这1000辆汽车充电功率需求将如图2所示分布在两条线之间。从图2中还可以看出，汽车总体功率需求在19:30最大。

图3 写字楼负荷预测

3.2.2 负荷预测结果

在该模型内主要包含了居民区、商场、写字楼三种不同功能的区域。根据不同区域用户类型的不同，其电动汽车充电功率需求也有很大差异。

1）由写字楼大部分为上班族的特点，其充电时间普遍集中在白天。在一天内该区域电动汽车充电负荷特性预测结果如图3所示。

以下四个图为写字楼区域在不同数量（N）电动汽车下的充电负荷特性预测结果，横轴为时间T，令15 min为一个单位则一天时间可换算为96个单位时间，纵轴为该区域总充电功率需求。观察预测结果图可知用户数量仅影响负荷大小，并不会影响充电特性。在该区域电动汽车数量N=473时，由预测结果图可知极大功率需求数据为t=10:28 am，P=301.95 kW；t=18:00 pm，P=364.21 kW。

2）居民区充电时间集中于夜晚，可能在白天也存在少部分充电用户，但可以通过合理的提议让居民区用户将充电时间安排在夜晚，以便于平衡充电功率。在一天内该区域电动汽车充电负荷特性预测结果如图4所示。

以下四个图为居民区域在不同数量（N）电动汽车下的充电负荷特性预测结果，横轴为时间T，令15 min为一个单位则一天时间可换算为96个单位时间，纵轴为该区域总充电功率需求。在该区域电动汽车数量N=568时，由预测结果图可知极大功率需求数据为t=1:28 am，P=446.27 kW；t=23:15 pm，P=358.62 kW。分别对应的功率需求存在两个波峰的原因是电动汽车充电完成大约在5小时，可安排充电站管理人员通过合理的规划将电动汽车分为两批进行充电。

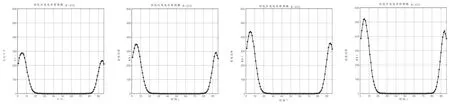
图4 居民区负荷预测

3）商业区的充电功率特性则比较稳定，因为在商业区营业期间会有不断来往的消费者，因此不会存在较大波动。在一天内该区域电动汽车充电负荷特性预测结果如图5所示。

图5 商业区负荷预测

以上四个图为商业区在不同数量（N）电动汽车下的充电负荷特性预测结果，横轴为时间T，令15 min为一个单位则一天时间可换算为96个单位时间，纵轴为该区域总充电功率需求。在消费高峰期会存在一定的峰值。在该区域电动汽车数量N=710时，由预测结果图可知极大功率需求数据为t=11:15 am，P=167.34 kW；t=19:25 pm，P=229.73 kW。虽然商业区的流动车辆比较多，但由于去商场的电动汽车用户大部分是就餐、购物、娱乐等原因，停留时间一般不会超过两小时，因此绝大部分用户不会对车辆进行充电。

3.3 电动汽车充电桩数量规划

3.3.1 PSO寻优算法在充电桩规划应用

本模型中需要建设两个充电站，因此也涉及到优化方面问题，根据粒子群改进算法对两个充电站的充电桩数量进行优化。从而达到优化设计的目的。采用的改进算法的改进方面是随机权重策略，即随机地选取ω值，使得微粒历史速度对当前速度的影响是随机的，为服从某种随机分布的随机数，从一定程度上可从两方面克服ω的线性递减带来的不足。首先，如果在进化初期接近最好点，随机ω可能产生相对较好的ω值，加快算法的收敛速度。另外，如果在算法初期找不到最优点，ω的线性递减，使得算法最终收敛不到此最好点，而ω的随机生成可以克服此局限。ω的计算公式如下：

在公式1中，N（0,1）表示标准正态分布的随机数，rand(0,1)表示0到1之间的随机数。研究表明，随机权重策略的PSO算法对于多峰函数，能在一定程度上避免陷于局部最优，该方法多用于动态系统中。

3.3.2 充电桩优化结果

优化目标：充电站建设成本

公式2中，C为优化后两个充电站的建设总成本；N为两个充电站建设充电桩总数；N1为居民区B1处充电站充电桩数目，在B1充电站处原有10个充电桩，且根据空间条件最多能在该点建设100个充电桩，因此10≤N1≤100；N2为写字楼C3处充电站充电桩数目，在C3充电站处原有16个充电桩，且根据空间条件最多能在该点建设80个充电桩，因此16≤N2≤80；P1、P2为两个充电站充电桩的单个建设成本，P1=1.84万元、P2=2.17万元；a、b为充电桩价格波动系数，会跟随N1、N2变化，具体情况如表2所示。

表2 价格波动系数

在优化计算过程中，保留一定裕度，设置裕度k=1.1。通过随机权重策略的粒子群算法寻优计算之后得到结果，在B1居民楼电动汽车充电站需建设充电桩数量N1=54个，在C3写字楼电动汽车充电站需建设充电桩数量N2=37个，两个充电站的优化成本为C=172.464万元。

在充电桩数量优化后将写字楼、居民区、商业区三块区域的预测充电功率进行叠加，得到该模型内的预测功率需求总和。模型中电动汽车充电负荷特性总和预测结果如图6所示。

其中，横轴为时间t，令15 min为一个单位，则一天时间可换算为96个单位时间，纵轴为该区域总充电功率需求。在该封闭模型中电动汽车充电负荷特性总和预测图中，最大需求功率为Pmax=576.436 kW，时间t=72、即区域最大功率需求时间出现在晚上六点。

3.4 有序充电策略

3.4.1 PSO寻优算法在有序充电应用

在研究电动汽车有序充电过程中依然采用粒子群改进算法进行优化，从而实现最小化系统等效负荷峰谷差的目的。且依然采用随机权重策略的PSO改进算法。

3.4.2 有序充电优化结果

1）有序充电的主要是为了实现最小化系统等效负荷峰谷差，达到节约电网运行和投资成本，提高设备利用率的目的优化目的。减小负荷的峰谷差是指减小某区域的日负荷峰谷差，这就需要在该区域日负荷曲线的基础上，去寻找限定条件下最优的充电策略。在3.1节所介绍的场景下设置有473辆电动汽车情况下，按照常规负荷情况对该区域进行日负荷预测。其日负荷曲线如图7所示。

图6 负荷预测总和

该曲线是通过对某城区的日负荷结果进行统计并结合设计场景而得，得到的初始曲线是一个波动频率较高的锯齿形曲线，通过高斯变换之后将其变为一条光滑的曲线。从该日负荷曲线中可以得知，该区域最大日负荷点出现在t=18:24 pm，此时P=7668.6763 kW，而最小负荷点出现在t=6:21 pm，此时P=4547.5409 kW。

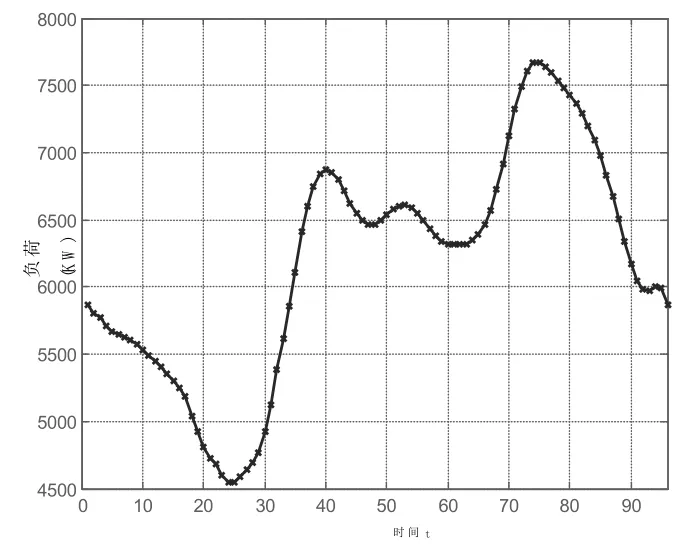
图7 日负荷曲线

2）通过PSO寻优算法得到电动汽车有序充电的功率需求总和，在一天内该模型中电动汽车充电负荷特性总和预测结果如图8所示。

其中，横轴为时间t，令15 min为一个单位，则一天时间可换算为96个单位时间，纵轴为该区域总充电功率需求。在该封闭模型中电动汽车充电负荷特性总和预测图中，优化前最大需求功率为Pmax=576.436 kW，时间t=72、即区域最大功率需求时间出现在晚上六点，优化后Pmax=368.578 kW。

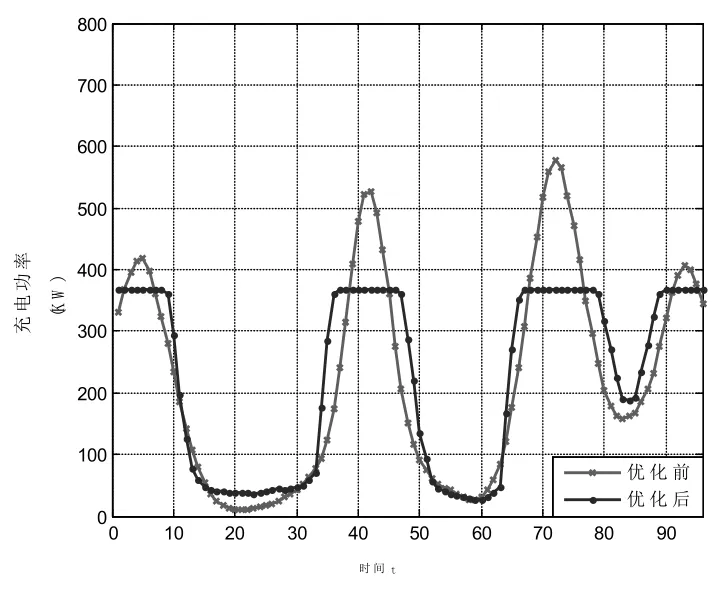
图8 优化前后负荷预测结果

3）在得到该场景内日负荷曲线的情况下，我们可以在此基础上加入电动汽车无序充电和有序充电的情况。具体情况如图9所示。

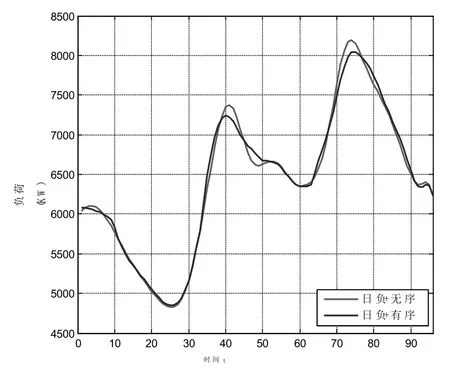
图9 有序充电前后日负荷曲线

在图9中，红色曲线是电动汽车进行无序充电情况下该区域的日负荷情况，蓝色曲线是电动汽车在有序充电情况下该区域的日负荷情况。可以看出，有序充电情况下抑制负荷峰谷差效果并不是很明显，这是由于电动汽车充电负荷相对于该区域总负荷而言占比很小的原因。但是也可以看出在有序充电情况下日负荷曲线变得更加平缓，波动更小。在8:24 am至第二天凌晨2:48 am可以看到明显的优化效果，而在另一时间段由于电动汽车充电负荷需求较小，则优化效果较小。两条曲线的总电量都为W=158 843.28 kW.h，Pav=66 18.47 kW，电动汽车的有序充电使负荷峰值从无序时的8217.6 kW下降到8042.9 kW，下降了174.7 kW；负荷峰值从无序时的4796.2 kW上升到4817.6 kW，上升了21.4 kW。从负荷整体趋势上着眼，有序充电方式使配电网的峰谷差率从初始的41.6%下降至40.1%，一定程度上平抑了配电网的负荷波动，减小了负荷峰谷差，改善了负荷特性。采用本文提出的双层模型充电方案，电动汽车通过在峰荷时放电缓解了电网的调峰压为，减少了电网运行的备用容量，提高了系统运行的可靠性和经济性。两种不同的充电方式情况下，电动汽车对该区域总负荷的影响情况如表3。

表3 不同充电方式下电网负荷的峰谷差

根据表格中的优化计算数据可以看出在有序充电情况下负荷峰谷差得到了明显改善。而在抑制负荷波动方面有序充电较无序充电而言有明显改善。

3.5 小结

本章首先对算例的场景进行了一定的介绍，对其中的一些条件因素进行限制规定；而后，基于电动汽车行驶特性（行驶里程、出行次数、充电概率）对电动汽车充电负荷进行了预测；然后，基于电动汽车充电负荷预测结果，采用PSO寻优算法对充电桩数量进行了规划；最后，在规划结果的基础上，从电网角度出发，以负荷峰谷差最小为目标，制定了电动汽车充电策略。仿真结果验证了本文所提出规划方法以及充电策略的有效性。

4 结束语

为了提高电动汽车充电桩效率，节约成本，引导用户进行有序充电，本文建立了一种基于改进粒子群算法的电动汽车有序充电控制模型，充分考虑了电动汽车的运行特性、充电特性，将模型解耦为基于时间尺度优化调度子模型。算例表明，该模型可以实现24小时实时电动汽车充电优化控制，实现提高充电桩效率和激励用户有序充电的双重优化目标。具体的研究成果总结如下：

1）大规模电动汽车的无序充电行为会对电网运行带来许多挑战，本文首先研究了电动汽车的充电负荷特性和负荷建模，而电动汽车的充电负荷特性主要受汽车保有量、汽车充电方式、开始充电时间、充电功率、充电时长和充电频率等因素影响，在蒙特卡洛法概率抽样的基础上，计算规模化电动汽车的充电负荷需求量，然后通过改进PSO算法得到在设计场景中的充电桩数量最优解，最终降低充电功率峰值差，从而实现提高电动汽车充电桩效率的目标。

2）电动汽车作为一种良好的需求侧响应资源，本文在研究电动汽车有序充电时考虑了在安全约束的条件下，首先根据电动汽车充电负荷预测结果对充电桩进行了规划，然后在充电桩规划结果的基础上构建了合理的有序充电模型，通过在不同时刻调度电动汽车合理接入到节点实现了电动汽车充电功率优化，最后通过改进PSO算法得到最优解，实现最小化系统等效负荷峰谷差，达到节约电网运行和投资成本，提高设备利用率的优化目的。