质量和成本约束下CSP-T和Spk集成过程控制方案

李春芝，甘卫华，鄢伟安

(1.华东交通大学 交通运输与物流学院；2.过程控制与可靠性研究所，江西 南昌 330013)

自动控制和信息技术的发展与应用，极大提高了制造企业的加工能力，使得生产能力稳定，工序任务能够快速且全自动地被完成。节奏快速和能力稳定的自动化车间，任意一台设备的故障都可能导致整个车间停产，需要严密监控设备运行。监控手段是利用监测设备收集加工数据，利用信息系统和数据挖掘技术分析加工数据。监控目的是保障加工过程稳定在设计许可的能力水平和质量水平。实现过程监测，需要制定合理的过程控制方案，以全面完成各项监测任务。以过程控制方案为原型，构建快速响应的数据挖掘系统，通过数据挖掘技术，发现过程波动趋势信息，将信息及时反馈给控制系统，控制系统及时调整控制参数以保障加工过程的能力水平和质量水平满足设计需求[1]。

自动化车间过程控制需要同时满足质量、成本、风险等多项约束。顾客质量需求形成质量约束，生产运行需要的成本构成成本约束。为同时满足质量和成本约束，对过程状态判断的风险控制形成风险约束。多项约束需求要求过程控制方案具备及时采集过程数据、监测过程状态、进行数据分析和实时反馈等多项功能[1]。现行过程控制方法，包括连续抽样检验(continuous sampling plan，CSP)[2]、过程良率指数[3]、过程能力指数[4]、过程合格品率[4]、设备维护[5-6]、控制图[7]等，都不能同时达成以上功能需求。

多水平连续抽样方案(CSP-T)是过程质量控制方案[2]。CSP-T从连续检验开始，当连续合格品数达到规定的数量，即转到分数检验，当分数检验阶段的连续合格品数达到规定的数量，可根据规则降低检验分数，分数检验阶段一旦遇到不合格品，则立即返回全检。CSP-T在平均检出质量极限等值面上选择检验方案，无论过程质量改善或者恶化，都可以确保过程质量满足质量需求。但CSP-T方案只能满足质量约束，不能满足成本约束。

为建立满足成本约束的CSP-T方案，很多学者从经济性角度研究了CSP-T方案的属性。Cassady等[8]在考虑检验成本、返修成本和接收成本的基础上，证明了CSP系列方案对于过程控制是不经济的，过程控制应该要么全检要么不检。但研究没有给出全检或者不检的分界过程状态。Haji等[9]将成本划分为检验成本、返修成本和退回成本，推断出要么全检要么分数检验的结论。Eleftheriou等[10]则将成本视为内部成本和外部成本，外部成本用损失函数进行核算，建立了基于总成本最小的CSP方案参数求解模型。由于采用不同的成本分类方式，研究者得出CSP成本优化的不同结论，因此无法建立一致的成本最低的CSP方案参数优化方法。

学者们探讨了同时满足质量约束和成本约束的最优CSP方案。但至今没有对CSP运行的最低成本点达成共识。为建立同时满足成本约束和最优维护策略的集成过程控制方案，Bouslah等[11]提出预防性维修(preventive maintenance，PM)与CSP集成过程控制方案。这些研究以成本局部最优为优化目标，根据效益悖反理论，生产过程的局部项目成本最小可能导致产品总成本的提高。Li等[12]提出由过程能力和质量约束同时决定的最优连续抽样检验方案。但是，该方案不适应给定检验能力下的过程控制方案制定。在既定制造资源下，最大化发挥现有生产能力，是过程控制方案的任务和应该达成的目标。

CSP-T方案的另一个缺陷是第一类和第二类风险都很高且无法同时得到控制。Wu等[13]提出了基于过程良率指数Spk估计的批量产品质量检验方案，该方案利用Spk估计的精确分布建立能够同时控制两类风险的检验方案。Spk估计的精确分布是近似的正态分布，是Lee等[14]依据Spk估计的一阶泰勒展开的属性建立的。Spk与过程合格品率是一一对应关系[15]。判定批次产品质量或过程质量水平时，目前的检验方案和质量控制方案，均不能同时控制两类风险。Wu利用过程能力指数估计量的分布密度函数，制定了能同时控制两类风险的组批产品质量控制策略。Wu的风险控制思路显然可以拓展应用于在线过程的风险控制。建立质量和成本约束下，基于过程良率指数Spk估计量精确分布的同时满足两类风险的过程控制策略，是稳态过程控制亟待解决的问题。

由此提出满足质量约束、成本约束、第一类和第二类风险共4种约束的CSP-T和Spk集成过程控制方案。集成控制方案利用受控过程的统计稳定性特征，建立质量约束和成本约束与过程状态的对应关系，找到满足质量和成本约束的最优CSP-T方案，构建基于Spk精确分布的风险控制方案满足控制过程波动的风险控制需求。

1 过程控制需求分析和约束变量生成

1.1 过程控制需求分析

自动化产线一般由受控过程构成。受控过程的过程控制需求可以细化如下。

1) 确定过程控制的质量约束和成本约束。

2) 定量表达过程状态。

3) 判定过程状态的能力水平和质量水平：对于不能满足质量和成本约束的过程，终止生产；为能够满足质量和成本约束的过程制定集成过程控制方案。

4) 运行过程控制方案，实时监测过程状态，确保过程控制能够同时满足质量和成本约束需求。

过程控制中的两类风险，第一类风险指高质量水平过程被误判为低质量水平的风险。第二类风险指低质量水平过程被误判为高质量水平的风险。过程良率指标(process yield index，Spk)对于在线过程控制具备以下优势：既能体现过程能力，又能反映过程稳定性，同时和过程合格品率(process conformance，pc)是一一对应关系。CSP-T是多水平连续抽样检验方案，通过分数检验阶段降低检验分数实现对较好质量过程的放宽检验。

1.2 约束变量

质量约束是过程控制需要满足的首要目标。平均检出质量极限(average outgoing quality limit，A OQL)是CSP-T需要满足的质量约束，也是集成过程控制方案的质量约束变量。

过程控制方案的运行目的是在既定制造资源下，以最小的检验工作量满足各项约束需求。CSP-T方案的性能指标长期平均检验数(average fraction inspected，A FI)体现了方案运行形成的检验工作量。成本约束是为保障工序质量生产过程能够承担的最大检验工作量，该最大检验工作量可视为长期平均检验数极限，记为 AFIL。当过程状态处于需要用最大检验工作量才能满足质量约束的时候，称处于该状态的过程为极限过程。极限过程的过程不合格品率记为pIQL，称为极限过程质量。极限过程下(p=pIQL) (p是过程不合格品率)，AOQ=AOQL 和AFI=AFIL同时成立，AOQ(average outgoing quality)是CSP-T的平均检出质量。极限过程下，由关系式AFI=1−AOQ/p，得到AFIL=1−AOQL/pIQL。该关系式表明，对于pIQL＜AOQL的过程，AFIL＜0，表明过程质量能够满足质量约束，不需要运行过程控制方案；对于pIQL＞AOQL的过程，AFIL＞0，过程质量相比于过程质量需求偏低，需要运行过程控制方案进行过程控制。AFIL为集成控制方案的成本约束变量，AOQL既是质量约束变量，也是过程状态控制阈值。

以高概率接收高质量水平过程(p≤AOQL)，即L(p≤AOQL)≥1−α；以低概率接收低质量水平过程(p≥pIQL)，L(p≥pIQL)≤β 。α、β是 风险约束。α是拒收高质量过程的概率，称为第一类风险； β是接收低质量过程的概率，称为第二类风险。

2 CSP-T和Spk集成过程控制方案

2.1 同时满足质量和成本约束的CSP-T检验方案

CSP-T方案的AOQ和AFI绩效公式为

其中，i是连续检验阶段的连续合格品数，f是分数检验阶段的初始检验分数。

既定检验方案 (i,f)满足质量约束和成本约束的能力可以表示为如下不等式：

根据CSP-T检验方案的制定方法，所有满足质量约束A OQL的AOQL等值面方案(i,f)，均有AOQ(i,f,pc)≤AOQL。因此，所有AOQL等值面方案都能使得式(3)成立。能够满足成本约束的检验方案必然存在于 AOQL等值面方案中。因此，需要分析AOQL等值面方案满足成本约束的情况。

极限过程(p=pIQL)是成本约束下恰好能得到合格质量的受控过程。极限过程下将AOQL等值面方案分为3类，分别是pL＜pIQL，pL=pIQL和pL＞pIQL的AOQL等值面方案。pL＜pIQL和pL＞pIQL的AOQL等值面方案有无穷多个，pL=pIQL的AOQL等值面方案只有1个。pL是特殊的p值点，当p=pL时，AOQ曲 线的AOQ=AOQL=max(AOQ)。图1(a)是3类 AOQL等值面方案的AOQ曲线，图1(b)是3类A OQL等值面方案的AFI曲线。图1(a)显示，3类AOQL等值面方案在pc的值域范围内都能满足质量约束 AOQ≤AOQL。图1(b)显示，pL＜pIQL和pL＞pIQL的AOQL等值面方案，当p≤pIQL时，在p左边的部分区域存在 AFI＞AFIL，不能满足成本约束AFI≤AFIL。只有pL=pIQL的 AOQL等值面方案在p≤pIQL时能满足成本约束A FI≤AFIL。因此，pL=pIQL的A OQL等值面方案是唯一能够满足质量和成本约束的CSP-T方案，将其记为(iIQL,fIQL)。

同时满足不等式(3)和(4)的唯一解 (iIQL,fIQL)是同时满足质量约束 AOQL和 成本约束 AFIL的唯一可行AOQL等 值面方案。pL=pIQL时，(iIQL,fIQL)方案参数求解公式为[16]

其中，pcIQL是极限过程的过程合格品率，pcIQL=1−pIQL。

表1给出了3个质量约束变量AOQL，每个AOQL有8个成本约束变量 AFIL的情况下，能够同时满足2种约束的CSP-T控制方案。从表1数据可知，相同成本约束AFIL下，随着质量约束AOQL增大，iIQL和fIQL都减小；相同质量约束AOQL下，随着成本约束(AFIL)降低，iIQL增大，fIQL减小；极限过程pIQL的值随着成本约束(A FIL)的降低而减小；质量约束A OQL、成本约束(A FIL)和检验方案 (iIQL,fIQL)之间是一一对应关系。利用式(5)和(6)可计算得出任意质量约束和成本约束组合下的CSP-T控制方案参数。

图1 同时满足质量约束和成本约束的CSP-T方案的性能曲线Figure 1 The performance curve of the CSP-T plan under the quality and cost constraints

2.2 基于过程良率的风险控制方案

过程良率指数(Spk)是Boyles[3]提出的过程能力指标，其表达式如下

其中，Φ(·)是标准正态分布函数，Φ−1(·)是其反函数，µ是过程均值，σ是过程方差，USL是上标准限，LSL是下标准限。

Spk与p一一对应[3]：

一般用样本均值估计µ，用样本方差s估计是样本量。则Spk的自然估计为

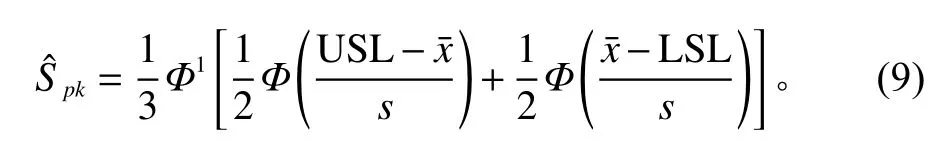
pk是复杂统计量，很难求得其累积分布函数。Lee等[14]将进行泰勒展开，得到的一阶近似

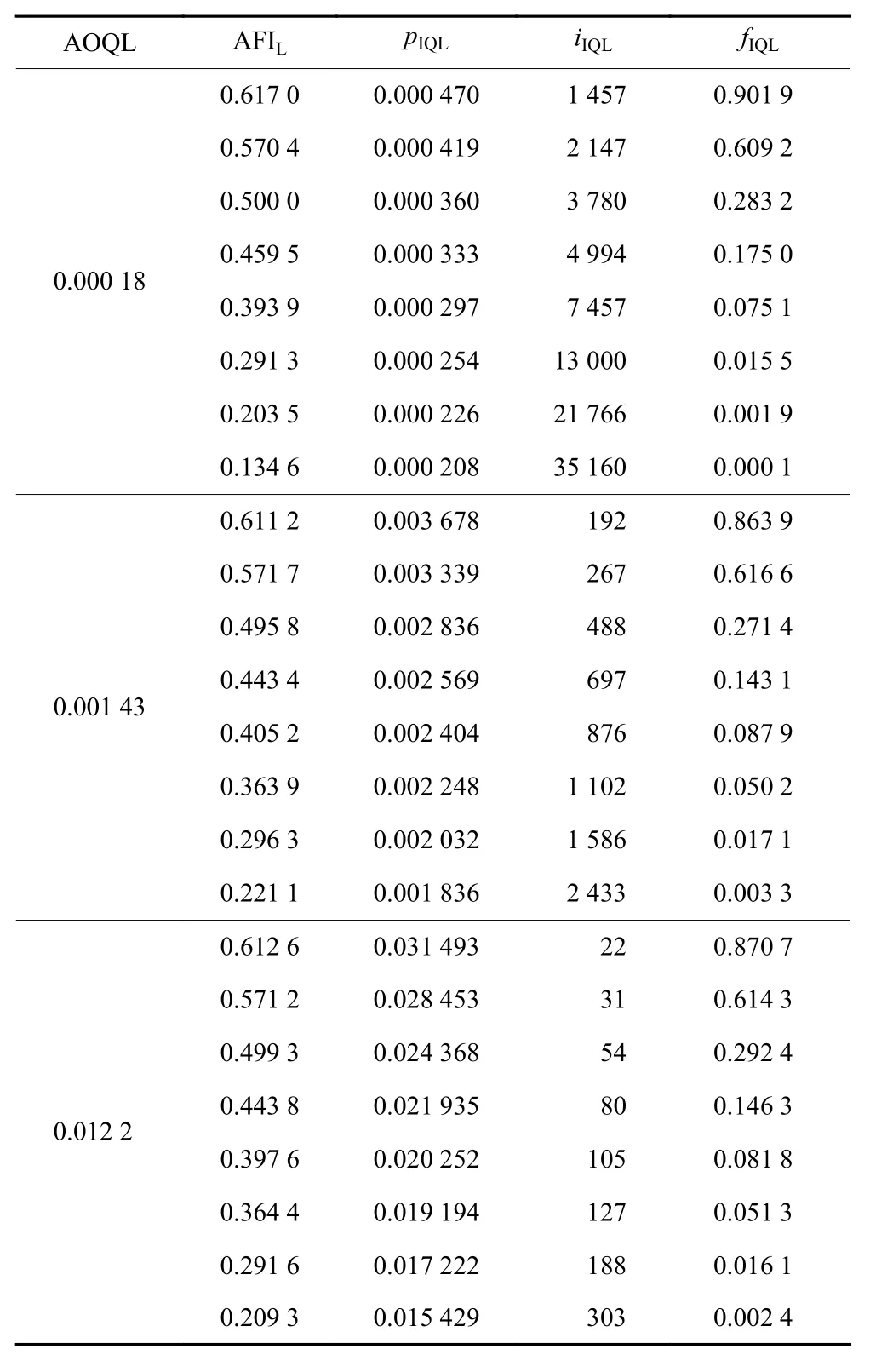
表1 满足质量约束AOQL和成本约束AFIL的CSP-T检验方案(iIQL，fIQL)Table 1 The inspection scheme (iIQL，fIQL) in CSP-T under the quality constraint AOQL and the cost constraint AFIL

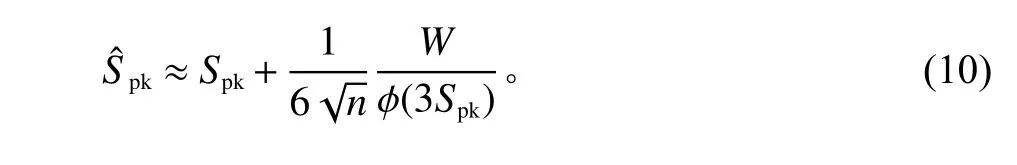
ϕ为标准正态分布下的概率密度函数。

M=(USL+LSL)/2。a和b都是µ和σ的函数

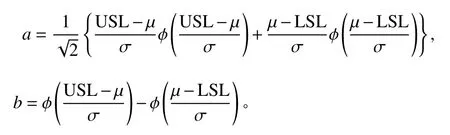
W是a、b、µ、σ、n、和s的函数。

Lee等[14]证明得到近似服从正态分布则概率密度函数为

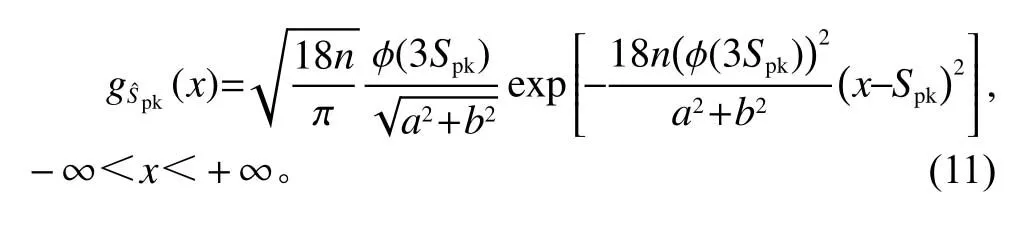
特定正态过程的过程良率指数视为常数S′，由式(7)可得其基于的正态分布的OC函数

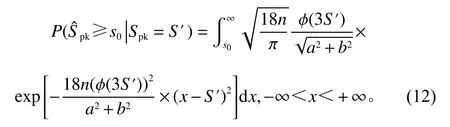
未知量s0是风险控制中过程良率指数的关键值。根据Spk与pc之 间的一一对应关系，p=AOQL的受控过程，其过程良率指数为SAOQL；p=pIQL的受控过程，其过程良率指数为SIQL。则风险约束需求(AOQL,α)和 (pIQL,β)，可以转化为 (SAOQL,α)和 (SIQL,β)，由式(8)得到两个风险控制不等式

s0是能够同时满足两类风险的过程良率指数的关键值。

式(13)和(14)的边界条件记为

将包含s0和n的等式(15)和(16)记为如下两个函数

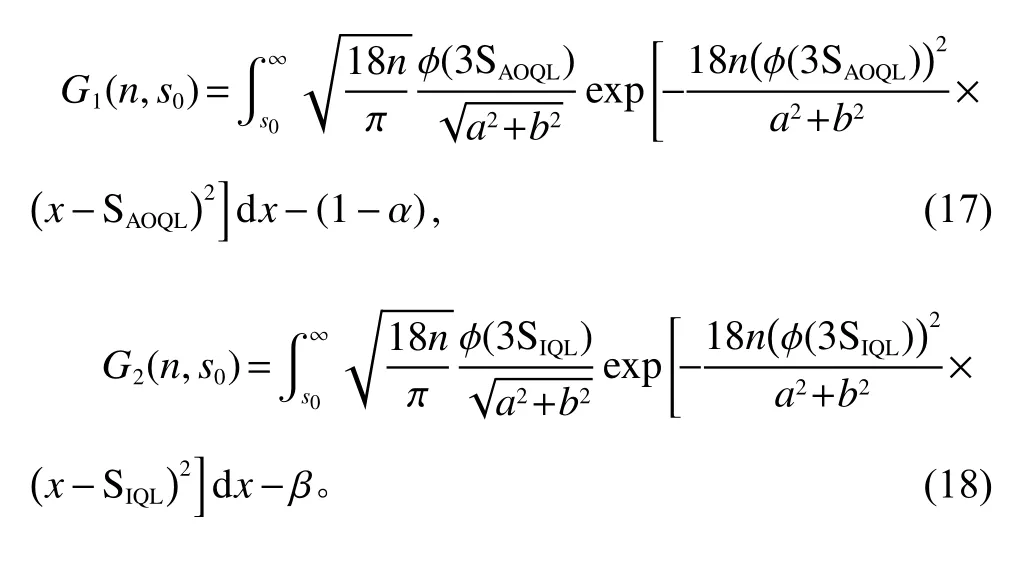
图2为G1和G2的曲面图。从图2可以看出，两曲面图在任意风险水平相交时，交点只有1个，说明式(15)和(16)有唯一共同解，即对于给定的质量约束和成本约束，同时满足两类风险的风险控制方案(n,s0)是唯一的。(n,s0)即为风险控制方案的控制参数。风险控制方案的运行模式为：连续收集n个加工数据，用加工数据求解pk，作出如下判断：pk＞s0，生产和检验继续进行；否则，说明过程状态不能同时满足质量和成本约束，应该终止生产。

显然，质量约束(AOQL)、成本约束(A FIL)、第一类风险 (α) 、第二类风险 (β)与 风险控制参数(n,s0)之间一一对应。

2.3 集成控制方案运作程序

质量控制方案 (iIQL,fIQL)依赖连续检验和分数检验的自适应调节，以成本约束能承担的检验数满足质量约束需求，但质量控制方案无法做到将过程波动风险控制在既定风险水平。风险控制方案(n,s0)以一定的风险(α，β)分别满足质量约束 AOQL和成本约束 AFIL，对过程波动进行控制，与质量控制方案优势互补，实现了两类风险的量化控制。4类约束(AOQL、AFIL、α和β)和4个方案参数(iIQL、fIQL、n和s0)之间是一一对应关系。过程合格品率估计和风险控制方案参数都可以用运行CSP-T方案时得到的加工数据进行计算，因此，集成控制方案相比于原来的CSP-T控制方案，检验工作量没有增加。集成方案(iIQL,fIQL,n,s0)的控制程序如下。

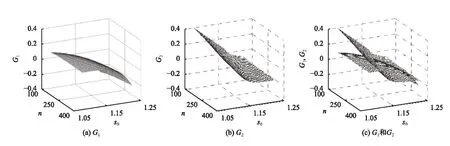
图2 曲面图Figure 2 The curved surface

Step 1 按CSP-T运作流程执行质量控制方案(iIQL,fIQL)；

Step 2 保持最新n个连续加工数据的记录，用n个加工数据计算

从运作流程可知，集成控制方案运行时，加工数据的计数特征驱动质量控制方案运行，加工数据的计量特征驱动风险控制方案运行。在不增加检验工作量的前提下，集成控制方案实现了过程状态监测、满足4类约束和反馈控制等多项控制功能需求。

3 分析和比较

表2 质量约束AOQL = 0.000 18(SAOQL= 1.248 5)时的集成控制方案Table 2 The integrating control scheme under quality constraint AOQL = 0.000 18(SAOQL= 1.248 5)

质量约束、成本约束和风险约束与集成控制方案的4个控制参数之间是一一对应关系。表2–4分别给出3个质量约束的取值，每个质量约束有3个成本约束的取值，以及与3种风险约束取值组合下的集成控制方案参数。其中，表2质量约束取值SAOQL=1.248 5 (AOQL=0.000 18)时，成 本 约 束 取 值SIQL=1.219 4，1 .206 0，1 .165 8，分别对应极限检验能力(AFIL=0.203 5, 0.291 3, 0.570 4)。表3质量约束取值SAOQL=1.062 8 (AOQL=0.001 43) 时，成 本 约 束 取 值SIQL=1.028 5，1 .018 4，0.978 2，分别对应极限检验能力 (AFIL=0.298 3， 0.363 9,0.571 7)。表4质 量 约 束取值SAOQL=0.835 4(AOQL=0.012 2)时，成本约束取值SIQL=0.794 0，0.730 3， 0.780 6，分别对应极限检验能力(AFIL=0.291 6，0.364 4，0.571 2)。风险约束分别为：α=0.03, 0.06, 0.09 ； β=0.03, 0.06, 0.09。由表2–4可知，随着质量约束 AOQL增大，3个方案参数iIQL、n和s0同时降低。fIQL由受控过程的过程能力和质量需求共同决定。质量需求 AOQL一定时，随着成本约束 AFIL的增大，iIQL、n和s0同时降低，fIQL增大。质量约束AOQL和成本约束 AFIL一定时，iIQL和fIQL有唯一最优方案，n和s0随着风险约束 α或/和β的增大同时减小。

表3 质量约束SAOQL=1.062 8 (AOQL = 0.001 43)时的集成控制方案Table 3 The integrating control scheme under quality constraint SAOQL=1.062 8 (AOQL = 0.001 43)

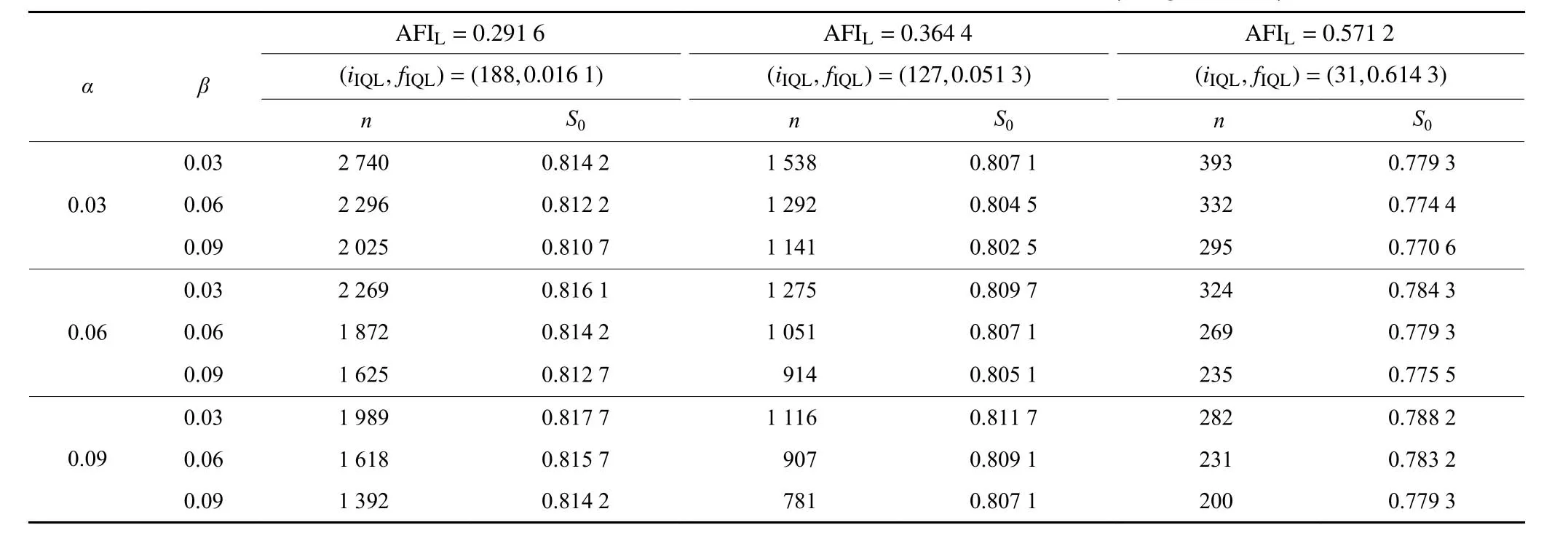
表4 质量约束SAOQL=0.835 4 (AOQL=0.012 2)时的集成控制方案Table 4 The integrating control scheme under quality constraint SAOQL=0.835 4 (AOQL=0.012 2)

根据表2−4的取值，图3−5分别给出集成控制方案与两个CSP-T方案的OC曲线。分析图3−5可知，4类约束 (AOQL,AFIL,α,β)的各种组合下，OC曲线较理想的都是集成控制方案。各种质量需求下，随着成本约束增大，集成控制方案的OC曲线向右移动。从曲线形状可见，集成控制方案的OC曲线斜率大，几乎接近理想的OC曲线。第一类和第二类风险在集成控制方案中都能够得到控制。而CSPT方案的OC曲线，两类风险都很高。

4 应用实例

阀板是空调外机外罩组件之一，经冲压成型，与外机内部零部件之间用螺栓装配。阀板上共有9个装配孔，都是冲压而成。为保障冲压质量一致性，需要对每个孔进行在线质量检验。质量需求AOQL规定为0 .012 2。原有在线检验方案是CSP-T的(i,f)=(37,0.5)。该在线检验方案不能及时判断过程状态，导致较大的第一类和第二类风险。拟用集成控制方案进行过程控制。以ϕ1 2.1±0.2 mm孔为例进行检验方案改善。对冲孔工序进行成本分析，得到工序能够承担的长期平均检验数极限AFIL=0.571 2。管理者将两类风险规定为α=0.03，β=0.09。查表4，可知同时满足4项约束的CSP-T与Spk集成控制方案为(iIQL,fIQL,n,s0)=(31, 0.614 3, 295, 0.770 6)。

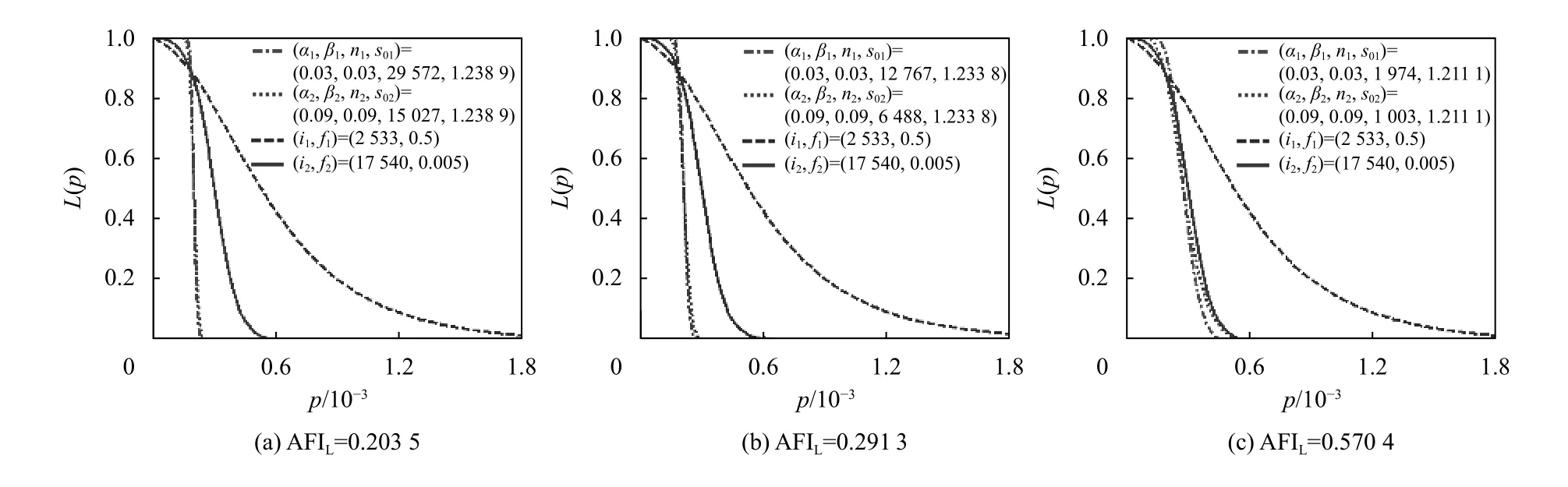
图3 质量约束AOQL = 0.000 18和3种成本约束下CSP-T和集成控制方案的OC曲线比较Figure 3 Comparison on the OC curves between CSP-T and the integrating control scheme under the quality constraint AOQL = 0.000 18 and three cost constraints

图4 质量约束AOQL = 0.001 43和3种成本约束下CSP-T和集成控制方案的OC曲线比较Figure 4 Comparison on the OC curves between CSP-T and the integrating control scheme under the quality constraint AOQL = 0.001 43 and three cost constraints

图5 质量约束AOQL = 0.012 2和3种成本约束下CSP-T和集成控制方案的OC曲线比较Figure 5 Comparison on the OC curves between CSP-T and the integrating control scheme under the quality constraint AOQL = 0.012 2 and three cost constraints

执行CSP-T方案 (iIQL,fIQL)=(31, 0.614 3)，连续收集 295个检验数据，并将数据列入表5。图6为数据的正态概率图。图7为数据的柱状拟合图。由图6和7可知，数据近似服从正态分布，且经过Matlab计算检验数据的Pvalue=0.648 9＞0.05，该过程为受控过程。

计算295个数据，可得样本均值=12.099 763，样本标准差s=0.085 752，过程良率指数估计值pk=0.778 8。显然，pk=0.778 8＞s0=0.770 6。该冲压工序可用集成控制方案进行过程质量控制。表6比较了集成控制方案与CSP-T方案的性能指标AFI、AOQ和接受概率。执行集成控制方案后，过程质量改善，AOQ降低0.000 192。应用基于过程良率的风险控制方案进行风险控制，接受概率得到提高，本冲压工序的接收概率提高了 0.020 705。在检验能力极限的约束下，AFI提高0.009 859。

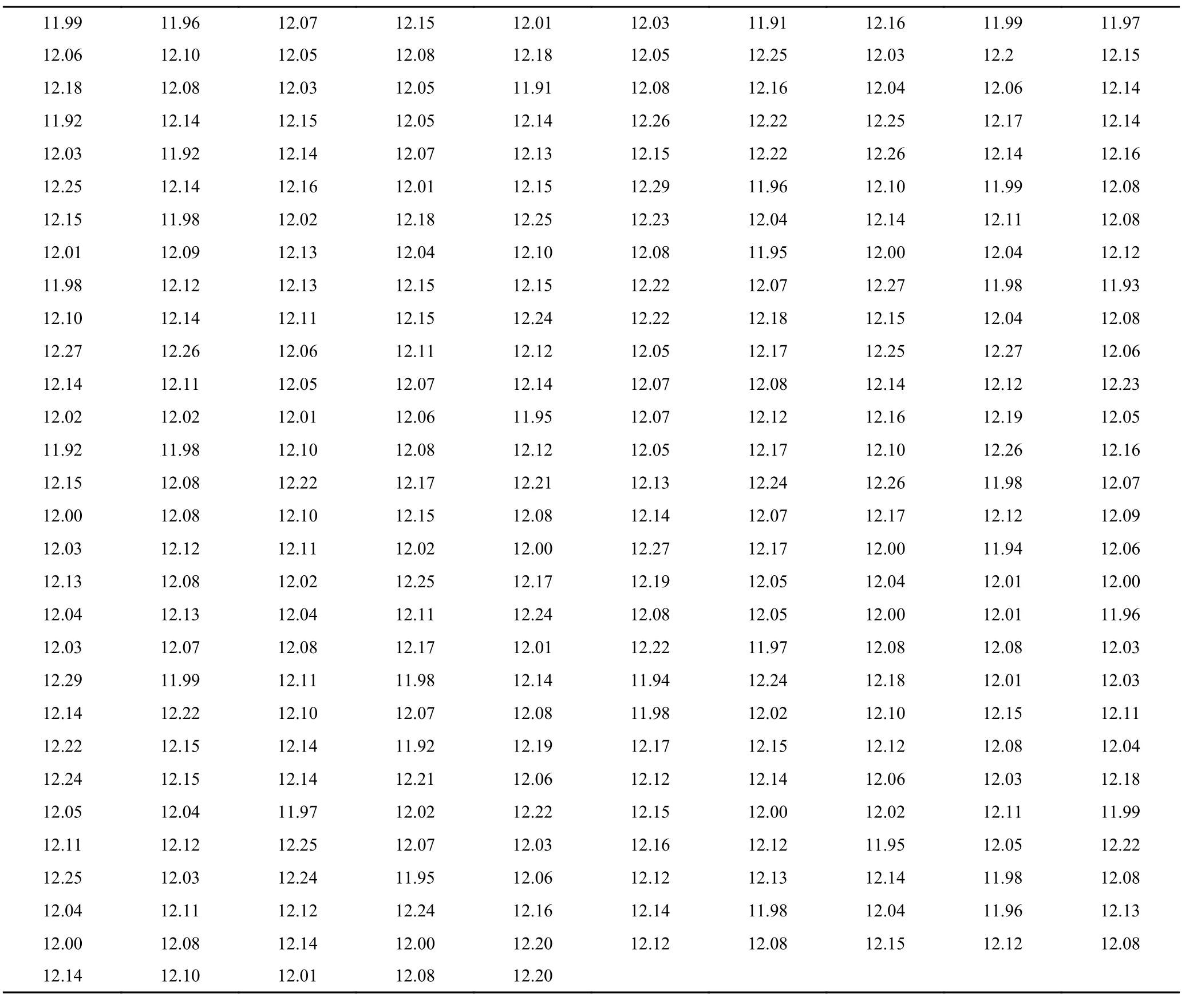
表5 295个数据Table 5 The 295 data

5 结论

CSP-T和Spk集成过程控制方案能够同时满足质量、成本和两类风险共四类约束。在长期平均检验数极限和平均检出质量极限约束下，建立了唯一可行的CSP-T方案，即极限过程下的CSP-T等值面方案。该最优CSP-T方案的第一类风险和第二类风险都很高。为同时将两类风险控制在给定风险水平，建立了基于Spk估计精确分布的风险控制方案。该风险控制方案以质量约束和成本约束对应的过程状态为控制点，以质量约束对应的过程状态控制第一类风险，以成本约束对应的过程状态控制第二类风险，构建质量和成本约束下同时满足两类风险的风险控制方案。

集成控制方案优势互补地发挥了CSP-T和Spk的作用。以基于Spk的风险控制方案改善了CSP-T两类风险都较高的现状。CSP-T的质量改善功能确保了无论过程质量如何波动，都能够得到合格的过程质量。

集成控制方案依据数据的计数特征驱动CSPT运行，依据数据的计量特征驱动风险控制方案运行，相比于传统控制方案，没有增加检验工作量。

图6 295个数据的正态概率图Figure 6 The normal probability plot of the 295 data

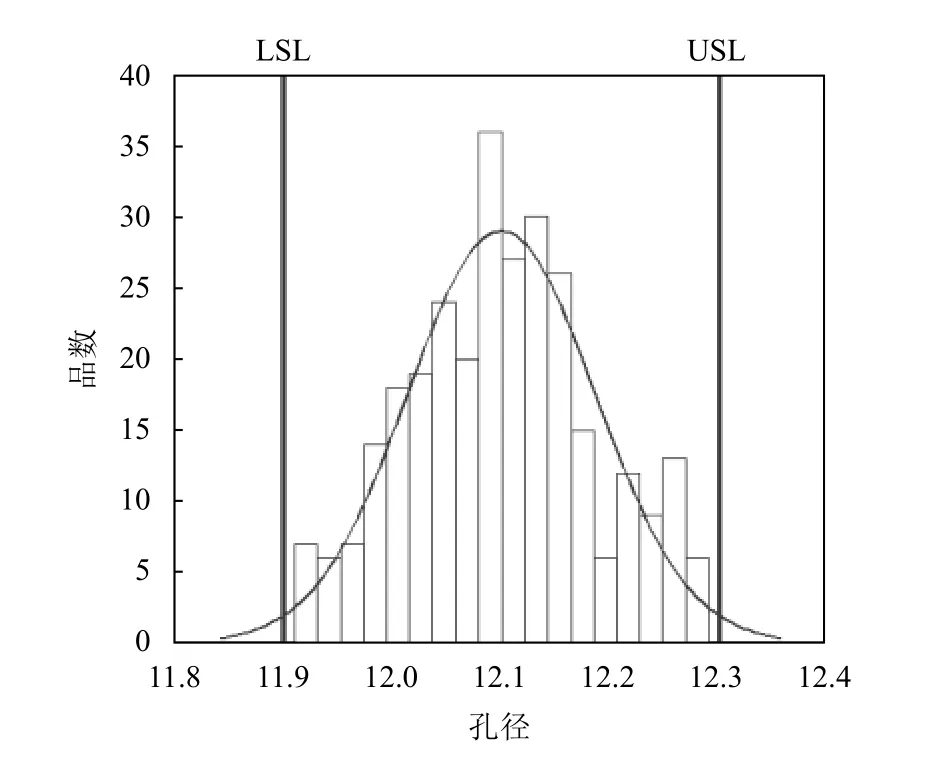
图7 295个数据的正态分布柱状拟合图Figure 7 The histogram of the 295 data

表6 集成控制方案与CSP-T方案的性能指标AFI 、A OQ和对比L(p)Table 6 Comparison on the performance indices A FI, A OQ and L(p) between CSP-T and the integrating control scheme

[1]柴天佑. 工业过程控制系统研究现状与发展方向[J]. 中国科学: 信息科学, 2016, 46(8): 1003-1015.CHAI Tianyou. Industrial process control systems: research status and development direction[J]. SCIENTIA SINICA Informationis, 2016, 46(8): 1003-1015.