基于LOF算法的多维混合型数据控制图设计

2020-07-22张乔微李艳婷

工业工程 2020年3期

张乔微，李艳婷

(上海交通大学机械与动力工程学院，上海 200240)

多元统计过程控制是制造业中必不可少的环节，针对多维正态数值型数据的控制图发展已十分成熟，最受欢迎的是HotellingT2控制图[1]、多元累积和(MCUSUM)控制图[2]和多元指数加权移动平均(MEWMA)控制图[3]。然而，这三类控制图都存在一定的应用局限性，它们都无法处理非正态型的数据。非参数控制图的出现为这一问题提供了解决方案。Bakir[4]通过设计秩统计量，打破了原有控制图在变量分布上的限制。Graham等[5]建立了一种非参数的EWMA控制图，并且证明了其在受控过程中的鲁棒性。除此之外，Zou等[6]通过一种自启动算法也实现了对非正态变量的有效监测。

然而，在实际应用中，需要考察的数据可能不仅仅只有数值型变量，往往还包括名义型和顺序型变量。例如在信用卡业务中，银行需要根据顾客的个人信息评估其申请资格。当待评估的顾客数量很多时，该过程可以被视为一个统计过程监测问题。其中，有资格的顾客可以被视为受控状态，无资格的顾客被视为失控状态。顾客的信息通常包括很多变量，其中有数值型变量，如顾客的年龄和银行卡余额。还有名义型变量，例如信用卡申请历史和申请目的。还有一些带有明显等级特征的顺序型变量，如学历等。在这种多维混合型数据的情况下，传统的数值型控制图已不再适用。如何有效地利用名义型和顺序型变量，是混合型数据控制图中的重点和难点。

Ning等[7]提出了一种可以有效处理混合型数据的Density-based控制图，该控制图将类别型变量转化成数值型变量，然后结合LOF (local outlier factor)算法[8]来考量数据的异常程度。该控制图使用自定义的数值来代替顺序性变量，将混合型数据转化为纯数值型数据，最后利用纯数值型控制图进行监测。然而随着数据复杂性和维度的提高，这类自定义数值转化的方法明显存在设计上的主观性和不合理性。Tuerhong等[9]使用高氏距离来衡量混合数据之间的距离，基于与其他数据的距离来衡量数据的异常程度，提出了基于高氏距离的混合型数据控制图。但是仅仅使用数据间的距离来衡量数据的集中程度是不准确的。Ding等[10]采用等级排名数来代替顺序型数据，并结合MEWMA控制图进行数据监测。其控制图的关键思想是顺序型变量的属性级别可以通过潜在的连续变量确定，混合型数据可以转换为一系列标准化的等级数。但是，这种控制图在实际场景中应用时有许多限制。首先，它无法处理没有任何数值特征的名义型变量。其次，用标准化的等级来替换数值变量会损失原数据信息，影响控制图的准确度。

现有的多维混合型数据控制图存在一定的设计缺陷和应用局限性，本文将介绍一种新的基于LOF算法的混合型数据控制图，简称MLOF (mixed-type data local outlier outlier factor control chart)控制图。该控制图的创新主要在2个方面。首先是采用了一种新的混合型数据距离量度方案。该距离量度方案针对数值型、名义型和顺序型这三类不同的变量分别制定了对应的量度规则，使用信息熵这一新思路来衡量名义型变量间的距离，合理解决了名义型变量的量化问题。另一创新在于利用LOF算法来衡量数据的异常程度，并且通过与新距离量度的结合，将LOF算法的应用范围从一维延伸到多维，从只能处理数值型数据拓展到可以处理任意类型的数据。本文通过仿真案例和实例，比较了MLOF控制图和现有多维混合型数据控制图的表现，证明了该控制图在混合型数据监测过程中的优势。

1 混合型数据距离量度方案

1.1 混合型数据距离量度综述

混合型数据距离度量的概念首先由Huang[11]在k-prototypes算法中提出。他将混合型数据间的距离转化为数值部分和类别部分之和。其中，数值部分是所有数值变量的算术平方和，类别部分是所有类别型变量统计量为0或1的总和。0代表2个类别型变量属性值相同，1代表2个类别型变量属性值不相同。除此之外，为了提高信息的利用率和计算的准确性，类别型变量还被赋予了一定的权重，权重值的大小取决于数值属性的分布。但是，该算法并没有提供具体的权重值确定规则。Ahmad等[12]认为越重要的属性越独立，与其他属性的共现性越小。他们基于属性之间的共现型定义不同属性值之间的距离。这种方法具有一定的逻辑合理性，但是随着属性和属性值数量的增加，由于属性配对引起的计算复杂度是不言而喻的。Cheung等[13]从信息熵的角度来定义属性的权重值。他们将不均匀度越大的属性赋予越高的权重值。但是，该方法仅适用于类别型变量，难以确定数值型变量的权重值。而且该方法将所有类别型变量合并为一个大类，削弱了类别型变量的重要度，这在类别变量多时显然是不合理的。统计过程控制中混合型数据的距离测量成为亟待解决的问题。本文介绍一个新的混合型数据距离度量方案，将混合型数据的变量分为数值型、名义型和顺序型3种类型，然后分别介绍每一种变量对应的距离度量规则。

1.2 数值型变量距离量度规则

数值型数据的距离可以直接由归一化后的欧氏距离来表示。一般地，数据Xi和Xj包含r个数值型变量，那么Xi和Xj数值型部分的距离可以表示为

特别地，如果数值型变量之间存在协相关矩阵S，那么使用马氏距离代替欧氏距离，数值型的部分的距离表示为

1.3 名义型变量距离量度规则

名义型变量往往只用来描述对象的某些特征，量化其不同属性值之间的距离并不容易。例如，颜色这一变量通常用来描述产品的外观，它的属性值包含红色、蓝色、绿色等等。这些属性值之间没有顺序性和数值性，无法用传统的数值方法来评估不同颜色之间的差异。如果简单地将不同属性值之间的距离设置为1，相同属性值之间的距离设置为0，无疑会造成信息量的丢失，影响结果的准确性。

本文在Cheung等[13]的研究基础上，使用信息熵的概念来定义名义型变量的距离量度，并使用不均匀性来表征信息熵的大小。新距离量度的创新点在于将信息熵最高的名义型变量的不同属性值距离定义为1，而其他名义型变量的不同属性值距离量度为其信息熵与最高信息熵的比率。通过这种处理方式，把每个名义型变量的距离量度值都限制在了区间 (0,1]中，同时可以在计算总距离时突出较高信息熵名义型变量的贡献值。例如在信用卡申请资格评估这一过程中，用户名这一变量的属性值很多，其不均匀性很低，其在新方案下得到的距离量度会很低。从逻辑上来说，这一项变量对评估结果的影响确实不大，不应该作为数据差异性衡量的重点考虑因素，这也验证了新方案的合理性。

具体的名义型变量距离计算方法可以归纳如下。首先，将名义型变量的信息熵SA用不均匀度表示，具体计算方法为

其中，mA表示名义型变量A中所有属性值的个数；F(Ai)表示属性值Ai所占的比例，i∈(1,2,···mA,)；max(S)表示所有变量不均匀度中最大的值。变量A不同属性值之间的距离dA可以表示为其信息熵与最大不信息熵的比例。

一般地，数据Xi和Xj包含m个名义型变量，那么Xi和Xj名义型部分的距离可以表示为

其中，当Xi和Xj在变量p上的属性值相同时，为零；属性值不相同时，由变量p的距离量度dp来表示。

1.4 顺序型变量距离量度规则

除了名义型变量之外，还有另一种类别型变量，即顺序型变量。这类变量的属性值虽然没有数值性，但是有着明显的程度上的差异，例如习惯使用大、中、小来描述一个产品的大小。从直观上看，属性值大和小的差异明显要大于属性值大和中之间的差异。为了利用顺序型数据的等级特点，和Ding等[10]处理顺序型变量的方法相似，同样利用等级数来代替顺序型变量的属性值，以量化不同属性值之间的距离。

对于一个顺序型变量，假设其一共有N个数据，在等级k上有nk个数据，那么这nk个数据对应的等级数为那么等级k对应的等级数可以表示为

一般地，数据Xi和Xj包含q个顺序型变量，那么Xi和Xj顺序型部分的距离可以表示为两者在该类变量上不同属性值对应的等级数差的绝对值总和

1.5 混合型数据距离量度方案

通过上述规则，将数值型、名义型和顺序型这3种变量的距离量度值都统一在[0, 1]区间内，那么2个混合型数据之间的距离可以被表示为其对应每一个变量的距离和。一般地，对于1个数值集D=每个对象都包括r个数值型变量、m个名义型变量和q个顺序型变量，那么数据Xi和Xj之间的距离D(Xi,Xj)等于这3类变量的距离之和，即

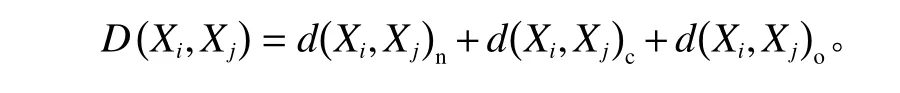
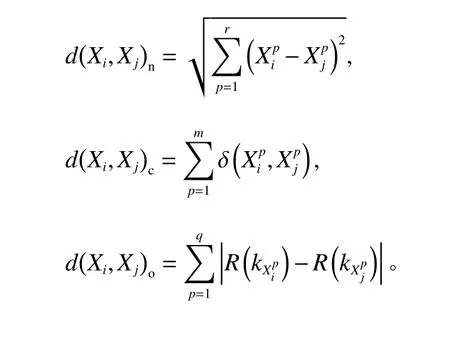
2 MLOF控制图设计

确定了混合型数据的距离量度方案后，采用LOF算法来衡量数据的异常程度，进一步完成MLOF控制图的设计。本节将详细介绍该算法的基本概念以及MLOF控制图的具体构建过程。

2.1 LOF算法

LOF算法是一种无监督的离群检测方法，是一种经典的基于密度的异常点监测算法，被广泛应用于故障检验[14]和多阶段过程监测[15]中。该算法基于数据的邻域信息和密度来确定数据的异常程度。它会给数据集中的每一个点计算对应的离群因子LOF值，若该值接近1，则其异常程度小。若该值越大，则该点的异常程度越高。LOF算法中的4个基本定义为k距离(kdistance)、可达距离(reachability distance)、局部可达密度(local reachability density)和局部异常因子(local outlier factor)。假设数据集D中有2个点a和b，上述4个概念的具体计算方法如下。

点a的k距离(k为整数)表示从点a到其第k个最近邻域点的距离，a的k个邻域点被记为Nk−distance(a)。b到点a的可达距离定义为

这表示如果b∈Nk−distance(a)，那么点b到点a的可达距离等于a的k距离；如果b∉Nk−distance(a)，那么点b到点a的可达距离等于点a、b之间的真实距离。

点a的局部可达密度定义为

lrdk(a)表示点a相对于其Nk−distance(a)中所有点的平均可达距离，反映了点a的局部可达密度。

点a的局部异常因子定义为

LOF算法根据点的局部异常因子值判断点的异常程度。如果该值越接近1，说明a与其邻域点密度差不多，a可能和邻域同属一簇；如果这个值小于1，说明a的密度高于其邻域点密度，a为密集点；如果这个比值越大于1，说明a的密度小于其邻域点密度，a越可能是异常点。

2.2 控制界限的确定

确定了监测过程统计量LOF，下一步就是确定控制图的控制界限。由于LOF的分布未知且难以构建，且实际检测过程中的数据量难以保证，采用Bootstrap[16]的方法来确定控制界限。重采样的过程如下。

1) 分别计算N个受控数据的LOF值：LOF1,LOF2,···,LOFN。

2) 通过Bootstrap方法从N个统计量中构建500～1 000个样本。

3) 根据设置的第一类错误值α 得到样本的100(1−α)th分位数。

4) 重复上述步骤，MLOF控制图的控制界限即为100(1−α)th分位数的平均值。

2.3 MLOF控制图

确定了控制图的监测统计量和控制界限，就可以通过计算新观测点的统计量来判断系统是否发生异常。一般地，对于一个已知的受控混合型数据集D={X1,X2,···,Xi,···,Xn}，将其划分为训练集和测试集2个部分。对于一个新的观测点Xn+1，MLOF控制图的构建和监测过程如下。

1) 根据新的混合型数据距离量度方案，计算测试集数据与训练集数据之间的距离，计算测试集所有数据的LOF值。

2) 使用Bootstrap重采样的方法确定MLOF控制图的控制界限H。

3) 计算Xn+1相对于训练集的LOF值L OFXn+1。

4) 如果 LOFXn+1≥H，那么代表监测系统失控，发出报警信号；如果 LOFXn+1＜H，代表没有监测到异常点，继续步骤3)。

3 案例分析

基于高氏距离的混合型数据控制图[9]是目前监测效果较好的混合型数据控制图。为了验证MLOF控制图的有效性，本文使用文献[9]中所采用的代表性数据集以及所提及的模型的监测结果来进行实验对比。

3.1 仿真案例

信用卡申请数据集[17]中包含653个有效对象和9个名义型属性。其中，357个对象属于类别1，296个对象属于类别2。本文将类别1看作受控状态，将类别2视为失控状态。在构建控制图的过程中，选取类别1中200个数据作为控制图的训练集，剩余的157个数据作为测试集。在原数据的9个名义型属性的基础上，增加了10个服从正态分布(均值为0，方差为1)的数值型变量，将案例扩充成了一个19维的混合型数据。研究在名义型变量数量发生变化或数值型变量发生不同程度均值漂移时，MLOF控制图和其他混合型数据控制图的监测效果。表1表示在不同仿真条件下，基于欧氏距离的局部K2控制图(Euclidean-basedK2)[18]、基于欧氏距离的全局控制图(Euclidean-based global)[19]、基于高氏距离的局部控制图(local gower)、基于高氏距离的全局控制图(global Gower)、基于高氏距离的控制图(Gowerbased和MLOF控制图(邻域个数k=20)在10次实验下的异常点检测率和标准差(第一类错误设置为0.05)。其中，a、b、c分别表示均值偏移量为0.5 δ、1 δ、2 δ。S1—S10、M1—M10、L1—L10表示名义型变量个数为0～9。对于一个控制图而言，检测率越高，标准差越低，其监测效果越好。加粗部分代表在该次仿真条件下表现最好的控制图检测率。

从表1可以看出，在大多数情况下，MLOF控制图的表现都是最好的。当名义型变量数量较多时，它优于基于欧氏距离的控制图。同时，在数值型变量均值偏移程度较大时，MLOF控制图比基于高氏距离的控制图监测精度更高，标准差更低。这些结果表明，相比起现有混合型数据控制图，MLOF控制图的检测率在类别型变量多、数值型变量均值偏移较大时具有更好的准确性和稳定性。

3.2 实例

德国信用卡数据集中[17]包含1 000个数据和20维属性，其中700个数据属于高信用度顾客数据，可以被视为受控数据。其余300个数据属于低信用度顾客数据，即失控数据。相比于信用卡申请数据集，德国信用卡数据中的变量描述更为具体。可以进一步将20维属性分为7个数值型属性、9个名义型属性和4个顺序型属性。每一类属性的具体信息如下。

数值型属性包括：持卡时间，储蓄账户余额，分期付款率，可支配收入百分比，居住年数，年龄，本银行现有信用卡数量，担保人数。

名义型属性包括：信用还款历史，申请目的，婚姻状态和性别，担保情况，财产情况，其他分期计划，住房情况，是否有手机，是否是外国工作者。其中，每一个变量的具体属性值及分布如图1所示。

根据本文的名义型变量距离度量规则，每个属性不同值之间的距离量度值计算结果如图2所示。从图2可以发现，属性值类型少或分布均匀的属性(例如变量“财产情况”，“是否有手机”)，具有更高的距离度量值，将对监测结果的影响也较大。这些规律与上文的逻辑一致，即不均匀度较高的属性应具有较大的信息熵，在统计监测过程中应予以更多权重。MLOF控制图距离量度的合理性被进一步验证。

顺序型属性包括：账户状态、储蓄状态、工作年限和工作类型。根据顺序型变量距离量度规则，可以把顺序型变量的属性值转化为相应的等级数。具体的转化结果如表2所示。

确定各类属性的距离量度规则后，将前500个高信用度顾客数据作为训练集，其余200个高信用度顾客数据集作为测试集，结合LOF算法和Bootstrap方法完成MLOF控制图的构建。通过计算ROC曲线[20]下的面积，即AUC值，与基于高氏距离的控制图进行监测效果比较。AUC值越大，表示控制图的监测效果越好。图3展示了在设置不同邻域个数k(2～50)的的情况下，MLOF控制图的AUC值。从图中可以看出MLOF控制图的监测效果并没有随着k的变化有明显规律性的变化，在德国信用卡数据集下，当算法的邻域个数为4时，MLOF控制图的监测效果最佳。

表1 信用卡申请数据集下不同控制图的检测率1)Table 1 Detection rates (%) of different control charts on credit approval dataset %

表3列出了MLOF控制图和其他控制图的最佳AUC值。从表中可以看出，MLOF控制图与局部高氏距离控制图表现相似，都比全局高氏距离控制图和高氏距离TG2控制图要好。为了进一步比较这2个控制图，表4列出了在不同邻域个数k下MLOF控制图与局部高氏距离控制图的AUC值。从表4可以看出，当邻域个数k大于10时，MLOF控制图优于局部高氏距离控制图；而当k较小时，则相反。这个现象可以从2种控制图的原理来解释。MLOF是一种基于密度的方法，相比于局部高氏距离控制图，当邻域个数较多时可以较准确地反映出更多的聚类特征。然而，局部高氏距离控制图是一种基于距离的方法，较大的k会影响监测的准确性。这表明MLOF控制图可能更适用于数据量大，聚类情况复杂的监测场景中。

图1 德国信用卡数据集名义型变量属性值分布结构图Figure 1 The structure of ordinal categorical variables for German credit dataset

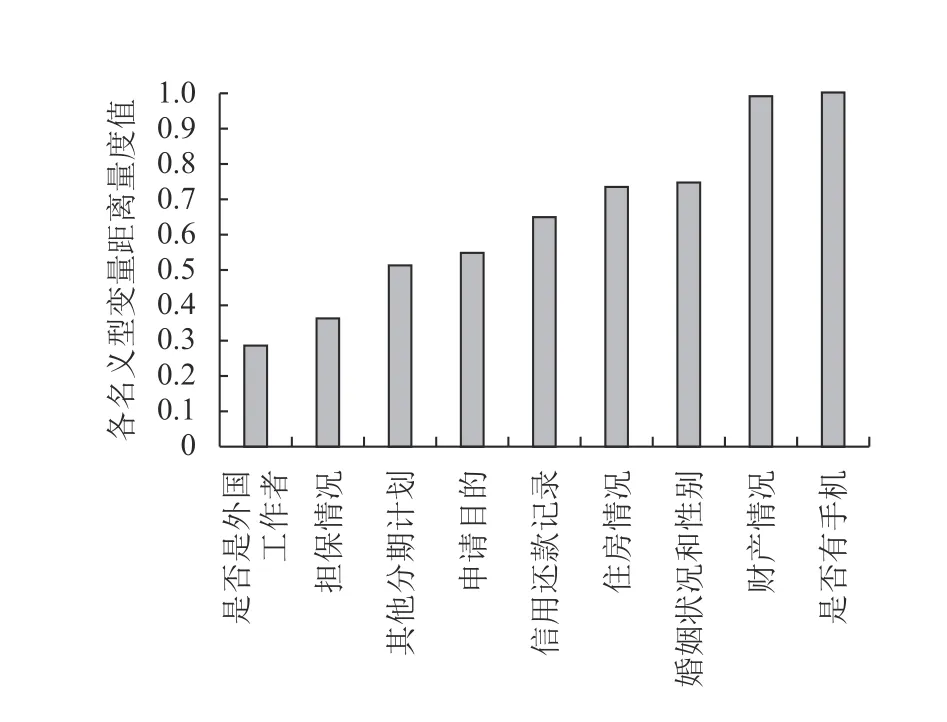
图2 德国信用卡数据集名义型变量距离量度值Figure 2 The distance measures of ordinal categorical variables for German credit dataset

4 结论

混合型数据监测问题是多维数据过程控制中的重点和难点。本文打破了传统距离量度方案对变量类型的限制，充分利用名义型数据的信息熵和顺序型数据的等级特性，建立了新的混合型数据属性距离量度方案。通过将LOF算法与新的距离度量结合，打破了传统的LOF算法的应用局限性，完成了新MLOF控制图的设计。仿真和实际的案例都证明了新控制图的良好表现，这意味着它将在基于多维混合型数据的统计过程控制和聚类分析中都具有很好的应用前景。在未来，还有以下2个方面值得研究：1) 是考虑结合降维方法对数据进行预处理，增加距离量度的准确性：2) 合理制定时间、空间这类属性标签的量化规则，使MLOF控制图的应用范围可以拓展到含时空性的更复杂的场景中。