考虑乘客不完全理性行为的轨道交通车站应急疏散方法研究

毛亚兰，张 锦

(西南交通大学 交通运输与物流学院，四川 成都 610031)

随着城镇化进程的推进，居民生活水平日益提高，出行需求快速增长，城市轨道交通以其大运量、安全、快速、准时等优点成为居民出行的首要选择之一。据 《城市轨道交通2 018年度统计和分析报告》 数据，截至2 018年末，中国大陆地区已有35个城市开通城市轨道交通，运营线路185条，车站3 394座，运营线路总长度达5 761.4 km。城市轨道交通车站多具有半封闭、结构复杂、客流量大等特点，在突发事件下，乘客由于恐慌无措，想要尽快到达出口等心理，容易产生推搡、逆行等过激行为，给疏散工作造成阻碍，甚至造成重大的人员伤亡和财产损失。因此，突发事件下，城市轨道交通车站客流安全疏散问题的研究具有重要意义。

掌握车站内各路径的疏散客流分布情况，是合理制定应急疏散方案，引导乘客安全、高效疏散的前提。目前国内外针对轨道交通疏散客流分配的研究，主要借鉴道路客流分配的基本理论和思想，以Wardrop[1]的用户均衡原理(user equilibrium，UE)为基础建立模型。唐涵[2]结合Wardrop均衡理论，建立了地铁车站疏散路径配流模型。刘杨等[3]提出了基于用户均衡理论的疏散人员出口分配方法。但用户均衡理论假设乘客在进行路径选择时完全理性，而由于经济、文化、健康等个体生理心理差异的存在，个体的实际决策行为是有限理性的。1 972年，英国学者Wood调查了952起火灾中2193名人员的行为。随后Bryan[4]也在美国开展类似调查，并与Wood的调查结果进行比较，首次验证了文化背景对人员疏散行为的影响。Heliövaara等[5]提出实际情况下，疏散过程中不同行人获得的决策信息具有一定局限性，其决定并不是客观理性的。因此，基于用户均衡理论的相关疏散模型及方法存在一定不足，有学者开始将前景理论(prospect theory，PT)应用到应急疏散行为的研究中。Liu等[6]考虑突发事件下个体的应急反应，提出了基于累积前景理论的风险决策方法。Ren等[7]结合前景理论和模糊决策理论，建立了模糊前景决策矩阵，并引入能量和熵描述决策值，提出了基于前景理论的模糊热力应急决策方法。Zhang等[8]考虑个体的心理行为及不同应急疏散情形，提出了基于前景理论的应急疏散方法。Ding等[9]提出了突发事件下基于前景理论的多准则优化解决方案。陈小君等[10]基于前景理论和时空经济分析框架，提出了描述交通基础设施应急疏散管理过程中群体决策行为的概念模型，认为可以通过实时信息供给降低非理性行为的发生概率。任其亮等[11]分析出行者的决策行为，以疏散预测时间为参照点，建立了应急交通疏散路径选择模型。卢勇利等[12]引入累积前景理论和集对分析，提出了考虑决策者风险态度的多准则决策方法。

综上，目前研究中关于城市轨道交通车站的应急疏散研究多基于乘客完全理性建立疏散客流分配模型，与个体的实际疏散行为存在较大差异。考虑个体的不完全理性行为，已有学者将前景理论应用到大型建筑、道路交通等场所的应急疏散决策行为研究中，但轨道交通车站的疏散客流分配方面还未涉及。因此本文提出基于前景理论的应急疏散客流分配方法，为轨道交通车站安全疏散设施设计以及突发事件下的应急疏散方案制定提供依据。

1 基于前景理论的客流分配方法

1.1 前景理论概述

前景理论由Tversky等[13]提出，认为个体的风险决策可以分为编辑和估值2个阶段。在编辑阶段，个体凭借“框架”、参考点等采集和处理信息；在评价阶段，个体依赖价值函数和主观概率的权重函数对信息予以判断。通常个体在进行决策时，会根据先验信息确定一个参考点，再将决策的各项属性与参考点进行比较，若高于参考点则视为“收益”，否则视为“损失”，只有当决策的总体收益大于损失时，该决策才会被接受。在前景理论中，通常用价值函数v(x)和决策权重函数w(p)来描述个体的决策行为。价值函数是主观性质的函数，为当前值与参考点的差值，其中参考点由个体的主观判断确定。决策权重函数是主观概率函数，是个体对事件发生的风险概率p作出的主观判断，体现了个体的风险态度。价值函数和决策权重函数共同构成前景函数，影响个体的最终决策。前景函数的表达式[13]为

其中，Vi为选择肢的前景值，v+(x)为收益价值函数，w+(p)为收益权重函数，v−(x)为损失价值函数，w−(p)为损失权重函数。

收益价值函数v+(x)与 损失价值函数v−(x)的表达式为[14]

其中，x0为参考点，a为收益追求系数，b为损失规避系数，且0＜a＜b，说明决策者在面对损失时比面对收益时更加敏感。 α、β＞0，表示决策者的风险偏好水平，其值越大表明决策者对于风险越敏感。

前景理论认为，人们在决策时往往有高估低概率事件和低估高概率事件的倾向，而对中间概率的变化相对不敏感，决策权重函数的表达式为[14]

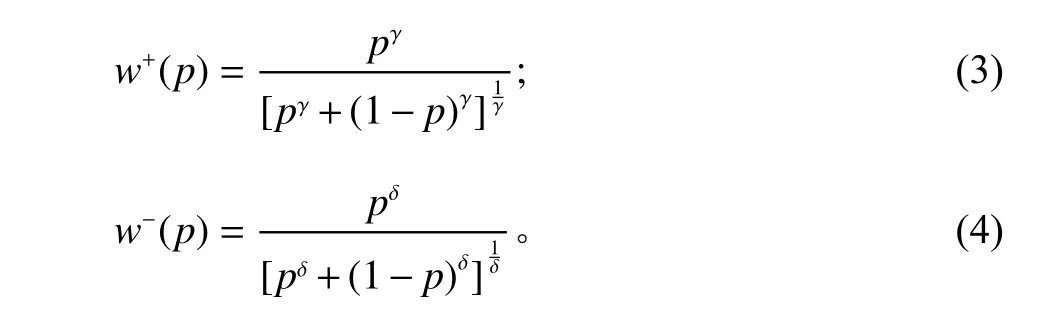
其中，γ为收益权重系数，δ为损失权重系数，0＜γ＜1，0 ＜δ＜1。

1.2 基于前景理论的疏散客流分配模型

利用图论的思想，可以将城市轨道交通车站内部结构网络化为一个有向图G=(N,E,O,D)，其中，N为疏散节点集合，包括站台、设施连接处、闸机和出站口等；E为走行设施构成的有向边的集合，这里指连接2个节点之间的走行设施，包括楼梯、自动扶梯、通道等，其边长为设施长度；O、D分别表示疏散起点集合和终点集合，这里的起点和终点分别指站台和出站口。根据国家标准[15]，安全疏散时间不大于360 s的路径为有效路径。车站内部的客流疏散应在有效疏散路径上进行。在疏散过程中，乘客在进行路径选择时主要受路径走行时间的影响，而路径走行时间主要包括区间走行时间和延误时间，则路径费用函数为

在交通环境下，路径费用小于参考点时表示收益，大于参考点时表示损失，因此设施rs间第k条路径的价值函数为

其中，C0为参考点。

决策者对参考点的选取与决策者对突发事件的主观感受有关。在同一突发事件下，由于先验信息不同，不同乘客对参考点的选取也不一样。本文分析了应急情况下乘客的心理状态，取在自由流下乘客的平均疏散时间为参考点。假设 εrs相互独立且服从Gumbel分布，则路径k的客观客流分配比例可以采用MNL(multinominal logit)模型

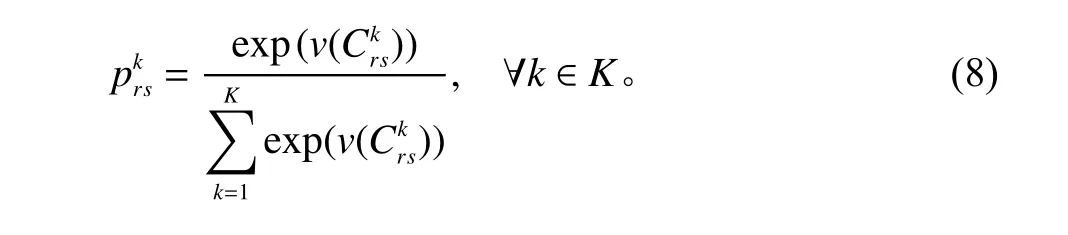
由于人们在决策时有高估低概率事件和低估高概率事件的倾向，则乘客选择路径k的主观概率为

路径k的实际客流分配比例为

本文参数取值采用Tversky等[14]的研究结果，如表1所示。

表1 参数取值Table 1 Parameter value

1.3 求解算法

利用图的深度优先遍历(depth first search，DFS)搜索算法搜索有效疏散路径，具体方法如下。

1)将车站内部结构网络初始化为有向图G=(N,令集合设v(ni)=0，i=1。其中，S为已遍历节点集合；T为未遍历节点集合；v(ni)为路径价值；K为有效路径集合；ϕ为空集。

2) 遍历节点ni的相邻边，若相邻边集合R=ϕ，则算法终止，否则转入下一步。

3) 若R≠ϕ，则计算边eij的疏散时间tij、当前路径疏散时间t(nj)=t(ni)+tij及其价值v(nj)=v(ni)+vi j，

4) 判断tij是否不超过360 s，是则转入下一步，否则删除nj，返回步骤2)。

5) 判断nj∈D是否成立，若是则得到有效路径Kk及其疏散时间Tk、路径价值vk，否则令nj=ni，同时设集合并返回2)。

结合连续平均法 (method of successive averages，MSA)，根据路径前景值将待疏散客流分配到有效路径上，具体如下。

1) 初始化，得到车站内部结构网络有向图G=(N,E,O,D)、OD对数以及待疏散人数Q。

2) 在自由流下，计算各区段的初始走行时间tij0及价值函数vij0，利用图的深度优先遍历(DFS)算法搜索有效路径，得到初始有效路径集合K及各路径疏散时间Tk、路径价值vk。

3) 计算路径k的客观客流分配比例

4) 计算乘客选择路径k的主观概率w(pk)及前景值Vk，得到路径k的实际客流分配比例得到初始解迭代次数n=0，路径价值前景值

5) 计算客流密度及分配客流后各区段的疏散时间，更新有效路径集合，不同客流密度下走行时间的计算参照文献[16]，令n=n+1，计算区段价值路径价值路径前景值

路径搜索算法、模型求解算法流程分别如图1和图2所示。

2 案例分析

2.1 案例简介

太升南路地铁站位于成都市太升南路和忠烈祠街的交汇处，市中心太升路商圈内，是成都地铁4号线一期站点。太升南路地铁站有B、C、D3个出口，站台与站厅中央由1部楼梯连接，两侧各有上行、下行2部自动扶梯连接。站厅与各个出口由通道连接，B口有2部楼梯，C口有1部楼梯及上下行2部自动扶梯。D口有1部上行自动扶梯及1部楼梯。根据调研结果，得到太升南路地铁站的内部疏散通道分布如图3所示，部分楼梯通道数据如表2所示。

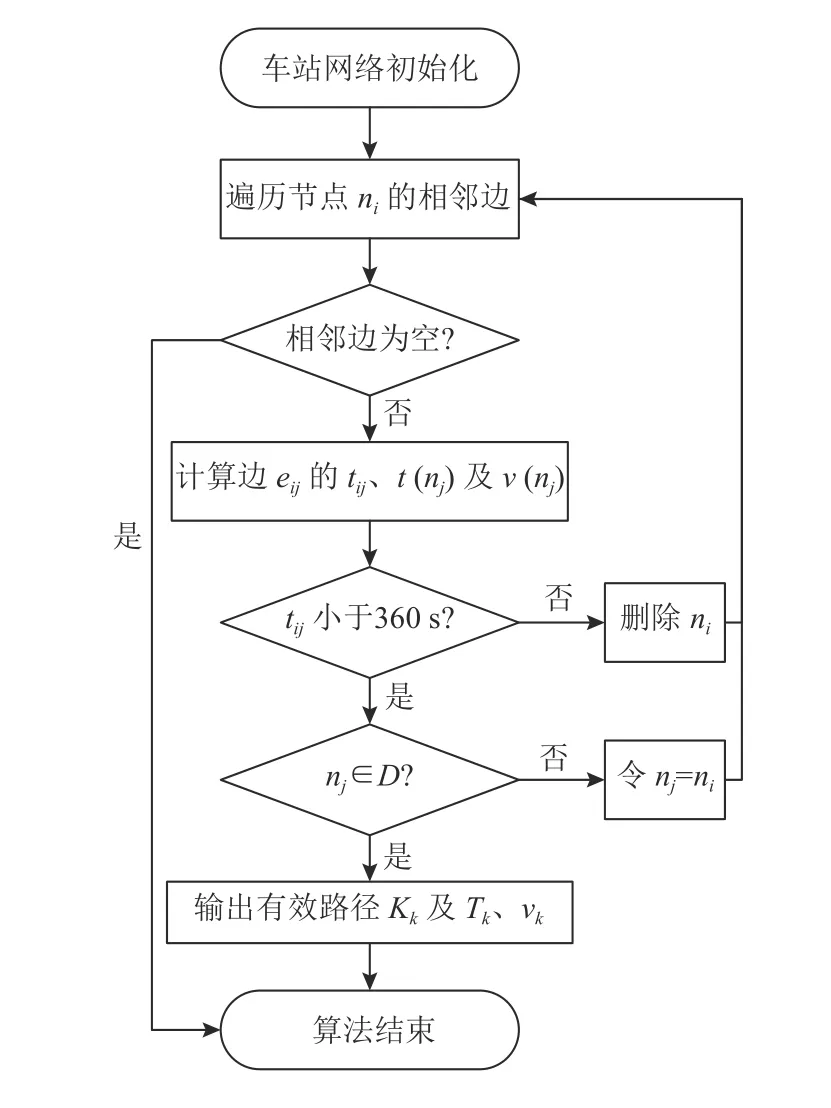
图1 DFS算法Figure 1 DFS algorithm

图2 MSA算法Figure 2 MSA algorithm

根据实地调研结果，将车站结构网络化，得到太升南路地铁站网络图如图4所示。其中，节点1为站台，节点2、3、4为楼梯/自动扶梯出口，节点5、6、9、10为闸机(假设应急状态下，闸机全部开放)，节点8、13为通道连接点，节点7、11、12为楼梯/自动扶梯入口，节点B、C、D为出站口。节点之间的数字表示疏散通道长度。

图3 太升南路地铁站疏散通道分布图Figure 3 Taisheng South Road subway station structure

表2 太升南路地铁站部分楼梯通道数据Table 2 Taisheng South road subway station partial staircase data

事故场景：4号线地铁驶入太升南路地铁站时，车厢起火，为了保证乘客安全，地铁到达太升南路站后，需将站内乘客全部疏散。

待疏散人员：4号线站台一列地铁载客量为750人，站台待疏散人员共50人，之后的地铁将不再停靠太升南路站。因此，总待疏散人数为800人。

2.2 疏散客流分配

利用DFS算法进行搜索，得到突发事件下太升南路地铁站的有效路径集合，如表3所示。

利用Matlab进行编程计算，得到基于前景理论的太升南路地铁站应急疏散客流分配结果如表4所示。

总疏散时间等于各路径疏散时间的最大值。因此，基于前景理论的客流分配方法，最终得到的总疏散时间为317.8 s。

2.3 仿真

图4 太升南路地铁站网络图Figure 4 Taisheng South road subway station network

目前常用的交通仿真软件主要有Legion、Steps、SimWalk和AnyLogic等，均主要用于行人流微观仿真，不同的仿真软件有不同的使用模型。为了便于建模，用社会力模型描述行人运动，这里选用AnyLogic进行突发事件下的车站应急疏散仿真。主要仿真过程包括构建站内仿真环境，创建行为流程图，运行仿真以及结果分析评价。构建仿真环境可以通过利用图像编辑器绘制或导入车站布局图，本文通过绘制得到太升南路地铁站的仿真布局图，所使用比例尺为1 m=10像素。绘制完成后，用将不同走行速度的区域隔开，用 将乘客不能到达的区域隔开，用 将站台绘制为目标起点，各出站口作为目标终点。为行人个体，个体仿真的粒子直径为0.4～0.5 m。参考文献[15]，设置个体初始速度为0.6～0.8 m/s，水平疏散速度为1.0～1.2 m/s，楼梯/自动扶梯疏散速度为0.7～1.0 m/s(假设发生火灾时所有自动扶梯停运)。按照2.1中设置的事故场景，以及2.2节中基于前景理论的客流分配结果进行仿真，得到疏散后期的车站客流密度图，如图5所示。图中不同颜色表示不同的客流密度状态，蓝色表示畅通，红色表示拥堵，具体如图左侧标尺所示。按照同样的方式，利用基于乘客完全理性的均衡客流分配方法对待疏散乘客进行分配，并按照分配结果进行仿真，得到车站疏散客流密度图，如图6所示。疏散用时对比如表5所示。

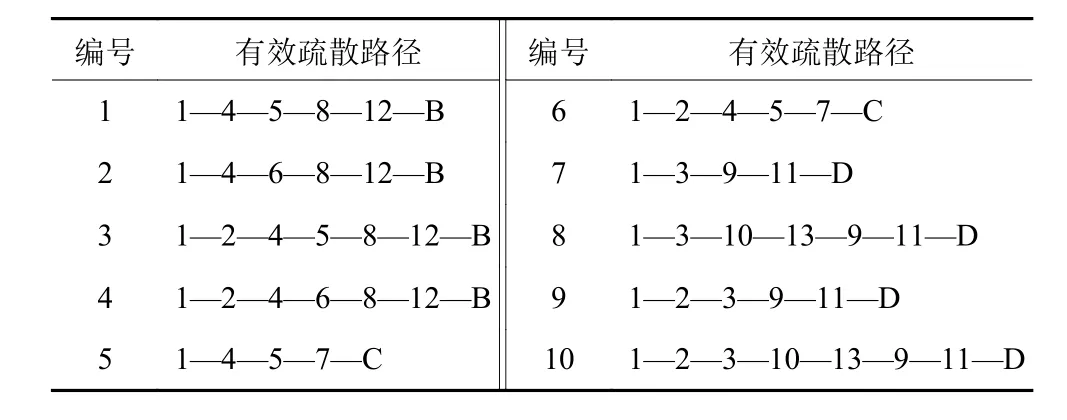
表3 有效路径集合Table 3 Effective path set

表4 前景客流分配结果Table 4 Prospector passenger flow assignment result

图5 前景分配疏散客流密度图Figure 5 Evacuation passenger flow density map based on PT

图6 均衡分配疏散客流密度图Figure 6 Evacuation passenger flow density map based on UE

1) 疏散结果对比。从图5和图6可以看出，基于前景理论的客流分配方法得到的配流结果更符合实际生活中乘客在突发事件下的决策行为，即慌乱无措，对整个路网流量没有正确的判断，盲目从众，造成拥堵，导致疏散效率降低，疏散时间更长。而基于用户均衡理论的客流分配方法，建立在乘客完全理性的假设上，得到的配流结果明显不符合常识。

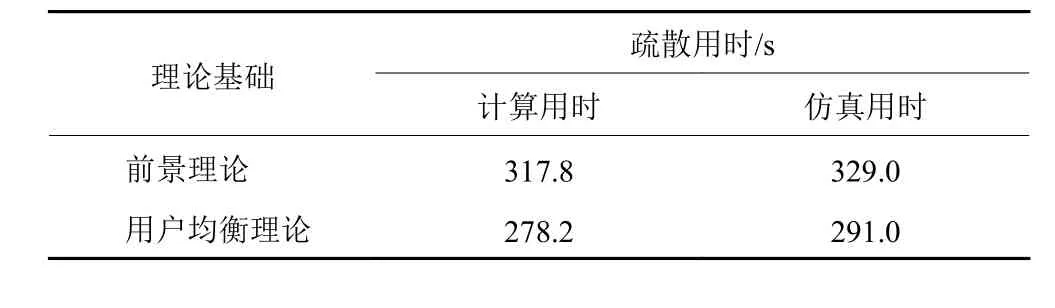
表5 疏散用时对比Table 5 Evacuation time comparison

2) 疏散用时对比。基于前景理论的客流分配方法得到的总疏散用时高于用户均衡配流方法得到的总的疏散用时。这是因为用户均衡的配流方法假设乘客处于完全理性状态，认为所有乘客都会按照客流分配结果进行路径选择。而前景理论考虑乘客的非理性行为，根据相对收益/损失时间来进行路径决策，更加符合乘客的实际决策行为。仿真用时略高于计算用时，是因为计算时依据的速度−客流密度拟合公式与乘客实际运动规律存在一定误差，而仿真中乘客的速度设置为一定范围。

3) 拥堵点分析。从图5可以看出，在疏散过程中，客流分流、交叉、聚集处明显拥堵。由于乘客的急于出站、不愿绕路等心理，导致通道e39和通道e45的客流密度在短时间内快速增加，而通道e1 013和通道e68均只有少量乘客通过，D出站口较B、C出站口明显拥堵，而B口较C口更堵。如图7所示，主要的拥堵点为站台—站厅各楼梯/自动扶梯出口处(节点3、节点4)、通道分流处(节点3、节点4、节点5)、通道合流处(节点8、节点9)、扶梯/自动扶梯入口处(节点11、节点12)。

图7 拥堵节点示意图Figure 7 Congested node schematic

3 结语

本文考虑突发事件下乘客的不完全理性行为，以前景理论为基础，提出了城市轨道交通车站疏散客流分配方法，并以成都太升南路地铁站为例，完成火灾情景下的基于前景理论和基于用户均衡理论的疏散客流分配及仿真对比分析。仿真结果表明，基于前景理论的客流分配方法得到的配流结果，比用户均衡配流方法得到的配流结果更符合实际应急疏散结果；在疏散过程中，客流分流、交叉、合流处为主要拥堵点，在安全疏散设施设计、应急疏散方案制定时，应优先予以考虑。进一步的研究工作是复杂环境下动态的疏散客流分配，研究拥堵点确定后疏散引导策略的制定。