基于突发事件的城市地铁客流应急疏散模型与仿真分析

熊国强，雷嘉烨

(西安理工大学 经济与管理学院，陕西 西安 710048)

随着城市人口不断的增长，城市交通拥堵已成为居民生活中迫切需要解决的问题之一，城市地铁交通的需求日益强烈。2 017年国务院发表的《中国交通运输发展》白皮书指出，“十三五”期间，我国将新增城市地铁运营里程约3 000 km。预计到2 023年，地铁交通运营里程将超过8 000 km，城轨车辆密度将达到7.4 辆/km。地铁因其快速便捷、安全性高等特点，成为了居民出行的首选交通工具。随着地铁网络的快速发展，大客流聚集和通道拥堵等问题日益严重，尤其在突发事件发生时，站内拥挤狭窄，很难在最短时间内将乘客疏散到安全区域，极易造成重大的人员伤亡和财产损失，进而产生不良的社会影响。因此，如何制定突发客流情况下有效的应急疏散方案是工业工程领域亟需研究的重要问题。

针对人群疏散问题，国内外均有一定研究。其中，Togawa[1]根据人群疏散时间的影响因素，建立了人群疏散时间最短的计算模型和建筑物内人员疏散的经验模型。Muramatsu等[2]提出了对元胞自动机模型进行假设之后的二维模型——格子气模型，提出行人靠右通行最优的交通规则。Song等[3]运用改进的元胞自动机模型量化疏散过程中行人间的3种相互作用力，发现疏散过程中起重要作用的主要是引力、斥力和摩擦力。Li等[4]提出了以总疏散时间最短、所有疏散人员行走路线最短和减少拥堵为目标的多目标疏散模型。Shiwakoti等[5]提出了客流紧急疏散中的可能行为，并对1 134名列车乘客进行了调查，运用有序logit模型模拟相关的调查数据，结果发现区别性别的疏散行为存在明显差异，年龄组之间差异不明显。Song等[6]模拟了相对较大客流密度的地铁列车火灾案例，并进行仿真研究，比较必须疏散时间和可用疏散时间，预测出安全疏散分布。

近年来，国内学者结合我国国情也开展一些相关工作。岳昊等[7]运用元胞自动机原理仿真研究了不同方向比例与不同系统规模的对向行人流的速度密度、流量密度之间的关系。何理等[8]设计了轨道交通突发事件下乘客疏散意识及疏散行为的调查问卷。任常兴等[9]对人流密集场所疏散能力的影响因素进行了分析，并给出了不同场景下不同特性行人的运动速度取值。张海均等[10]在传统社会力模型的基础上，增加避免碰撞机制，引入行人运动感知域，再现了行人流自组织现象。马培[11]以南方某地下车站为例，采用地铁规范设计理论计算出疏散时间，并基于连续模型的疏散软件Pathfinder进行仿真，结果表明行人从站台全部疏散的时间均小于6 min。刘志萍[12]基于AnyLogic软件对地铁内的突发情况进行客流仿真，并对疏散时间进行初始分析和优化分析，得出了缩短疏散时间的有效方法。

从现有文献看，大多数研究主要关注疏散能力影响因素的辨别和大客流疏散时间的探讨，鲜有考虑多因素影响下对疏散点和主要拥挤点进行地铁客流的应急疏散的研究。基于此，本文首先结合地铁突发客流的客流分布，建立行人最优路径选择模型和行人移动模型，然后基于元胞自动机理论，构建障碍物绕行模型和变道超越模型，最后以西安地铁三号线为例，通过AnyLogic仿真，对突发事件下地铁客流应急疏散的过程进行分析。

1 客流疏散组合模型构建

地铁应急疏散管理的本质是对行人的管控，所以在建立相关模型时应考虑与行人有关的影响因素。本文在调研分析的基础上主要考虑行人如何选择路径能最快撤离、行人疏散时的移动行为特征、疏散途中如何避开障碍物、如何超越和变道等4个主要影响因素。

人群疏散的仿真模型主要有社会力模型(social force model, SFM)、排队论模型以及元胞自动机(cellular automata, CA)和多智能体模型。但在复杂情况下，元胞自动机模型在允许高速模拟、优化撤离程序等方面明显优于其他3个模型。在元胞自动机模型中，行人由以网状形式随机移动的细胞表示，即通过离散步骤执行移动。基于此，本文将突发事件下大客流中的个体设置为一个单元节点(i,j)，车站划分成由相同节点组成的网格。其中，节点是网格的基本单位，并且在任一时刻，每一个节点网格或为空，或被障碍物和行人占用。

1.1 最优路径选择模型

在突发情况下，为快速移动到车站出入口，行人将选择最短直线路径逃生[13]。考虑到现实情况，模型引入了最短路径函数，并将行人在疏散移动过程中因周围环境的变化而不断选择局部最短路径的情况纳入考虑范围，以提高准确程度。结合以上因素，最终行人路径选择过程如图1示。其中，Cij为局部初始位置vi到局部目标位置vj的距离，n为目的地。

路径选择过程中局部最短路线Z的优化函数[14]为

式中，xij为选择路径(i,j)的状态变量，选择路径(i,j)时为1，不选择路径(i,j)时为0；E为路线的集合；k为选择某段路径时的起点。

根据0-1规划模型，起点为1，终点为n的情况下，从1出发的所有弧必然有一条在最短路上，即对于选择路径和从某点开始选择的路径需满足最短路径条件从某点选择路径到达目的 地时也必然有一条最短路径，即

1.2 行人移动模型

根据元胞自动机原理[15]，地铁站内行人移动模型将行人的移动分为8个方向格点移动，如图2所示。

图2 行人移动格点图Figure 2 Pedestrian moving lattice map

根据图2中行人的不同移动方向，分析地铁站内行人的移动速度V与客流密度K，客流量Q与客流密度K之间的关系[16]。

1) 移动速度V与客流密度K之间的关系。在正常情况下，行人移动速度不会随客流密度的增加而变化，但当发生突发事件或者突发大客流情况发生时，客流密度将不断增大，行人之间的空间将逐渐减小。此时行人与行人之间互相产生了影响，导致行人的速度产生变化，小于正常移动速度。在自由流状态下，行人的自由速度最高可达到Vm，对应的人群密度为Km；稳态流的状态下，行人的速度会上升到最大值Vc，客流密度达到最佳值Kc；超过最佳密度后，逐渐出现阻塞流状态，人群的速度会大幅度降低直至停止，如图3所示。

图3 行人的移动速度、客流量与客流密度的关系Figure 3 Relationship of parameters among movement speed,passenger flow, and traffic density

2) 客流量Q与客流密度K之间的关系。在自由流状态下，行人不受干扰时都可以保持自身的速度行走，此时客流量会随着客流密度的增加而增加；在稳态情况下，客流密度的增加会导致客流量的增加，此时并未出现拥堵；在阻塞的状态下，客流量都随密度的增加而减少。当地铁站点内的客流密度超过了最佳密度Kc值时(最佳密度Kc由车站的规模和行人流中的对向行走比例决定)，则会诱发大客流现象。由于客流密度增加所引起客流量的增长无法弥补速度降低对客流量的制约，此时客流量将会随着密度的增加而下降，即客流密度的增加，导致客流量呈现先增后减的趋势。如果客流密度再次增加至Kj，行人的速度和流量都将为0，如图3所示。

1.3 障碍物绕行模型

行人在疏散过程中可能会碰到障碍物，从现实来看，障碍物对客流疏散的影响并不会随着时间变化而改变。因此，仿真模型需要考虑行人自主绕开障碍物的相关行为特征。

如图4所示，选取一个障碍物，将其抽象设置为长是1个格点、高为2个格点的矩形(格点的大小需根据不同的障碍物设置)。行人当前所处位置为S0(x0,y0)，以方向绕开障碍物到达目标位置St(xt,yt)。为保证障碍物对行人不会产生影响，模型中对障碍物的外围设置一层安全区域，通过障碍物边界值b将障碍物的4个外围划分成A、B、C、D 4个范围。为简便表达行人移动方向，将用坐标形式呈现，例如(0, 1)，(1, 0)，(0, −1)等。

通过流程图法描述行人绕行障碍物的实现过程，如图5所示。

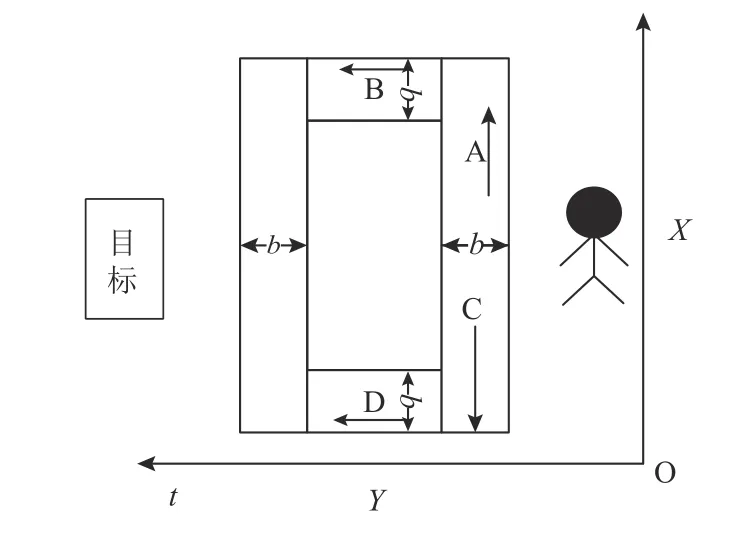
图4 障碍物绕行模型Figure 4 Obstacle avoidance model

图5 障碍物绕行流程图Figure 5 Flow chart of obstacle avoidance

1.4 变道和超越模型

因个体移动速度存在差异，地铁站内行人在疏散过程中会出现后面的行人需绕道穿越前面行人的情况[17]。变道和超越模型类似于障碍物绕行模型但具有差异。障碍物绕行模型是基于大范围的搜索，而被绕行的障碍物始终静止；变道和超越模型是基于小范围的局部搜索，而且模型中需要被绕行的行人处于移动状态。由1.2节可知行人周围划分为8个移动方向，假设行人甲当前所处位置为S0(x0,y0)，速度为v0；行人乙位于行人甲前面，速度小于行人甲，两者皆向目标位置疏散，如图6所示。

图6 行人变道和超越模型Figure 6 Lane change and transcendence model

在移动途中，行人甲和行人乙同方向移动，甲在移动过程中逐渐接近乙进而超越乙。已知人的最大视野范围为200°，而当行人甲需要变道时，可改变方向范围为至视线所在180°内[18]。因此，图6中行人甲可以转向为D1、D2、D3、D4、D8。行人甲变道与超越的实现过程如图7所示。其中d甲乙为甲乙行人间的距离，r甲+r乙为2个行人刚好接触时的距离。行人变道和超越流程图见图7。

2 客流疏散仿真模拟

AnyLogic是支持模拟方法的常用仿真工具，包括系统动力学、流程导向型(又叫离散事件)以及基于主体的建模模拟方法等[19]。本文利用AnyLogic中的行人库来仿真模拟地铁运营突发事件下的客流疏散过程，AnyLogic建模如图8所示。

据中国城市轨道交通协会发布的《城市轨道交通2 018年度统计和分析报告》显示，西安市地铁运营线网规模达到123.4 km，日均客运量超过200万人次，线网日平均客运强度达1.91万人次/km，居全国首位。其中，青龙寺站是西安市地铁3号线与5号线换乘的一个枢纽站点，属于地下站，现有一个站厅层和一个站台层。站厅里有2个进站闸机口和2个出站闸机口，其中站台层与站厅层之间有3组楼梯/扶梯连接，分别是西面的上下行扶梯、东面的一个楼梯及一个上行扶梯、站厅中间的直梯和其旁边的上行扶梯。根据客流疏散组合模型来创建西安青龙寺地铁站突发事件下的客流疏散仿真过程。

1) 建立青龙寺地铁站的物理环境仿真模型。设2个列车轨道在站台层，楼梯、扶梯以及直梯是连接站厅层和站台层的通道，除此之外其他要素都属于站厅层(平面图未表现出两层之间的差别)，如图9所示。

图7 行人变道和超越流程图Figure 7 Flow chart of lane change and transcendence

图8 AnyLogic建模过程Figure 8 AnyLogic modeling process

2) 设置仿真模块和仿真参数。结合前面建立的行人客流疏散组合模型和行人移动特征[20]，本文假定地铁行人移动分布服从均匀分布U(a,b)，其中a、b分别是区间(a，b)上的最小值和最大值。在行人生成源中，设置行人到达率为948人/h，行人舒适速度范围为U(1,1.5)，初始速度范围为U(0.3,0.7)，将携带随身物品和行李的旅客直径范围设置为U(0.2,0.3)，故将行人服务中个体延迟时间范围设为U(0.2,0.3)；创建组时，考虑行人结伴而行的因素，将结伴人数设置为2～3人，即U-discr(2,3)，结伴到达率用参数3的对数函数Exp (3/second( ))表示，具体如表1所示。

图9 西安青龙寺地铁站平面图Figure 9 Plane graph of Xi'an Qinglongsi Metro Station

表1 参数设置表Table 1 Parameter settings

3) 客流疏散仿真运行实验。在发生突发事件下，客流疏散过程中每组通道的下行扶梯均已改变为上行方向，进站闸机口全部关闭且出站闸机口全部开放，过程如图10所示。从运行图中看出，部分乘客已经出站，堆积行人最多的地方为通道口。一段时间后，车站内人员全部疏散，此时的状态只剩车站内的必要设施。运行结束后将客流疏散数据导入Excel中进行下一步处理与分析。

3 仿真结果分析

3.1 疏散成功率分析

在仿真中，将人员初始值设置为不同的数值，结果如表2所示。

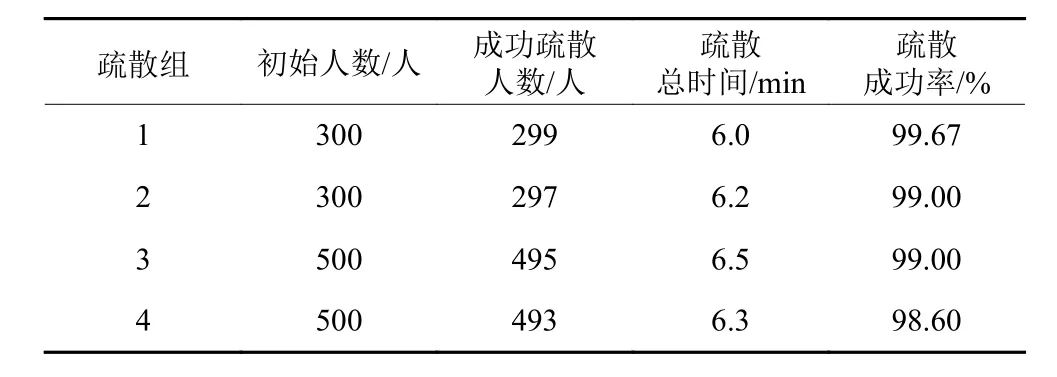
表2 疏散成功率分析表Table 2 Evacuation success rate analysis

从4组数据中看出，疏散初始人数相同时，疏散效率会有不同程度的浮动；疏散初始人数从300增加至500后，人员疏散总时间从最初6 min增加至6.3 min，成功率从99.67%降至98.60%；疏散的初始人数从300增长至500后，疏散效率并无改变(结合客流疏散组合模型，疏散效率一定程度上可维持稳定)。因此，地铁站应对客流量进行预测，并关注大客流产生的时间与状态；在大客流发生时及时对客流进行疏散引导，尽量将疏散效率维持在稳定水平。

3.2 疏散效率分析

当突发事件发生时，个体无法第一时间获知消息，并需要一定的反应时间进行撤离，疏散人数随着时间的变化而变化，最初的疏散效率维持稳定；疏散进行到一定时刻时，由于出口的容量限制，单位时间疏散人员数量将会趋于上限，此时的疏散效率有所降低，如图11所示。可以看到，疏散人数在0～3 min内迅速升至峰值300(以300人为例)。

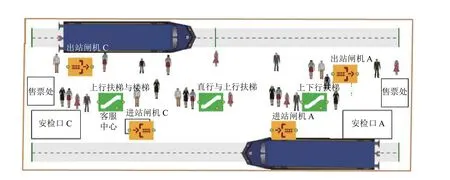
图10 西安地铁青龙寺站客流疏散仿真运行图Figure 10 Passenger flow evacuation diagram of Xi'an Qinglongsi Metro Station

图11 仿真疏散情况Figure 11 Evacuation simulation

3.3 客流拥挤密度分析

从仿真过程可以看出，突发事件发生时，站台层与站厅层之间的通道处会堆积大量的人员，并且出现拥挤现象。而随着疏散时间的推进，站台层的人员逐渐疏散到站厅层，此时2个出站闸机口又会出现堵塞现象。因此，在实际疏散过程中，地铁站须在各个容易出现大密度人群处安排工作人员进行疏散引导，避免人群过度拥挤造成人员伤亡。

4 结论

本文以突发事件为背景，基于元胞自动机理论，建立了地铁客流应急疏散的组合模型，通过AnyLogic模拟，对突发客流情况下应急疏散过程进行了仿真分析。通过分析发现：在突发事件下，疏散人数与疏散成功率成反比，在疏散过程中，初始人数的增加在一定程度上不会降低疏散成功率，同时疏散总时间会随着人数的增大而变长；疏散效率会因环境因素(闸机口，上下行扶梯等)的限制和人流自身因素的变化而变化，疏散到一定时刻，单位疏散人数会趋于上限。同时，本文也分析了站内典型疏散饱和点以及疏散过程中人群主要拥挤点，为西安地铁以及其他城市地铁管理部门制定合理的客流疏散方案提供科学参考与依据。但由于模型中参数的设定需要相关心理研究的理论支撑且有些心理变化无法设定参数，因此之后的研究要梳理心理学研究，精确修正参数，使行人行为更加贴合实际。