双渠道多级分销网络的预防性库存分拨机制与方法研究
2020-07-22郭洪飞李从东黄国全
石 敏,屈 挺,郭洪飞,李从东,,黄国全,4
(暨南大学 1. 管理学院,广东 广州 510632;2.智能科学与工程学院,广东 珠海 519070;3.物联网与物流工程研究院,广东 珠海 519070;4.香港大学 工业及制造系统工程系 中国 香港 999077)
企业在经营过程中为应对不可延期交货带来的缺货损失,往往通过提高库存量降低损失,而这一传统应对方法的弊端在具有多级多销售点的分销网络中显现无疑,大量的库存积压造成了高库存成本,削弱了企业对市场的敏捷性。随着信息网络技术的发展,催生了一种通过减少分销层级,提高销售柔性,增加销售利润的具有规模销售优势的新型销售模式——电商销售,越来越多拥有单一传统/网络分销渠道的零售企业通过增加网络/传统分销渠道,形成了线上线下双渠道的分销模式。企业通过双渠道分销策略实现了挖掘潜在消费群体,提升渠道效率,增加企业利润的目的[1]。而对于具有双渠道的企业来说,同时持有大量线上线下库存反而因高额库存成本削弱了双渠道分销带来的红利优势。面对这一现实问题,有学者指出通过共享多企业多仓库的库存来降低各仓库的库存持有量,实现在保证服务水平的前提下降低库存成本。因此,本文针对双渠道多级分销网络库存系统中不能延期交货的情形,借鉴“库存共享”思想,提出了基于预测时间窗(此时间窗包含在常规补货周期中)库存预测需求量的预防性调拨与预防性补货相结合的“预防性库存分拨机制”,各节点通过预防性库存分拨机制对库存进行控制,对于降低库存成本、缺货损失,提高自身利润水平有重要意义。
具有多个销售周期的产品可以采用预防性库存分拨机制来应对缺货损失。预防性调拨最早由Gross[2]于1 963年提出,是指在客户真实需求发生之前,通过对历史数据的评估进行未来短周期需求的预测,从库存充足的节点向可能发生缺货的节点调运。Tagaras等[3]研究了两级供应链在不同需求分布与库存控制策略下进行预防性调拨的对比分析。Banerjee等[4]提出了基于库存平衡的调拨策略(TIE)和基于库存可用性的调拨策略 (TBA)。Lee等[5]提出了服务水平调整(SLA)。Tiacci等[6]在Minnner的应急性调拨启发式基础上提出了预防性调拨启发式(PTH)。Li等[7]分析了在预测需求与库存之间不匹配的前提下,采用预防性调拨对订购数量的影响。Dan等[8-9]研究了易逝品多销售阶段预防性横向调拨问题。李晓宏等[10]从预防性横向调货的角度研究了多销售渠道企业的库存决策策略。
由于双渠道多级分销网络是一个具有多层级的复杂系统,因此本文采用可以有效解决层级式问题的目标级联分析法 (analysis target cascading, ATC)进行建模求解。凌六一[11]研究了基于ATC的供应链优化设计,证明了ATC解决供应链问题的有效性。Qu等[12-14]通过ATC对多级分散决策的装配供应链进行建模求解,实现分散式决策供应链的优化配置。He等[15]从战略角度出发,通过对ATC迭代模式的修正,解决了竞争与合作两种协调模式。Zhang等[16]在考虑生产负荷与安全库存平衡下,研究集群式两级分布决策型供应链问题,并运用ATC方法对该问题进行求解并验证有效性。
综上,本文针对双渠道多级分销网络库存系统中不能延期交货情形为背景,借鉴库存共享思想对该库存系统的预防性库存分拨机制进行设计,为双渠道多级分销网络低成本高效率的运作提供有效的解决方案。
1 问题描述
1.1 双渠道多级分销网络运作模式
本文考虑1个由零售商集团主导的,销售同质同价产品的双渠道分销模式下的四层级分销网络,如图1所示,该网络的构成节点有4类,分别是集团节点、中心仓节点、区域仓节点及门店节点。其中集团节点为分销网络的最高决策节点,不参与双渠道消费需求的满足,中心仓节点、区域仓节点及门店节点共同构成双渠道分销网络的线上线下渠道。
与分销网络相应的消费需求分为线上消费需求与线下消费需求两类。线上消费需求主要通过2种方式得以满足:1) 由中心仓节点和区域仓节点直接满足;2) 由中心仓向门店进行逐级补货,由门店节点满足线上需求。针对线下消费需求,主要由各门店节点进行满足。分销网络中的各节点包含两类功能。其中,中心仓节点与区域仓节点的功能是对下级节点进行补货并满足分销范围内的线上消费需求;门店节点的主要功能是满足到店的线下需求及门店自提的线上消费需求。因此,各节点库存主要划分为两类:一类是用于满足门店消费需求或向下级节点补货的线下(补货)库存;一类是用于满足线上消费需求的线上库存。

图1 双渠道多级分销网络运作模式Figure 1 Dual-channel multi-echelon distribution network operation mode
1.2 双渠道多级分销网络预防性库存分拨机制
本文的双渠道多级分销网络库存系统在预测时间窗内总体遵循节点内线上线下库存、同层级一对多双向预防性调拨、上下层级间一对一单向预防性补货的库存分拨规则,二者统称为“预防性库存分拨机制”。具体决策过程如下。
1) 预测需求。各节点在周期内固定时间点进行预测,评估未来短周期的需求量。
2) 进行预防性分拨决策。当调拨成本或补货成本高于缺货损失时,计为缺货损失,本文不考虑此种情况。当调拨成本或补货成本低于缺货损失时,优先作出调拨决策(调拨优先级):(1) 节点内线下(补货)库存—线上库存;(2) 同层级节点,同层级调拨时,调拨需求和库存类型不严格对应,即线上库存调拨需求可由同层级节点的线下库存满足;若调拨决策不能满足,则作出补货决策(补货量为线上库存补货量与线下库存补货量之和)。
3) 若为预防性调拨决策,则优先进行节点内线下(补货)库存—线上库存双向调拨,剩余未满足的可能缺货量则通过节点所在的层级调拨;若为预防性补货决策,则在进行节点内调拨后,将剩余未满足的可能缺货量提交上一级节点进行补货。
1.3 模型假设
为简化问题且不失一般性,作出如下假设:双渠道分销网络中所有的节点均采用固定周期盘点策略,即(t,S)库存控制策略,且同一类型节点的盘点周期相同,补货提前期相同;各层级各节点即时需求独立,服从正态分布,预测需求独立;仅考虑一种产品的预防性节点内调拨及同层级调拨、预防性补货过程;调拨为完全共享式,即在满足自身销售需求后将剩余库存全部用于调拨;预防性库存分拨机制中,调拨提前期小于补货提前期;预防性库存分拨机制下的库存分拨运作仅将节点库存补充至期望库存量;节点内调拨时,提前期为0,单位调拨成本为0;同层级调拨选择不超过2个节点协作完成预防性调拨请求。
2 ATC方法介绍
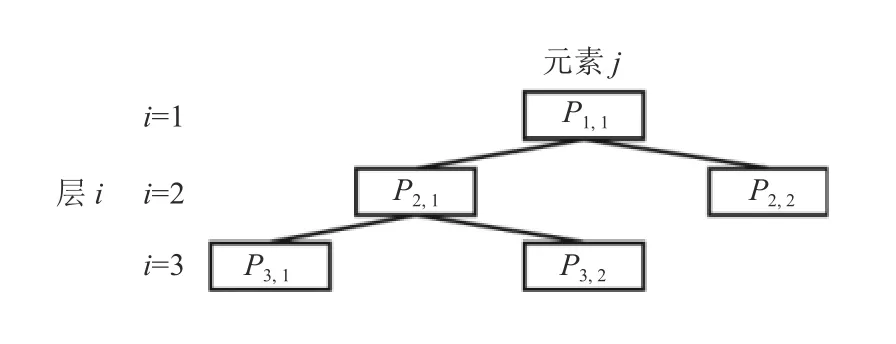
图2 系统结构分层Figure 2 System structure echelon
20世纪末,目标级联分析法(ATC)被广泛应用于复杂系统的优化问题之中,如汽车结构优化和航空飞机结构的优化。其原理是通过对复杂系统进行分层,如图2,其中,i表示层级,j表示元素所在的位置,然后将复杂系统转化为多层级结构的子系统进行优化,通过上级父系统对子系统进行协调优化,最终优化整个系统。
通过ATC方法求解复杂系统的过程共5步,即依据目标分层法、方面分层法或模型分层法对复杂系统进行分层;确定父子层级、子系统同层级的共享变量;建立各层级ATC模型;选择全局的协调求解机制;选择父子系统间协调方法。
ATC方法的优化准则是层级中每个元素将最小化父子之间的共享变量偏差为目标,当所有偏差均在允许的范围内,此时系统可以达到最优状态。具体模型建立及ATC方法求解复杂系统五步骤和模型中符号代表的含义请详见文献[12]。
3 模型构建
预防性库存分拨机制的应用首先是以预测时间窗内的库存预测需求量为基础,其次通过ATC方法进行分拨节点范围、分拨量的确认。因此,本节通过构建需求预测模型与ATC分拨模型双渠道多级分销网络库存的预防性库存分拨机制进行定量化分析。
3.1 需求预测模型
对于销售过程来说,影响消费需求的因素有很多,如市场政策、产品价格和促销活动等。本文的需求预测是对红酒常规补货周期过程中进行的短期时间窗内的需求预测,考虑到研究对象的需求受外界因素和历史前期销售量的共同影响,本文选择建立指数平滑预测模型和多元线性回归预测模型结合的综合预测模型,通过变异系数法确定组合权重。模型建立如下:

其中,τi为每个单一预测模型的权重;est为第t期的指数平滑预测模型预测值,est−1为第t−1期的指数平滑预测模型预测值,rt为第t期回归模型的预测值,Dt−1为第t−1期实际需求量;α为平滑系数;β0、β1、β2、β3为待计算回归系数;xt,1、axt,2、pxt,3为第t期产品价格、替代品价格变化率、节假日促销价格3个主要因素;π为随机干扰因素且服从(0,σ2)的正态分布。对于模型中权重的确定,根据每个单一模型确定的预测值,从而计算每个单一模型预测值的平均值和标准差 σi,进而求得每个单一预测模型的变异系数vi=σi/,i=1,2。其次,对每个单一预测模型的变异系数进行归一化后得到的数值就是每个单一预测模型的权重虽直观上存在权重大而且预测结果不准确,但根据文献[17]可以看出,组合模型的准确性高于指数平滑法预测和多元回归模型预测的结果。
3.2 预防性库存分拨模型
在对需求预测模型的结果和实时库存运行状态进行精准识别和综合评估的基础上,构建在预测时间窗内的关于节点分拨决策、节点范围及分拨量的ATC预防性分拨模型。
按照ATC的结构和建模思路,本文将双渠道多级分销网络下的库存预防性分拨问题分为3层,如图3所示,分别是中心仓层、区域仓层和门店层。各层级的决策变量为调拨量分配比例d和分拨需求服务时间ST,而ST也是系统的共享变量。三层级的目标均是运作成本和分拨需求服务时间最小,且运作模式均为优先进行节点内或同层级间进行调拨,当需求不满足时触发预防性补货机制,因此下述各层级模型大致相同。
模型所需参数符号说明如表1。下标e表示线上,s表示线下,t为调拨,h为库存持有,b为缺货,r为补货。TC表示总成本,c为单位成本。
3.2.1 中心仓层库存分拨模型


图3 双渠道多级分销网络转化ATC层级系统图Figure 3 Dual-channel multi-echelon distribution network transforms ATC level system

表1 参数符号说明Table 1 Description of parameters and symbols


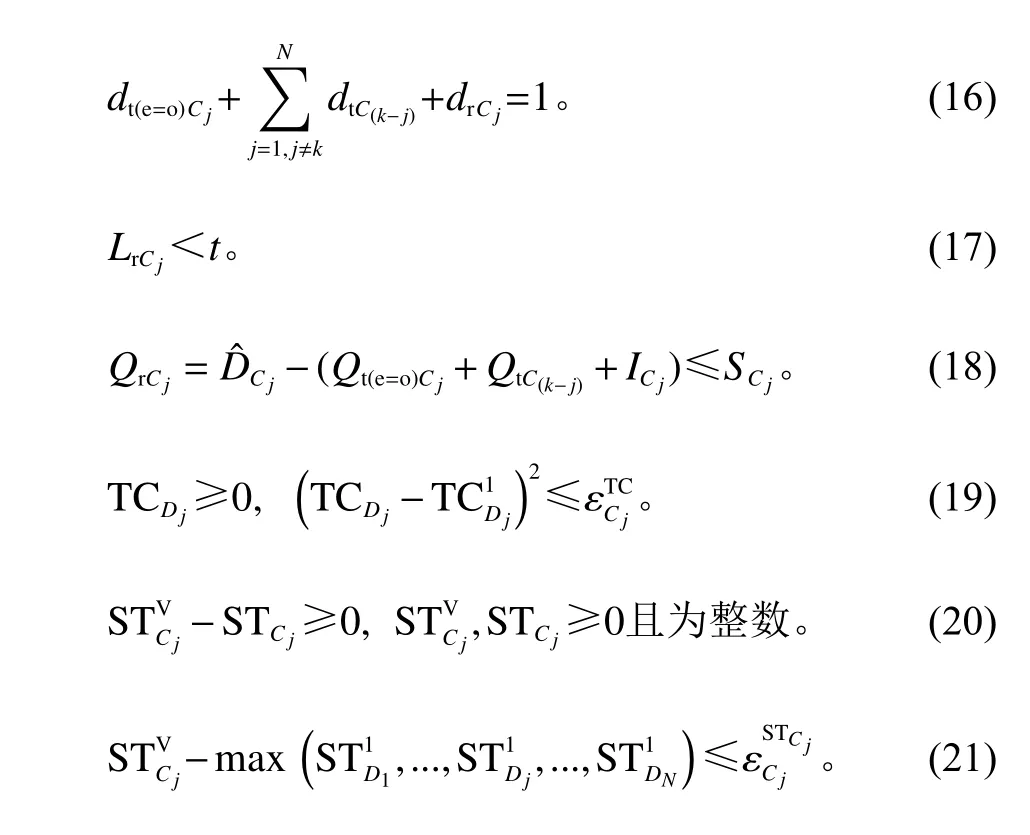
中心仓层节点的ATC模型中,式(2)为中心仓层最小化目标函数,其主要由该节点的运作总成本、调拨服务时间及与成本一致性偏差和服务时间一致性偏差组成;式(3)为节点运作总成本与下游节点总成本TCDj之和,节点运作成本包括式(4)的库存持有成本、式(5)的节点库存转运成本、式(6)的预防性补货成本及式(7)的缺货成本;式(8)为节点输入输出的服务时间;约束(9)分别为节点内调拨比例约束、节点间调拨比例约束及预防性补货比例约束;约束(10)为是否需要同层级调拨判断;约束(11)为节点满足同一调拨请求的所有比值总和为1;约束(12)为满足同一调拨请求的节点不超过2家;约束(13)为调拨提前期小于补货提前期;约束(14)、(15)为判断节点是否进行预防性补货;约束(16)为节点内调拨、同层级调拨预防性补货的比值总和为1;约束(17)为预防性补货提前期小于固定盘点周期;约束(18)表示预防性补货的补货量以预期需求量为准,数量不超过基本库存水平;约束(19)—(21)为一致性偏差约束,保证所有的底层关键联系都在容限变量范围内。
3.2.2 区域仓层库存分拨模型


在区域仓层节点的ATC模型与中心仓层节点的模型相似,因此公式表示的具体含义可参见中心仓层节点,在此不进行重复。
3.2.3 门店层库存分拨模型
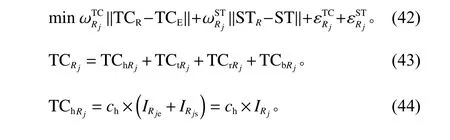

中心仓层作为层级式ATC结构的最底层,并没有下游阶段,所以目标函数不存在一致性偏差项,其余公式及约束的含义与中心仓层节点相似,可参见中心仓层节点的模型解释。
3.3 ATC模型求解机制
对ATC模型的求解涉及两个方面:1) 确定ATC的全局协调机制,即ATC的收敛顺序;2) 确定每层模型中各子元素的局部优化。如文献[12]中的介绍,本文选择权重更新法作为全局协调策略。而近年来,遗传算法在供应链优化领域的应用越来越广泛,因此本文也选择遗传算法进行层级子模型局部的优化。其中,通过序列结合的方法对各节点染色体编码;适应度函数选择目标函数;用精英选择与适应值比例相结合的方法确定选择算子;通过两点交叉进行生成交叉算子。
4 数值分析
以国内某大型进口红酒贸易企业的实际分销过程为例来验证模型的有效性。该大型进口红酒贸易企业具有实体门店和网络销售两种分销方式,本案例中的双渠道多级分销网络由18个节点构成,分别是中心仓节点3个、区域分销仓节点5个、门店节点10个。分销网络中同类型节点的单位补货成本、持有成本、调拨成本、缺货成本相同。相关具体参数见表2。
ATC模型求解过程初始参数值设定如表3所示。
各层级模型遗传算法初始参数值设定如表4所示。
对于ATC模型求解部分,选择底层先收敛作为全局协调策略,采用遗传算法进行每层级节点局部优化。选择AIO(all in once,传统一体化优化算法)和ATC协调这两种算法对该问题进行求解,以AIO求解的结果作为参考,测试ATC对求解此类问题的有效性。
由表5可以看出,本文所使用的ATC优化算法与AIO优化算法在求解结果准确性上一致,证实了ATC在求解通过库存预防性库存分拨机制优化双渠道多级分销网络库存成本的有效性;从运作成本总计栏可以看出预防性库存分拨机制下的运作总成本明显低于不采用预防性分拨的总成本;从优化时间可以看出ATC优化的速率低于AIO的优化速率,这是因为ATC优化过程需要将系统分层,层级间具有复杂的耦合关系。
需求的方差变化影响需求波动,而需求波动对双渠道多级分销网络的预防性库存分拨机制影响较大。本节以区域仓层节点3为例,其需求方差从50~200变化,分析需求波动对有无预防性库存分拨机制有效性的影响。结果如图4。
由图4可以得到,需求方差越大,需求波动越明显。随着需求方差的变大,节点无论是否采用预防性库存分拨机制,运作总成本均呈现相同的变化趋势;对比不同需求方差下有无预防性库存分拨机制的运作成本,可以看出随着需求波动越大,采取预防性分拨后的运作成本低于无预防性库存分拨机制下的运作成本,且差值逐渐变大。
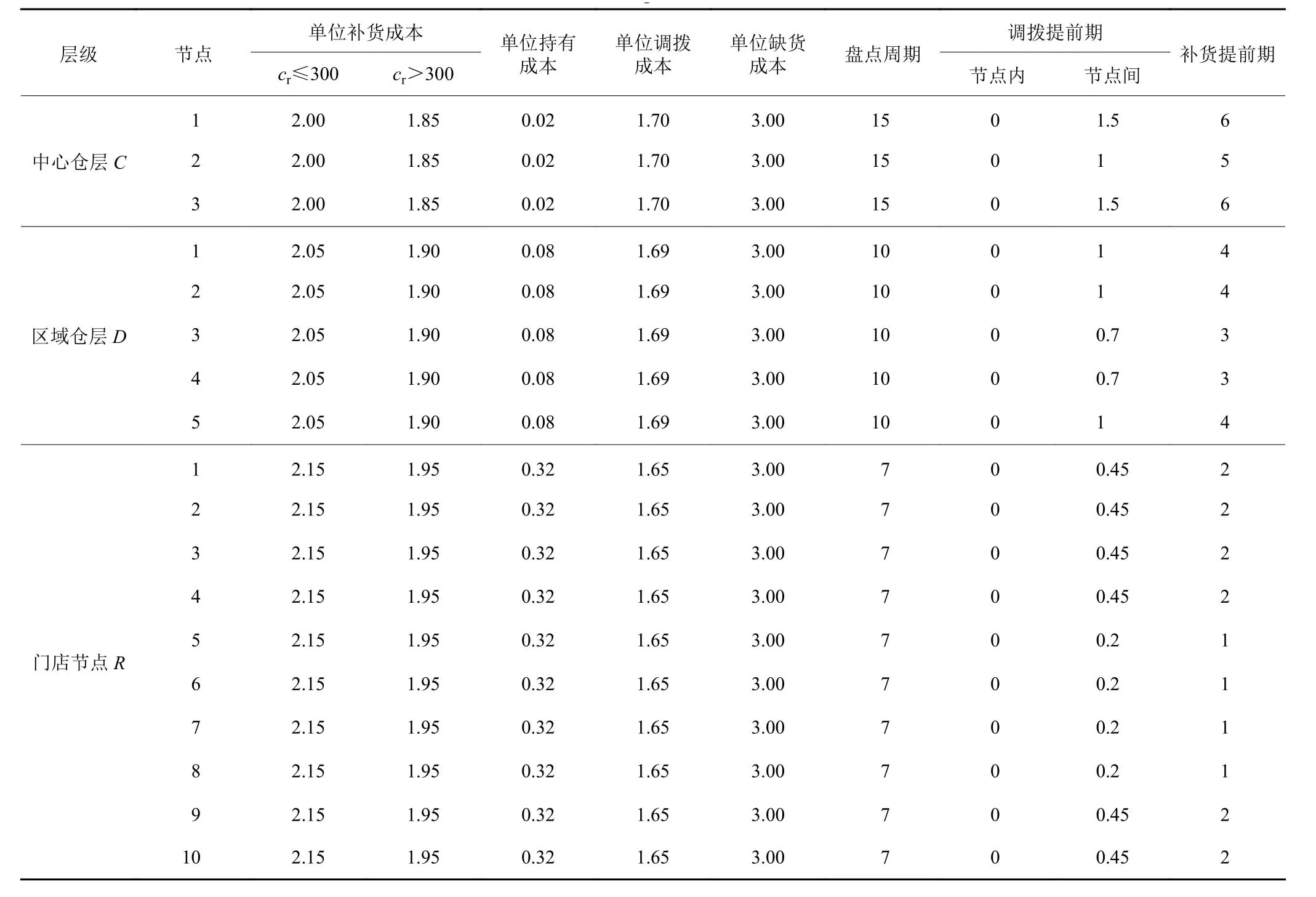
表2 案例具体参数Table 2 Case parameters value
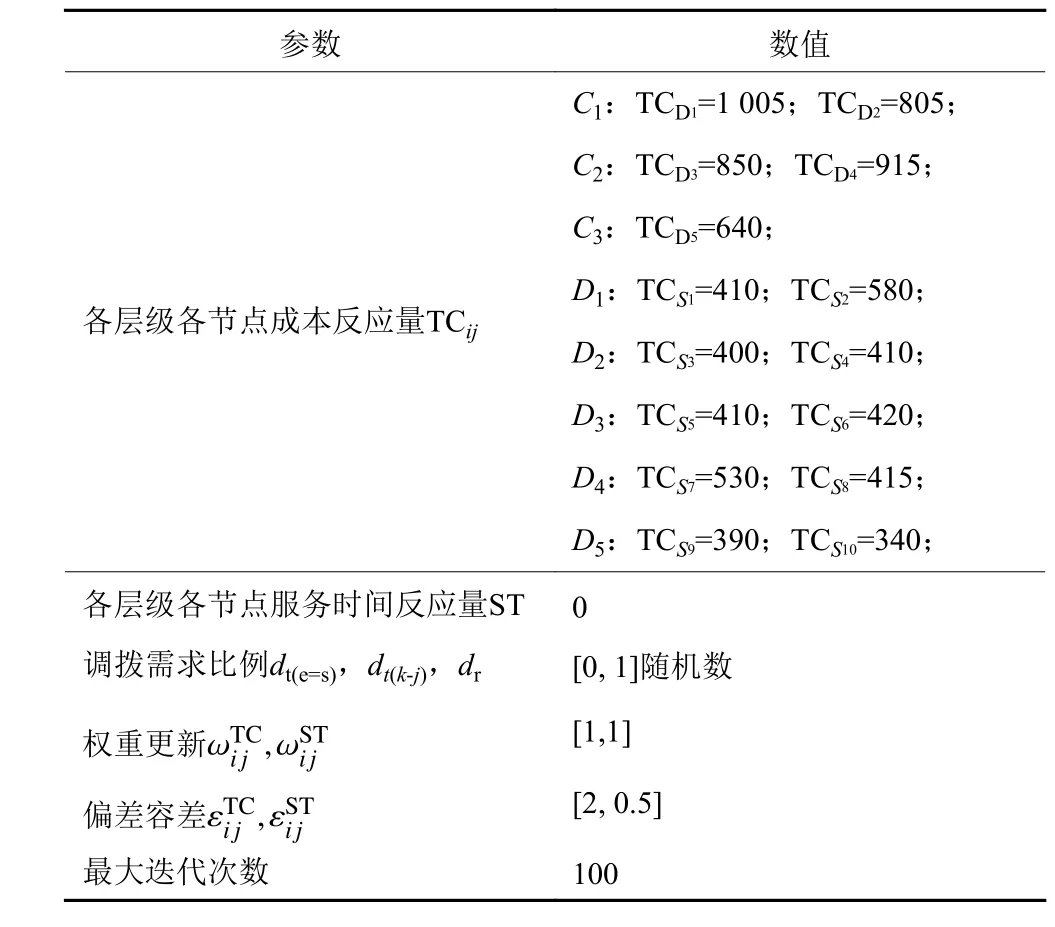
表3 ATC模型协调求解初始参数值Table 3 ATC model coordination solve initial parameter values

表4 层级模型遗传算法初始参数值Table 4 Genetic algorithm initial parameter value of echelon model
5 总结
本文研究了双渠道多级分销网络环境下不可延期交货的情形下,提出了预防性库存分拨机制——基于节点内线上线下库存、同层级一对多双向预防性调拨、上下级间一对一单向预防性补货运作规则的预防性库存分拨机制,并通过ATC构建多学科优化的多层级协调优化模型,对相关重要参数进行了敏感性分析。从敏感性分析的结果中可知,需求波动越大,预防性库存分拨机制的效用越明显。当企业的需求波动较平稳时,是否采用预防性分拨对运作成本的影响不显著;当需求波动幅度较大时,企业可以选择采用预防性分拨策略以保证节点的服务水平,增加销售利润。

表5 ATC优化结果与AIO优化结果对比Table 5 Comparison of ATO optimization results and AIO optimization results
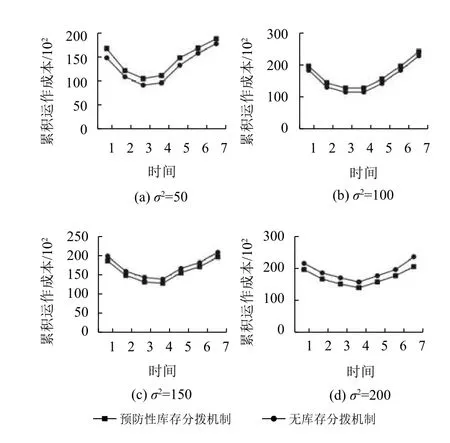
图4 需求波动对预防性库存分拨机制有效性的影响Figure 4 Effect of demand fluctuations on the effectiveness of the preventive inventory allocation mechanism
