基于博弈论的两级逆向供应链定价策略研究
2020-07-22石永强王佳欣张智勇
石永强,王佳欣,张智勇
(华南理工大学 经济与贸易学院,广东 广州 510006)
定价是对投入要素的一种价格反映,也是追求利润的需求,同时更是协调市场营销决策、企业竞争策略和财务决策以实现企业盈利的一种战略性行为。供应链定价策略是全面研究和应用供应链渠道伙伴关系合作与协调理论的重要补充,因此,国内外诸多学者皆对供应链定价问题开展了研究。孔造杰等[1]针对零售商开辟电子商务双渠道供应链的定价模型进行了研究。陈卫华等[2]结合资金约束和供应链成员的风险态度研究了双渠道供应链的定价策略。但斌等[3]研究了服务水平对产品服务供应链的定价影响。
随着社会的发展,环境的要求,资源的可持续有效利用,现在许多产品制造商会从市场回购废旧产品对其进行有效的拆解进行加工再生产,从而出现了逆向供应链。对此,学者对供应链定价的研究也从传统的供应链发展到逆向供应链。Majumder等[4]用博弈理论研究了逆向物流的最优定价决策的制定。孔令丞等[5]利用合同理论的方法,借鉴类似回购合同的假设,研究“制造商−零售商”二级供应链中不同质量水平的产品回收最优定价问题。顾巧论等[6]基于单一制造商和单一零售商构成的逆向供应链系统,应用博弈理论对废旧产品回收的定价策略进行研究。舒亚东等[7]考虑一个再制造商和两个竞争性回收商组成的逆向供应链,研究回收商之间竞争强度以及回收商的公平关切程度对逆向供应链定价决策的影响。
在供应链定价决策的研究中,Stackelberg博弈模型是一种较为常见的模型,周亚军[8]引入了一致定价策略,构建了供应链Stackelberg博弈模型,研究了分散式和集中式双渠道供应链中考虑产品退货因素的最优定价与服务决策问题。Liu等[9]同样使用Stackelberg博弈模型实现顾客退货条件下的供应链定价和零售商服务水平决策。祝凌燕[10]研究了制造商和零售商依据生产成本和行业平均利润加成定价的闭环供应链优化问题。孙多青等[11]用博弈模型解决了多个零售商参与下的逆向供应链中的定价策略,同时利用K-S法解决合作利润分配问题。
上述文献的研究各有侧重点,但是在对逆向供应链的定价方面,主要是将回购数量设置为回购价格的线性函数。而现实中很有可能会是非线性函数。因此,本文选择用幂函数来模拟回购曲线,研究1个制造商和1个零售商的二级逆向供应链的定价问题。本文先详细描述研究问题并作相关假设;再通过建立分散式博弈定价决策与合作博弈的对比模型得到一些有现实意义的结论;最后通过算例分析进行验证。
1 问题及假设
1.1 问题描述
本文研究对象是1个制造商和1个零售商的二级逆向供应链,制造商委托零售商向消费者回收废旧产品,由制造商重新生产加工,再卖回到消费者市场。在回收废旧产品的逆向供应链中,零售商以1个回购价格从消费者手中回收一定数量的废旧产品,回收后将废旧产品以制造商给出的回购价格卖回到制造商手中,在零售商回收的过程中存在运营成本,制造商重新生产加工废旧产品也需要一定的再生产成本。
1.2 基本假设
1) 废旧产品的回收量是与回收价格有关的幂函数,回收价格越高回收量越大;
2) 制造商将全部回收零售商手中的废旧产品;
3) 制造商回收的废旧产品能够全部重新生产加工并卖出,不会有剩余。
1.3 符号说明
P为制造商将再生产产品卖回市场的销售价格;
Pm为制造商回收产品的回收价格,是制造商的决策变量;
Pr为零售商回收产品的回收价格,是零售商的决策变量;
Cm为制造商对回收产品再生产的生产成本;
Cr为零售商回收产品的单位边际运营成本;
Q为零售商从市场回收的产品量,是一个幂函数,满足其中k、λ是常数,k>0,0<λ<1;
r为零售商的边际利润率,影响零售商的回收价格;
πm为制造商的利润函数;
πr为零售商的利润函数;
π 为供应链的总利润函数。
2 模型构建
2.1 非合作博弈模型
非合作博弈又称分散式决策,即制造商和零售商各自制定决策,确定回购价格。在本文所研究的问题当中,制造商规模较大且较为强势,因此本文选择的是制造商为主导的Stackelberg博弈模型。在此种情况下,制造商在供应链中占主导地位,零售商为跟随者,存在反应函数,制造商会根据零售商的反应函数找出使其利润最大的产量。制造商为了使自身利润最大化,将产品以最优的价格从零售商处回收;然后处于从属地位的零售商根据制造商制定的回收价格来确定自己最优的对客户的回收价格以及回收数量,以达到自身利润最大化的目的。
首先,根据问题描述,可以定义以下函数式。
零售商的回收价格函数

零售商的回收数量函数
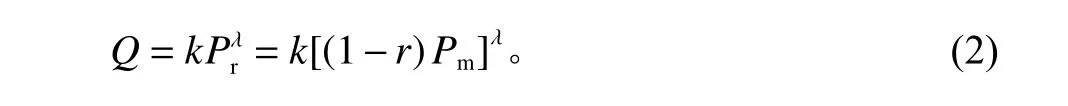
制造商利润函数和零售商利润函数分别为
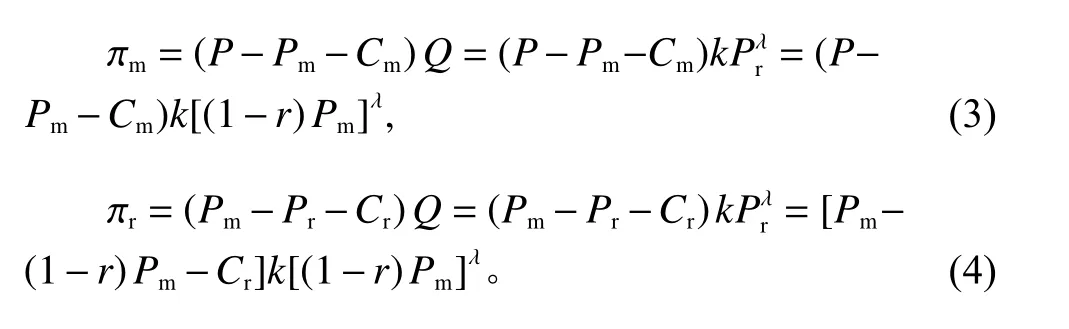
用逆向归纳法求解。先考虑零售商最优的订价策略。将零售商的利润函数对边际利润率r求偏导数

令式(5)为0,可以求得r关于Pm的反应函数

可求出零售商回收数量的数量函数式
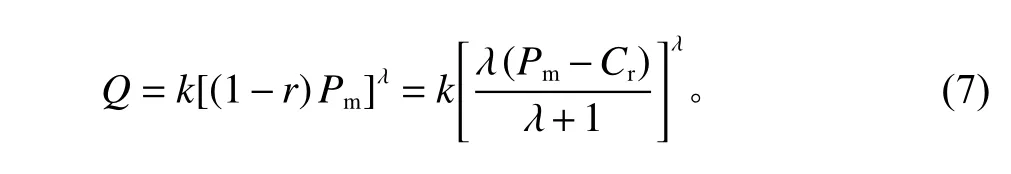
将式(6)、(7)逆向代入式(3),可以得到制造商在认为零售商是跟随者的情况下重新计算的利润函数:
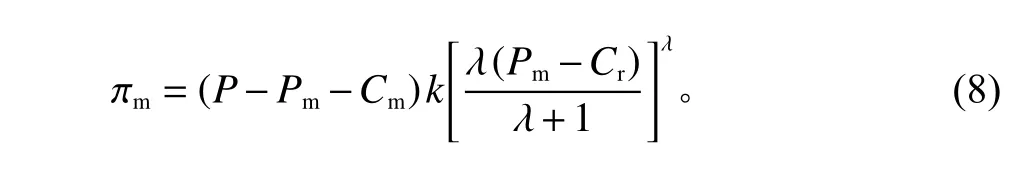
将其对Pm求偏导得

令式(9)为0,得到制造商最优回收价格
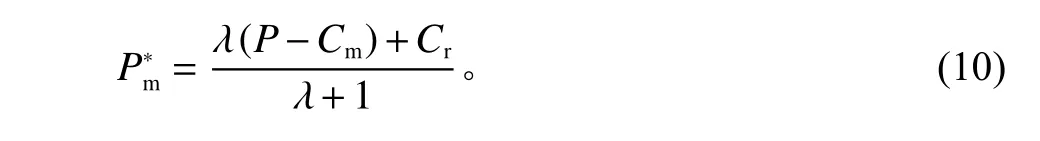
将式(10)代入到式(6)可以得到

将式(11)代入式(1),最终可得零售商的最优回收价格为
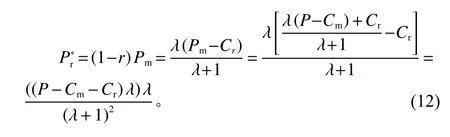
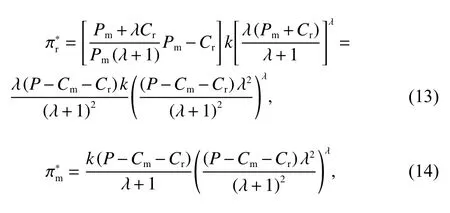
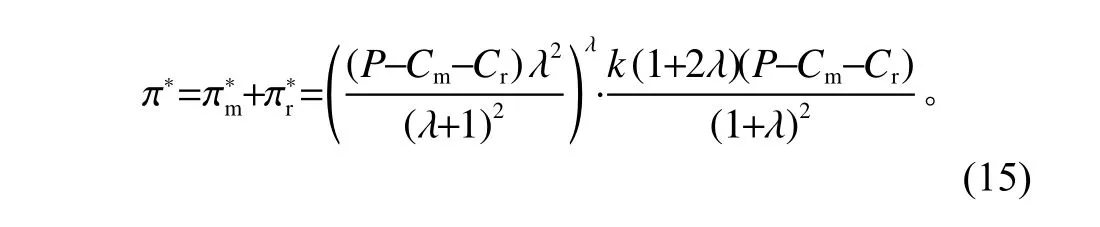
2.2 合作博弈模型
合作博弈模型又称集中式决策。在合作情况下,制造商和零售商在信息共享基础上考虑系统总体收益的最大化。实现合作的前提是:合作时系统的总收益大于不合作时参与成员的收益之和。并且,供应链系统中各成员都不会有损失,否则成员就会退出合作。因此需要很好的契约来对利润进行重新分配。
2.2.1 模型构建
合作时,参与成员结成联盟,该联盟通过价格手段实现自身收益,即制造商和零售商联合制定回收价格,以最大化系统的利润。这时,逆向供应链系统整体利润函数的表达式为
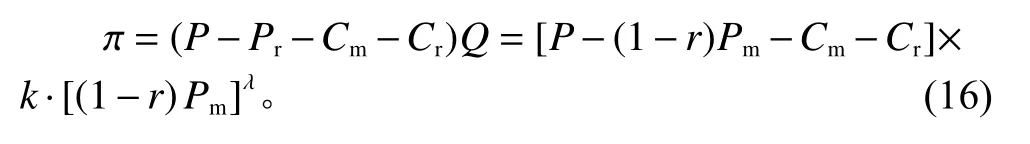
为了求供应链利润最大化问题,可将问题转化为求解下列方程组
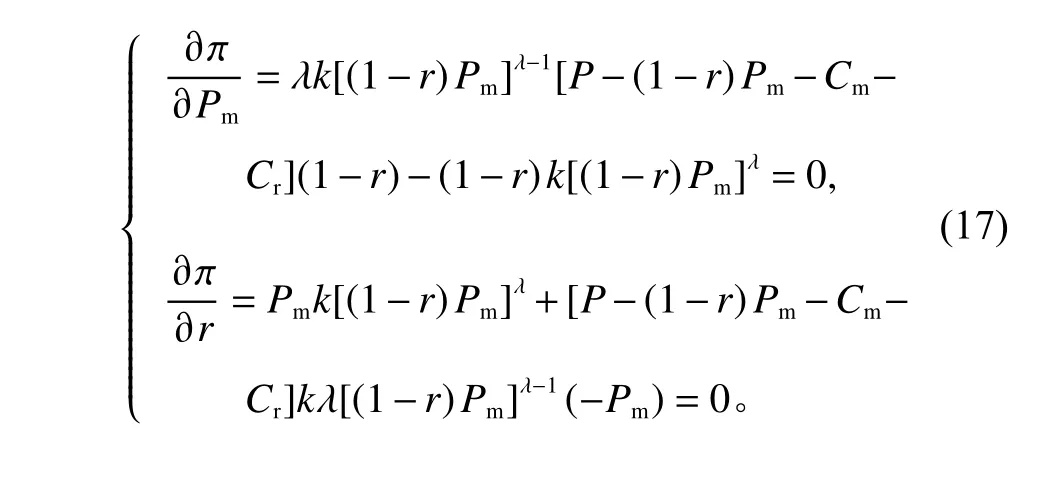
通过式(17)可以得到
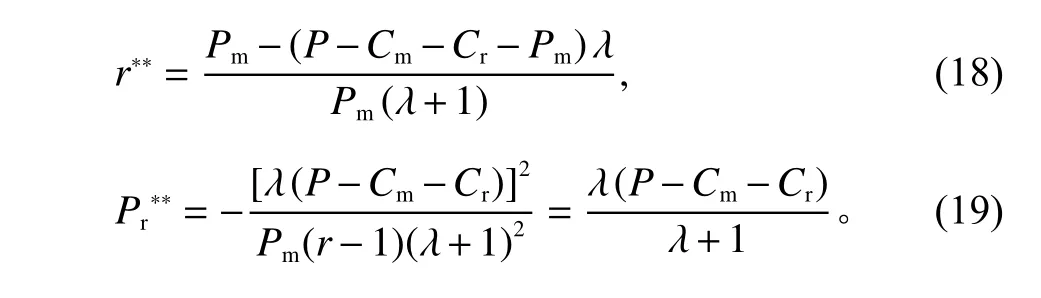
将式(17)、(18)、(19)代入式(15)中,可以得到供应链总利润的表达式

即

定理1合作博弈的供应链总利润要大于制造商主导的非合作博弈的供应链总利润,且利润差额为
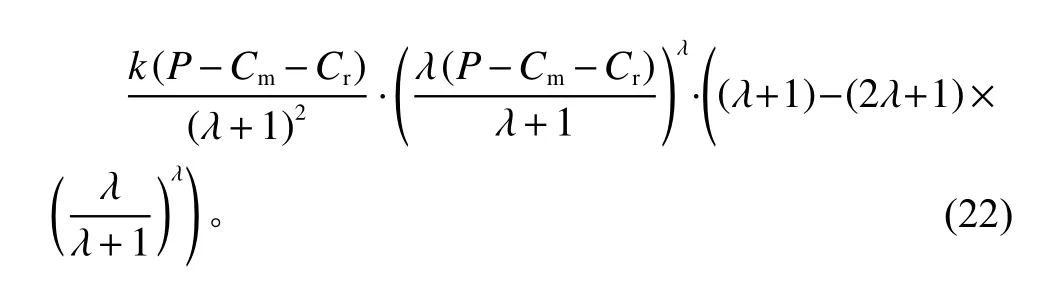
证明
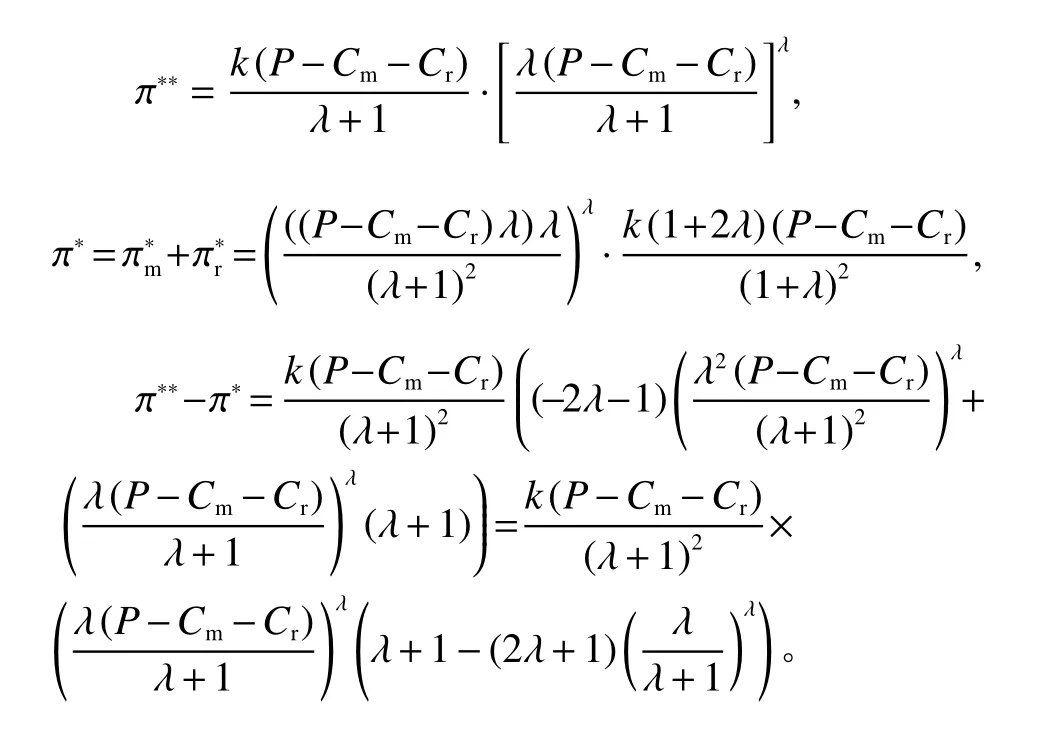
由于P>Cm>Cr,k>0,0<λ<1,易知现需证明对此,设f=λ+1−(2λ+1)×借助计算机软件(Maple 2 016)可以得到当0<λ<1时的函数图像(如图1),图1可以清晰地观察到,在0~1的范围内,函数f为单调递增,所以f>f(0)=0,因此,当0<λ<1时,必然大于0。
综上可证,π**−π*>0。
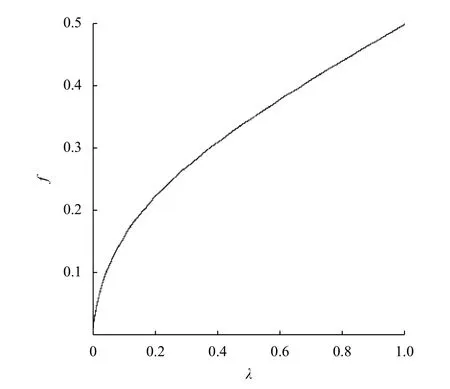
图1 函数 f图像Figure 1 The graph of function f
定理2合作博弈供应链的零售商回收价格要高于制造商主导的非合作博弈的供应链中零售商的回收价格,卖出废旧产品的客户获益更多。其差额为

证明:
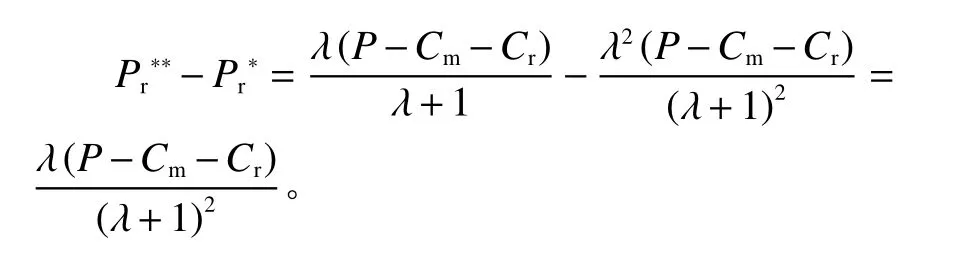
2.2.2 合作博弈利润分配
本文采用了Shapley值法来实现1个制造商和1个零售商的二级逆向供应链合作定价时的利润分配问题。Shapley值法是一种所得与其对联盟的边际贡献期望值相等的分配方式,普遍用于经济活动中的利益合理分配等问题。在Shapley值法中,合作方所得利益分配值被称为Shapley值,表示为
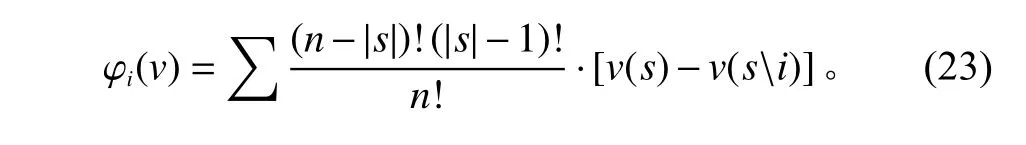
其中,n为供应链上的成员个数;s为若干成员合作的子集,|s|为其中成员的个数;v(s)为子集s产生的效益;v(si)是子集s中除去企业i时产生的效益。
本节研究的是1个制造商和1个零售商之间合作博弈的利润分配问题,因此在联盟中仅有两个合作方,制造商和零售商各自对联盟的贡献率分别为

现需计算出制造商和零售商不进行合作下的Shapley值,以及合作下的Shapley值,然后加权求和。
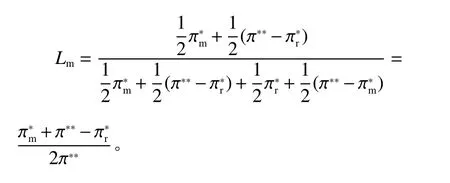

表1 制造商的分配利益φ m(v)计算表Table 1 Calculation table of manufacturer's distribution benefit φm(v)

表2 零售商的分配利益φ r(v)计算表Table 2 Calculation table of retailer's distribution benefit φr(v)
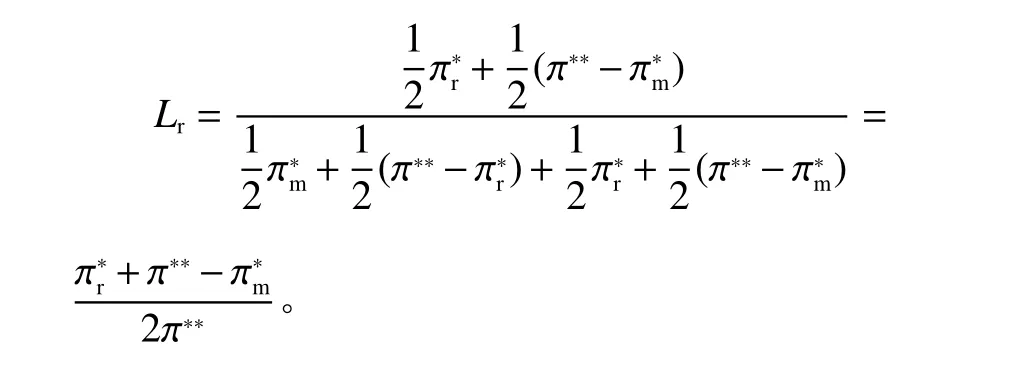
3 算例验证
根据本文研究的问题描述,设案例参数如表3所示。

表3 案例参数Table 3 Parameters in case
将上述参数代入模型中求得制造商主导的非合作博弈以及合作博弈下的均衡结果如表4所示。

表4 非合作博弈与合作博弈时的均衡结果Table 4 Equilibrium results in non-cooperative games and cooperative games
由表4可以看出,在1个制造商和1个零售商构成的两级逆向供应链中,双方合作定价的情况下能够提升整个供应链的总利润,这使供应链成员之间的合作存在可能性。通过适当的利润分配契约,能使因合作多出的利润分配到各成员之间,如本文使用的按贡献度分配法,使各成员都获得了比非合作博弈更多的利润,因此,逆向供应链的合作将继续进行下去。此外,从表中还可以看到,合作博弈下的回收价格要高于非合作博弈下的回收价格,这说明卖出废旧产品的消费者将从回购中获得更多的好处。
同时,为了检验模型的准确性,本文借助Matlab R2 014a进行仿真,依次改变参数中的某个参数,可以得到如图2、图3所示的结果。
从图2可以看出,当回收量对回收价格的反应更为激烈时,供应链总体期望利润会增加;当制造商将再生产产品重新投放市场的价格P越高,供应链总体期望利润也更高;当逆向物流某个环节的成本增加,包括制造商再生产的成本Cm和零售商回收单位边际运营成本Cr,整个供应链的利润将会有所下降。但是,无论在何种参数变化之下,合作博弈模型获得的供应链总体收益仍然要高于非合作博弈下的供应链总体收益,此种结论恰好验证了定理1。
从图3可以看出,再生产产品市场价格P、制造商再生产的成本Cm和零售商回收单位边际运营成本Cr能够引起零售商回收价格的变化,容易看出,合作博弈模型的零售商回收价格要明显高于非合作博弈下的回收价格,这一结果也恰好验证了定理2。
4 结束语
逆向供应链的研究有助于增加资源的有效利用,减小资源环境压力,同时减少废物的污染,促进社会的循环可持续发展。研究供应链定价有助于提升供应链的整体效益,以提高整个系统在行业中的竞争力,也能保证各成员获利。本文运用博弈论的相关知识,针对现实中的制造商委托零售商回收废旧产品以再次加工的逆向供应链定价问题展开研究,分别构建了制造商主导的分散式定价模型和合作博弈的集中定价模型,从理论和算例上证明了合作博弈能够给供应链带来更多利润,成员也能分别获得超出不合作的利润,与此同时,合作博弈下的废旧产品回购定价要更高,这样也能让消费者获益。

图2 参数变化对供应链利润的影响Figure 2 Effect of parameter changes on profit
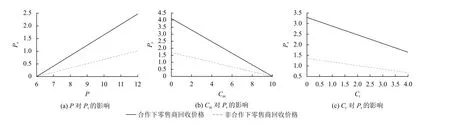
图3 参数变化对零售商回收价格的影响Figure 3 Effect of parameter changes on retailer recycling prices
