基于梯度法的PN结数值计算

任洪波，孟令辉

基于梯度法的PN结数值计算

任洪波，孟令辉

（衡水学院 电子信息工程学院，河北 衡水 053000）

描述半导体PN结特性的方程为一组非线性方程，又称为泊松方程。梯度法是一种有效求解非线性方程的数值方法，将其应用于求解实际的物理问题，如PN结特性方程，有助于加深对物理概念的理解。推导了梯度法的一般原理，并通过将泊松方程线性化，成功应用梯度法求解了PN结的内建电场，电位，平衡载流子浓度等参数沿结方向的分布。进一步研究了外加偏压和掺杂浓度等参数对PN结特性的影响。数值结果表明，采用梯度法求解玻尔兹曼方程比牛顿迭代法精度更高。梯度法在求解非线性方程组所描述的半导体PN结问题上是可行的。

半导体；PN结；梯度法；数值计算

随着集成电路的规模越来越大，对半导体行为的仿真计算也变得越来越重要。半导体所遵循的方程组一般由泊松方程、电荷连续性方程等方程组成。其中，泊松方程为一组非线性方程，在求解时需要采用数值方法将其线性化再求解，一般采用牛顿迭代法进行处理[1]。泊松方程反映了PN结中个坐标处电势分布与电荷密度的关系，在整个求解过程中至关重要。在PN结的求解中一般选取电势、载流子浓度、作为变量[2]。一般采用有限差分法通过差分方程替换偏微分方程的方式，得到各变量间的函数关系，给定一组初值和边界条件进行迭代求解[3]。这样就把求解PN结的电势、载流子浓度的物理问题转变成了求解方程组根的数学问题。笔者研究了梯度法求解非线性方程组的可行性，并将其应用于求解PN结中各参数分布。数值结果表明，采用梯度法求解PN结特性方程，方便简单，精度更高。文中求解了突变结的电势、电场及载流子浓度随坐标变化趋势，研究了外加偏压及载流子浓度对PN结的影响，数值结果与理论分析一致。

1 梯度法的一般原理

梯度法又称最速下降法，通过构造指标函数，求解指标函数极小值，使函数从初始值沿梯度下降的方向逼近真值。

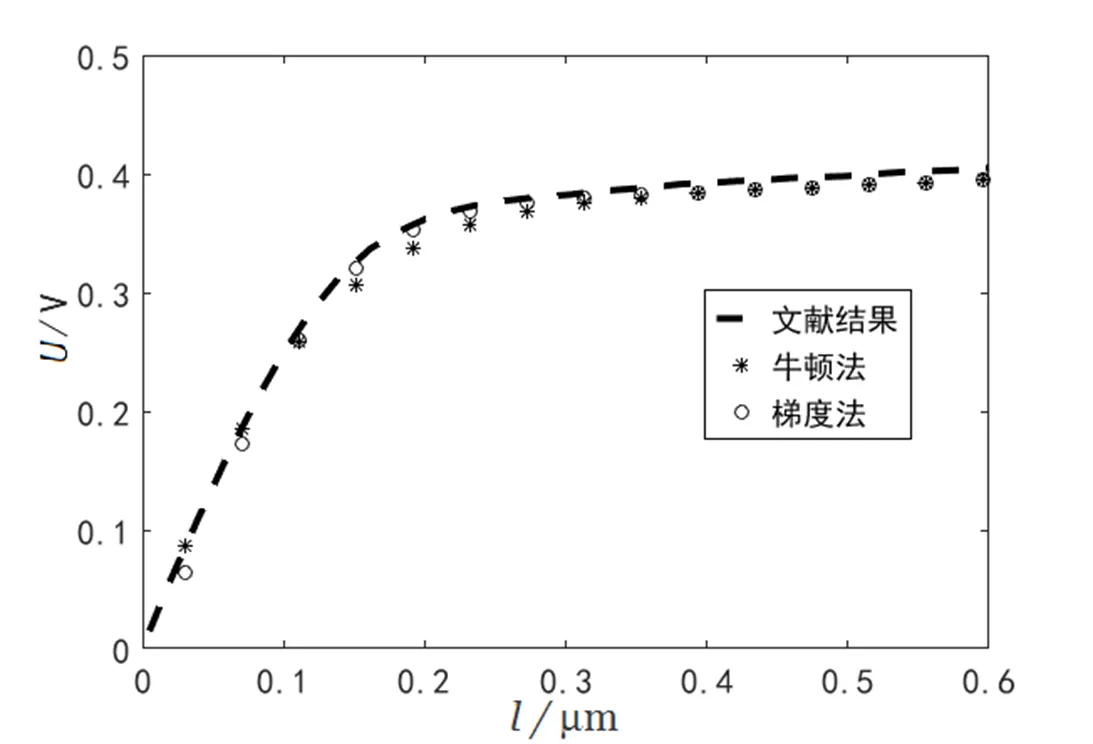
图1 线性缓变结电势分布

图2 平衡载流子浓度分布

2 突变结梯度法分析

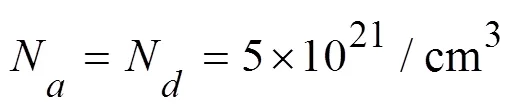
图3 取不同偏压时电势分布

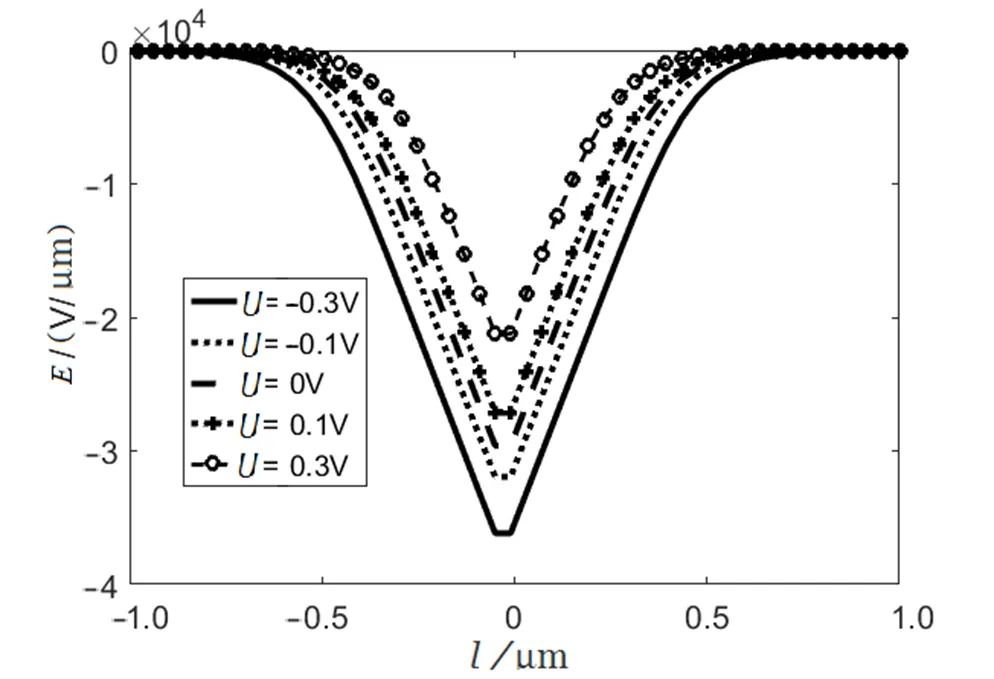
图4 取不同偏压时电场分布

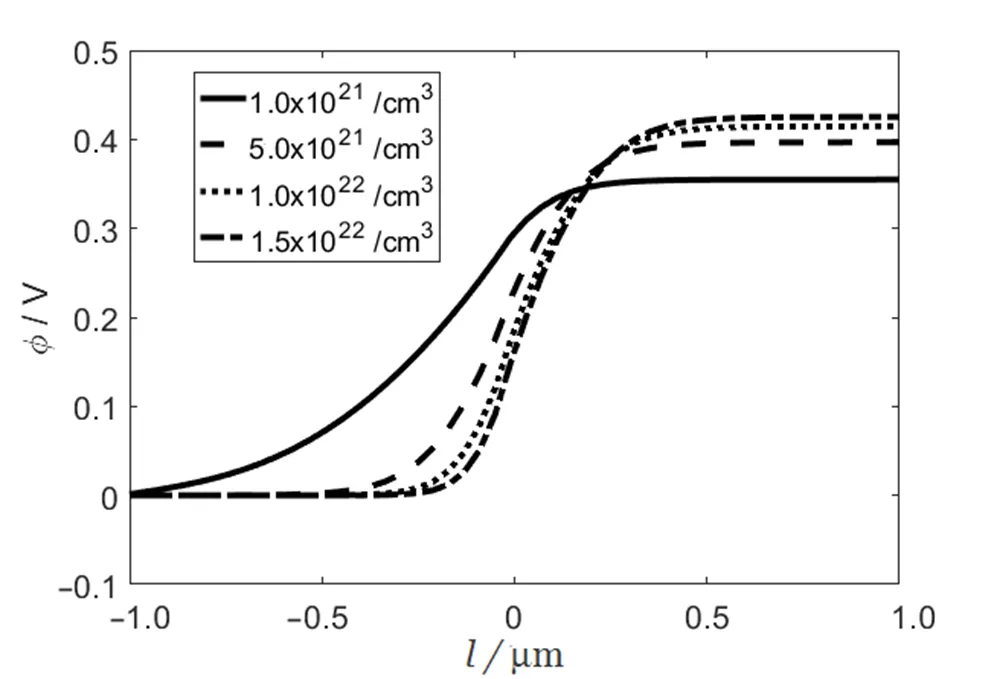
图5 掺杂浓度对电势的影响

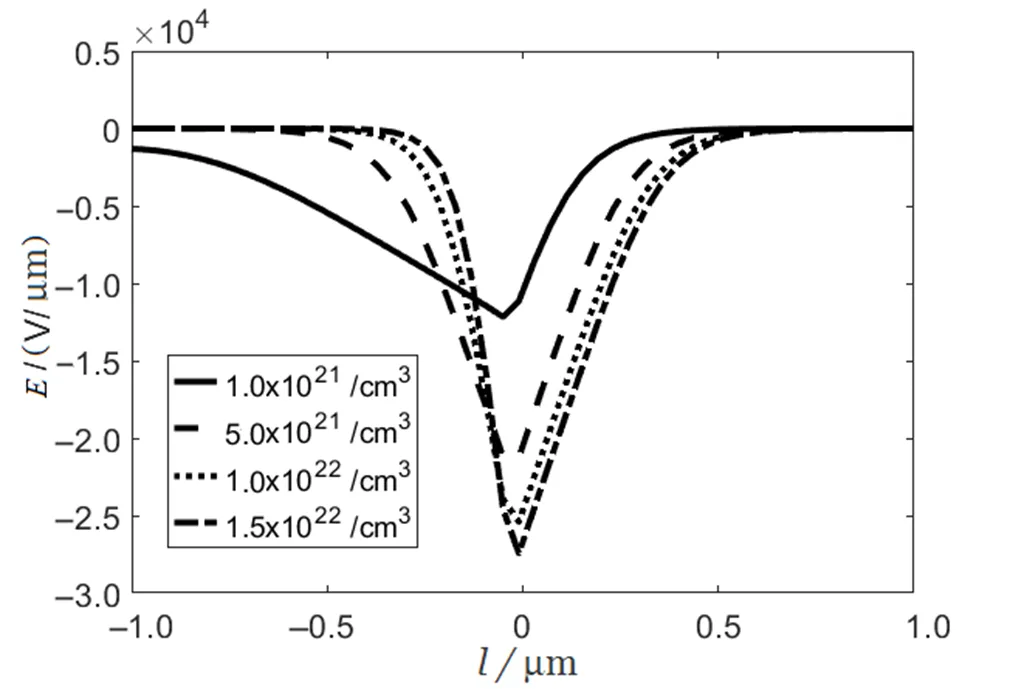
图6 掺杂浓度对电场的影响

3 结语

陈述了梯度法求解非线性方程组的数值方法，并将其应用于求解PN结的泊松方程，得到了与文献相同的结果，表明该方法的正确性。通过该方法研究了不同掺杂浓度和不同偏压情况下PN结的电势、电场等参数随空间坐标的变化趋势。结果表明，掺杂浓度较低时电势变化较缓和，平衡电势也相对较小，空间电场也相应降低，反之则升高。当存在正向偏压时，空间电荷密度降低，电势降低；存在负向偏压时，空间电荷密度增加，电势升高。数值结果与理论分析一致，反映了PN结参数的空间变化情况。

[1] 邓宏贵,郭俊,刘利强,等.PN结泊松方程的一种改进算法及其Matlab验证[J].中南大学学报(自然科学版),2008,39(5):913-917.

[2] 仓田卫.半导体器件的数值分析[M].北京:电子工业出版社,1985.

[3] 丁扣宝,潘骏.利用I-V正向特性提取PN二极管主要参数的研究[J].电子器件,2002,25(1):27-28.

[4] 赵鸿麟.半导体器件计算机模拟[M].天津:天津大学出版社,1989.

Numerical Simulation of PN Junction Based on Gradient Method

REN Hongbo, MENG Linghui

(College of Physics and Electronic Information, Hengshui University, Hengshui, Hebei 053000, China))

The equations describing the characteristics of semiconductor PN junction is a group of nonlinear equations, called Poisson equation. Gradient method is an effective numerical method for solving the nonlinear equations. Applying it to solving practical physical problems, such as the characteristic equation of PN junction, is conducive to deeply understanding the concept of physics. Firstly, the general principle of gradient method is deduced. By linearizing the Poisson equation, the gradient method is applied successfully to solving the distribution of the built-in electric field, potential, equilibrium carrier concentration and other parameters. The effects of external bias voltage and doping concentration on PN junction were also investigated. The numerical results show that the gradient method is feasible in solving the problems of PN junction.

semiconductor; PN junction; gradient method; numerical calculation

10.3969/j.issn.1673-2065.2020.04.003

任洪波（1975－），男，河北枣强人，助理实验师；

孟令辉（1985－），男，河北武邑人，实验师。

O475

A

1673-2065(2020)04-0012-04

2020-03-31

（责任编校：李建明 英文校对：李玉玲）